鸽形扑翼机构设计及翅翼周围流场分析
2022-09-16李佩郭忠峰王赫莹
李佩,郭忠峰,王赫莹
(沈阳工业大学,辽宁省智能制造与工业机器人重点实验室,辽宁沈阳 110870)
0 前言
仿生扑翼飞行器是近年研究热点之一,它是基于鸟类和昆虫扑翼飞行特点研制的新型飞行器,通过扑翼产生气动力帮助飞行器前进和上升,在民用和军用领域都得到了广泛应用。扑翼运动系统是扑翼飞行器的关键,美国Caltech公司研制的MicroBat是一种通过模仿昆虫扑翼运动实现飞行的小型飞行器;中国台湾中华大学TSAI团队研究的微型扑翼飞行器以及哈尔滨工业大学刘聪设计的驱动机构都选用了单曲柄双摇杆机构,该机构存在一定的相位差,不能实现扑翼运动左右对称。目前应用较广泛的是双曲柄摇杆机构,中国民航大学苏汉平设计的仿鸟扑翼飞行器应用了双曲柄双摇杆机构;沈阳理工大学郭梦辉和合肥工业大学舒宁等人都应用双曲柄双摇杆机构设计了扑翼飞行器。随着计算流体力学(Computational Fluid Dynamics,CFD)的发展,越来越多的人将计算流体力学数值模拟计算应用于扑翼飞行的流场分析。
本文作者在现有研究基础之上,基于曲柄摇杆机构和二级差动原理优化设计出一种双曲柄摇杆机构,实现扑翼运动;然后采用CFD对扑翼飞行气动流场进行分析计算,通过Fluent数值分析的方法模拟翅翼扑动引起周围空气流场变化,得出翅翼周围流场的压力、速度、流动状态、气动升力、推力的变化规律。
1 扑翼机构设计与三维建模
1.1 设计要求及机构分析
选用双曲柄摇杆机构作为鸽形扑翼飞行器的驱动机构。驱动部分由两部分组成:一是以曲柄所在的齿轮盘作为动力源建立平面四杆机构,将齿轮的转动转化为四杆机构的摆动;二是连杆作为动力源连接旋转连杆来改变力的作用方向,将仿生扑翼飞行器的翅膀分为一级翼、二级翼,它们之间通过一体式二级连杆连接,从而达到差动控制一、二级翅翼的目的。
采用图解法对鸽形扑翼飞行器驱动机构进行设计,因扑翼上下扑动运动需要具备急回特性,如图1所示,曲柄沿顺时针方向转动到达位置,此时曲柄与传动杆共线,即扑动杆到达第一个极限位置,如图中所示位置;曲柄继续顺时针转动,同理当曲柄与传动杆再一次共线,到达第二个极限位置,如图中所示位置;如此反复循环运动。

图1 曲柄摇杆机构运动示意
1.2 扑翼机构优化设计
采用上述曲柄摇杆机构进行扑翼机构设计,两个曲柄摇杆机构左右对称布置、同步扑动,优化设计出具有最佳传动性能的扑翼运动机构。图2所示为曲柄摇杆机构解析图,其中:为极位夹角;为扑翼幅值。
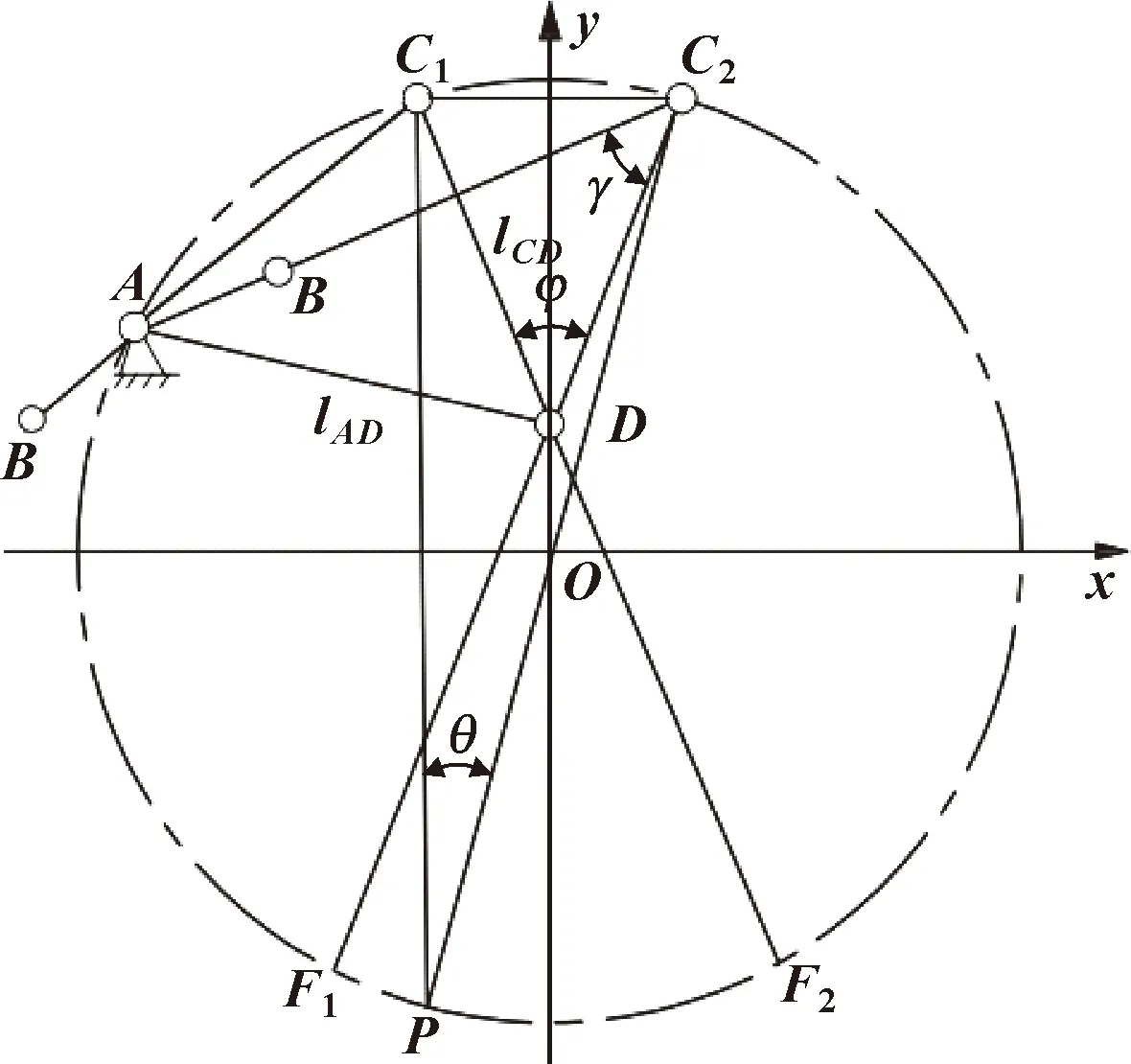
图2 曲柄摇杆机构解析图

当点位于位置时,机架取最小值1;当点位于位置时,由图知:
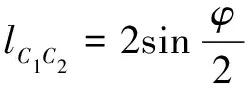
(1)

(2)
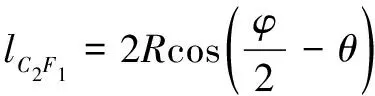
(3)
联立式(1)—(3)可得机架最大值为

(4)
则机架的取值范围:
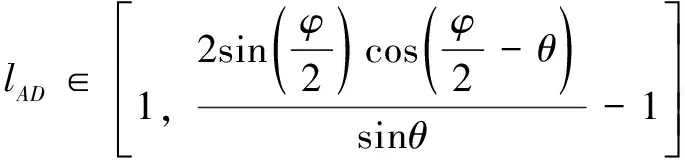
(5)
在扑动杆长度为1时,该机构属于I型曲柄摇杆机构,查找资料有如下结论:
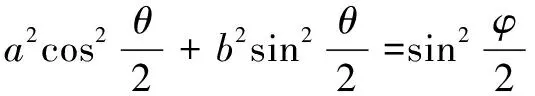
(6)
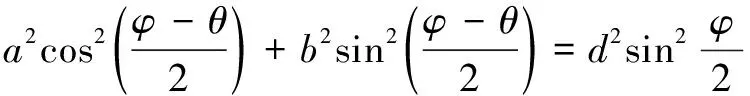
(7)
联立式(6)、(7)得:

(8)
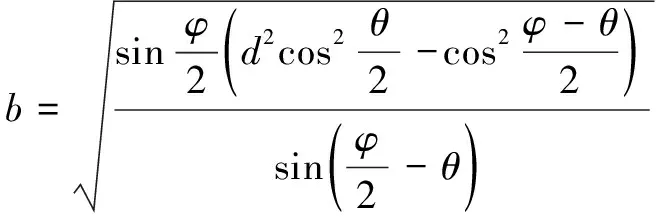
(9)

当曲柄延顺时针方向转到与机架共线的两个位置时,传动角出现最小值,根据几何关系有:

(10)
将各杆长表达式代入得:
=
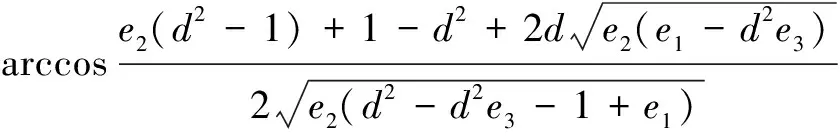
(11)
在给定扑翼扑动幅值、极位夹角的情况下,可得到机架长度的取值范围以及在此条件下对应的最小传动角的最大值和驱动机构其他单位杆长,将扑翼扑动设计参数=π/6、=π/12分别代入得:=0.150 4、=1.928 6、=0.021 8、1 cm<<2.471 4 cm。
将上述数值代入公式(11),再利用MATLAB求解上式的最优解,得到最小传动角与机架长度关系曲线如图3所示。

图3 最小传动角与机架长度关系曲线
根据上述分析计算,当机架位置最佳位置为=1.26 cm时,按照函数一一对应关系最小传动角取得最大值=0.23π,符合最小传动角大于许用值的要求。综合考虑扑翼机构总体空间大小,取摇杆=3 cm。按照图2几何关系,有:=1.20 cm、=3.08 cm、=3.78 cm。
1.3 扑翼机构三维建模
扑翼机构主要包括驱动机构和连杆机构。在驱动机构的设计中,将微型直驱电机与输入端齿轮固连,通过减速机构传递扭矩。连杆机构根据前面分析计算结果按照合理的尺寸建立对称的双曲柄摇杆机构模型,建模过程中要注意杆件和齿轮相对位置关系,这将直接影响机构传动的可靠性和运动的准确性。整体扑翼机构如图4所示。

图4 扑翼机构的结构
2 数值模拟计算前处理
2.1 数值模型的建立
参考文献[11]建立以恒定速度前飞的翅翼数值求解模型,将其纵截面简化为如图5所示的二维模型。图中,弦长=0.1 m;空气流速恒定,用表示;标况下取空气密度=1.28 kg/m,空气流动速度0.2 m/s,空气动力黏度=14.8×10m/s;翼型与来流水平方向保持恒定的仰角。

图5 简化的翅翼纵截面二维模型
在扑翼过程中,由于柔性和空气流场影响,翅翼会沿弦向发生变形。扑翼飞行在一个周期内翅翼扑动规律和翅缘变形特点为:当翅翼从最低点开始上扑时,由于柔性和空气阻力的作用,翅缘部位和翅根部位变形不同步,翅缘变形逐渐增大,翅翼扑动经过水平位置时翅缘的变形达到最大,然后开始逐渐减小,翅翼扑动到达最高点时翅缘变形达到最小。翅翼下扑过程中扑翼规律和翅缘变形与翅翼上扑变化恰好相反。
2.2 计算参数的描述
在整个扑翼飞行的气动特性研究过程中,升力和推力是最能表征气动原理的参数,常用升力系数和推力系数作为计算参数来描述。根据-方程解得升力系数和推力系数表达式如下:
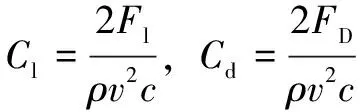
式中:、分别为扑翼升力系数、推力系数;、分别为升力、推力;为空气密度;为翅翼弦长。
2.3 流体域边界设置与网格划分
翅翼模型需要进行流体域边界设置,包括翅翼截面边界、流体入口和出口的边界条件。为模拟鸟类扑翼飞行时周围空气流场,应将翅翼周围空气流场边界放大到远大于翅翼模型尺寸的位置,在边界和翅翼实体壁之间形成一个流体域,然后在该流体域上进行网格划分。将翅翼模型置于如图6所示的边界条件流体域中,翅翼模型周围区域流场跟随翅翼一起运动,以获得较好的计算效果及较高的计算精度。

图6 边界条件及计算区域
CFD数值模拟结果的准确性和精度主要取决于网格划分和所采用的算法。为提高计算精度和稳定性,网格划分应符合流动区域的边界形状,并且容易引入边界条件,能较好地表征流场的物理参数。本文作者选用二阶三角形网格单元划分,然后对流体域网格进行动网格设置,网格质量较好,可以保证计算结果的准确性。划分后的网格如图7所示,总网格数为39 447,总单元数为78 999。
图7 流体域的网格划分
3 翅翼周围流场分析
在上述设置的扑翼参数和边界条件的基础上,将翅翼的柔性幅值设定为0.3。翅翼与周围流场的相对动压力云图和相对动压力变化曲线、湍动能云图和速度云图分别如图8、图9所示。

图8 翅翼压力云图及动压力变化曲线

图9 翅翼流场速度变化云图及湍动能云图
由图8可知:翅翼上部流场流动速度加大导致翅翼与周围流场产生相对动压力,整个翼面所受相对动压力为20~300 Pa,翅缘部位相对受压较大,这也要求翅翼结构设计时需采用柔性材料。由图9可以看出:变化较大的翅翼流场速度集中分布在翅翼附近,翅翼扑动引起流场速度变化最大至20.8 m/s;湍动能是表征湍流强度的物理量,湍动能云图表明由于翅翼周围空气流速变化较大导致在翅翼附近形成湍流旋涡,其湍动能最大达到15.2 J。以上分析表明扑翼飞行引起翅翼流场流动速度变化,进而导致空气流动状态由层流变为湍流,在翅翼附近形成巨大湍流旋涡,为扑翼飞行提供气动力,这也是扑翼飞行气动力的主要来源。升力系数、推力系数变化曲线如图10所示。
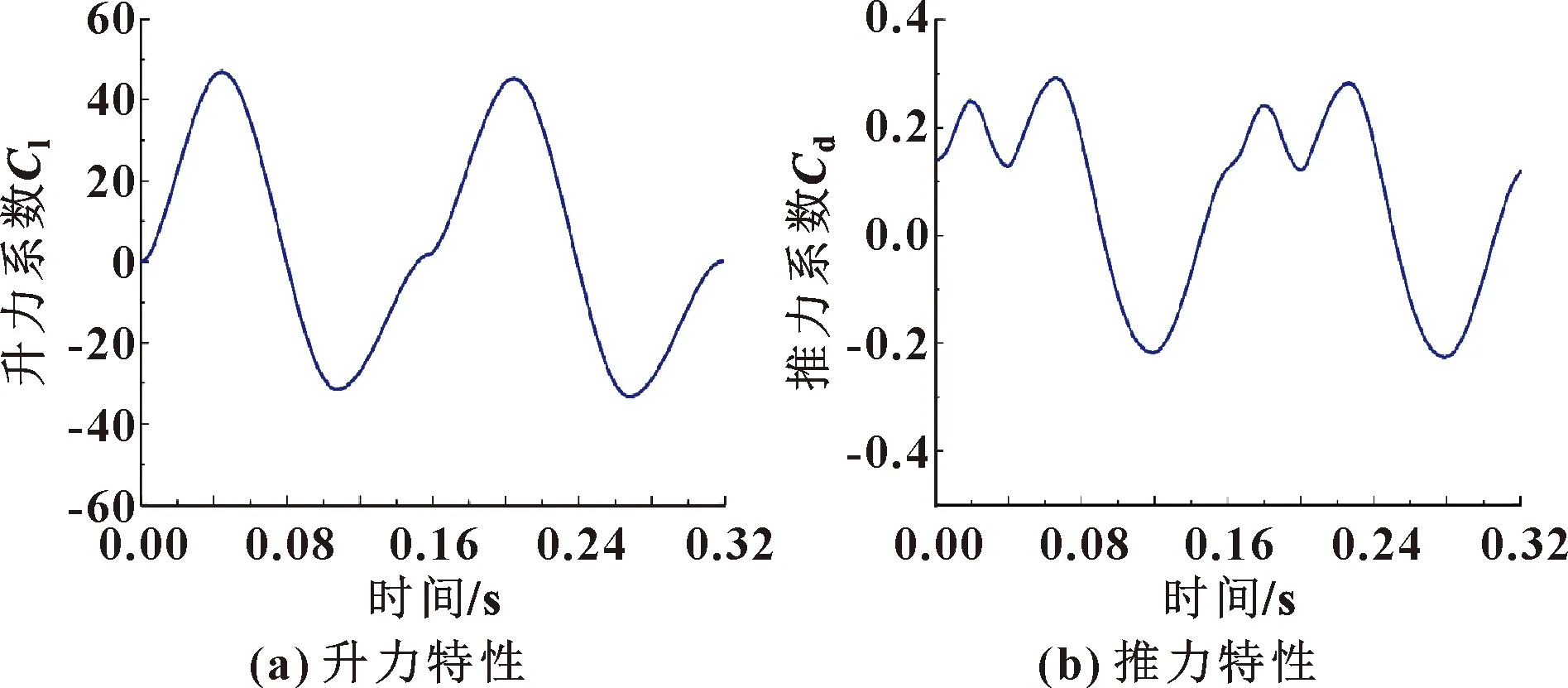
图10 翅翼升力、推力特性曲线
由图10可知:在扑翼飞行中由翅翼扑动产生的气动升力与理论扑翼运动模型的区别不大且呈一定周期性变化,翅翼上扑时升力系数逐渐增大,下扑时升力系数减小,整个周期平均升力系数为0.48,说明扑翼产生的升力大于上扑时空气阻力;翅翼扑动产生气动推力也呈一定周期性,当推力系数为负值时表现为阻力,平均推力系数为0.06,说明在翅翼扑动过程中产生的平均推力接近阻力,同时也说明该翅翼模型在空气流场中匀速前飞。
4 结论
本文作者优化设计了符合扑翼运动要求的曲柄摇杆机构,运用ANSYS Workbench Fluent软件对翅翼二维模型周围的空气流场进行分析计算,得出翅翼的压力云图、周围空气流场的速度云图和湍动能云图以及升力和推力系数在实际流场中的特性曲线。
结果表明:扑翼飞行引起翅翼流场流动速度发生变化,进而导致空气流动状态由层流变为湍流,在翅翼附近形成巨大湍流旋涡,为扑翼飞行提供气动力;在扑翼飞行中由翅翼扑动产生的气动升力和推力呈一定周期性变化,翅翼上扑时升力和推力逐渐增大,下扑时升力和推力减小至负值,表现为水平方向和竖直方向上的空气阻力,所以在整个运动周期中,翅翼既有升力产生,又有推力产生。
