浸润数学思想 折射智慧课堂
2022-06-11张利平
数学是教育事业中不可或缺的存在,“图形与几何”教学又是数学教学中的重要内容,小学生抽象思维和空间观念还不成熟,这导致在“图形与几何”模块知识点学习中非常困难,转化思想是一种常见的数学思想,不仅能够带领学生更好地解答数学“图形与几何”问题,同时还能够让学生提升抽象思维、空间想象能力等,因此,在“图形与几何”教学中,善于利用转化思想来教学,让学生学得轻松、学得有效,具有非常积极的现实意义。
下文首先对转化思想在“图形与几何”中应用的多种常见形式进行综合性分析,其包括切割法、倍比法、割补平移法、等量代换法、代数法等,详细结合例题进行说明。其次对转化思想巧妙渗透、传授给学生的策略进行分析,教师可以通过分发材料让学生实际模拟、多媒体技术直观呈现、一题多解等优秀方法将转化思想传输给学生,培养学生的抽象思维和空间想象能力,促使学生在数学领域越走越远。
一、转化思想在“图形与几何”中的应用
(一)转化思想的价值
数学是一门抽象学科,优秀的数学思想或理念随着数学的深入钻研应运而生,过去小学数学课程着重于教导学生数学知识,而新时代数学课程则着重于教导学生数学思想或理念,用简单的话来说,就是在帮助学生学到知识的前提下,帮助学生建立理性思维、逻辑能力、推理表达能力等。转化思想就是“图形与几何”知识点教学中的重要思想,将复杂的图形与几何问题转化为简单的问题,再进行解答,教学中的难题并不是有意刁难学生,而是要培养学生的空间想象能力和数学转化思想。
(二)转化思想的多种呈现
1.分割法
分割法是转化思想中最基础的理念,将较大的图形、较复杂的关系切割成简单的图形,让学生用学过的知识去解决。例题1:如下图1所示,两个边长为8厘米和5厘米的正方形搭在一起,求下图阴影面积。解答1:观察图形,阴影面积较大,如果按照原本正方形来分解,那么自然会有未知边长的阴影面积要计算,而如图1所示分割,将图形分割成三个三角形,左边三角形为1/2*5*8=20,上面三角形为1/2*5*(8-5)=7.5,右边三角形为1/2*5*5=12.5,最终加起来为38平方厘米。
2.切割平补法
对图形和几何进行切割,并通过平补来将不熟悉的图形转化为熟悉的图形,之后用相关知识去解答。例题2:如下图2所示,一个平行四边形被实线分割成三角形和梯形,梯形和三角形的面积相差为40平方厘米,三角形的高为8厘米,求梯形下底边长。解答2:简单分析:做下图2所示虚线,两边的正、倒三角形是相等的,那么梯形和三角形的面积差就是如图平行四边形的面积,又知道了高为8厘米,那么梯形下底边长就是40/8=5厘米。
3.倍比法
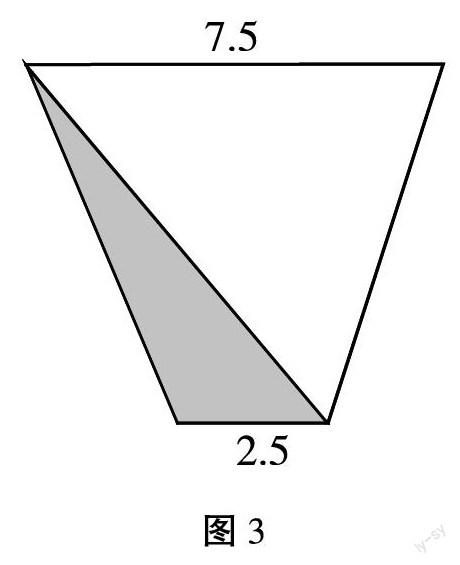
将具有倍数特征的图形用倍比法来进行解答,例题3:如下图3所示,已知阴影部分面积为25平方厘米,求整体梯形的面积。解答3:运用笨办法要先算出阴影三角形(梯形)的高,根据所有条件计算梯形面积,而运用倍比法,利用阴影部分与整体梯形的倍数关系,空白三角形面积为阴影三角形面积的三倍,整体梯形面积为阴影三角形面积的四倍,所以梯形面积为25*4=100平方厘米。
二、转化思想巧妙渗透、传授给学生的策略
(一)自主实践探究法
培养学生的自主学习能力,改变以往知识由教师灌输的教学方式,学生的知识获取是自己探索学习来的,而不是从教师口中听来的,对数学知识点的思考和理解會更加彻底,会更加深入地领会数学学习的魅力和乐趣。尤其是对转化思想来说,教师只给学生介绍方法是不行的,需要让学生进行实践探究,提升思想认知,才能让学生在心底有更好的理解。给学生准备几何图形的卡片或者模型,结合题型演练,让学生参考题型去实践演练,裁剪小纸片来折叠、平移等,加强理解,转化思想会在实践过程中渗透给学生。
(二)多媒体演示法
随着时代发展,多媒体与教育的整合已经越来越深入,善于利用多媒体,对一些抽象、空间的知识非常有帮助,多媒体内容更加丰富、有趣,呈现方式更加新颖、生动,有助于教学中开展各种活动,为学生创设各种情境,激发学生的思维潜能。在“图形与几何”学习中,大屏幕放映几何图形,将重点区域用不同颜色标注,做辅助线、做切割线、将图形切割平移等操作都会变得异常方便,也有利于学生加强对转化思想应用的理解,同时,多媒体展现的几何图形更加形象、直观,能激发学生的抽象思维和空间想象思维。
(三)一题多解
在渗透教学转化思想的时候,为了体现其实际应用,也可通过一题多解的方法培养学生思维的灵活性,将转化方法巧妙渗透、传授给学生。
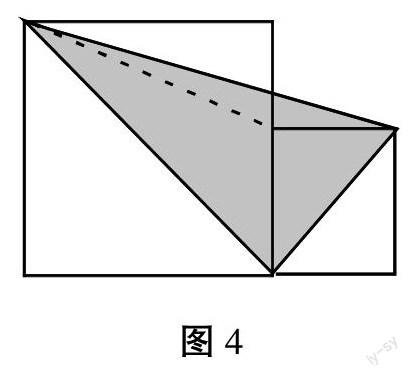
例题4:在例题1的基础上进行分析,如下图4所示,回顾例题1:两个边长为8厘米和5厘米的正方形搭在一起,求下图阴影面积。
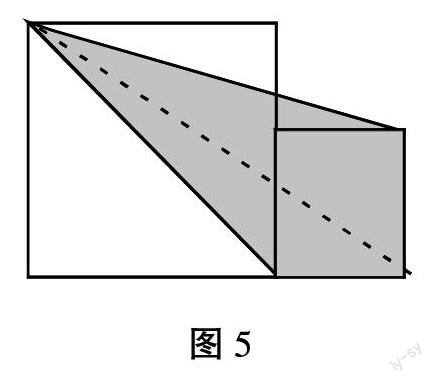
解答4:我们观察例题1,第一种解答方法是将图形分割成三个三角形,分别计算三个三角形的面积,最终相加起来,那么如下图5所示,将阴影部分扩充,只需要分解成两个三角形即可,而后可以求得扩充的图形面积,最终再减去扩充图形的面积,就能得出原阴影图形面积,不失为一种独到解法。教师巧妙利用一题多解,势必能优化学生的思维路径,提升学生思维的灵敏度,提升“图形与几何”的解题能力。
三、结语
综合来说,“图形与几何”教学是小学数学教学中的难点,巧用转化思想,能让几何图形知识解决起来更加方便,因此,教师要将转化思想的精髓讲授给学生,既能加强“图形与几何”知识点学习,又能培养学生的抽象思维能力。本文对在“图形与几何”中常见的转化思想进行了分析、阐述,包括切割法、倍比法、割补平移法、等量代换法、代数法等,并对每一道转化配合例题进行了讲解,用优秀教学模式和方法潜移默化地培养学生完善的数学思维和数学素养,将促使学生在数学领域越走越远。相应的,教师可以通过让学生自主实践、多媒体加教学培养想象力、一题多解提升思维灵活度等多种策略来将转化思想巧妙渗透、传授给学生。
作者简介:张利平(1970—),男,汉族,甘肃兰州人,本科,一级教师,就职于甘肃省兰州市榆中县建亭小学,研究方向:小学数学。
