考虑残值变化和消费者低碳偏好的生产定价与销售激励机制
2022-06-11陈克贵王新宇
陈克贵, 王新宇, 黄 敏, 任 亮
(1.中国矿业大学 经济管理学院,江苏 徐州 221116; 2.东北大学 信息科学与工程学院,辽宁 沈阳 110819; 3.武汉科技大学 管理学院,湖北 武汉 430081)
0 引言
随着经济全球化的发展和社会分工的日益细化,制造商通常雇用销售商销售产品,并根据相应的市场销量激励或补偿销售商。比如电子行业中,销售商通过与顾客直接交流传送产品的个性化信息,进而销售同一厂家生产电子产品。制造商希望多销售产品,但销量的增加将导致更高的销售成本,对于制造商来说,关键的问题是如何处理好与销售商间的利益冲突。另外,价格也是影响厂家、销售商、消费者等利益相关者及市场前景的重要因素,制定合理的价格是维护制造商利益、调动销售商积极性的关键。因此,如何设计合理的销售激励机制并制定合理的价格对制造商来说至关重要[1~4]。企业的生产定价决策及对销售商的销售激励机制设计问题,已有学者从不同角度做了研究。Oh和Pal等[5,6]针对供应链的最优生产和价格联合决策问题展开研究,但都基于对称信息的视角。陈剑等[1]在不对称信息下研究了制造商对销售商的最优销售激励契约设计问题及最优生产定价联合决策,并分析信息不对称对制造商和销售商参与双方决策和收益的影响;Dai等[7]在销售商风险规避度不对称下探讨制造商如何设计销售激励合同及存货管理,并得到最优激励契约及库存决策;Lee等[8]在不对称信息下多销售商竞争时设计销售激励合同并探究生产定价决策问题。陈克贵等[9]探讨了制造商面对过度自信销售商时的销售激励契约设计及生产定价联合决策问题,并分析过度自信行为对制造商和销售商双方策略和收益的影响。
在低碳经济背景下,越来越多的消费者有低碳偏好行为,数据调查显示,在美国有67%的消费者在购买商品时考虑低碳因素的重要性,甚至愿意为低碳商品支付额外的碳减排成本,低碳商品销量高于非低碳商品,由此可见消费者的低碳偏好会影响商品的市场需求和供应链成员的运作策略[10~12],面对消费者不断提高的低碳意识,企业该如何决策单位商品的碳减排量、生产定价决策及对销售商的销售激励契约设计具有重要的现实意义。供应链碳减排问题受到许多学者的关注,Benjaafar等[13]在供应链中提及了碳排放问题,分析了碳排放对供应链各参与主体决策的影响,并探讨了碳排放与供应链运作的关系。Hua等[14]的研究结果表明碳限额和碳交易价格都将影响零售商的订货决策。从制造商运作角度出发,Dong等[15]在限额与交易政策下分析制造商的减排投资决策和零售商的订货策略问题。Lee等[16]分析比较证实,相对于下游企业,上游企业参与碳减排更有效。Du[10]和Yalabik[17]将消费者低碳偏好引入到市场需求函数中,进而分析碳减排量与供应链运作的关系。王芹鹏等[18]探讨了消费者有低碳偏好时的契约设计,并分析制造商的最优减排和销售商的最优订货决策,本文也正是假设了市场需求取决于消费者的低碳偏好。尽管一些研究将消费者的低碳偏好考虑在内,但都假设残值是常数的而没有考虑残值依赖于剩余库存的情况。
考虑不对称信息下产品的生产、定价与销售激励决策是近些年企业界和学术界关注的热点。然而,从现有的研究来看,除了Aviv等[19]在相机定价问题中考虑了剩余库存量的影响之外,当前的研究通常都假设残值是固定值。然而现实生活中更多的情况是,销售商在销售季末会根据产品剩余数量做打折处理,剩的越多,折扣就越大。季末折扣价(即残值)随剩余库存量变化下,制造商该如何定价与生产决策,以便获取更大的利润?是值得进一步关注的问题[19,20]。王夏阳等[21]在考虑残值变化和顾客异质性下,分析顾客异质性如何影响零售商定价与库存决策,但都是基于对称信息的假设下,且没考虑对零售商的销售激励和碳减排问题。本文将考虑残变化下制造商的定价、生产、碳减排决策问题,即本文还将在考虑消费者低碳偏好时进一步探讨残值变化对双方决策和收益的影响。
本文探讨制造商面对产品残值变化和消费者低碳偏好下的销售激励契约设计及生产、定价和碳减排联合决策问题,进而分析碳减排成本和残值变化率对双方策略和收益的影响,并做相应的对比分析。研究结果表明,随着残值变化率的增加,只有制造商的期望收益和订货量将降低,但碳减排成本的增加将导致销售商的销售努力程度,制造商的最优减排量、最优生产和价格决策及其期望利润等都会降低,最后结合算例验证相关结论。
1 问题描述与模型假设
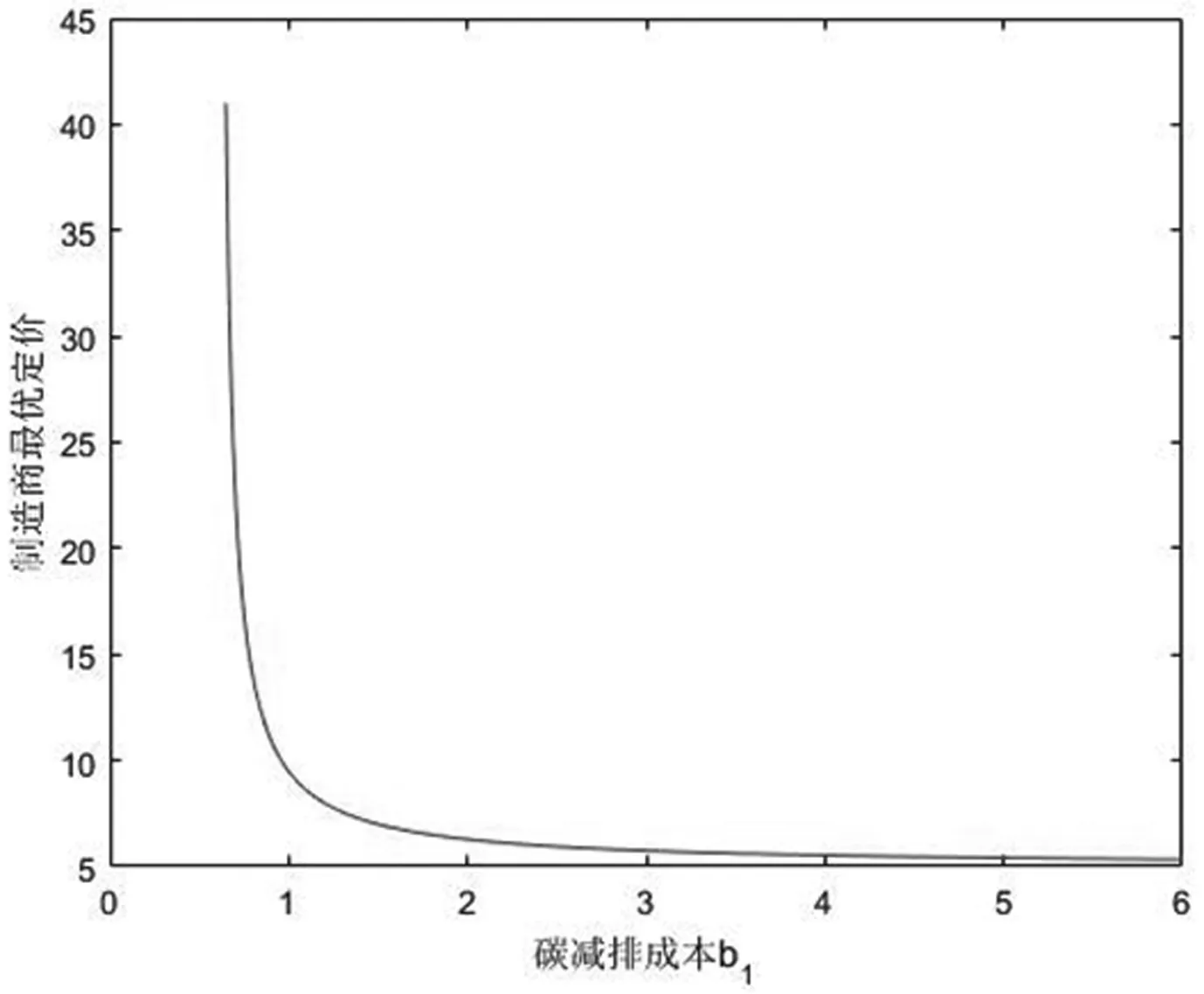
考虑制造商委托销售商销售产品并支付销售商相应的报酬,在产品销售前,制造商制定价格p、产品的碳减排量e1、生产量Q以对销售商设计销售激励契约,销售商选择销售努力程度e2。假设单位产品的生产成本为c,供给大于需求时,单位剩余产品的残值为s′,s′<0表示剩余产品需处理成本,供给小于需求时,加急生产的单位成本为c′,且s′ 将碳减排量引入市场需求函数中,假设市场需求受制造商的减排量e1,销售商的销售努力e2、销售价格p、基本市场规模a及随机因素θ等参数的影响,需求反应函数为[22~25] X=a-bp+e1+e2+θ (1) 其中b>0为价格敏感系数,且a-bc>0(销售价p接近c,努力很小时,保证非负期望需求),θ服从均值为零、方差为σ2的正态分布,其概率密度函数和分布函数分别为f(.)和F(.)。 制造商根据销售量X向销售商提供线性契约s(X)=α+βX,记为(α,β),其中α为与销量无关的固定支付,β≥0为制造商的销售激励系数[1,6,7]。 以往的研究都假设清仓期的残值s是常数。实际中当产品在错过销售旺季后降价出售时,商家通常按清仓期的库存调整价格。一般当剩余库存量越大时,商家都会把价格(即残值)调得越低[19~21]。假设清仓期残值s′依赖于期末库存Max(Q-X,0),并满足s′=s-γ(Q-X)*,其中残值变化率γ是常数。此时残值s′是随机变量,且依赖于随市场需求X和生产量Q。 假设制造商风险中性,结合上述假设,制造商的净收益为 πM=pX-cQ+s′(Q-X)+-c′(X-Q)+-s(X)-C1(e1) =pX-cQ+[s-γ(Q-X)+](Q-X)+- c′(X-Q)+-s(X)-C1(e1) =pX-cQ+s(Q-X)+-c′(X-Q)+- γ((Q-X)+)2-s(X)-C1(e1) (2) 其中x+=max(x,0),销售商的净收益为 πs=s(X)-C2(e2) (3) 假设销售商风险规避,其效用函数为Us=-e-ρπS,ρ>0为风险规避度,销售商的保留效用为-U0,则相应确定性等值为π=-lnU0/ρ。当激励契约(α,β)给销售商带来的期望效用大于其保留效用时,销售商才接受契约,即E[-e-ρπS]≥-U0成立,接受契约的销售商确定性等值满足 CES=α+β(a-bp+e1+e2)- (4) 式(4)为销售商的个人理性约束IR(individual rationality constraint)。 上述假设为制造商和销售商参与双方的共同知识。为了方便,将销售努力成本系数、风险规避度与需求方差的积A=b2ρσ2称为传统因子;E(.)为期望算子;下标M和S分别表示制造商和销售商,下标C表示残值为常数(Constant);上角标*表示各变量取最优值。 由上节假设及式(2)可知,风险中性制造商的期望效用为 E(πM)=E[pX-cQ+s(Q-X)+-c′(X-Q)+- γ((Q-X)+)2-s(X)-C1(e1)] (5) (6) γ((Q-X)+)2-s(X)-C1(e1)] (7) s.t. (IR)CES=α+β(a-b+e1+e2)- (8) 上述的IR约束为销售商的个人理性约束,式(8)的IC约束为销售商的激励相容约束。 销售商的最优努力程度可由式(8)的IC约束的一阶条件得到: (9) 求解上述模型,可得下述定理中制造商和销售商双方的最优策略及最优契约配置。 (10) 最优生产量Q*满足关系: (11) 相应地,固定支付为 (12) 制造商的最优期望收益为 π+π(β*) (13) 其中 π(β*)=(c′-c)(Q*-m(β*))- [2γ(Q*-m(β*))+c′-s]× (14) (15) 由上述定理的结论可知,制造商可通过对自身的碳减排量、定价及激励契约联合决策来引导销售商付出最优的销售努力水平,以实现其最大化目标。 由上述定理的结论可得下述推论1。 推论1当残值变化率为γ时,最优生产量Q*满足关系: (16) 其中,T唯一存在并由式(17)确定: (17) 或者 (18) 并且 π(β*)=(c′-c)T-[2γT+c′-s]× (19) 或者 π(β*)=(c′-c)T-γF(T)(T2+σ2)- (c′-c)TF(T) (20) 由推论1的式(17)可知,T仅与残值变化率γ,加急生产成本c′,初始残值s和生产成本c有关,与销售成本b及其制造商的碳减排成本b1等参数都无关。 当残值不变,即γ=0时,由定理和推论1的结论可得下述推论2。 (21) (22) 在残值变化及消费者低碳偏好下,上述最优契约有怎样的特征?残值变化率和碳减排成本对双方的决策和收益有什么影响?本节分析上述定理和推理中的均衡结果,有以下结论: 结论1在残值变化和消费者低碳偏好下,残值变化率γ只影响制造商的收益E*(πM)和生产量Q*,不影响制造商的定价、销售契约及零售商的决策和收益,和制造商的碳减排成本和减排量无关,且残值变化率γ越大,制造商的最优期望收益E*(πM)和生产量Q*越低。 由定理的式(11)结合隐函数求导得: 由定理中的式(13)可知,E*(πM)中γ仅影响π(β*),且由式(14)并结合隐函数求导得: Q*-m(β*)等于定值T,由式(10)决定(推论1)。 类似地,结合式(16)、式(17)和式(19)可由隐函数求导可得,加急成本c′越高,初始残值s越大,制造商的期望收益E*(πM)和生产量Q*就越高,与带缺货惩罚报童模型的结论一致[1]。 根据式(11)中加急生产成本c′与生产量Q*的关系: 结合隐函数求导可知,生产量Q*与加急生产成本c′的关系为: 通过分析最优生产量Q*关于残值变化率γ和加急成本c′的关系可知,当加急成本c′相对较小且残值变化率γ较大时,企业可能不会提前生产过多产品,接近于按需生产;反之当加急成本c′较大且残值变化率γ较小时,企业可能提前生产相对较多的产品。 结论2残值变化和消费者低碳偏好下的生产量和制造商的期望收益都要低于残值不变的情形,即 (23) 结论2表明,残值变化使得制造商在制定生产量上有所保留,并导致制造商收益的下降。 结论3说明,制造商的期望收益、设定的契约参数与碳减排成本负相关。碳减排成本较低时,制造商可通过加大减排量并提高价格来获取更高的收益。市场期望需求D*并没有随着价格的升高而减少,这也说明消费者愿意为其低碳偏好付出额外的低碳成本。 图3 碳减排成本b1对最优定价p*的影响 图4 碳减排成本b1和残值变化率γ对最优生产量Q*的影响 图5 碳减排成本b1和残值变化率γ对制造商最优期望收益E*(πM)的影响 从图1~图5可知,销售商的销售努力程度、制造商的碳减排努力程度、最优定价、生产量及制造商的收益都随着碳减排成本的增大而减少,与结论3一致;图4和图5还显示,制造商的最优生产量和收益还关于残值变化率递减,与结论1的一致。 以制造商雇佣销售商销售产品为背景,分析消费者低碳偏好和残值依赖于剩余库存时,制造商如何进行碳减排、生产、定价决策及设计销售契约来激励销售商积极参与。首先分析残值变化和消费者低碳偏好下双方的决策问题并建立模型,求解模型得到制造商的最优定价、碳减排量、生产量、最优激励契约、销售商的最优努力和制造商的收益。然后分析比较双方的最优决策和收益以及关于碳减排成本和残值变化率的关系。结果表明:当残值变化率相同时,提高碳减排成本将导致制造商收益和碳减排量的下降,销售商的销售努力程度,制造商的最优定价和生产量也将下降;但残值变化率的增加只导致制造商的收益和最优生产量的下降。最后给出了算例分析碳减排成本和残值变化率对制造商和销售商双方决策和收益的影响。 本文仅考虑消费者低碳偏好一致的情况,未来将进一步考虑消费者低碳偏好异质性及不同领导权下的碳减排决策问题[21,26]。此外,本文考虑线性契约及残值与剩余库存量呈线性变化的情形,若进一步考虑其他形式的激励契约,如非线性契约或阀值契约[4,8],及残值关于清仓库存量呈非线性变化,则双方的决策和收益将会发生怎样的变化;本文的研究是基于完全理性的假设,忽略了供应链成员的行为因素[9,27]。因此,未来将考虑成员的行为倾向并涉及非线性激励契约及残值关于清仓库存量呈非线性变化的情况,使效用函数的刻画更接近现实。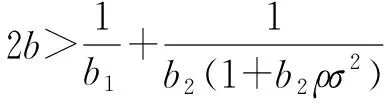

2 残值变化和低碳偏好下的模型
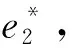
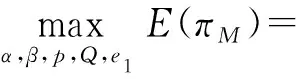

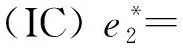

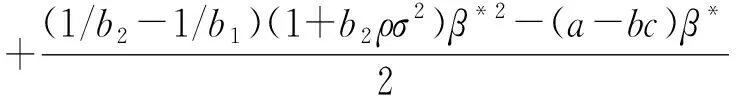
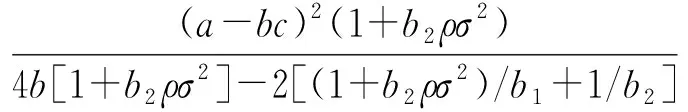
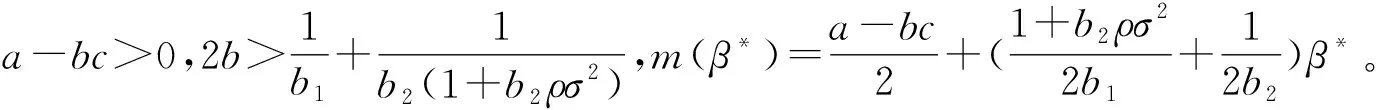
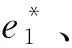
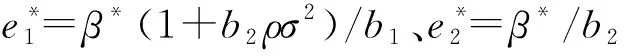
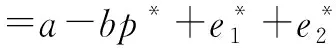
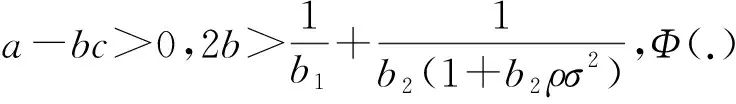

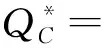
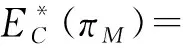

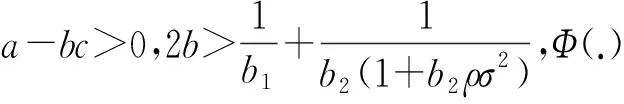
3 模型结果分析
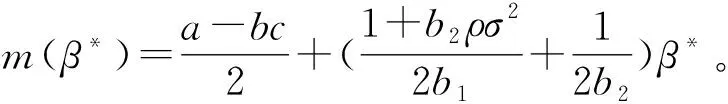
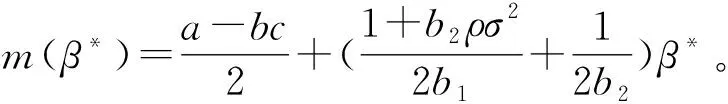


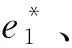
4 数值算例分析

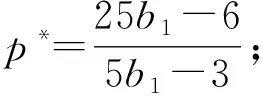

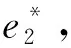

5 结语
