深层页岩气压裂井套管应力影响因素分析*

林 魂 宋西翔 孙新毅 杨 兵

(重庆科技学院安全工程学院)

0 引 言

水平井+分段多级压裂技术为目前开发页岩气资源的主要手段[1-3]。在实际压裂施工过程中，套管变形问题尤为突出，影响着页岩气井的正常生产[4]。目前一些学者对此类问题做了一定研究。水平段井筒温度变化会降低套管抗压强度[5-7]。大规模水力压裂会诱发断层滑动，造成套管变形，即使是调整水泥环弹性模量、厚度以及套管壁厚等参数都很难保证套管安全[8-10]。套管变形是多因素综合作用的结果，在温压耦合条件下，固井质量差会增加套管应力，加剧套管失效风险[11-13]。

与中浅层不同，深层页岩气储层具有高温高压、层理裂隙分布复杂以及水平两向地应力差大的特点。为了获得更好的增产效果，往往需要地面泵车提供超高的泵注压力。这使得水平段套管处于较为复杂的力学环境中，套管失效风险增大[14-17]。近年来，众多学者开始借助有限元软件对套管变形机理进行研究，但大多数研究对象主要为中浅层页岩气储层，专门针对深层页岩气储层套管变形的数值模拟研究还较少。鉴于此，本文借助有限元分析软件ANSYS，通过构建水平段套管-水泥环-地层组合体模型，研究了压裂过程中温-压耦合作用、断层滑移及“密簇”压裂对深层页岩气井水平段套管应力的影响。研究结果可为保障深层页岩气井水平段套管的完整性提供一定的参考。

1 模型建立

1.1 基本假设

固井后，水泥浆凝固，形成固态水泥环，将套管和地层紧紧耦合在一起。水平井压裂如图1所示。选取套管-水泥环-地层力学系统为研究对象，构建深层页岩气井水平段套管-水泥环-地层组合体模型，如图2所示。为简化模型计算，做出如下基本假设：①套管-水泥环-地层之间紧密结合，各交界面之间接触良好；②套管、水泥环和井眼为理想圆柱形；③套管、水泥环和地层均为理想弹塑性体；④不考虑温度变化对材料属性的影响。

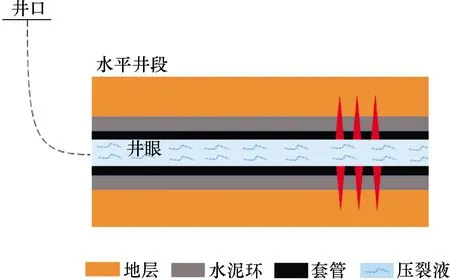
图1 水平井压裂示意图Fig.1 Schematic diagram of horizontal fracturing

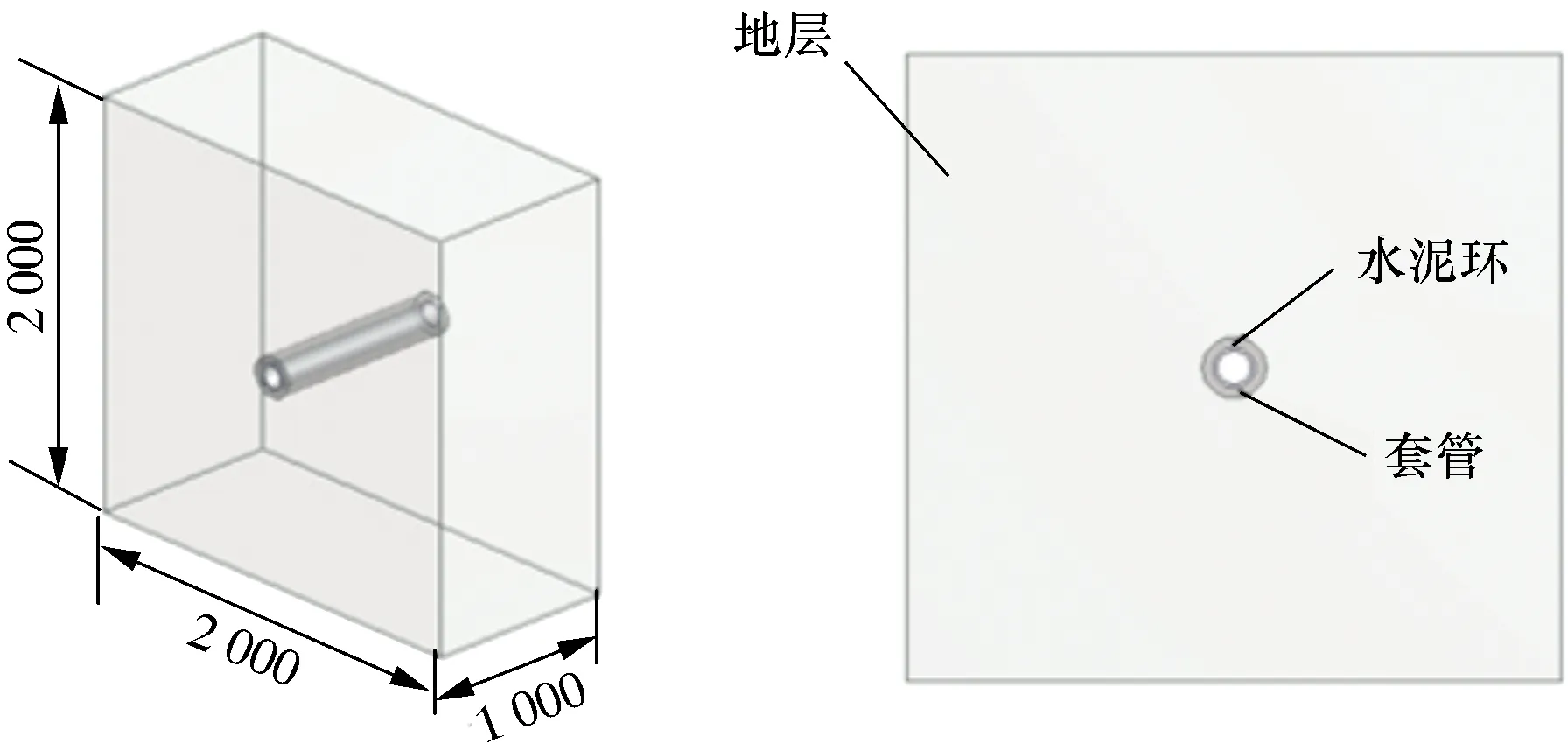
图2 套管-水泥环-地层模型Fig.2 Casing-cement sheath-formation model

1.2 模型尺寸

根据圣维南原理，取地层平面尺寸为井径尺寸的 5倍以上，以消除边界效应对套管受力的影响。具体尺寸参数如下：模型尺寸为2 000 mm×2 000 mm×1 000 mm，水泥环外径为216 mm，套管外径为140 mm，套管内径为115 mm。

1.3 材料参数

模型中，地层材料参数以川南地区威荣区块3 850 m深处页岩气储层的地质力学特性为参考[18]。取该区块地层弹性模量范围的平均值27.75 GPa作为材料参数设置,其密度为2 800 kg/m3，泊松比为0.237。为满足深层固井质量要求，水泥环的弹性模量设置为15 GPa，密度为1 950 kg/m3，泊松比为0.200。套管材料选取P110钢级，其弹性模量为210 GPa，密度为7 850 kg/m3，泊松比为0.300。

1.4 网格划分

对建立的几何模型进行有限元网格划分时，对模型面采用映射控制和局部加密的方法，网格单元类型设置为六面体。网格划分结果得到节点数1 291 467个，网格数243 300个，如图3所示。

图3 网格划分结果Fig.3 Mesh division

1.5 边界条件

根据川南地区威荣区块所测到的3 850 m深处的地应力场数据，取垂向地应力和最大水平地应力范围的平均值，即垂向地应力σ1=91.85 MPa，最大水平地应力为σ2=99.85 MPa。威荣深层页岩气井施工压力的平均值为82.50 MPa，则可以得到压裂时套管内壁压力σ3=140.98 MPa。模型边界条件如图4所示。分别在P1P2边和P2P3边施加垂向地应力σ1和最大水平地应力σ2，在套管内壁施加内压载荷σ3，分别在P1P4边和P4P3边施加全约束。

图4 模型边界条件图Fig.4 Boundary conditions of model

2 温-压耦合作用对套管应力的影响

2.1 温-压耦合模型

深层页岩气储层具有井底温度高，地层压力大的特点。在压裂过程中，高压低温的压裂液大量注入会导致水平段套管处于复杂的力学环境中，加剧套管损坏风险。因此，井底温压变化对套管应力具有重要影响。假设套管-水泥环-地层组合体之间传热方式为瞬态传热，根据热传导及弹塑性力学相关理论，该问题简化为平面热传导和应变问题。截取套管-水泥环-地层模型的中间横截面进行研究，具体模型材料热力学参数如表1所示。

表1 模型材料热力学参数Table 1 Material thermodynamic parameters of model

从压裂开始到泵注压力达到稳定值期间，大量压裂液进入水平井筒，并与套管内壁直接接触产生热交换，内壁温度迅速下降而压力迅速上升，水平井筒内的温度场和压力场均随时间而动态变化。本研究中，模型参数设置地层初始温度120 ℃，压裂液温度参考地面温度而设置为22 ℃，持续注液3 600 s。井筒内初始压力为静液柱压力(58.48 MPa)，注液开始后逐渐上升至施工泵压和静液柱压力之和(140.98 MPa)，并在之后达到稳定。

2.2 计算结果分析

图5为压裂过程中温-压耦合作用下套管内壁瞬态应力变化曲线。由图5可知：在泵压上升阶段，套管内壁最大等效应力呈现出先快速下降后快速上升的趋势，当达到泵压稳定阶段后，套管内壁最大等效应力也达到平稳。这是由于压裂初始阶段套管内部受较小的静液柱压力，外部受较大的深层地应力，导致套管内外受力不均而产生较大等效应力；当压裂开始后，套管内部泵压开始升高并与外部地应力逐渐达到平衡，此时套管受力更加均匀，产生的最大等效应力也会减小，并在710 s左右时达到最小值357.05 MPa；当套管内部泵压持续升高并超过外部地应力时，套管再次进入受力不均阶段，并在1 800 s左右时达到最大值589.59 MPa。

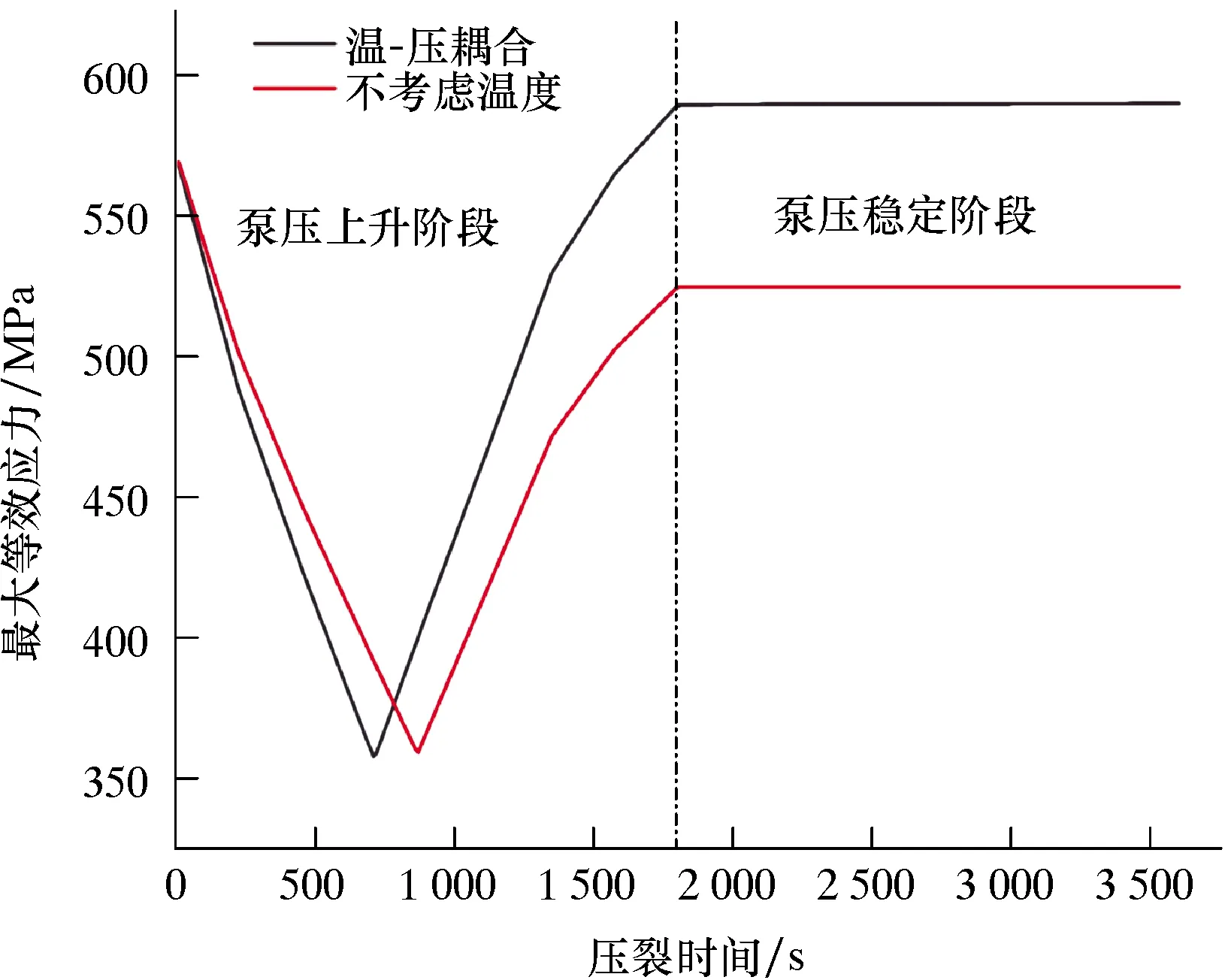
图5 温-压耦合作用下套管内壁瞬态应力变化曲线Fig.5 Transient stress on inner wall of casing under temperature-pressure coupling

当不考虑温度作用时，套管应力仅受泵压影响，当考虑温-压耦合作用时，套管应力受温度变化和泵压双重影响。图5反映了温-压耦合作用显著提高套管最大等效应力，相较于不考虑温度时，在泵压稳定阶段套管应力提升了65.33 MPa，这是随着压裂的进行，井筒内温度迅速降低而热应力迅速增大导致的。但在泵压上升阶段的790 s之前，温-压耦合作用产生的最大等效应力值略低于不考虑温度作用。这是由于在此时间段内，低温的压裂液大量进入井筒后与高温的套管内壁接触并进行热传导，在径向界面中产生较大的温度梯度，套管所受热应力迅速增大[19]，在与井筒内泵压耦合后使套管内壁应力大幅提升，减少了非均匀地应力的影响，降低了套管应力分布的不均匀差异。

随着页岩气储层埋深的增加，地温梯度增大，水平段井筒温差也会变大，当地层温度为120 ℃，压裂液温度为20 ℃时，温度降幅可达100 ℃。为进一步探究温差变化与套管应力的关系，选取泵压稳定阶段的不同泵注压力和井底温度进行研究，结果如图6所示。由图6可知，随着井口泵压的升高，套管内壁最大等效应力也呈逐渐上升趋势，并且井筒内温差越大，套管所受最大等效应力越大。模拟结果显示在相同泵注压力下，井筒温度每下降10 ℃，套管最大等效应力会增加8 MPa左右。

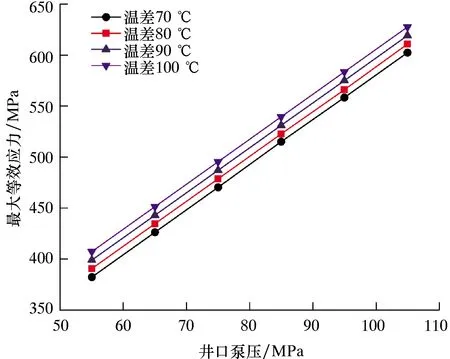
图6 温度和泵压对套管应力的影响Fig.6 Influence of temperature and pump pressure on casing stress

3 断层滑移对套管应力的影响

3.1 断层滑移模型

深层页岩气储层地应力更高，地层层序较多，天然断层和裂隙分布复杂。长时间大排量的高压注入压裂液会诱发断层活化滑动，使套管受到剪切而变形，这是导致深层页岩气井水平段附近套管严重损坏的主要因素。为研究在深层地应力状态下断层滑动距离对套管受力状况的影响，本文在前述套管-水泥环-地层模型的基础上建立了水平段断层滑移模型，如图7所示。

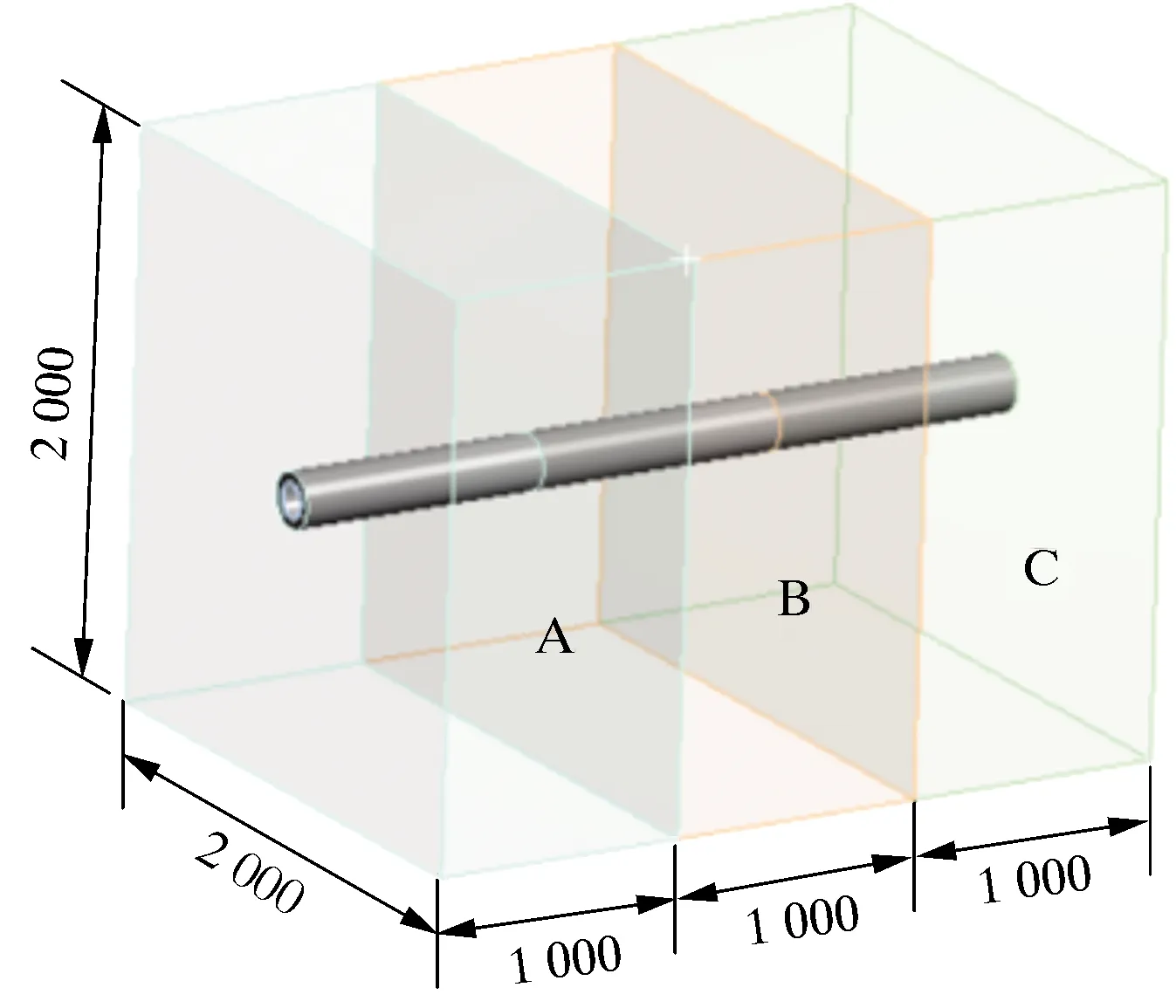
图7 断层滑移模型Fig.7 Fault slip model

断层滑移模型尺寸为2 000 mm×2 000 mm×3 000 mm。对模型施加原始地应力场载荷和套管内压载荷。将地层划分为A、B、C 3个尺寸大小相同的部分，各部分间采用摩擦接触，摩擦因数为0.6。假定B地层产生0～5 mm的滑动，滑动距离通过在断层面处施加位移约束来实现，以此模拟压裂过程中天然断层滑移。

3.2 计算结果分析

图8反映了在深层地应力作用下，断层滑移距离l对套管应力和变形的影响。从图8a可以看出：随着滑移距离的增加，套管内壁的最大等效应力呈不断上升趋势；当断层滑移距离超过3 mm后，套管在断层界面处开始受到明显的剪切应力；当滑移距离达到5 mm后，套管内壁最大等效应力达到最大值1 430 MPa。从图8b可以看出：套管变形量随滑移距离的增加而不断增大，二者几乎呈线性增长关系；当滑移距离为1 mm时，套管产生了1.4 mm的最大变形量；当滑移距离为5 mm时，套管产生了4.7 mm的最大变形量。

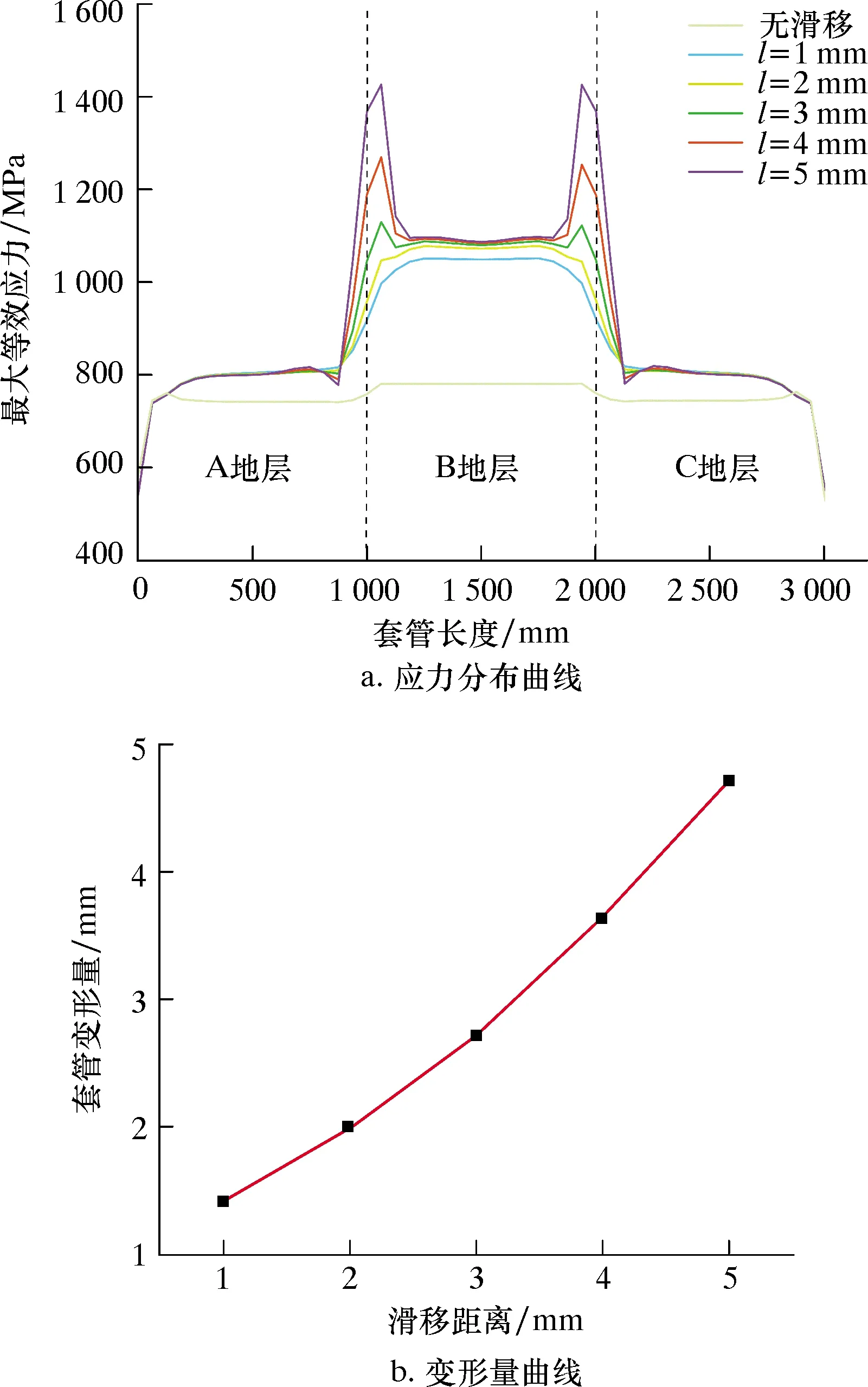
图8 不同滑移距离下套管应力和变形量曲线Fig.8 Casing stress and deformation with different slip distances

4 “密簇”压裂对套管应力的影响

4.1 “密簇”压裂模型

深层页岩气储层由于水平地应力差大，不利于形成复杂网缝，需要大排量大砂量的压裂液注入，因此常规的射孔方式已不适用于深层页岩气储层压裂造缝需要。当前多采用大孔径、短簇距的方法来提高深层页岩气井的压裂效果[20]。本文根据深层页岩气井水平井分段压裂实际工况，基于套管-水泥环-地层模型，建立单段长55.2 m，宽2.0 m，厚2.0 m的单段“密簇”模型，如图9所示。

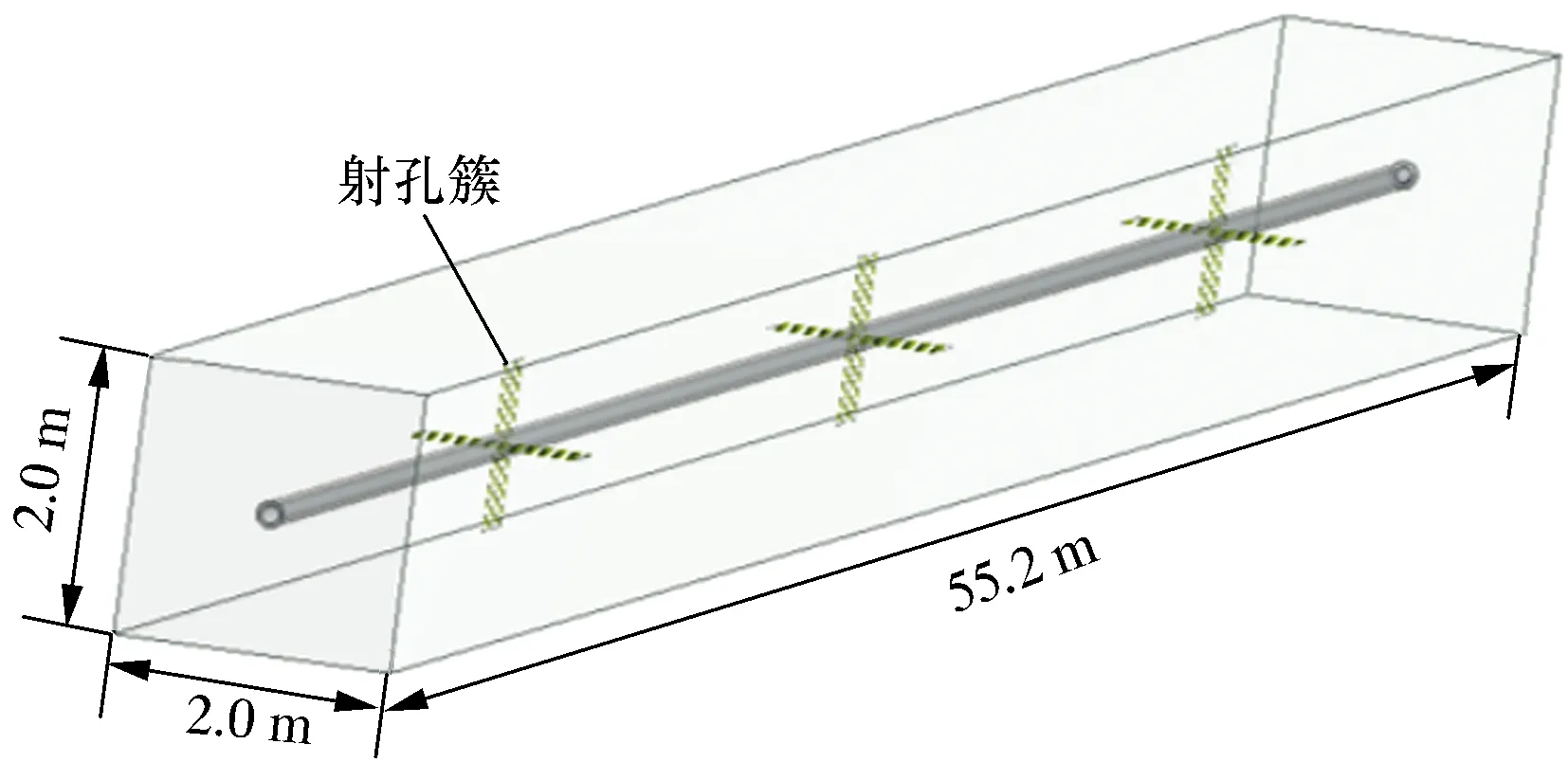
图9 单段“密簇”模型Fig.9 A segment of multi-cluster model

模型中射孔孔径为10.5 mm，相位角为90°，单簇长度为1 m，孔密为16孔/m。孔眼均为体积大小相等的圆柱体，且与井眼垂直。为了研究“密簇”对套管应力分布的影响，分别设置3、4、5、6、7和8共6组不同的射孔簇数值，簇间距分别为16 475、10 374、8 375、7 635、6 685和5 410 mm。

4.2 计算结果分析

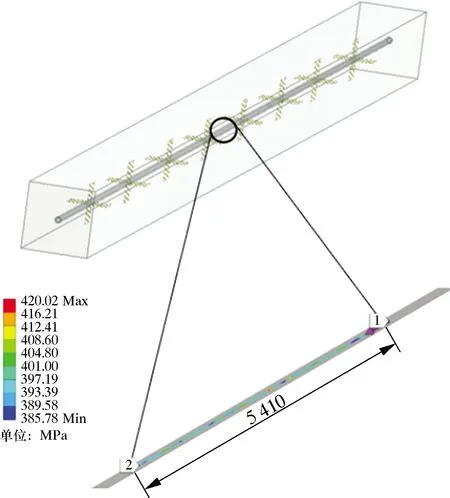
图10 两簇之间套管内壁等效应力云图Fig.10 Cloud chart of equivalent stress on inner wall of casing between two clusters

截取模型局部两射孔簇之间的套管内壁应力路径进行研究。图10反映了簇间距为5 410 mm(即簇数为8)时套管内壁等效应力，此时单段簇数最密集，簇间最大等效应力达到420.02 MPa。为研究“密簇”压裂对套管应力的影响规律，选取不同的簇间距为横坐标，套管内壁最大等效应力为纵坐标，绘制不同簇间距下最大等效应力曲线，如图11所示。当单段射孔8簇，簇间距离为5 410 mm时，套管内壁最大等效应力达到最大值420.02 MPa；当单段射孔3簇，簇间距离为16 475 mm时，套管内壁最大等效应力降为383.41 MPa，下降幅度约为9.5%。这说明深层页岩气分段压裂工艺中，“密簇”压裂会对套管应力产生较为明显的影响，簇间距离越小，套管所受应力越大。

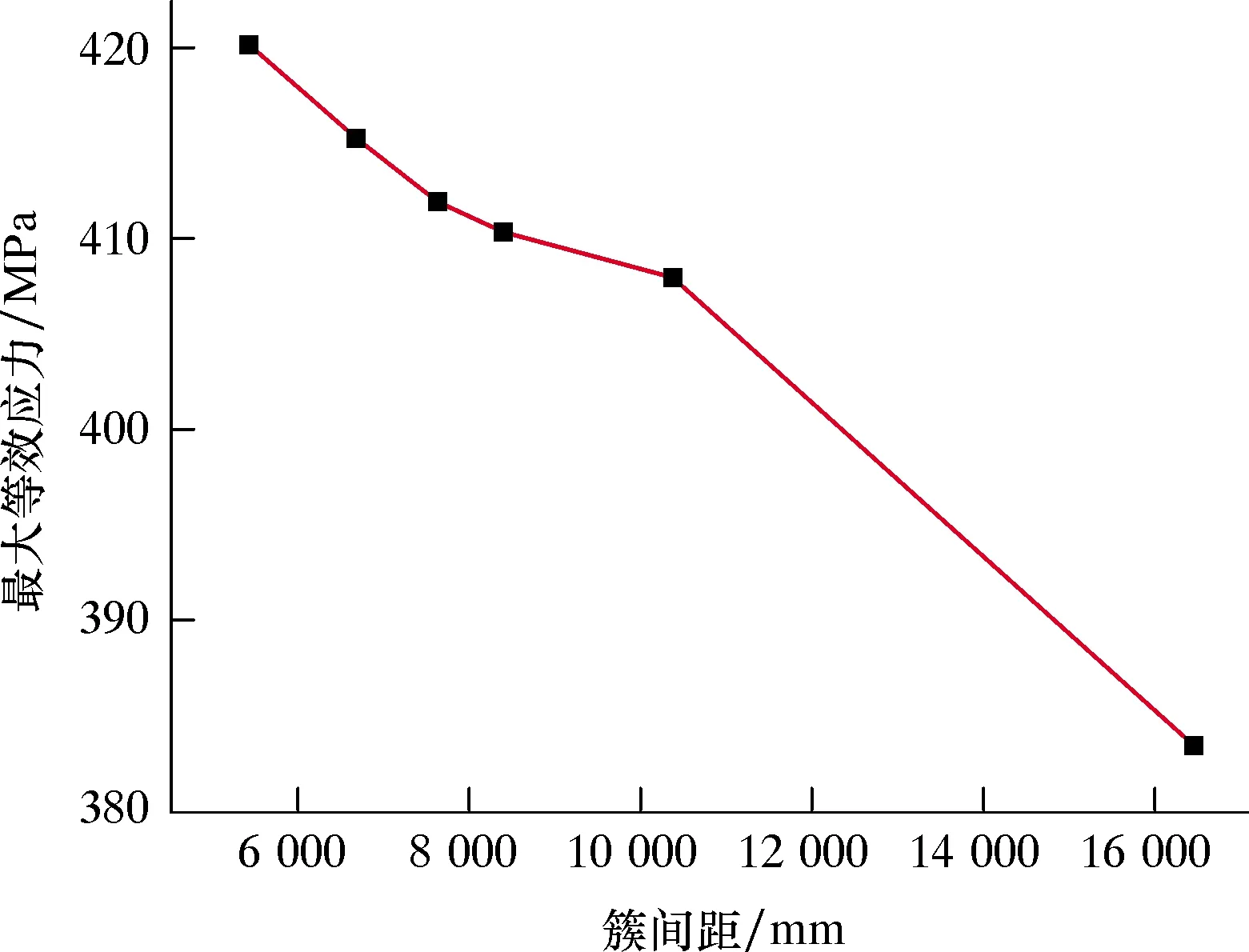
图11 不同簇间距下套管内壁最大等效应力曲线Fig.11 Curve of maximum equivalent stress on inner wall of casing with different cluster spacings

对不同簇间距下套管内壁最大等效应力曲线拟合分析，结果表明，簇间距离与套管内壁最大等效应力呈线性负相关关系，即有：

y=-0.003x+437.405 (R2=0.978)

(1)

该关系式表明，随着簇间距的增加，套管内壁所受最大等效应力的变化趋势会不断下降。这是由于深层页岩气井水平段在压裂过程中，在射孔段会出现应力波动，当两簇之间距离越远时，相互之间的应力影响也越小。

通过对比套管内壁应力极值在不同射孔簇数下的离散程度，可以较为清晰地得出水平段套管在“密簇”压裂工况下应力大小的波动情况。套管内壁应力离散度随射孔簇数的变化曲线如图12所示。套管内壁应力离散度的表达式为：

(2)

式中：e为应力离散度，无量纲；σmax为套管内壁应力最大值，MPa；σmin为套管内壁应力最小值，MPa。

由图12可以看出：随着射孔簇数的增加，应力离散度呈现不断增长趋势;其中在3～ 5簇之间应力离散度增幅较大，在5～7簇之间增幅减小；当射孔簇数为8时，应力离散度达到最大值9.34%，与3簇时相比增幅达到29%，此时套管整体受力更加不均匀，更容易产生屈服变形。由此可见，“密簇”压裂会增加套管所受应力的不均匀度，因此在深层页岩气井压裂增产改造中，应合理设计水平段射簇密度，以满足施工的安全要求。

图12 不同射孔簇数下套管内壁应力离散度曲线Fig.12 Dispersion curve of stress on inner wall of casing with different numbers of perforation clusters

4.3 实例分析

以川南地区威荣区块某水平井为例，该井垂深3 800 m，水平段长1 500 m，共完成20段110簇压裂施工。簇间距介于8.4～12.5 m，最高泵压103.0 MPa，停泵压力60.3 MPa，最大施工排量20 m3/min，平均单段压裂规模2 450 m3，平均加砂量60 m3。该井在第7段位于裂缝不发育段，射孔簇数为8簇，簇间距9.5 m，相较于临近分段射孔簇数更密集。该段第一次电缆泵送遇阻，上提洗井后再次泵送通过，说明该段存在套管变形问题，但变形程度较小，后续顺利完成了变形段的压裂施工。

5 结 论

(1)在深层页岩气井水平段压裂过程中，套管应力呈现出先快速下降后快速上升直至达到稳定的动态趋势，并在泵压稳定阶段达到最大值589.59 MPa。温-压耦合作用可以显著提高套管所受最大等效应力，相较于不考虑温度时，套管应力提升了65.33 MPa。套管应力随着井筒内温差的增大而增加，在相同泵注压力下，井筒温度每下降10 ℃，套管的最大等效应力会增加8 MPa左右。

(2)长时间大排量的泵注压裂液会诱发断层活化滑动，当断层滑移距离超过3 mm时，套管在断层面处开始受到明显的剪切应力，当滑移距离达到5 mm时，套管内壁最大等效应力达到最大值1 430 MPa。套管变形量随滑移距离的增加而不断增大，两者几乎呈线性增长关系。

(3)“密簇”压裂会对套管应力产生明显的影响。簇间距越小，套管所受最大等效应力越大。对不同簇间距下套管内壁最大等效应力曲线拟合分析表明，簇间距与套管内壁最大等效应力呈线性负相关关系。“密簇”压裂会增加套管所受应力的不均匀度，模拟结果表明，射孔簇数从3簇增加到8簇时，应力离散度增幅达29%，因此单段射孔簇数越多，套管整体受力越不均匀，更容易产生屈服变形。