斜滑断层作用下埋地管道局部屈曲失效研究*

陈艳华 吴康康

(1.华北理工大学建筑工程学院 2.河北省地震工程研究中心)

0 引 言

随着经济高速增长和产业结构的迅速变化，我国对油气资源的需求逐步扩大。长输管道作为油气类能源运输载体，不仅高效、便捷，且受气候环境影响较小，损耗低，因此被称为生命线工程。截至2020年，我国累计建设油气长输管线144 000 km，其中然气管线长约86 000 km，原油管道长约29 000 km，成品油管道长约29 000 km。国家“十四五”规划明确提出要构建现代能源体系，加快建设天然气主支管道，完善油气互联互通网络[1-3]。

我国幅员辽阔，地形地貌复杂，绝大多数省份都有油气管道分布，埋地管道不可避免地会穿过地震活动断层。大量震害资料显示，由断层引发的场地永久变形是管道大变形以致屈曲失效破坏的重要原因，因此国内外众多学者针对跨断层埋地管道的安全性开展了大量研究。20世纪70年代，N.M.NEWMARK等[4]首先开始了小位移埋地管道在断层作用下的响应分析，并提出了断层作用下的简化埋地管道模型。随后L.R.L.WANG等[5]在前人的基础上进行改进，提出柔性索假设理论，并对管道的本构关系采用三折线模型来模拟。2000年，冯启民等[6]在高田至郎[7]的模型基础上进行了等效静力试验研究。2008年，白文彪[8]通过制作两箱体模型模拟断层错动，让一个箱体相对于另一个箱体发生位移，实现对埋设于土箱中的管道施加断层位移作用。2009年，薛景宏等[9]通过建立弹簧-管道-土体模型，分析了破碎带宽度、埋深及直径等参数对管道受力的影响。2010年，赵雷等[10]建立了埋地钢质管道在地震作用下的有限元模型，分析了逆断层作用下管道的失效模式。2011年，金浏等[11]研究了逆断层下埋管的整体梁式屈曲及局部壳式屈曲行为，得到各阶段的临界位错距离和屈曲模态。近年来，全恺等[12]通过建立跨断层埋管的三维管土有限元模型，分析了断层位移和管道运行压力等参数下埋地管道的屈曲响应。刘啸奔等[13]分析了逆断层作用下X80高强钢质管道的两种屈曲形式，并讨论了壁厚、埋深及断层倾角等参数对管道屈曲的影响。周晴莎[14]通过多元非线性回归理论得到各类影响因素下，X80材质大口径管道穿越走滑断层和逆断层的埋地管道临界屈曲应变和临界断层位移计算公式。李勐[15]利用有限元仿真，研究了不同参数下跨走滑断层和组合断层下管道的屈曲响应。张杰等[16]通过建立黄土地层管土耦合有限元模型，分析了逆断层下埋地管道的失效模式和变形规律。刘自亮等[17]考虑输氢管道特殊工作环境所产生的氢脆问题，通过试验获得管道在高压输氢环境下的应力-应变数据，模拟研究了埋地输氢管道在走滑断层下的失效模式及屈曲响应。

虽然国内外学者对跨断层埋地管道进行了大量研究，但一般都集中在正断层、逆断层和走滑断层，对既有水平错动也有竖直错动的斜滑断层作用下埋地管道的屈曲失效研究甚少[18]。实际工程中有大量管道会穿越斜滑断层，如我国主导的中国-中亚天然气管道工程穿越 F8 活动断裂带，汶川地震中都江堰虹口地震断层，水平与垂直位移都达到了4.7 m[19]。本文基于ABAQUS有限元软件，建立了三维非线性管土相互作用有限元模型，分析了斜滑断层下断层错动量、运行内压及管道壁厚等影响因素对管道屈曲模式及力学性能的影响，并对比了不同断层类型下管道的临界屈曲位移。研究结果可为工程中跨斜滑断层埋地管道的屈曲判定及设计施工和管道防护提供参考。

1 跨断层管土有限元模型建立及失效准则

不同断层类型如图1所示。管土之间的相互作用既属于耦合问题也属于接触问题[20]。本文基于大型有限元软件ABAQUS，考虑管道与土体的材料非线性，通过非线性接触力学手段模拟管土相互作用，建立管道穿越斜滑断层的整体力学模型。

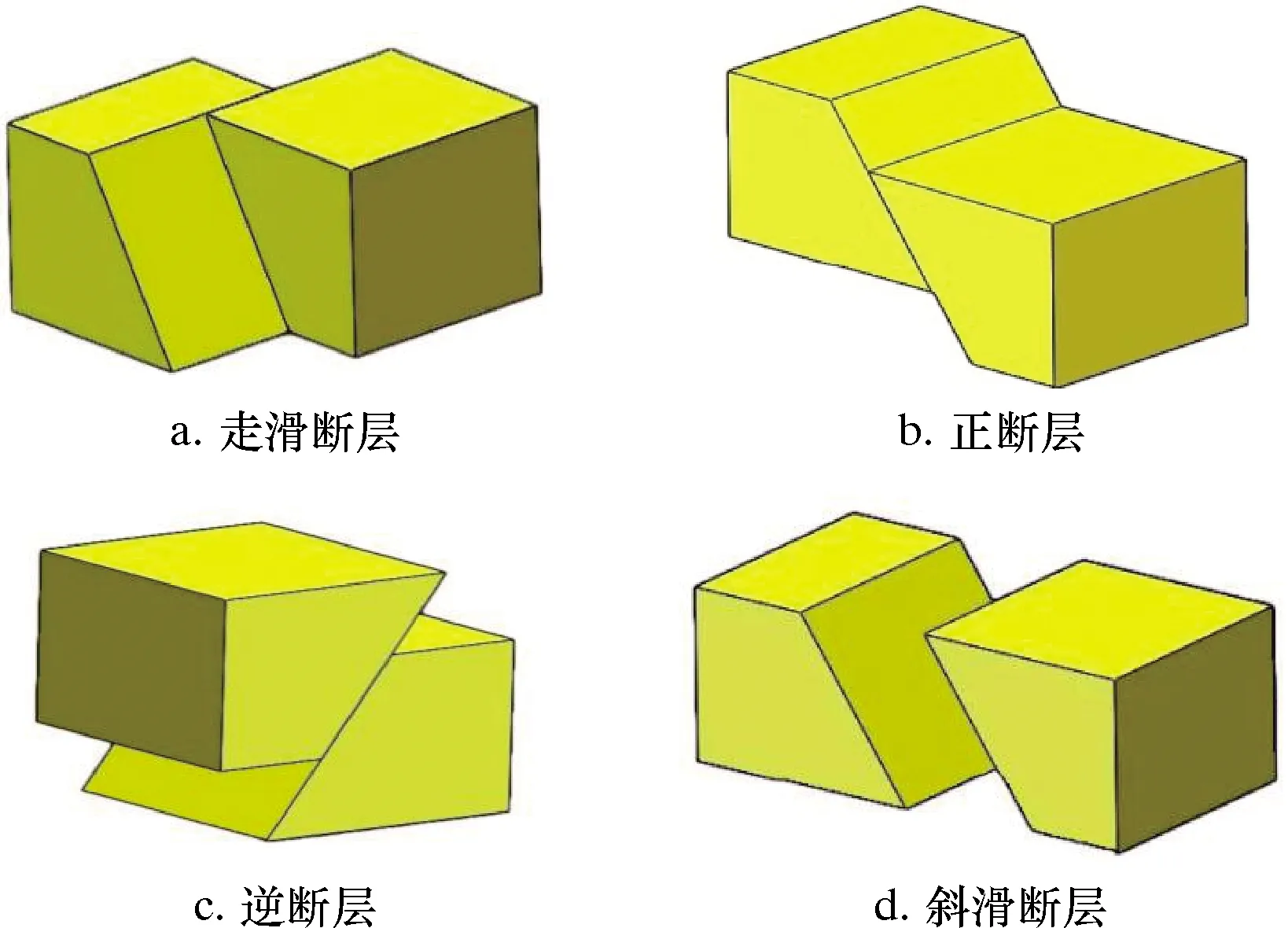
图1 不同断层类型Fig.1 Different fault types

1.1 管土本构关系

本文针对X80高强钢质管道进行研究，管道外径为914 mm，壁厚为8 mm，屈服应力为530 MPa，其真实应力-应变曲线如图2所示。由于断层作用下管道发生屈曲的过程属于大变形问题，所以必须考虑其塑性变形。管材本构采用Ramberg-Osgood模型[21]。回填土模型采用理想弹塑性模型——Mohr-Coulumb模型[22]，其弹性模量为33 MPa，密度为1 400 kg/m3，黏聚力为24 kPa，摩擦角为11.4°。内压是影响管道安全运行的重要因素之一，根据美国机械工程师协会关于输气管道的标准，引入0.72作为安全系数。管道最大运行内压pmax如式1所示。

(1)

式中：σy为钢材屈服应力，MPa；t为管道壁厚，mm；D为管道外径，mm。

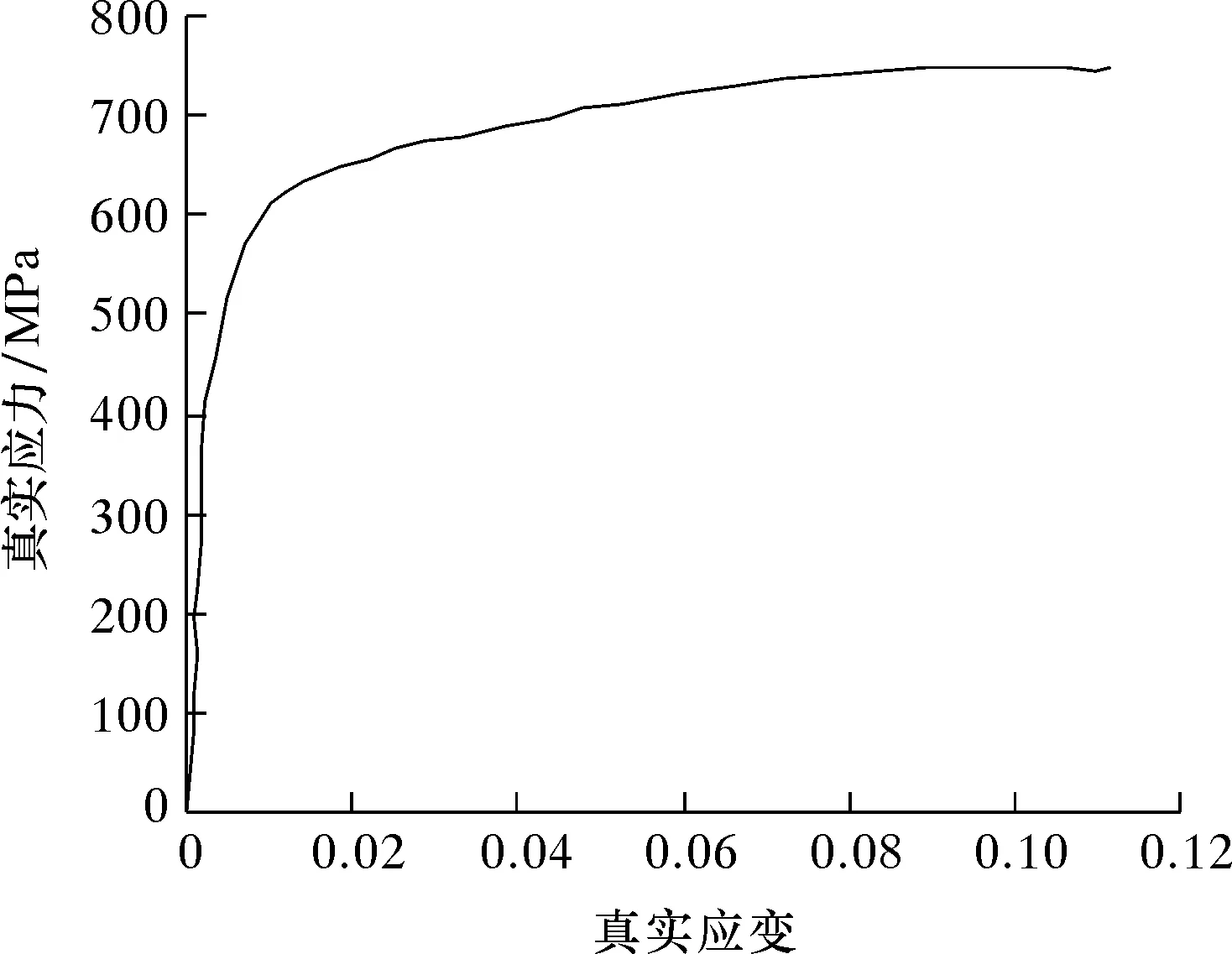
图2 X80管道真实应力-应变曲线Fig.2 True stress-strain curve of X80 pipeline

1.2 模型建立

当管土计算区域长度大于60倍的管径时，可以忽略长度对管道变形的影响[17，21]。本文选取管道计算长度为60 m，土体计算区域为60 m×10 m×6 m，管道埋深为2 m，设置断层角为90°。采用各向同性壳单元(S4R)模拟管道结构，土体模型选用实体单元(C3D8R)离散。管土相互作用采用非线性接触模型，该理论可以较为真实地反映管土相互作用，管土摩擦因数设置为0.3(根据文献[14]有较好的收敛效果)。为了节省运算时间，对管道断层面至管道屈曲位置附近进行局部加密。土体、管道及断面的网格划分如图3所示。

1.3 边界条件及位移载荷设定

本文模拟的是管道穿越斜滑断层，相较于普通的正断层、逆断层及走滑断层更为复杂，其边界条件的设定尤为重要。为了更好地模拟管道受力状态，设置以下边界条件及位移载荷[22]：

(1)如图3a所示，模型上表面为地表面，不需要设置任何约束；

(2)对于右盘土体，在其两侧面施加水平方向(X方向)约束，限制其水平方向运动，然后在其底面施加位移载荷，使其可以沿Y轴正方向移动；

(3)对于左盘土体，在其底面(与上表面对应的另一面)施加竖直方向(Y方向)约束，限制其竖直方向运动，然后在其侧面施加位移载荷，使其可以沿X轴正方向移动；

(4)在模型前、后面节点施加约束，限制其Z方向运动。

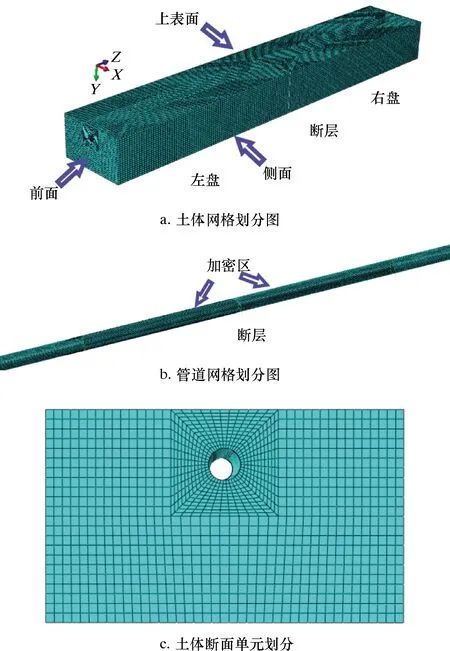
图3 管-土网格划分图Fig.3 Pipeline-soil mesh division

1.4 失效准则

传统基于应力失效的管道设计准则没有充分利用管道强化阶段，偏于保守[23]。长输埋地油气管道多以延性好、强度高的钢管为主，地面发生大变形时，埋地管道易发生弹塑性变形，结合我国《油气输送管道线路工程抗震技术规范》(GB-504078—2017)中“优先采用降低计算应变的措施”的准则，本文采用基于应变的塑性失效准则进行埋地管道失效校核。

2 有限元结果分析及讨论

2.1 断层错动量的影响

图4为无压管道在不同断层错动量下的应力分布图。由图4可知：当错动量为0.6D时管道仅发生弹性变形，随着错动量的增大，在近断层处出现2个应力集中区域并逐渐演变为局部屈曲，断层处管道应力也逐渐增大；断层两侧应力分布相同，两屈曲位置间管道长度逐渐被拉大，而两端部管道受断层错动影响较小；管道变形曲线随错动量的增大逐渐由光滑的“S”形变成有明显拐点的“Z”形。

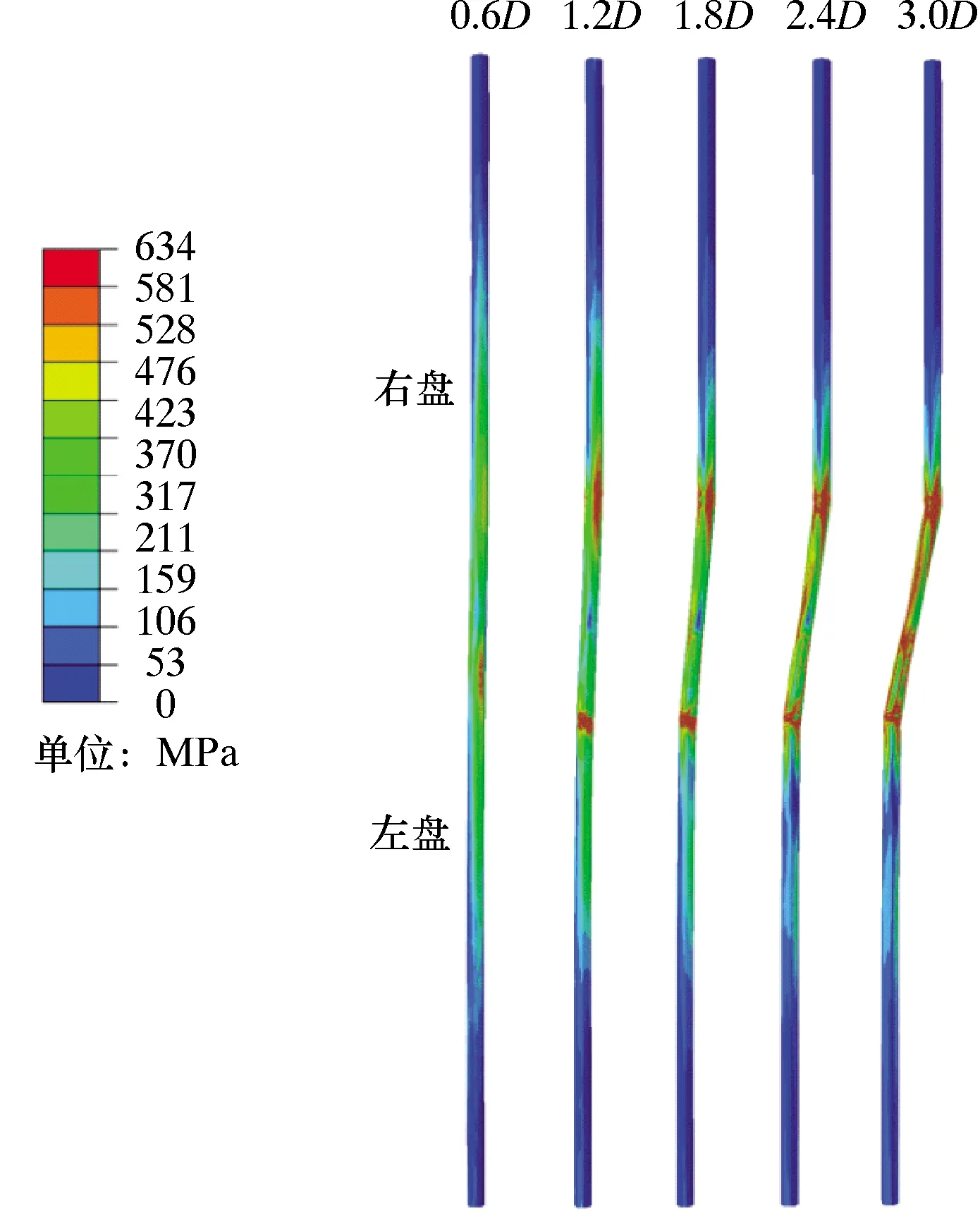
图4 无压管道应力分布图Fig.4 Stress distribution of pressureless pipeline

图5 管道最大轴向压缩应变随断层错动量的变化曲线Fig.5 Change curve of maximum axial compressive strain with fault dislocation

图5为管道最大轴向压缩应变随断层错动量的变化曲线。从图5可以看出，管道初始应变较小，在断层位移小于0.9D时曲线增长缓慢，当错动量大于0.9D时管道的应变发生了突变，其变化幅度超过1倍，认为此时管道发生了屈曲。分析表明，随土体断层位移的增长，基岩裂隙引起的应变能也越大，管道所受土体传递的能量越大。由于断层错动而带来的附加弯矩，使管道在变形曲率最小处产生应力集中并发生屈曲。

2.2 内压的影响

当管径为914 mm、壁厚为8 mm时，通过计算可得管道最大运行压力pmax=6.68 MPa，本文取最大内压为6 MPa。假定内压沿管道长度方向没有压力损失，为一定值。本文选取无内压，内压1、2、3、4、5及6 MPa共7种不同工况，研究内压对管道局部屈曲行为的影响。

图6为不同内压下管道在错动量为2.25D时的应力分布及局部屈曲模式图。

图6 不同内压下管道应力分布及局部屈曲模式图Fig.6 Pipeline stress distribution and local buckling modes under different internal pressure

从图6可以看出：当运行压力小于2 MPa时，管道的屈曲模式为局部压溃，且应力集中区域较大；当内压达到3 MPa时，左右两盘管道屈曲模式均由局部压溃变为起皱，管道应力集中面积也变小。分析可知，管道在局部屈曲部位出现起皱实现了应力释放，吸收了大量能量，因此管道应力集中面积变小。通过对比，左右两盘管道随内压增大其屈曲位置变化亦有不同。对于左盘管道，随着内压增大其屈曲位置距断层距离变化较小；对于右盘管道，当运行压力小于2 MPa时，屈曲位置变化较小，当内压介于2～5 MPa时，管道屈曲位置距断层距离随内压增大逐渐减小，当内压大于5 MPa而小于6 MPa时其距离逐渐增大。

图7为不同内压下管道最大轴向压缩应变随断层位移变化曲线。由图7可知：管道的初始应变受内压影响较大，随内压的变大近似呈线性增长。无内压管道在断层位移下最先发生屈曲，随后不同内压管道相继发生屈曲；当内压小于3 MPa时，管道发生屈曲的临界断层位移随内压增大逐渐增加；当内压大于3 MPa时，其临界断层位移均为1.35D。内压增大虽然增大了管道的初始应变，但也使管道发生屈曲的临界位移变大。因此，内压在某种程度上增强了管道的抗屈曲能力。

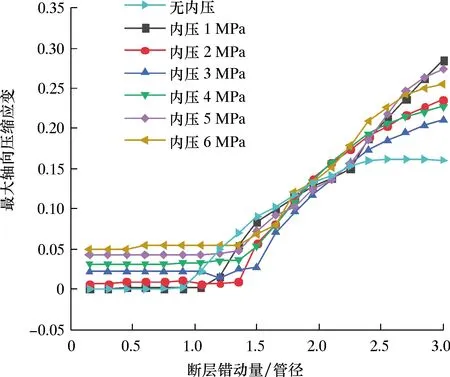
图7 内压对管道最大轴向压缩应变的影响曲线Fig.7 Influence of internal pressure on maximum axial compressive strain of pipeline

2.3 管道壁厚的影响

本研究为X80大口径高强钢质管道，外径为914 mm，根据实际长输管道数据及研究需要，选定壁厚为8、10、12、14及16 mm共5种，研究壁厚对管道屈曲行为的影响。图8为内压4 MPa、错动量2.55D时管道的应力分布图。从图8可知，随着壁厚的增大，管道局部屈曲现象逐渐消失，并在断层两侧形成2个较大范围的应力集中区域，且右盘略大于左盘，但两端部管道受断层影响较小。

图9为壁厚对管道最大轴向压缩应变的影响曲线。从图9可知：在斜滑断层作用下，壁厚对管道应变影响较大；小壁厚管道初始应变较大，随着壁厚增大应变逐渐减小，当断层错动量为1.35D时，壁厚为8 mm的管道最先发生屈曲；随着壁厚增大，屈曲时刻轴向应变的快速增长阶段也在逐渐向后推移，其他壁厚管道随后相继发生屈曲，16 mm厚壁管道随着错动量的增加其应变变化平缓，在模拟中并未发生屈曲(错动量小于3.00D)。

图8 不同壁厚管道应力分布图Fig.8 Pipeline stress distribution with different wall thicknesses

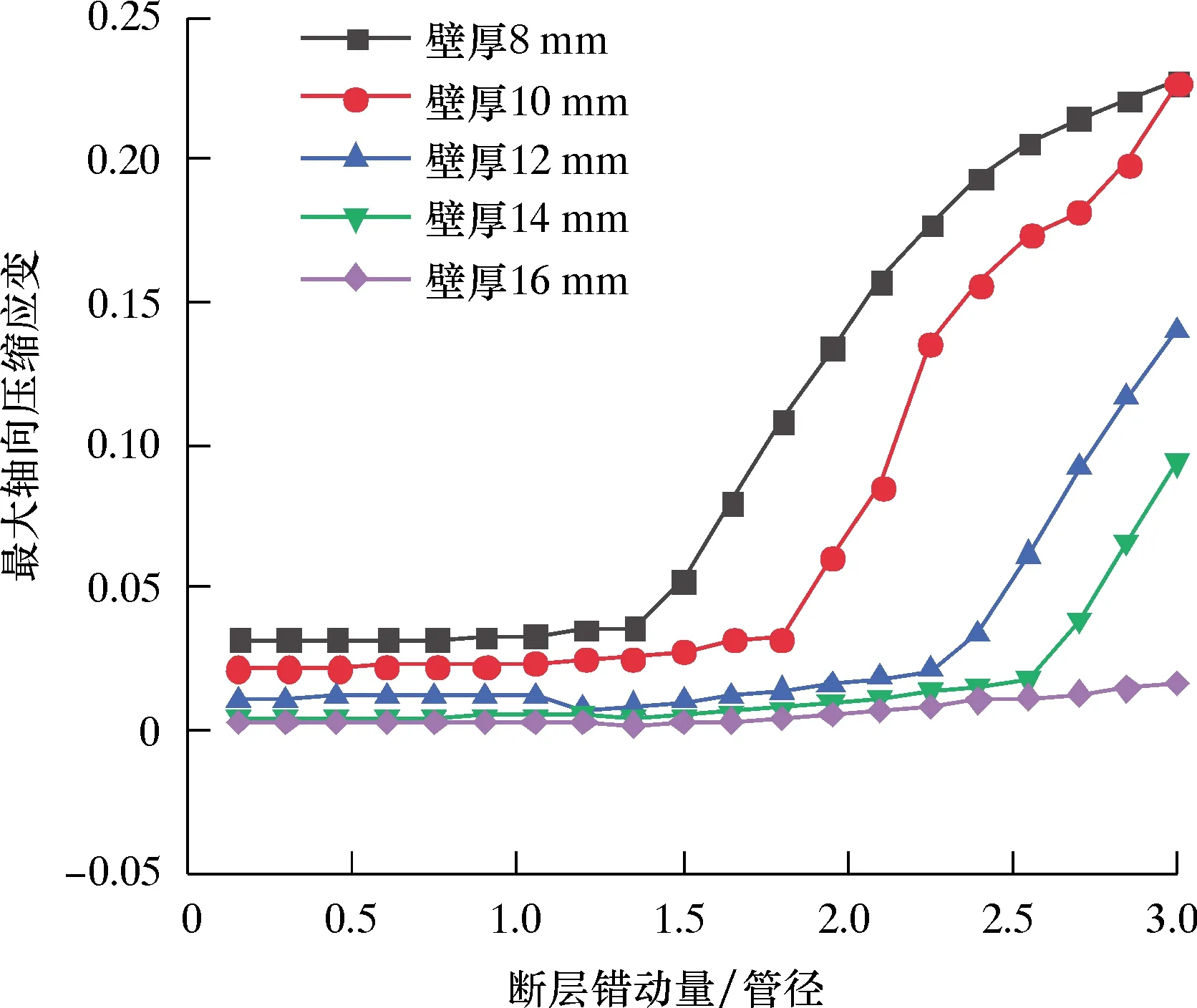
图9 壁厚对管道最大轴向压缩应变的影响曲线Fig.9 Influence of wall thickness on maximum axial compressive strain of pipeline

增加管道壁厚，其横截面积增加，整体刚度提升，因此在管径一定的情况下，适当增大管道壁厚有助于增强斜滑断层错动下管道的抗屈曲能力。

2.4 不同断层类型屈曲对比

图10为不同断层类型下管道最大轴向压缩应变曲线。从图10可以看出：不同断层下管道的初始应变差异较小，当断层错动量小于1.35D时，应变曲线均平缓增加且增速较慢，近似呈线性变化；当错动量达到1.35D时，斜滑断层曲线发生突变，曲线增长呈明显的非线性，此时斜滑断层下的管道最先发生屈曲；随着错动量的增加，不同断层类型下的管道相继发生屈曲，其临界断层位移分别为1.35D、1.65D、1.80D及2.40D。由模拟结果可知，斜滑断层下管道的临界屈曲位移远小于单一的走滑断层和倾滑断层，破坏后其应变亦大于其他断层，因此在实际工程中，应针对斜滑断层下的管道制定更加严格的防护措施。

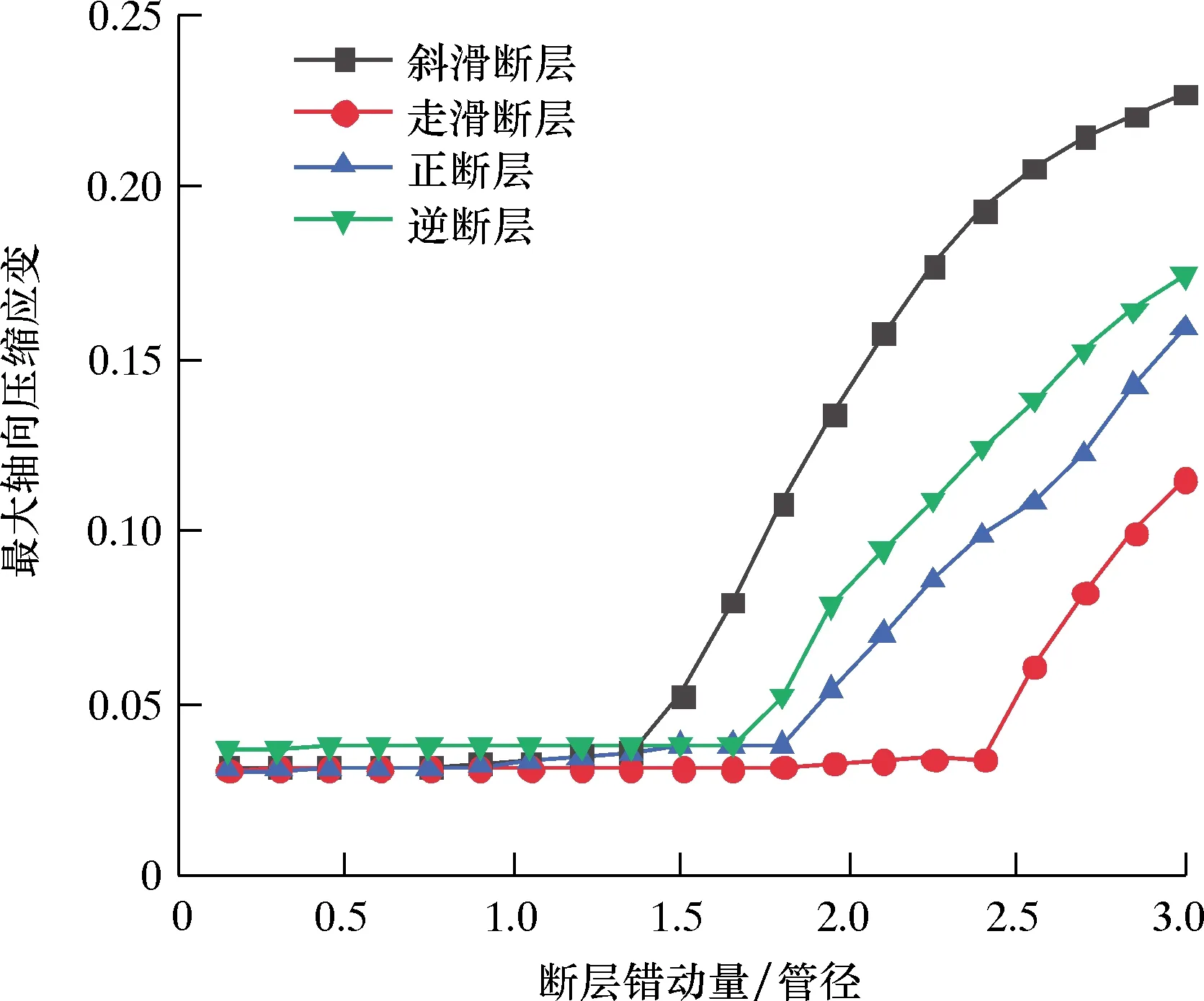
图10 不同断层类型下管道最大轴向压缩应变曲线Fig.10 Maximum axial compressive strain curve of pipeline under different fault types

3 结 论

(1)斜滑断层作用下管道局部屈曲位置与走滑断层和倾滑断层类似，都位于断层两侧，而非断层处；管道的变形曲线也由光滑的“S”形变为有明显拐点的“Z”形。随着错动量增大近断层处管道受力与变形也越大，而远断层处管道受断层位移影响较小。

(2)当内压小于3 MPa时，管道在斜滑断层作用下的失效模式为局部压溃，而内压达到3 MPa时，管道失效模式变为起皱。内压作用下虽然管道初始应变增大，但使管道发生屈曲时的临界断层位移增加，在一定意义上相当于增强了管道的抗屈曲能力。

(3)基于模拟结果，当管道外径一定时，随着壁厚的增大，管道屈曲现象逐渐消失，出现2个较大范围的应力集中区域。壁厚增大使管道承受断层错动的能力增强。

(4)通过对比不同断层类型下管道应变曲线，在同等条件下，斜滑断层最先发生屈曲，逆断层次之，走滑断层最后。