含缺陷的高压弯管冲蚀特性影响研究*

张永学 何 涛 樊建春 张来斌 张金亚 祁紫伟

(1.中国石油大学(北京)机械与储运工程学院 2.中国石油大学(北京)安全与海洋工程学院)

0 引 言

水力压裂是国内外油气田生产时广泛采用的一项增产增注措施，其中高压弯管是压裂作业中必不可少的设备[1]。压裂过程产生的冲蚀现象，主要由高速高压流体和固体颗粒与弯管壁面经过长时间冲刷切削所引起。长期的冲蚀会引起弯管的结构变化，形成不同形状的冲蚀缺陷结构，而这些冲蚀缺陷又会反过来影响弯管内部的流动，导致弯管的冲蚀特性发生改变[2]。

国内外学者针对弯管冲蚀问题进行了大量研究。张继信等[3]针对油气开采过程中压裂液对单个高压弯管的冲蚀破坏问题，采用数值模拟方法对弯管的冲蚀磨损特性进行了计算分析，研究结果表明，压裂液对高压弯管冲蚀较为严重的区域在弯头的外弧内壁处，颗粒动力黏度、颗粒质量流量和颗粒粒径等都对弯管的冲蚀率有较大影响。邱福寿等[4]为解决稠油热采井中凹坑缺陷对四通管的冲蚀影响，采用CFD模型进行了冲蚀损伤及损伤发展规律研究，研究结果表明：当凹坑位于直管段时，对四通管冲蚀磨损影响不大；当凹坑位于肩部位置且凹坑较浅时，四通管冲蚀磨损急剧增大。H.POURARIA等[5]针对弯头的冲蚀磨损情况，采用数值模拟方法研究了不同管径等影响因素对冲蚀率的影响，研究结果表明，弯头的冲蚀率与管道内径、流体流速和颗粒粒径有关。压裂过程中高压弯管的运行安全性与稳定性对于保障油气田开采具有重要意义，因此对高压弯管的冲蚀磨损进行研究很有必要。

本文根据弯管处冲蚀缺陷位置及类型，建立含冲蚀缺陷的高压弯管三维几何模型，运用Fluent软件对其进行了冲蚀特性数值模拟，对比有、无缺陷时高压弯管冲蚀磨损情况，分析了不同缺陷因素对冲蚀特性的影响。研究结果可为高压弯管冲蚀磨损的安全预警提供参考。

1 冲蚀磨损数值模拟模型

1.1 液相流动方程

高压弯管输送的介质为携带支撑剂的含砂压裂液，它的运动可简化为液固两相流，其中液相为水基压裂液，固相为固体支撑剂颗粒。由于压裂液中固相的体积分数通常小于10%，所以在使用Fluent模拟时，液相可看作连续相，固相可视为离散相。液相的流动方程包括连续性方程、动量方程和湍流模型方程，各方程具体形式如下[6]。

连续性方程：

(1)

式中：ρ为流体(连续相)密度，ui为与坐标轴xi平行的速度分量。

动量方程：

(2)

式中：p为静压力，τij为黏性应力张量，g为重力加速度，Fi为广义体积力。

RNGk-ε湍流模型计算使用范围广，计算量适中且具有较高的计算精度，广泛适用于弯管处壁面弯曲率较高的数值计算，其方程如下[7]：

Gk+Gb-Ym-ρε

(3)

(4)

式中：k为湍流动能，μt为湍流黏度，μ为流体动力黏度，Gk为平均速度梯度产生的湍流动能，Gb为浮力产生的湍流动能，Ym为可压缩湍流波动扩张对整体耗散率的影响，ε为湍流动能耗散功率，σk为湍动能k的湍流普朗特数，σε为耗散率ε的湍流普朗特数。

Fluent软件中默认值为C1ε=1.42、C2ε=1.68、C3ε=1.83。

1.2 颗粒相运动方程

高压弯管中由于固体颗粒的体积分数小，所以可忽略颗粒间的相互碰撞，采用DPM(Deformable Part Model)模型对固体颗粒进行冲蚀数值模拟计算。离散相模型中颗粒的动力学方程为[8]：

(5)

式中：up为颗粒速度分量，ρp为颗粒密度，FD为颗粒受到的流动阻力，Fp为颗粒所受的其他作用力。

颗粒所受的其他作用力为：

(6)

(7)

式中：dp为颗粒直径，Re为相对雷诺数，CD为阻力系数。

1.3 冲蚀磨损方程

针对高压弯管的冲蚀情况，本文选用冲蚀率为基准进行分析对比，采用DPM模型进行计算，以液体作为连续相，采用欧拉-拉格朗日方法为基础求解其流动方程；以固体颗粒为离散相，通过微分方程求解颗粒运动状态变化，从而得到颗粒运动轨迹和能量传递变化。冲蚀率计算模型为[9]：

(8)

式中：mp为颗粒平均质量流量；N为颗粒与结构壁面碰撞时的数量；C(dp)为颗粒直径函数，通常与被冲蚀材料的物理性质相关，本文取1.8×10-9；α为颗粒运动路径与结构壁面间的冲击角度；f(α)为颗粒的冲击角函数；v为颗粒的相对速度；b(v)为颗粒相对速度函数，本文固体颗粒为石英砂，取值2.6[10]；Aface为颗粒碰撞管壁面的壁面面积；Rerosion为单位时间内单位面积上颗粒对结构壁面的冲蚀磨损质量。

高压弯管冲击角函数f(α)采用Huser和Kvemvold提出的模型[11]，具体参见文献[11]。

εn=0.993-0.030 7α+4.75×10-4α2-

2.61×10-6α3

(9)

εt=0.998-0.029α+6.43×10-4α2-

3.56×10-6α3

(10)

2 含缺陷高压弯管数值模型建立

2.1 冲蚀缺陷类型及几何模型确定

通过对现场高压弯管的冲蚀失效元件对比分析和相关文献的查阅，可以将缺陷的凹坑类型大致分为两类[13]。图1为两种不同凹坑缺陷截面形状示意图。第一类为矩形凹坑，通常由固体颗粒对高压弯管壁面进行均匀切削而形成，凹坑三维形状近似椭圆柱；第二类为抛物线凹坑，由流体和固体颗粒的运动方向发生改变后冲蚀而形成，凹坑三维形状近似为椭圆体。

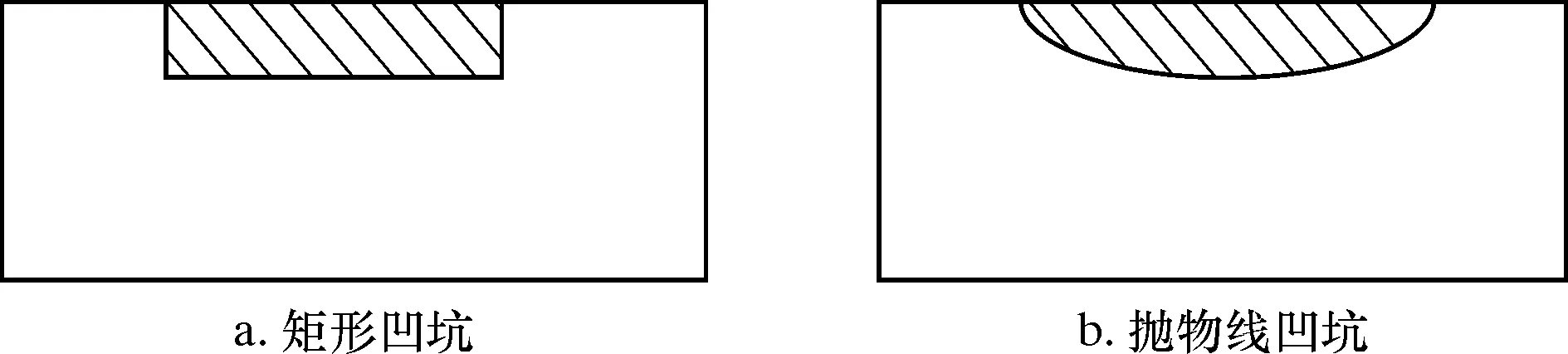
图1 凹坑缺陷截面形状示意图Fig.1 Schematic diagram of section shape of pit defects

矩形凹陷主要分布在直管段，且缺陷由冲蚀磨损和腐蚀破坏共同造成。本文流体为水基压裂液，无腐蚀性，根据对现有高压弯管失效元件的统计和对比，抛物线凹坑多于矩形均匀凹坑，故本文以标准椭圆球为缺陷模型，如图2所示。图2中a为缺陷长度，b为缺陷宽度，c为缺陷深度。高压弯管选取90°弯头，弯管内径69.85 mm，曲率半径145 mm，进、出口直管段长取10倍弯管内径；弯头处缺陷长度5 mm，缺陷宽度4 mm，缺陷深度1 mm，弯管外侧内壁轴向角度45°，如图3所示。流体域入口为速度入口，速度值为10 m/s，出口为压力出口，压力值为105 MPa。压裂液采用水基压裂液，在模拟设置中选取滑溜水，密度为1 000 kg/m3，黏度为0.001 Pa·s;高压弯管壁面材料选取40CrMo，密度为7 850 kg/m3。作为支撑剂的固体颗粒选取石英砂，密度为3 300 kg/m3。

图2 半椭球型缺陷示意图Fig.2 Schematic diagram of semi-ellipsoidal defects

2.2 网格无关性验证

将图3中含缺陷弯管几何模型进行布尔运算，得到高压弯管流体域几何模型。对流体域进行非结构化网格单元划分，为了进一步提高网格质量，完成整体网格划分后再对弯头部分进行网格加密，最后对缺陷位置的网格进行更为精细的网格加密，如图4所示。

图3 弯管缺陷位置示意图Fig.3 Schematic diagram of elbow defect positions

对高压弯管的流体域模型进行网格无关性验证，一方面可以减少由于网格大小不同所导致的计算错误，另一方面可以在保证模拟结果准确的前提下降低计算成本[14]。以最大冲蚀率为标准进行验证，结果如表1所示。由表1可知，当网格数达到48万后，模拟结果趋于稳定，所以本文采用方案4进行数值模拟计算。

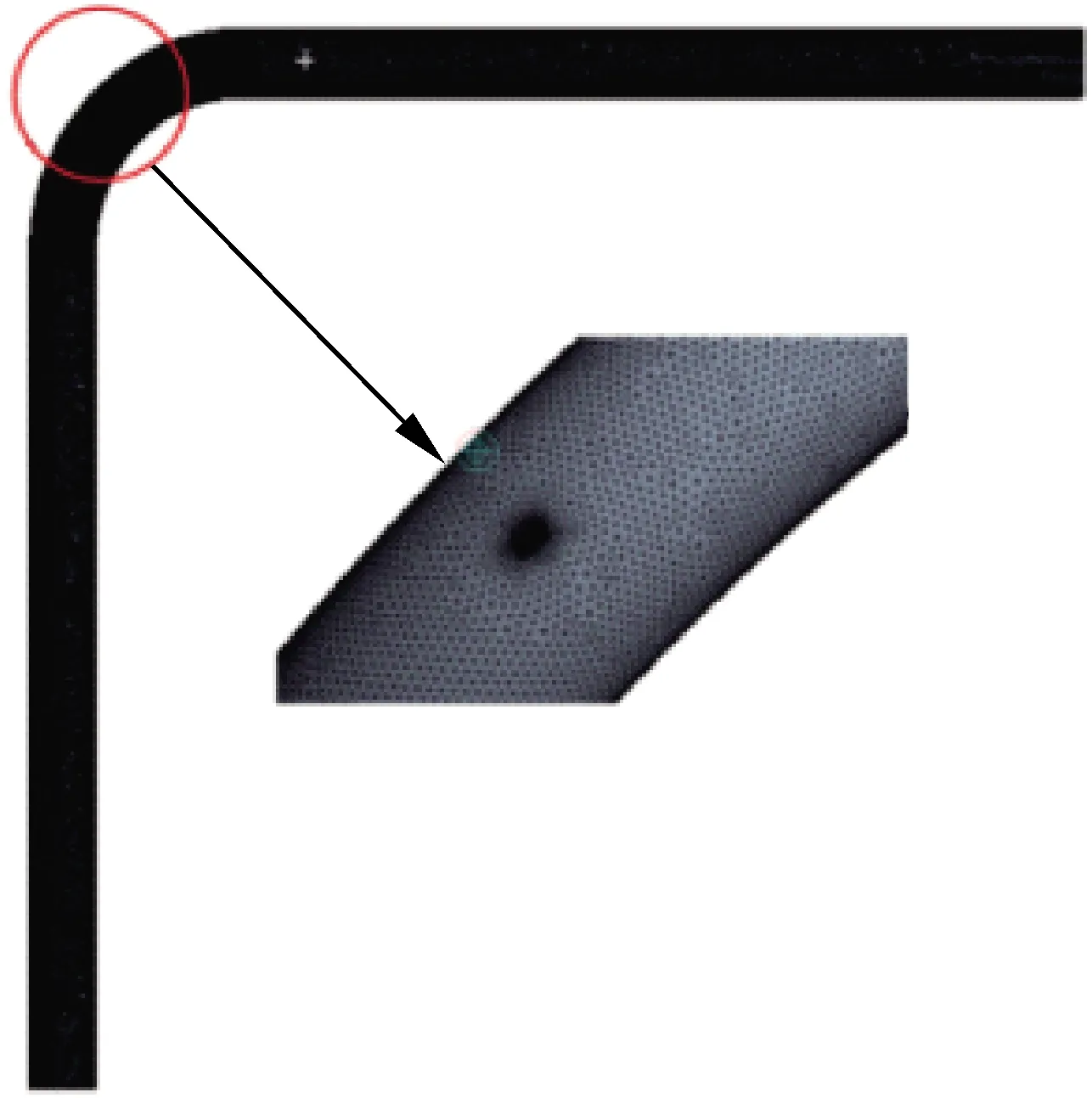
图4 含缺陷弯管网格划分图Fig.4 Mesh division of elbow with defects

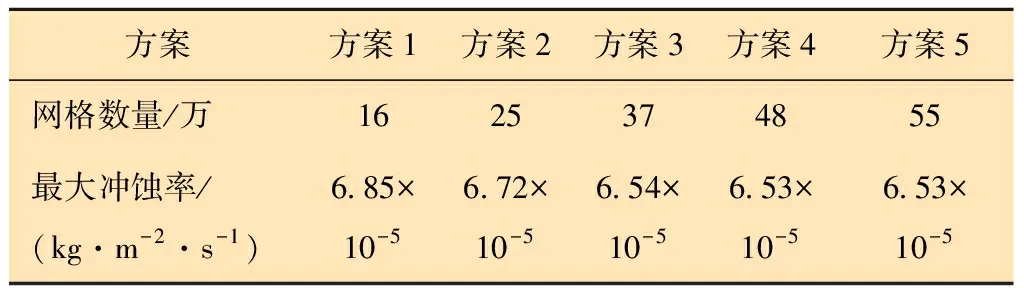
表1 网格无关性验证结果Table 1 Mesh independence verification results

2.3 冲蚀模型验证

为验证数值模拟计算的准确性，本节采用文献[15]中的弯管冲蚀试验数据进行数值模拟，并将模拟计算结果与文献中的试验结果进行对比，以验证数值模拟的可靠性。试验弯管内径为40 mm，上游和下游直管段长度均为280 mm，曲率半径为100 mm，流体密度为1 000 kg/m3，颗粒密度为2 650 kg/m3。

高中生的地理教学十分重要，应该引起所有教育事业者的注意。同时也应该加强学生的核心素养的培养，坚持对学生进行素质教育，以将学生培养为高素质、高学识、高修养的“三高”人才而努力奋斗。

图5为数值模拟结果与文献中的试验结果对比曲线。由图5可知：试验结果与模拟结果变化趋势基本一致，均随着速度增大，最大冲蚀率不断增大；试验结果与数值模拟结果的最大误差为9.6%，试验的最大冲蚀率要明显大于数值模拟中的最大冲蚀率。分析认为，在试验过程中，随着冲蚀时间的延长，弯管壁面会产生细微的冲蚀缺陷，含冲蚀缺陷的弯管最大冲蚀率要大于初始弯管的最大冲蚀率，故在试验测量中，失质量法所测量的质量损失比预期要大。

图5 数值模拟结果与试验结果对比曲线Fig.5 Comparison curve between numerical simulation results and test results

3 有、无冲蚀缺陷高压弯管冲蚀特性对比

图6为无缺陷条件下高压弯管冲蚀率云图。由图6可知，颗粒对管路入口直管段和出口直管段的冲蚀磨损作用相对弯头小很多，由于入口直管段处压裂液沿着管道方向做直线流动，流动方向未发生改变，固体颗粒对管壁冲击较少。而在弯曲部位，由于压裂液的流动方向发生改变，冲击弯管外侧内壁面，造成较大磨损。磨损的主要区域不在弯头外侧壁面的前半部分，而在外侧壁面的后半部分并延续到弯头出口附近的下游直管。这是因为在弯头外侧壁面处固体颗粒并非直线运动，而是在弯管结构的影响下做曲线运动冲击弯管外侧壁面，避开了弯头的前一小部分，所以磨损区域主要分布在弯头外侧壁面后半部分。

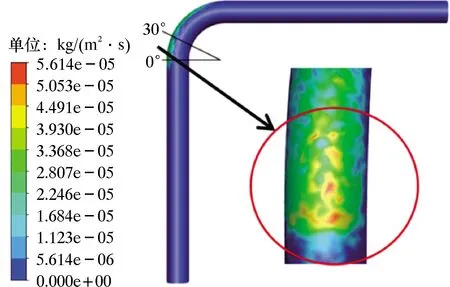
图6 无缺陷条件下高压弯管冲蚀率云图Fig.6 Cloud chart of erosion rate of high-pressure elbow without defects

图7为缺陷条件下高压弯管冲蚀率云图。由图7可以看出，含缺陷弯管的最大冲蚀率为3.8×10-4kg/(m2·s)，远大于完整弯管最大冲蚀率5.6×10-5kg/(m2·s)。图8为缺陷位置速度矢量局部放大图。

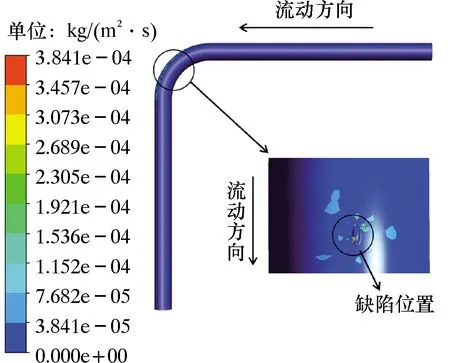
图7 含缺陷条件下高压弯管冲蚀率云图Fig.7 Cloud chart of erosion rate of high-pressure elbow with defects

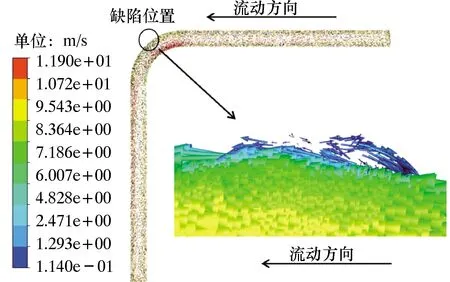
图8 缺陷位置速度矢量局部放大图Fig.8 Local enlargement of velocity vector at defects

由图8可以发现，在缺陷位置流动不稳定，进入缺陷区域的压裂液一部分随主流方向继续流动，一部分产生回流冲击缺陷壁面。分析认为，由于压裂液在缺陷处的流动状态更为紊乱，使得固体颗粒冲蚀壁面现象更为复杂，缺陷壁面处的固体颗粒速度更大，单位时间内撞击壁面的次数更多，冲击动能增大，导致缺陷处冲蚀最为严重。

4 不同缺陷因素对高压弯管冲蚀特性的影响

4.1 缺陷长度

缺陷区域对高压弯管的正常使用存在较大影响，参考相关文献[16]，缺陷长度选取4、5、6、7和8 mm。图9为缺陷长度与最大冲蚀率的关系曲线。由图9可以发现，在高压弯管的缺陷宽度和深度不变的情况下，缺陷处的最大冲蚀率随着缺陷长度的增加而增大。由于缺陷处固体颗粒沿流动方向冲刷壁面的区域更长，缺陷区域内部流动更加复杂，产生的回流现象增多，使得颗粒冲蚀壁面更为紊乱，导致颗粒单位时间冲击壁面次数增加，冲击动能变大，故冲蚀磨损现象更加明显。

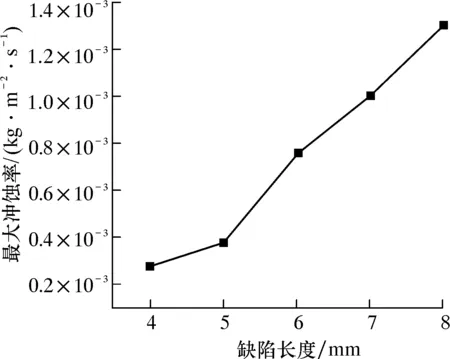
图9 缺陷长度与最大冲蚀率的关系曲线Fig.9 Relationship curve between defect length and maximum erosion rate

4.2 缺陷宽度

参考相关文献[15]，缺陷宽度选取1、2、3、4和5 mm。图10为缺陷宽度与最大冲蚀率的关系曲线。由图10可以发现，在高压弯管缺陷长度和深度不变的情况下，缺陷宽度较小时，缺陷处的最大冲蚀率随着缺陷宽度的增加急速减小，由于此状态下长宽之比较大，冲蚀率受到缺陷长度因素的影响较大，导致冲蚀率有较大幅度变化；随着缺陷宽度继续增大，最大冲蚀率缓慢减小，逐渐趋于平稳，虽然缺陷宽度增大，弯管截面的速度矢量变化较小，使得缺陷处流动情况基本无改变，导致冲蚀率变化较为平稳。

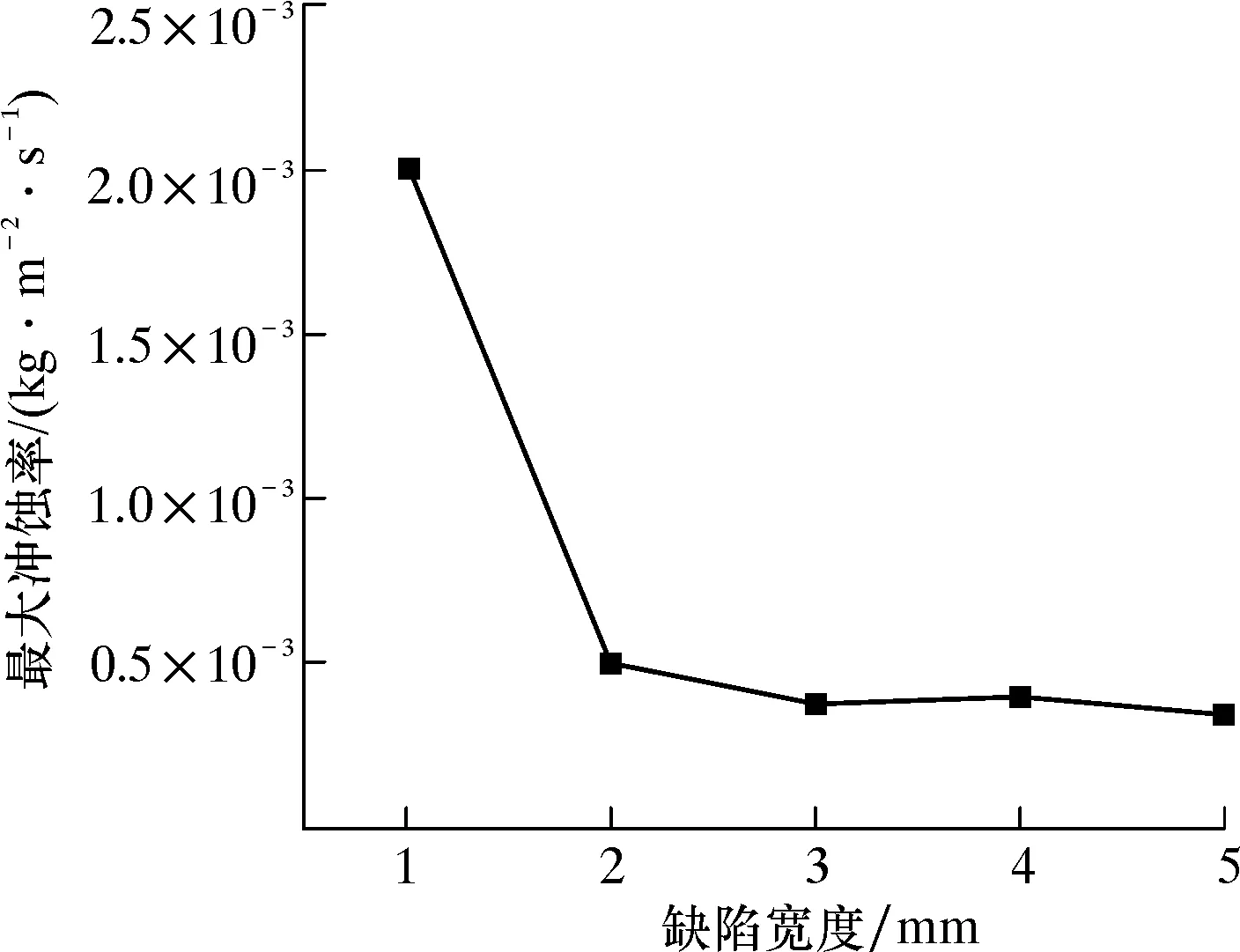
图10 缺陷宽度与最大冲蚀率的关系曲线Fig.10 Relationship curve between defect width and maximum erosion rate

4.3 缺陷深度

参考相关文献[15]，缺陷深度选取0.50、0.75、1.00、1.25和1.50 mm。图11为缺陷深度与最大冲蚀率的关系曲线。由图11可以发现，在高压弯管缺陷长度和宽度不变的情况下，随着缺陷深度增大，最大冲蚀率不断减小。由于缺陷深度增大，缺陷处的内压逐渐增大，部分固体颗粒未到达缺陷壁面处就随着压裂液流出缺陷区域，单位时间内固体颗粒冲刷缺陷区域内壁面的个数减少，颗粒的冲击动能减小，导致冲蚀磨损减轻。

图11 缺陷深度与最大冲蚀率的关系曲线Fig.11 Relationship curve between defect depth and maximum erosion rate

4.4 轴向角度

分析不同轴向角度对含缺陷弯管冲蚀特性的影响，选择弯头外壁内侧轴向角度区间为0°～90°，具体选取0°、15°、30°、45°、60°、75°和90°，如图3所示。分别从弯管外侧内壁面0°～90°每隔15°处选取一个模型进行数值模拟，得到如图12所示的关系曲线。由图12可知，在0°、15°和30°处的最大冲蚀率较高。这是因为在无冲蚀缺陷的模拟中(见图6)，冲蚀较大的区域在这一段轴向角度，此区域颗粒碰撞次数多，颗粒对壁面的冲蚀现象更为明显，故缺陷在此角度范围时的冲蚀率较大。45°、60°和75°处最大冲蚀率较小且变化较为平稳，主要原因是无缺陷弯管在此轴向角度区域的冲蚀率较小，故缺陷在此角度范围时的冲蚀率较小且变化不大。

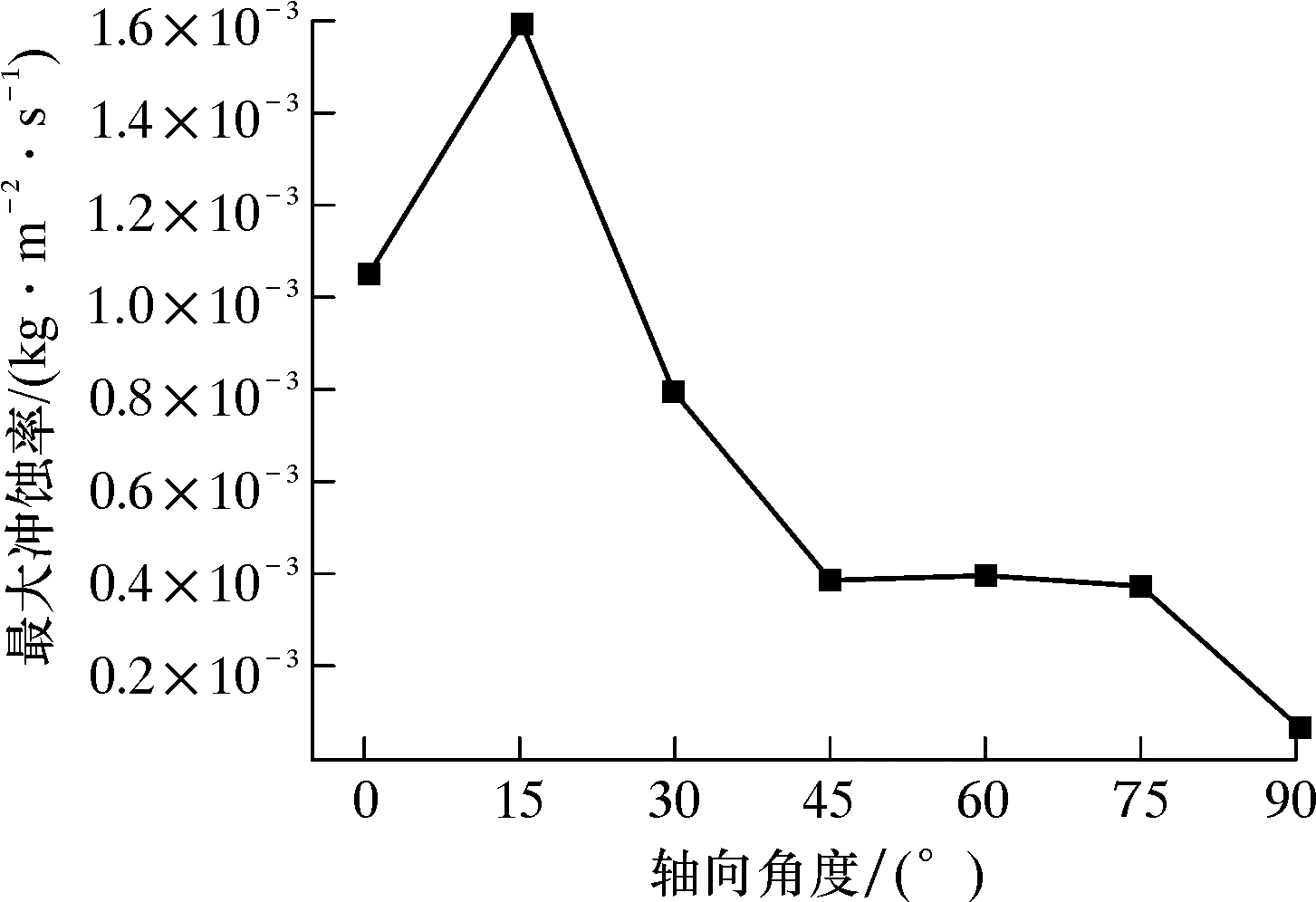
图12 轴向角度与最大冲蚀率的关系曲线Fig.12 Relationship curve between axial angle and maximum erosion rate

4.5 两个缺陷中心轴向距离

分析两个缺陷中心轴向距离对含缺陷弯管冲蚀率的影响，设置两个形状相同的冲蚀缺陷，如图13所示，将第一个冲蚀缺陷位置固定在60°处，第二冲蚀缺陷位置向45°方向移动，两个缺陷的中心轴向距离分别为5、15、25、35、45和55 mm。将第一个冲蚀缺陷设在60°的主要原因是，通过对不同轴向角度的分析发现，缺陷轴向角度在45°～75°时冲蚀率变化较为稳定，而0°～30°的冲蚀率变化较大，为了避免轴向角度对两个缺陷中心轴心距离的影响，故将两个缺陷的轴向角度设置在45°～60°之间。

图13 两个不同轴向缺陷位置示意图Fig.13 Schematic diagram of defect positions with two different axial angles

图14为缺陷轴向距离与最大冲蚀率的关系曲线。由图14可以发现，随着两个缺陷中心轴向距离的增大，最大冲蚀率呈现上升趋势，但是上升较为平缓，可以推测两个缺陷中心轴向距离对最大冲蚀率的影响不大。

为了研究缺陷中心轴向距离和轴向角度之间的影响，本节做两组对照模拟计算。由于缺陷在30°时冲蚀率较大，故设两个算例的轴向中心距离相等，分别设两个冲蚀缺陷轴向位置为30°+45°和45°+60°。通过计算发现30°+45°处最大冲蚀率为10.3×10-4kg/(m2·s)，45°+60°处最大冲蚀率为5.8×10-4kg/(m2·s)。由此可知，缺陷中心轴向距离对冲蚀率的影响并不大，主要影响因素是轴向角度。

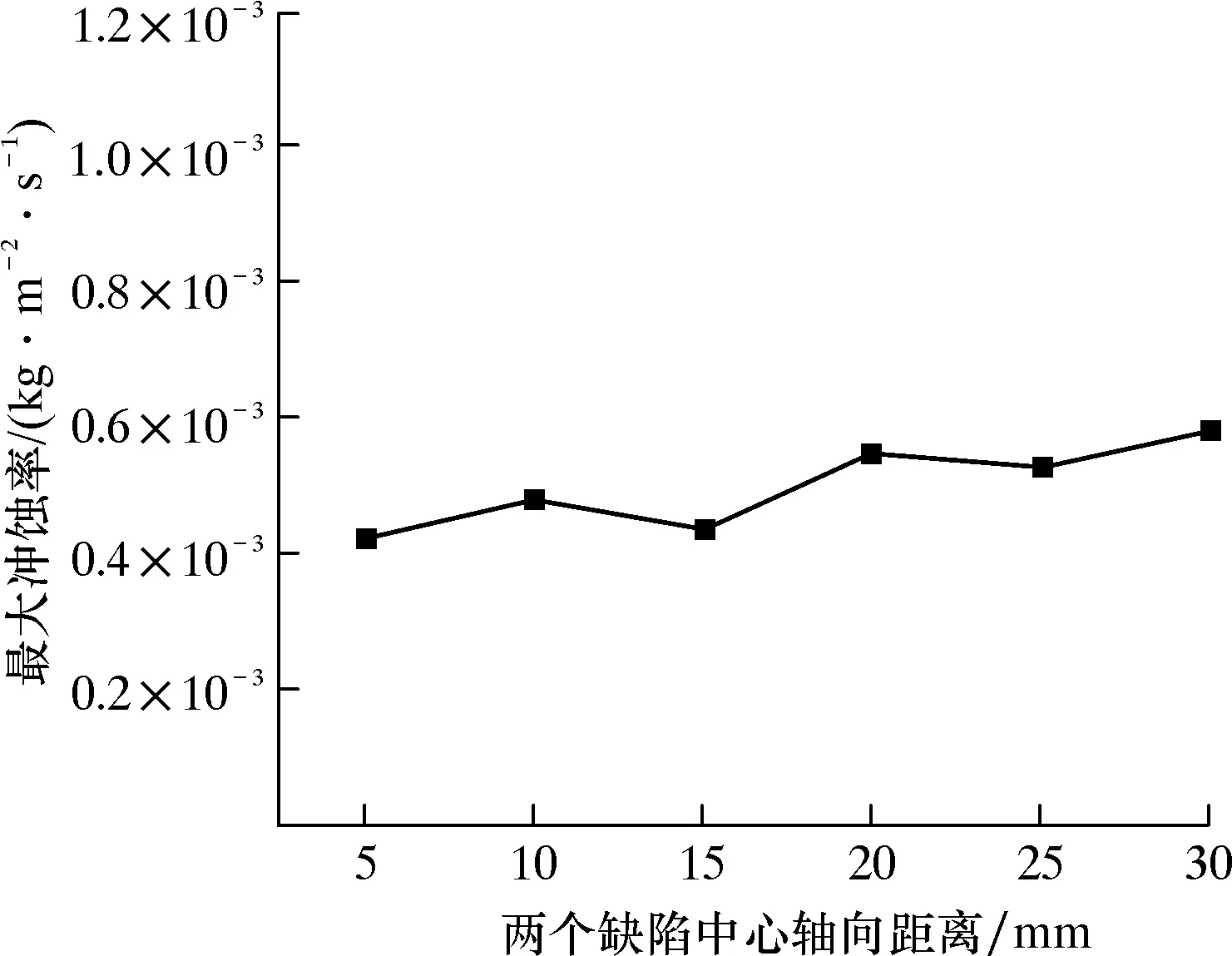
图14 缺陷轴向距离与最大冲蚀率的关系曲线Fig.14 Relationship curve between defect axial distance and maximum erosion rate

5 结 论

(1)无缺陷高压弯管冲蚀磨损较为严重的区域在弯头外侧处，此区域最大冲蚀率远大于入口与出口直管段区域。

(2)含缺陷高压弯管冲蚀磨损较为严重的区域在缺陷处，且含缺陷弯管最大冲蚀率约是无缺陷弯管的6倍。故在实际应用中，冲蚀导致的失效事故主要由冲蚀缺陷的产生所引发。

(3)含缺陷高压弯管的最大冲蚀率随着缺陷长度的增大而增大；随着缺陷宽度的增大，最大冲蚀率减小；随着缺陷深度的增大，最大冲蚀率逐渐减少。最大冲蚀率的增大会导致冲蚀更加严重，增大缺陷区域范围。随着冲蚀时间的延长，冲蚀磨损导致壁面脱落速度更快，达到极限壁厚的时间更短，导致其使用寿命缩短。

(4)缺陷位置在弯头0°、15°和30°处的最大冲蚀率较大，45°、60°和75°处的最大冲蚀率较小且变化较为平稳。故在压裂作业中要时刻关注弯管缺陷位置，尤其是集中在0°～30°处的缺陷，此范围内的冲蚀率较大，会导致冲蚀磨损现象加重，从而缩短弯管的使用寿命。最大冲蚀率随着两个缺陷轴向中心距离的增大而小范围波动且变化较小。