高速列车交会激励下雨棚振动响应
2022-06-09冯海龙李红梅王域辰史伟华
冯海龙,王 博,李红梅,王域辰,史伟华,张 骞,4
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心,北京 100081;3.青岛大学 机电工程学院,山东 青岛 266071;4.中车青岛四方机车车辆股份有限公司 高速列车系统集成国家工程实验室,山东 青岛 266111)
目前,国内外学者针对高速列车的气动载荷及其对雨棚等铁路临近结构的振动响应进行了大量探索试验和研究。Maeda等[1]采用实车试验的方法,研究了列车运行时车身周围的空气动力学特性。Fujii等[2]研究了两车交会情况下列车周围的空气动力学特性。Khayrullina等[3]采用大涡模拟法,研究了隧道内列车单车通过站台时列车风对站台的影响。Hemida等[4]采用数值模拟和大涡模拟的方法,研究了列车周围的流场分布。Gerhardt等[5]研究高速列车通过站台时临近结构受到的列车风载荷,并提出了控制列车风的方法。Hur等[6]采用数值模拟与风洞试验相结合的方法,研究高速列车通过时站房表面列车风载荷分布特点。Baker等[7]研究了列车单车过站时铁路临近结构的气动压力。朱志辉等[8]以天津西客站为例,研究了高速列车通过时“站桥合一”大型客运站的振动响应。唐意等[9]和米宏广[10]采用模态叠加等理论方法,对特定车站的雨棚结构进行了振动响应分析。罗尧治等[11]运用有限元法,对北京北站站台大跨度张弦桁架雨棚结构进行受力分析。颜锋等[12]研究了列车通过时航站楼振动的幅值大小和时程特点。周志勇等[13]采用动网格数值模拟和风洞测压试验2种方法,研究列车经过时雨棚所受风压的变化规律。杨娜等[14]采用Fluent软件,模拟分析雨棚表面风压分布规律、脉动特性以及雨棚自身结构对风压值的影响。杨惠东等[15]运用流固耦合技术,研究无站台柱雨棚在变化流场中的变形和应力情况。以往的研究中,一般只考虑单车通过时列车风致临近结构的振动响应,然而针对两车交会这种不利工况下雨棚的振动响应研究较少,而且针对气动载荷或轮轨力等对雨棚振动响应起主导作用载荷及其相关规律也缺乏研究。
本文采用流体动力学软件Fluent和多体动力学软件Simpack,分别仿真计算获得激扰雨棚的外部载荷,然后在有限元软件Abaqus中建立雨棚结构模型,输入上述外部载荷,分析列车以不同速度级交会时雨棚振动响应,掌握雨棚振动规律,为后期高铁车站雨棚运维提供理论支撑。
1 雨棚结构动力仿真模型
1.1 雨棚结构模型建立
为了研究雨棚的振动响应规律,以某高铁站站台雨棚为研究对象,建立雨棚结构动力仿真模型。雨棚总长421 m,总宽58.9 m,外侧支柱高度11.6 m,内侧支柱高度12.56 m,站台高1.43 m,基础厚度1.5 m。平行股道方向标准跨为18 m,中间跨为21 m。雨棚支柱为钢管柱,共有104根;雨棚内侧纵梁为箱型截面梁;外侧纵梁为工字型梁。建模时,雨棚结构基础底部采用固结约束,雨棚与纵梁之间采用“TIE”连接,采用实体单元C3D8R。雨棚主体构件材料属性及截面尺寸见表1,雨棚整体结构模型如图1所示。

表1 雨棚结构主体构件材料属性及截面尺寸

图1 雨棚结构动力仿真模型
模型中,雨棚内、外侧支柱分别采用直径402 mm、壁厚12 mm和直径800 mm、壁厚14 mm的钢管,外侧纵梁采用截面尺寸为高450 mm、宽300 mm、水平壁厚12 mm、竖直壁厚12 mm的箱型梁,内侧纵梁和横梁采用高750 mm、宽300 mm、水平壁厚12 mm、竖直壁厚16 mm的工字梁;雨棚长422 m,宽58.9 m,厚51.8 mm。
1.2 雨棚结构模态分析
雨棚结构的固有频率是雨棚固有动力特性的综合反映,对雨棚结构进行模态分析在一定程度上能够反映雨棚结构有限元模型的正确性,是动车组气动载荷和轮轨力激励下振动响应分析的基础。
采用有限元软件Abaqus,对雨棚结构进行模态分析。在许多实际工程问题中只需要求解前几个低阶自振频率就能够得到较为满意的精度,因此计算时仅选取有限元模型前5阶振型的自振频率,结果见表2,前5阶振型如图2所示。

表2 雨棚结构自振频率


图2 雨棚结构振型
由表2和图2可知,雨棚的前5阶自振频率表现为低频振动,且振动频率较为集中。
2 外部激励计算
2.1 气动载荷计算
基于三维非定常黏性流动的雷诺平均Navier-Stokes方程并结合k-ε两方程湍流模型[16],运用动滑移网格技术,对动车组在雨棚中交会产生的非定常气动效应进行研究。
为了计算动车组在雨棚中交会的气动载荷,采用Fluent软件,建立8节编组的CR400AF型动车组,其中受电弓、转向架影响范围更多是近场或局部范围,而该雨棚最低高度为11.6 m,距离受电弓、转向架相对较远,且转向架产生的气压集中在车体底部,还会受到站台阻挡,对顶部雨棚影响较小,因此忽略受电弓、转向架等对计算结果影响较小的细部结构。建立的CR400AF型动车组模型如图3所示。

图3 CR400AF型动车组模型
在仿真计算过程中,用有限区域模拟无限大现场环境。在保证计算时间和精度的前提下,对整个模型进行简化,外流场区域宽度100 m(大于10倍车宽),长度2 452 m,站房距线路中心36 m;两动车组为头尾形状相同的流线型车体。整个流场分成均采用结构化六面体网格的若干子块,通过多次改变网格疏密程度,消除网格相关性,网格数量达到一定量级后计算结果趋于稳定,单车体模型网格数约1 000万个,整体模型网格数约6 000万个。建立的计算区域模型(含站房)如图4所示,车体网格模型如图5所示。

图4 计算区域模型

图5 车体网格模型
为了获得较为准确的气动载荷,得到动车组等速交会时雨棚所受气动载荷时程曲线,并分析其分布规律和变化特征,在雨棚上设置280个监控点,实时输出雨棚所受的气动载荷。雨棚网格及监控点布置模型如图6所示。图中监控点序号从左上角起始,第1排1—46,第2排47—92,第3排93—138,第4排139—142,第5排143—188,第6排189—234,第7排235—280。

图6 雨棚网格及监测点布置模型
2.1.1 试验验证
本文主要研究的是动车组在雨棚位置交会时的工况,但现场实测时很难监测到动车组在雨棚中交会,尤其是薄弱位置交会时的气动载荷数据,因此通过对比动车组单车通过雨棚时的监测数据和仿真数据验证数据的准确性。
现场采用CYG1721风压传感器监测雨棚所受气动载荷。风压传感器布置如图7所示。图中:F1-1,F1-2和F1-3为安装在第1跨的风压传感器;F2,F3,F4和F12分别为安装在第2,3,4和12跨的风压传感器。

图7 风压传感器布置位置
风压传感器测得的动车组以350 km·h−1速度通过雨棚时气动载荷极值数据如图8所示。
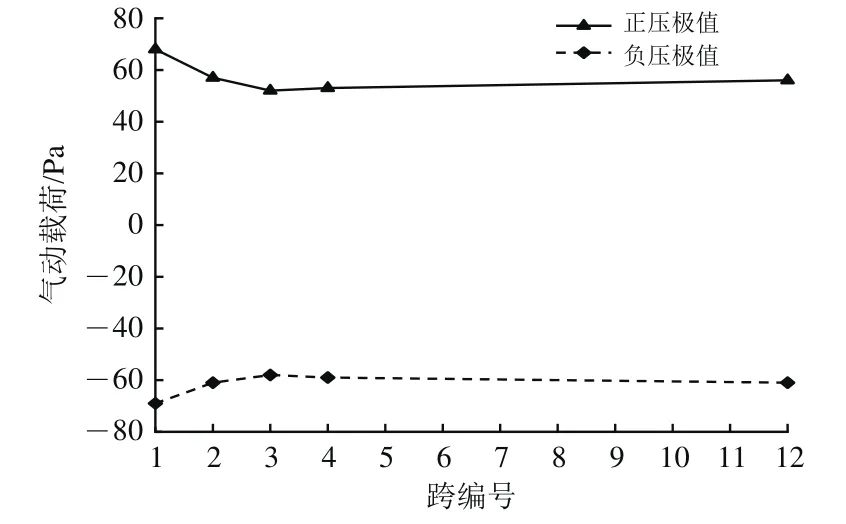
图8 实测气动载荷数据
通过仿真计算得到的雨棚前4跨和第12跨所受气动载荷极值见表3。

表3 雨棚所受气动载荷极值
由表3和图8可知,仿真得到的气动载荷极值与现场实测数据基本一致,最大误差为4.9%,验证了仿真模型合理可靠。
2.1.2 仿真计算
分别计算动车组以200,250,300,350,400和450 km·h−1速度交会时气动载荷分布及变化规律。动车组以不同速度级等速交会时,雨棚上280个监控点监测的气动载荷极值和峰峰值见表4,其中动车组以350 km·h−1速度级在雨棚中部等速交会时的气动载荷云图如图9所示。

图9 350 km·h-1交会速度下气动载荷云图
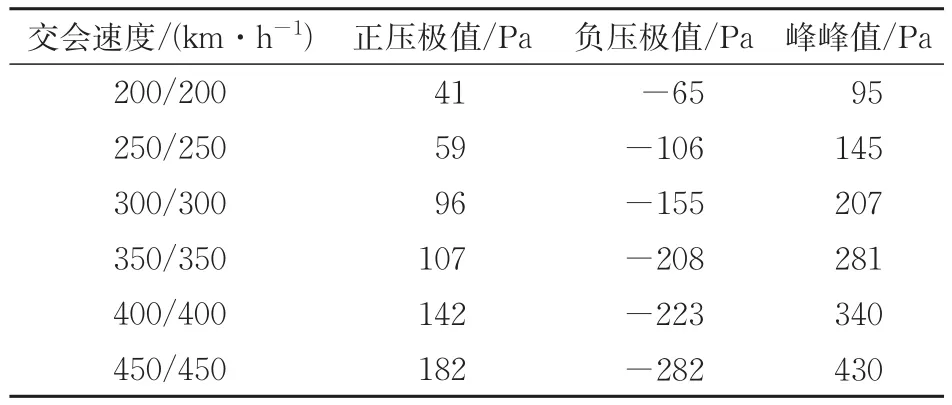
表4 交会工况下雨棚所受气动载荷
由表4可知,动车组在不同交会速度工况下雨棚所受气动载荷负压极值绝对值最大,气动载荷随着车速的增加而增大。
根据表4数据,对雨棚所受气动载荷极值和峰峰值与车速的关系进行拟合,得到拟合曲线如图10所示。

图10 动车组不同交会速度下雨棚所受气动载荷极值
由图10可知,某动车组以不同速度级等速交会时,雨棚所受气动载荷极值与速度的1.61~1.84次方成正比。
为了研究气动载荷沿雨棚不同方向分布规律,以动车组350 km·h−1速度级在雨棚中间位置交会工况为例,分析气动载荷时程曲线以及气动载荷沿雨棚长度、宽度和高度方向的分布规律。
动车组在雨棚中间位置交会时雨棚中间位置和入口位置监控点监测到的气动载荷时程曲线如图11所示。

图11 雨棚中间和入口位置气动载荷时程曲线
由图11可知:动车组在雨棚中间位置交会时,车头车尾通过时雨棚所受气动载荷会出现明显波动,因此当动车组在雨棚中间位置交会时会出现先正后负然后由负转正的气动载荷;而雨棚入口位置监控到的是单车通过时雨棚所受气动载荷,这是由于交会1车和对向驶来的交会2车经过入口位置监控点的时间不同所导致的,因此动车组通过雨棚入口位置时会出现2次先正后负然后由负转正的气动载荷。
雨棚沿长度方向的气动载荷极值分布规律如图12所示,其中第1排与第7排,第2排与第6排,第3排与第5排的监控点沿线路中心线对称分布。

图12 雨棚沿长度方向气动载荷分布
由图12可知,当动车组在雨棚中间位置等速交会时,雨棚长度方向所受气动载荷极值近似于以线路中心线为中心对角对称分布,且负压极值绝对值大于正压极值。
雨棚宽度方向入口和中间位置的气动载荷极值分布规律如图13所示。
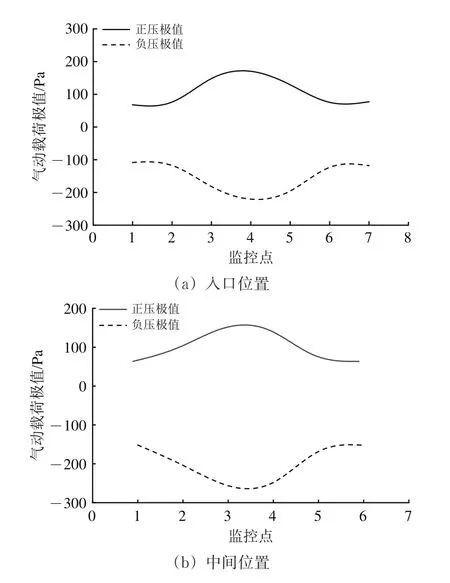
图13 雨棚宽度方向入口和中间位置气动载荷极值
由图13可知:雨棚宽度方向所受气动载荷近似于以线路中心线为轴对称分布,中间位置雨棚所受的气动载荷极值最大;雨棚宽度方向上,一侧是站房,另一侧是开放出口,靠近站房位置的气动载荷极值略小于远离站房位置的气动载荷极值,但是两者差别很小,这主要由于该站房离正线距离较远,且其长度相比雨棚短很多,站房对雨棚所受气动载荷影响较小,可忽略不计。
在雨棚支柱上选取距轨面不同高度的监控点,分析雨棚沿高度方向的气动载荷极值分布规律,其中雨棚内侧支柱水平方向距离线路中心6 000 mm,内侧支柱高度12.56 m,得到不同高度监控点的气动载荷极值见表5,拟合的关系曲线如图14所示。

表5 350 km·h-1交会速度下沿高度方向气动载荷极值

图14 CR400AF型动车组350 km·h-1交会时沿高度方向气动载荷极值
由表5和图14可知,气动载荷极值随着雨棚支柱高度的增加而减小,可以看出最高点(雨棚支柱顶点)的气动载荷极值较最低点(站台平齐高度)减小60%以上。
2.2 轮轨力计算
动车组运行时产生的轮轨力主要包括轮轨垂向力和轮轨横向力,正线通过时轮轨横向力比轮轨垂向力小很多,而且单就轮轨垂向力而言,其受车速影响极为明显[17]。因此,主要考虑轮轨垂向力的作用。为了获得动车组轮轨垂向力,采用Simpack软件,建立8节编组的CR400AF型动车组车-轨耦合动力学仿真模型。动车组采用10个自由度二系悬挂弹簧阻尼单元模拟,且车体、转向架和轮对均考虑竖向振动,车-轨耦合简化模型如图15所示。
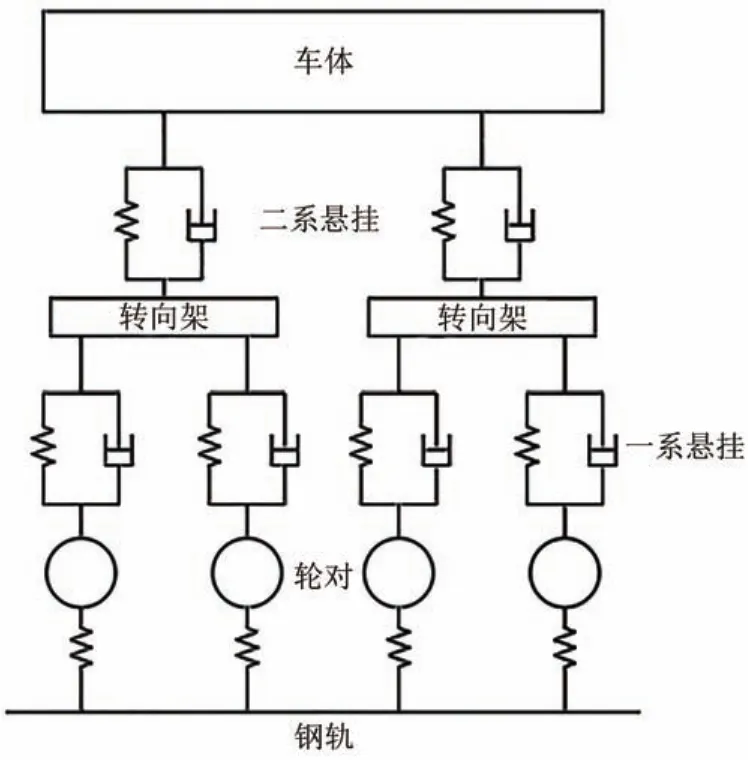
图15 车-轨耦合简化模型
轨道不平顺采用我国高速铁路无砟轨道不平顺谱[18],如图16所示。
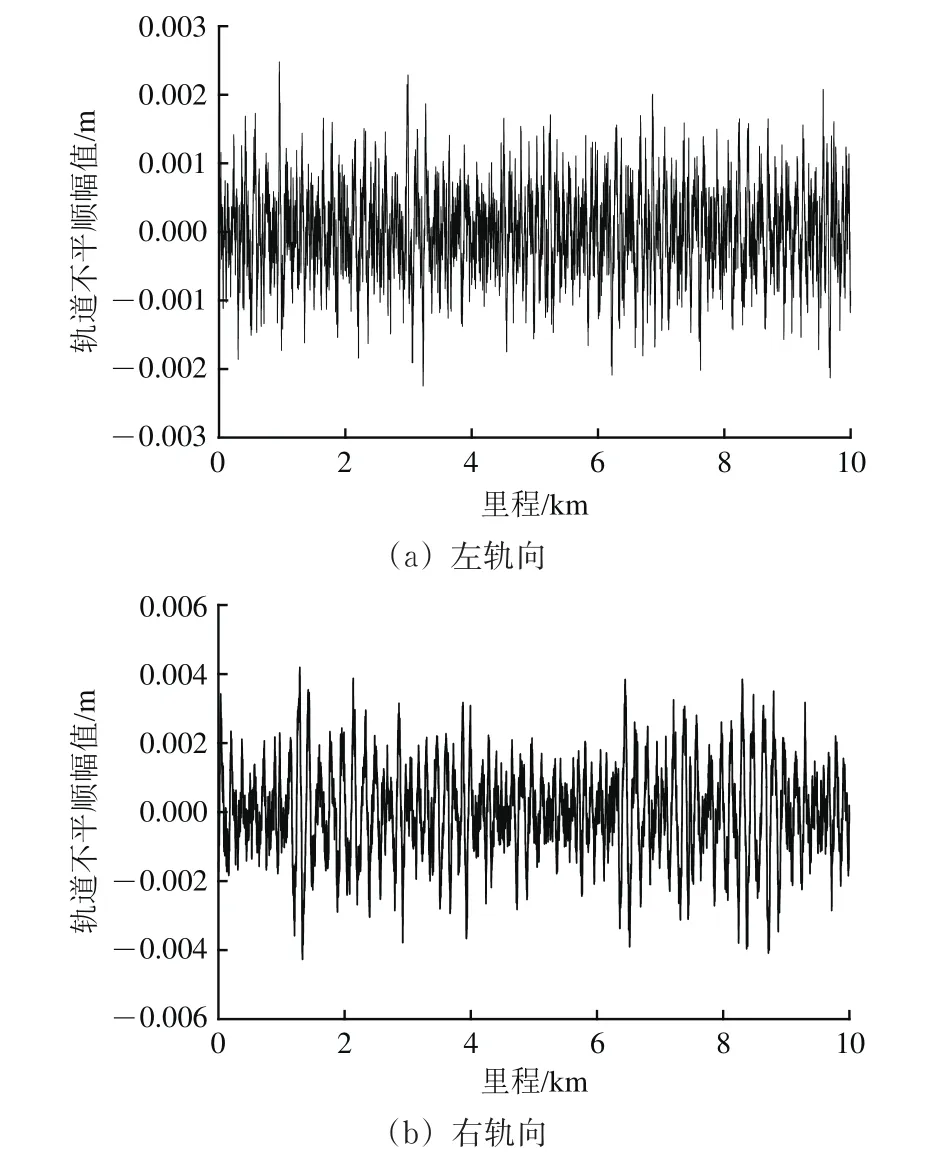
图16 轨道不平顺谱
通过仿真计算得到不同速度级下的轮轨垂向力,详见表6。

表6 动车组不同速度级下的轮轨垂向力
由表6可知,动车组轮轨垂向力取决于车速,车速越大轮轨垂向力也越大。
3 雨棚结构振动响应
动车组交会通过雨棚时产生气动载荷和轮轨力,2种外部载荷对雨棚结构进行激励,分别将气动载荷施加在雨棚上,轮轨力作用在轨道板上,并进一步传递到雨棚结构上,主要分析雨棚的振动响应。
3.1 雨棚振动响应影响因素
为了分析不同外部载荷对雨棚振动响应的影响程度,以动车组350 km·h−1速度级在雨棚中部交会为例,分别计算气动载荷和轮轨力综合作用、气动载荷单独作用、轮轨力单独作用3种工况,得到雨棚振动响应结果见表7,其振动响应云图如图17所示。

表7 雨棚振动响应影响情况对比
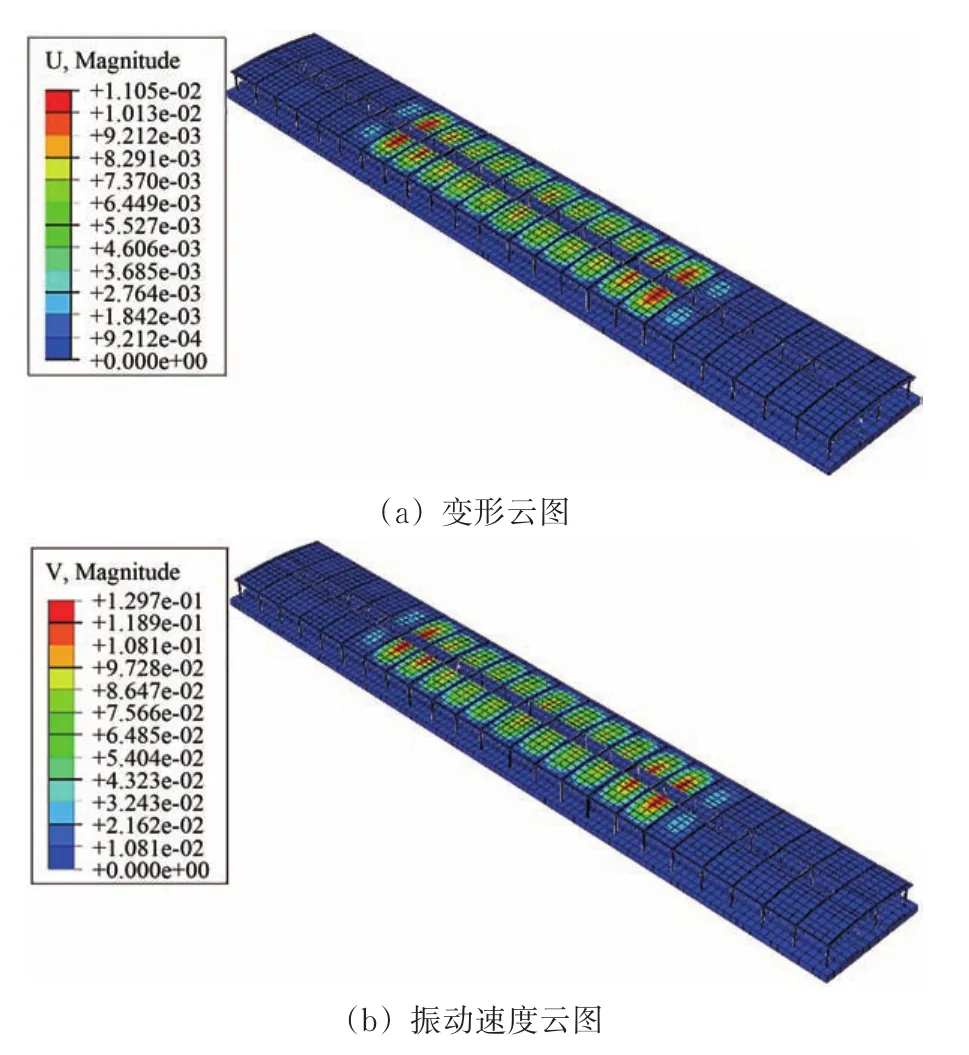
图17 雨棚振动响应云图
由表7和图17可知:气动载荷是引起雨棚振动响应的主要因素,轮轨力为次要因素,这主要由于气动载荷直接作用在雨棚上,且雨棚表面积相对较大,所以振动响应较大;轮轨力直接作用于钢轨,通过钢轨传递到轨道板并进一步传递到下部土体,再通过土体传递到雨棚支柱的底部基础,最后通过支柱传递到雨棚上部,传递过程较长,且下部通过土体传递,振动能量耗散较大,引起的雨棚振动响应相对较小。
3.2 雨棚振动响应规律
针对该雨棚特定结构,选择相对不利的位置进行分析,其中中间跨跨度最大,端部跨只有一侧有纵梁约束,另一侧没有纵梁连接约束且端部有延伸出的雨棚。动车组以不同速度级在上述2个不利位置交会时雨棚的振动响应极值见表8。以表8的数据为基础,拟合出动车组分别在雨棚中部和端部交会时的雨棚振动响应与车速关系如图18和图19所示。
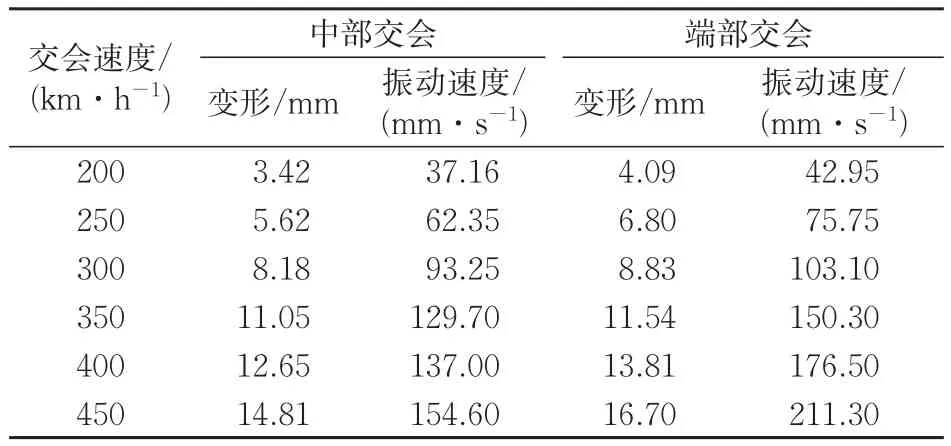
表8 动车组不同交会速度下雨棚振动响应极值
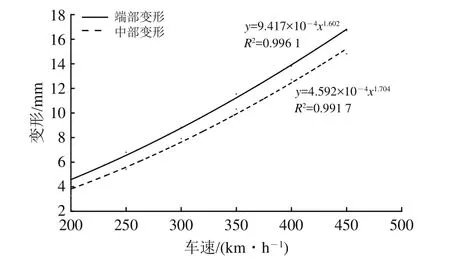
图18 雨棚变形与车速间关系

图19 雨棚振动速度与车速间关系
由表8及图18和图19可知:动车组以不同速度级等速交会时,雨棚的振动响应与车速有关,车速越大雨棚振动响应越大,其中端部交会时雨棚的变形与车速的1.60次方成正比,雨棚的振动速度与车速的1.88次方成正比,中部交会时雨棚的变形与车速的1.70次方成正比,雨棚的振动速度与车速的1.93次方成正比;同等速度级交会工况下,动车组在雨棚端部交会时雨棚的振动响应比动车组在雨棚中部交会时大,主要由于雨棚端部类似悬臂梁结构,其刚度相对于中间跨的刚度稍弱,因此,雨棚端部振动响应相对较大。
目前国内尚未发布专门针对雨棚结构振动限值的相关标准,根据《建筑工程容许振动标准》(GB 50868—2013)[19]规定,建筑物顶层楼面中心位置处水平2个主轴方向的振动速度峰值为10 mm·s−1。但本文研究的雨棚振动主要以垂向振动为主,后期会对雨棚垂向振动标准限值进行进一步研究。
4 结 论
(1)当CR400AF型动车组以不同速度在雨棚中部等速交会时,雨棚靠近线路中心位置处所受的气动载荷最大,雨棚宽度、长度方向所受气动载荷近似于呈对称分布,气动载荷随着雨棚高度的增加而减小。
(2)当CR400AF型动车组以不同速度等速交会时,雨棚所受的气动载荷约与车速的平方成正比;雨棚的振动响应也约与车速的平方成正比,车速越大振动响应越大。
(3)CR400AF型动车组在同等速度级交会工况下,雨棚的振动响应端部比中部大,而且振动响应较大值出现在两端车头和车尾所在位置。
(4)气动载荷和轮轨力对雨棚振动响应的影响程度不同,相对而言,气动载荷对雨棚振动响应起主要作用。
