基于多目标优化的高速铁路车辆-轨道-桥梁空间耦合系统模型修正研究
2022-06-09姜涵文
高 亮,姜涵文
(北京交通大学 土木工程学院,北京 100044)
随着我国高速铁路的迅速发展,列车运行速度不断提高并且高铁网总里程逐年增加,对列车运行的平稳性、安全性和可靠性提出了更高的要求,而轨道结构作为列车运行的载体,其服役状态对列车运行产生重要影响。目前大量学者及研究人员对轨道结构的服役状态研究主要依赖仿真方法,但是由于材料参数取值的随机性和离散性、模态频率误差及仿真模型不合理简化等,均会使得仿真模型与实际结构产生不可避免的误差,对仿真结果的准确性造成影响[1]。因此,有必要基于实测数据对仿真模型进行模型修正研究以提高仿真结果的准确性,这将对高速铁路轨道结构设计及服役状态研究具有重要意义。
近年来,国内外学者对模型修正在铁路基础结构领域的应用进行了一些研究。方兴[2]基于动力优化与静力效应组合对铁路钢桁梁桥有限元模型进行了模型修正;骆勇鹏等[3]基于逐步回归分析的有限元模型修正方法对一既有铁路钢桁桥的有限元模型进行修正,并与基于灵敏度的模型修正方法进行比较;战家旺等[4]基于有限元模型修正理论,用模态频率残差和模态振型残差构造目标函数,实现对桥墩损伤的定位和定量评估;Feng等[5]根据现场实测的铁路桥梁动位移时程数据对有限元模型进行了模型修正研究;Malveiro等[6]基于现场模态测试对铁路钢混桥进行了模型修正,并且评估了修正后模型的动力响应;Xia等[7]提出了一种粒子群优化和响应面法相结合的铁路桥梁模型修正方法并且采用梁模型对该方法的有效性进行了测试。可见,目前关于铁路基础结构的模型修正研究基本聚焦于桥梁结构,而对于轨道结构的模型修正研究鲜有提及。
本文以高速铁路桥上CRTSⅡ型板式无砟轨道为模型修正对象,建立车辆-轨道-桥梁空间耦合系统模型,基于现场实测的轴箱加速度和仿真结果初步验证模型的可靠性并建立多目标模型修正函数,采用拉丁超立方方法进行灵敏度分析以获得待修正的参数,采用多岛遗传算法对多目标函数进行全局寻优以完成模型修正过程。
1 车辆-轨道-桥梁空间耦合系统仿真模型
车辆-轨道-桥梁空间耦合系统模型包括车辆模型和轨道-桥梁模型,车辆与轨道-桥梁之间的耦合通过轮轨相互作用实现。
1.1 车辆模型
车辆模型以CRH380B型动车组车头为原型,基于多体动力学理论将车辆模型考虑成多刚体结构。模型包括1个车体、2个转向架及4个轮对,各部件之间通过一系和二系悬挂连接,车辆模型示意图如图1所示。悬挂系统考虑其非线性,采用弹簧阻尼结构进行模拟,其中每个部件均考虑6个自由度(浮沉、横移、伸缩、点头、摇头和侧滚),模型共计42个自由度。
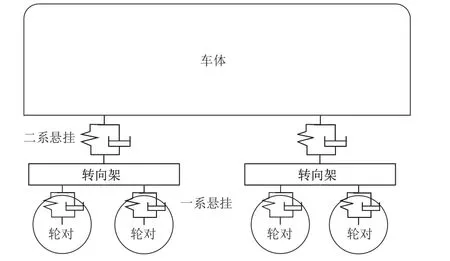
图1 车辆模型示意图
车辆模型的运动方程为

式中:MV,CV和KV分别为车辆模型的质量、阻尼和刚度矩阵;和δV分别为车辆模型的加速度、速度和位移向量;FV为车辆所受的外力向量。
车辆的相关参数取值见文献[8]。
1.2 轨道-桥梁模型
轨道-桥梁模型由2部分组成,分别为CRTSⅡ型板式无砟轨道和桥梁,如图2所示。

图2 轨道-桥梁模型
轨道结构包括钢轨、扣件、轨道板、CA砂浆层和底座板。桥梁结构包括1跨32 m箱梁和桥梁支座,并且钢轨向前延伸100个扣件长度以消除列车运行时模型边界条件等因素的影响。为了能够真实地反映结构的物理和几何特性,除了扣件和桥梁支座采用弹簧-阻尼单元外,其余部件均采用实体单元模拟。轨道-桥梁模型的运动方程为
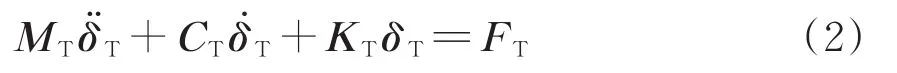
式中:MT,CT和KT分别为轨道-桥梁模型的质量、阻尼和刚度矩阵;和δT分别为轨道-桥梁模型的加速度、速度和位移向量;FT为轨道-桥梁模型所受的外力向量。
轨道-桥梁模型采用60 kg·m−1钢轨,扣件间距为0.65 m,轨底坡设置为1∶40,轨道-桥梁模型的材料参数取值见文献[9]。
1.3 轮轨相互作用和轨道不平顺
车辆模型与轨道-桥梁模型之间的耦合关系通过轮轨相互作用实现,轮轨相互作用的确定分为2个步骤,首先需要确定轮轨接触点位置,然后根据确定的接触点位置确定轮轨相互作用力。
首先假定刚体轮对与柔性体钢轨仅存在1个接触对,然后将轮轨廓形采用三尺样条曲线进行插值离散,最后通过轮轨的侧向位移即可得到轮轨的接触斑进而确定轮轨接触区域;轮轨接触点位置确定后,根据Hertz非线性弹性接触理论[10]进行轮轨法向力求解,采用FASTSIM算法[11]对轮轨切向力进行求解。
轨道不平顺采用开展轴箱加速度测试的实测轨道不平顺。
1.4 仿真模型验证
为保证模型修正研究的可行性,需要对建立模型的可靠性进行验证。将仿真模型计算的轴箱加速度结果与实测结果(数据经过去零漂、剔除坏值、去除噪声等处理)进行对比,仿真模型的运行工况与测试工况一致,实测和仿真得到的轴箱加速度时程如图3所示。
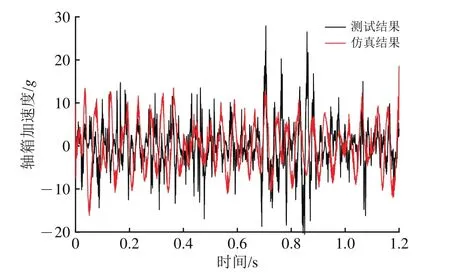
图3 轴箱加速度仿真结果和实测结果
从图3可以看出:轴箱加速度的仿真结果与实测结果的波动线形及数量级基本一致,表明本文建立的仿真模型能够较为准确地反映出轴箱加速度在时域上的振动特性,模型可靠性。
2 模型修正研究
由模型验证可见,尽管仿真结果与实测结果相似度较高,但是仍存在一定的差异。造成差异的原因主要有材料参数取值的随机性和离散性,模态频率误差,仿真模型不合理的简化等。因此需要采用模型修正技术对模型的参数进行修正,以提高仿真结果的准确性。
2.1 模型修正多目标函数

2.2 模型参数灵敏度分析
灵敏度分析是为了选取对模型修正函数影响较大的参数,能够缩小参数设计空间并提高修正效率。实验设计(DOE)是目前开展灵敏度分析最广泛采用的方法,实验设计包含很多方法,并且每种方法都有自己的特点。考虑到拉丁超立方方法具有2大优点:①选取的样本点能够有效地充填整个空间;②更好地拟合非线性响应[13]。因此本文采用拉丁超立方方法进行灵敏度分析。
根据车辆-轨道耦合动力学理论[14−15],选取钢轨、轨道板、CA砂浆、底座板、桥梁的密度和弹性模量及扣件刚度共11个参数进行灵敏度分析,各参数的修正范围见表1。
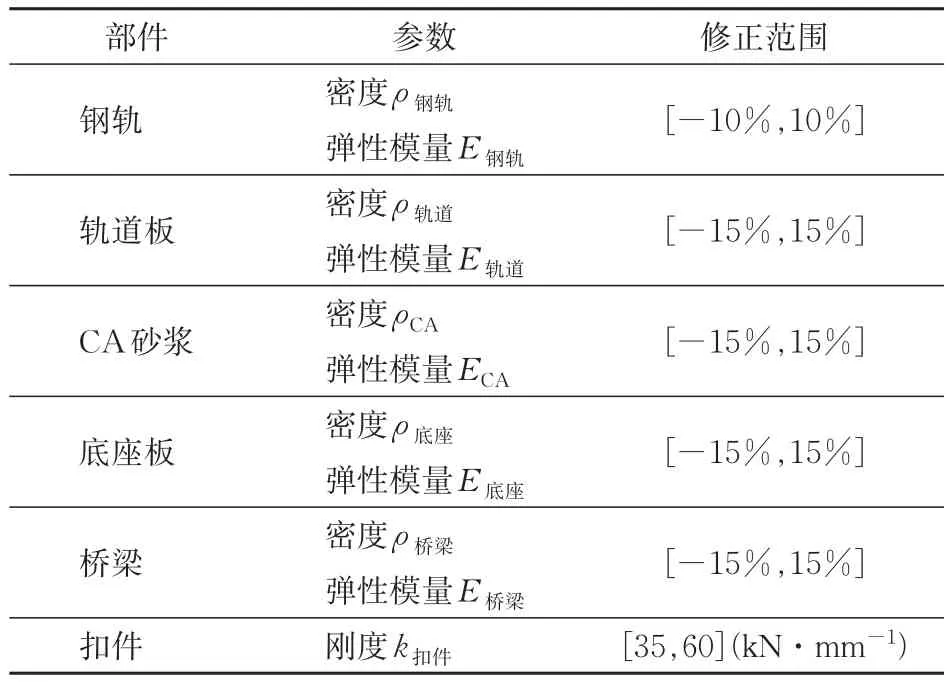
表1 灵敏度分析的模型参数及修正范围
首先采用拉丁超立方方法对选取的参数在给定的修正范围内进行抽样,将抽取到的样本输入到仿真模型中进行轴箱加速度计算,然后基于仿真结果进行目标函数的评价,最后根据各参数对目标函数的影响程度绘制得到Pareto图,如图4所示。图中:影响程度为负,表示目标函数随该参数的增大而减小;影响程度为正,表示目标函数随该参数增大而增大。
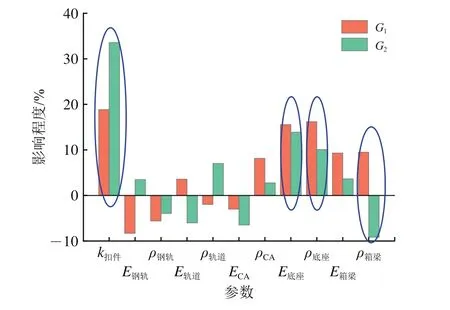
图4 灵敏度分析Pareto图
从图4可见:各参数对目标函数的影响程度有正有负且在数值上存在明显差异;扣件刚度对2个目标函数均有最显著影响,也就是说扣件刚度是影响轴箱加速度的主要因素;除扣件刚度外,底座板的密度和弹性模量以及桥梁的密度对2个目标函数均产生较大影响,且影响程度均大于9%。
根据灵敏度分析结果,最终选取扣件刚度k扣件、底座板密度ρ底座、底座板弹性模量E底座、桥梁密度ρ桥梁4项参数作为待修正的模型参数。
2.3 模型修正
根据灵敏度分析选取得到的待修正参数,进行模型修正。此类优化问题可以采用遗传算法(GA)进行求解,该算法是1种基于自然选择理论的启发式算法,寻优过程依靠生物启发算子,例如变异、交叉、选择等[16]。虽然遗传算法已经广泛应用于全局寻优问题,但是容易陷入局部最优解和出现早熟现象,所以在遗传算法的基础上发展出一些可以克服该问题的算法,其中多岛遗传算法(MIGA)既能避免前述问题的出现又保留了遗传算法的优势[17]。多岛遗传算法的最大改进就是将种群分成若干子种群即“岛”,每个岛中的部分个体在满足迁移间隔时会进行迁移操作。在岛与岛之间进行的迁移操作能够提高种群的多样性、避免早熟并且会防止局部最优解的出现[18−20]。因此,本文选择多岛遗传算法进行模型修正过程的求解,详细的修正流程如图5所示。
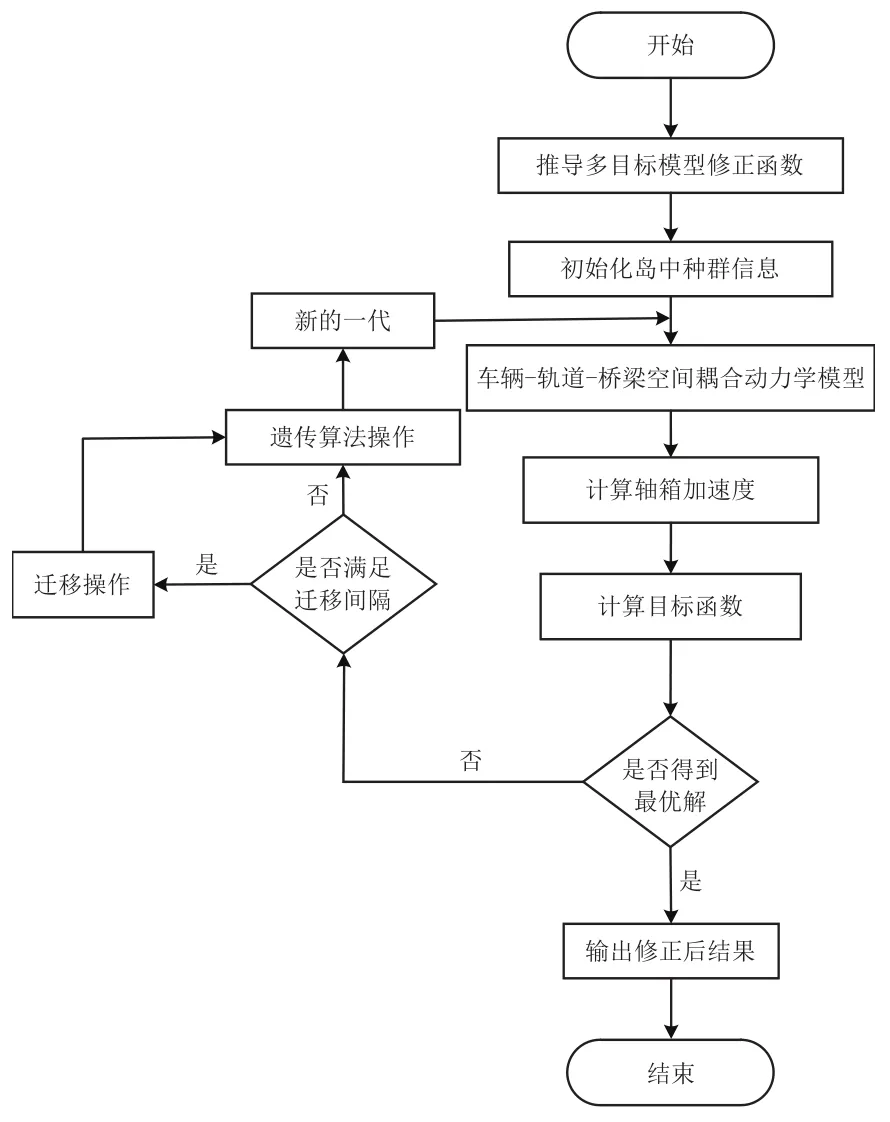
图5 模型修正流程图
多目标优化与单目标优化本质上存在差异,因为多目标优化的目标函数之间相互牵制,所以不存在唯一的全局最优解[21],而是存在最优解的集合,该集合被称为Pareto最优解集,集合内的元素对应的至少一个目标函数优于其他所有的解,数学表述为:在n维解空间Ω内,对于任意解Ai,当且仅当∄Aj∋Ω,使得g(Aj)优于g(Ai),则Ai为Ω内的Pa⁃reto最优解。Pareto最优解集中的元素对应的目标函数值所构成的曲线称为Pareto前沿。
在模型修正过程中,设置岛屿数量为10,子种群规模为10,迁移间隔为5,经过241次迭代,得到的Pareto前沿如图6所示。
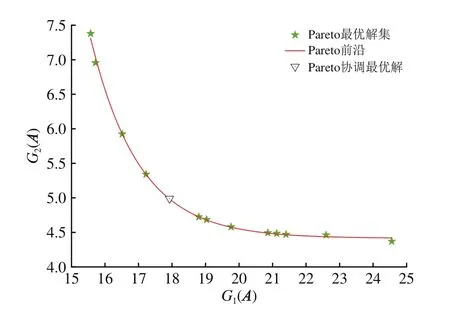
图6 Pareto前沿
由图6可见,Pareto前沿上的最凸点明显,所以得到了一个较好的协调最优解。
该解对应的修正后参数与初始参数之间的对比见表2。
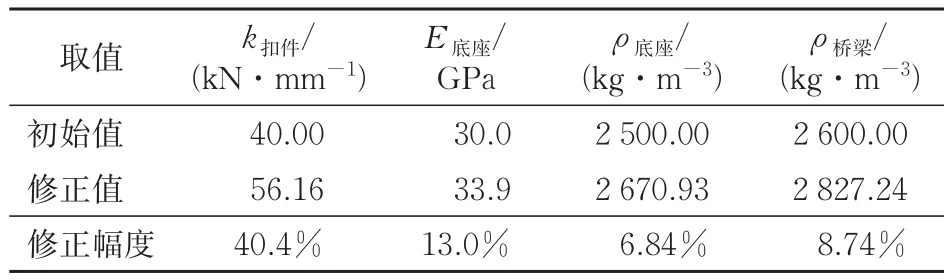
表2 修正前后参数对比
从表2可以看出:扣件刚度的修正幅度高达40.4%,这主要是因为仿真模型中扣件刚度的取值多依赖于静力试验的结果,而实际运营条件下扣件的动刚度与静刚度间存在较大的差异,所以仿真模型中对于扣件刚度初始值的确定具有一定的难度;修正后的底座板密度、弹性模量及桥梁密度均较初始值有一定的增大,这主要是由于混凝土材料本身的离散性及混凝土内配有钢筋造成的。
修正前后的轴箱加速度仿真结果与实测结果之间的对比如图7所示。
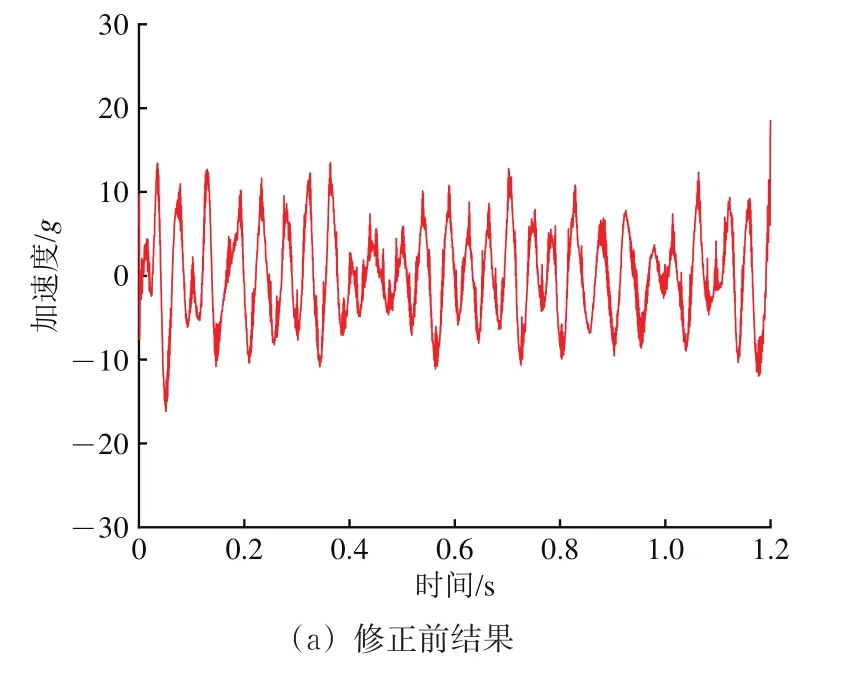

图7 模型修正前后轴箱加速度仿真结果与测试结果对比
由图7可以看出:在时域分布线形及数值大小方面,修正之后的轴向加速度与实测结果间具有更高的一致性,并且协调最优解对应的目标函数G1(A)和G2(A)相较于初始值分别减小了26.6%和34.2%。
综上所述,修正后的模型参数均处于合理的范围内,并且仿真结果的准确性有明显提高,因此表明了本文提出的模型修正方法的有效性。
3 模型修正有效性评估
通过仿真模型得到的轨道和桥梁结构动态响应与文献[22]的实测结果进行对比分析进行修正后模型的有效性评估。动态响应指标包括钢轨垂向位移和钢轨、轨道板及桥梁的垂向加速度,由于文献[22]中测试时的车辆、轨道及桥梁型式均与本文建立的模型相同,所以进行对比应该是合理有效的。
修正后模型计算得到的轨道和桥梁结构动态响应时域曲线如8所示。
由图8可见:钢轨位移呈马鞍形分布,且当列车4个轮对经过时达到峰值,钢轨位移最大可达1.00 mm;钢轨、轨道板和桥梁加速度是明显的波动-衰减过程,当列车经过时波动达到最大,分别为145.3g,3.97g和0.211g,当列车驶离时出现衰减现象。

图8 轨道和桥梁结构动态响应时程曲线
表3给出了修正后模型的仿真结果与实测结果的对比。
由表3可知:修正后模型的仿真结果与实测结果较好地吻合,说明修正后的模型不仅能够准确地仿真轴箱加速度的时域分布特征,又能准确模拟轨道结构的动力响应,进一步证明了本文提出的模型修正方法的可行性。
4 结 论
(1)根据实测轴箱加速度和仿真结果的对比分析,初步验证了仿真模型的可靠性,并且也进一步证明了采用该模型进行灵敏度分析和模型修正的可行性。
(2)采用拉丁超立方采样方法进行了灵敏度分析,分析结果表明目标函数对于扣件刚度k扣件、底座板密度ρ底座和弹性模量E底座、桥梁密度ρ桥梁更加敏感。基于此,最终选取上述4个参数进行模型修正。
(3)采用多岛遗传算法进行了模型修正,得到了修正参数的Pareto前沿,利用最凸点法得到了Pareto协调最优解。修正后的轴箱加速度在时域分布线形及数值大小方面与实测结果具有更高的一致性,并且目标函数较修正前减小了26.6%和34.2%。
(4)对修正后模型得到的轨道动态响应与实测结果进行了对比分析,动态响应包括钢轨垂向位移和钢轨、轨道板及桥梁的垂向加速度,结果表明修正后模型的仿真结果与实测结果有很好的一致性。
