基于DEM-MBD耦合方法的路桥过渡段不均匀沉降研究

陈 成，罗启天，杨 超，芮 瑞，王晓壮

（1.武汉理工大学 土木工程与建筑学院，湖北 武汉 430070；2.同济大学 中国交通研究院，上海 200092）

受地理环境的影响，高速铁路建设不可避免地会遇到不同轨下基础连接处的过渡段，这些地段往往是高速铁路线路的薄弱环节。路桥过渡段位于普通路基与桥梁刚性路基之间，且桥梁处的刚度远大于普通路基结构处。由于过渡段两侧较大的刚度差必然引起路基产生相应的不均匀沉降，进而降低列车运行的平顺性，加剧过渡段处线路的劣化，从而导致轨面发生弯折、轨枕空吊与轨枕断裂等铁路灾害，因此针对路桥过渡段维护方面往往需要耗费大量的人力物力以保证列车行车安全。

近年来针对铁路过渡段问题，国内外学者开展了一系列的研究工作。在试验研究方面，Li等[1]在同1条铁路线路上针对4处路桥过渡段进行沉降监测，发现过渡段处轨枕的平均沉降比其两侧路基处轨枕更大，并指出可以通过在刚度较低的路基结构处铺设混凝土板、土工格栅减少刚度差异产生的不均匀沉降；练松良等[2]建立了铁路过渡段局部模型并进行压载实验，发现使用道砟垫可以有效调整轨道整体刚度，使桥上与路基上轨道的整体刚度平顺过渡，减少突变；Boler等[3]结合实际工程采用吹石法替代道砟捣鼓，研究发现吹石法可以有效解决路桥过渡段处的差异沉降；Yu等[4]在某大型沥青混合有砟轨道上进行了变刚度路基的阶段性荷载循环压载试验，研究了路桥过渡段铺设沥青轨道后的长期沉降特性，结果表明沥青层可以保护路基不受高应力的影响，减小轨道沉降。在数值模拟方面，雷晓燕等[5]通过建立列车-轨道-路基耦合动力分析模型，考虑列车速度、路基刚度以及轨道不平顺等因素研究了过渡段动力特性，发现过渡段路基刚度突变对钢轨垂向加速度和轮轨作用力均有影响；Chen等[6]采用改变路基墙单元的刚度的方法建立离散元多轨枕过渡段简化模型，研究了过渡段的劣化机理以及土工格栅的加固效果；Li等[7]借助有限-无限元模拟方法，研究了变长与定长碎石桩加固下路桥过渡段动力特性，结果表明采用长桩加固软土路基后，桥梁附近的桩承受更大的动力荷载，路桥过渡段的刚度得到了平滑的过渡。文献[8—12]基于有限元数值模拟方法，研究了铁路过渡段在各因素下劣化沉降情况。

综上所述，由于实际铁路路桥过渡段尺寸过大，模型试验较少，主要以现场监测研究为主。数值模拟研究主要是基于有限元的铁路道床整体分析或基于多体动力学方法分析道床上方轮轨接触关系，无法分析过渡段道床的细观力学行为特征。本文针对当前研究的不足，采用离散元（Discrete Element Method，DEM）与多体动力学（Multibody Dynamics，MBD）耦合的方法建立轨枕-道砟-路基过渡段耦合模型，从细观力学机理角度研究过渡段劣化规律。通过不同路基刚度分布形式、行车速度、列车轴重以及桩基加固措施下过渡段不均匀沉降分析，研究影响路桥过渡段沉降劣化机理以及桩基加固效果。为铁路路桥过渡段的养护维修以及状态评估提供参考。

1 过渡段DEM-MBD耦合数值模拟

1.1 过渡段DEM-MBD模型

实际工程中铁路路桥过渡段一般在20 m左右，考虑到颗粒流离散元方法的运算效率及限制，基于离散单元法对路桥过渡段进行全尺寸模拟是不切实际的。因此为了研究路桥过渡段不均匀沉降的细观机理，参照文献[6]的3个轨枕简化模型，采用远置边界的方法建立路桥过渡段简化的6、9和12个轨枕路桥过渡段模型，验算结果显示3个模型的沉降偏差小于10%。为方便本文选取6个轨枕的路桥过渡段模型，如图1所示。路桥过渡段共分为普通路基区、过渡路基区与桥面路基区3个区，其中1#和2#，3#和4#，5#和6#轨枕分别在普通路基区、过渡路基区和桥面路基区内，各路基区沉降为该路基区所有轨枕的平均沉降。

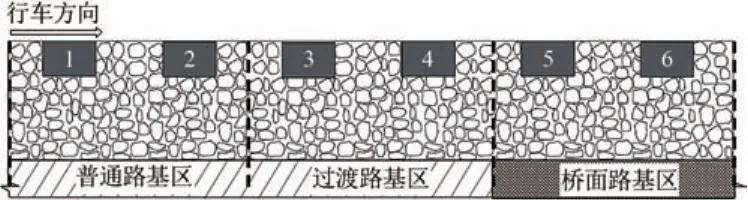
图1 路桥过渡段示意图

使用离散元软件EDEM与多体动力学软件Re⁃curDyn，建立轨枕-道砟-路基过渡段耦合模型，如图2所示。在建立“轨枕-道砟的离散元模型时，轨枕的长、宽和高分别取280，300和150 mm，放置于长、宽和高分别为3 600，300和500 mm的道砟箱中，道砟层厚度350 mm，轨枕间距取600 mm。在道砟颗粒构建时，尽管采用多个球组成道砟颗粒可以更好地体现各种道砟颗粒的棱角度等特征，然而已有研究[6，13−15]也表明，简化颗粒虽然低估了真实道砟的咬合作用，但对道砟的细观力学特征体现相近，因此采用双球clump可以较好地模拟道砟的力学性能，考虑到离散元计算效率，本文采取简化外形的双球颗粒簇充填道床，如图3所示。建立道床模型时，采用落雨法对道床模型进行充填并进行分层压实以保证道床密实度符合规范。在参数的选取上参照Chen等[6]和郑瑶等[16]的研究，并通过改变模型各细观参数进行大量模拟尝试，最终确定模型各细观参数，具体见表1。

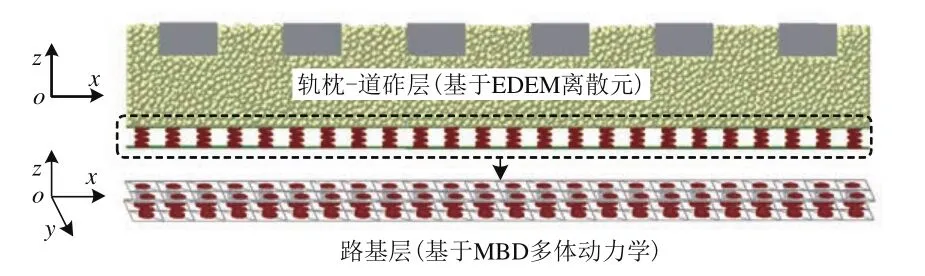
图2 轨枕-道砟-路基过渡段耦合模型

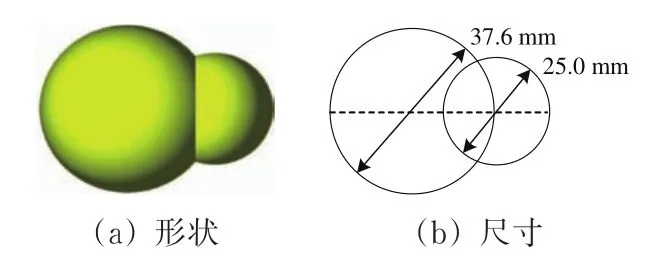
图3 离散元道砟颗粒模型

表1 模型细观参数取值

文科勒弹性路基模型是将路基作为弹性介质进行处理的方法[17]。该方法假定路基由许多独立且互不影响的弹簧组成，即路基表面某点所受压强与该点的沉降量成正比，与其他点的压力无关。基于该假定，Chen等[6]通过改变用于模拟路基刚性墙的刚度值的方法实现对不同刚度路基的模拟，但是该方法采用的刚性墙与道砟颗粒的重叠量极小，无法较好模拟路基受力沉降变形的特性。因此本文基于DEM-MBD耦合方法，建立了48个相互独立的弹簧组成的路基模型，如图2所示。参考Chen等[6]前期研究，过渡段模型中软、硬路基的弹性模量分别取25和100 MPa。根据Tomlinson法[17]，荷载作用下半无限均匀线弹性路基的沉降为

式中：s为刚性基础在半无限均匀线弹性基处上的沉降，m；q为加载压力，N·m−2；E为弹性模量，Pa；B为方形板的边长，m；v为路基泊松比，选取0.2；I为影响系数，选取0.8。

本模拟中文科勒弹性路基的弹簧刚度通过压载标定，如图4所示。已知对平板施加的荷载q，先根据式（1）计算软路基和硬路基的沉降，再由胡克定律计算可得软路基处弹簧刚度为4.9 MN·m−1，硬路基处弹簧刚度为20 MN·m−1。

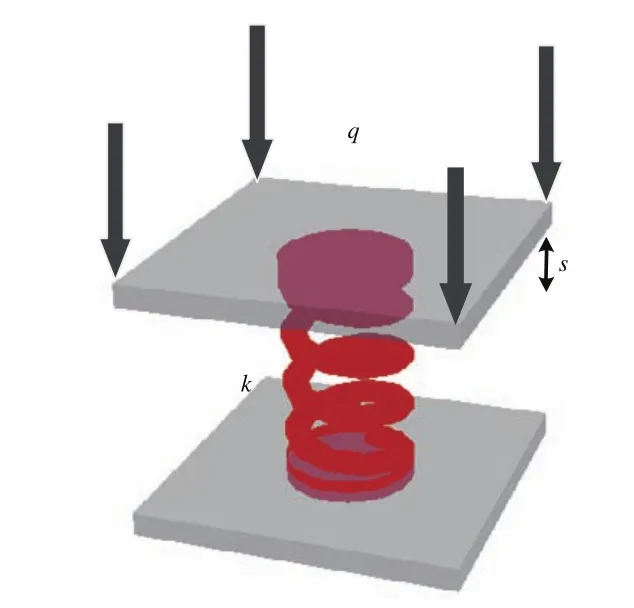
图4 文科勒路基弹簧刚度压载标定

图5为DEM-MBD耦合流程示意图，具体的耦合流程为：在1个循环耦合步内，MBD先进行1个时间步长计算并将位移数据通过耦合接口传递到DEM中，随后DEM计算颗粒与几何体相互作用情况，再将力与力矩传回MBD中，MBD根据DEM传回的数据重新计算几何体位移信息。需要说明的是在耦合计算中DEM与MBD中时间步长是成倍数关系的，其中DEM需要更小的时间步长以保证模拟的收敛。

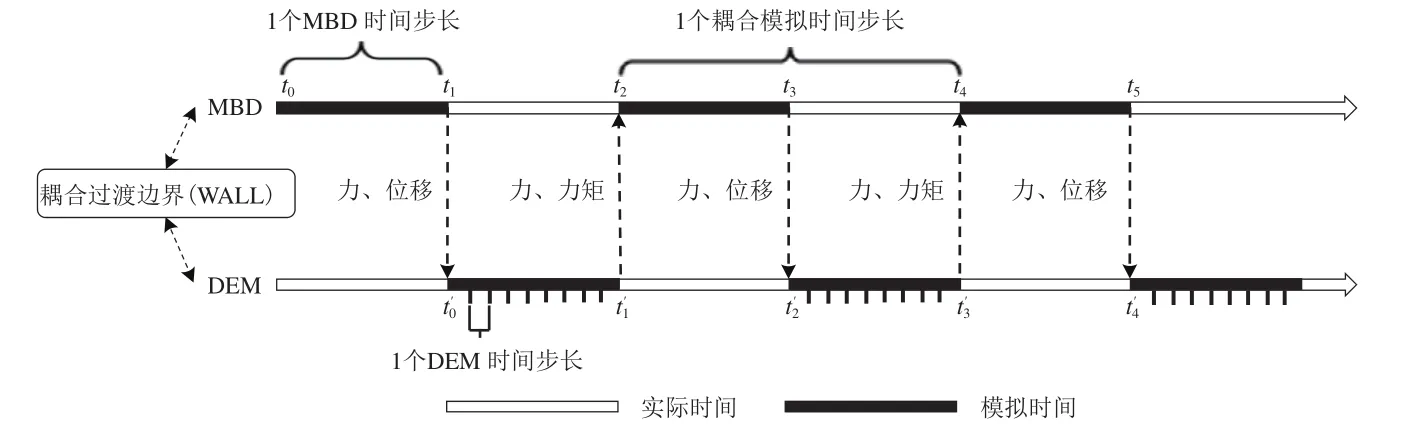
图5 DEM-MBD耦合流程示意图

1.2 行车荷载的实现

Awoleye[18]首先提出了通过对每根轨枕施加90°相位差的移相正弦荷载模拟列车荷载。本文采用该加载模式对各轨枕施加最大值为40 kN的90°相位差正弦荷载。

图6为将道砟颗粒间接触力数据导入Python进行处理后，模型在移相正弦荷载下1个循环内的道砟层应力链分布图。图中线条的粗细反映接触力的大小；i=0，1，2，…，n-1，n为循环次数；T为周期。由图6可以很清楚地观察到，各轨枕下方道砟层应力链均是周期性的增大和减小，与实际列车行经轨枕时轨枕受力变化趋势一致，因此采用90°移相正弦荷载的加载方式模拟行车荷载是可行的。

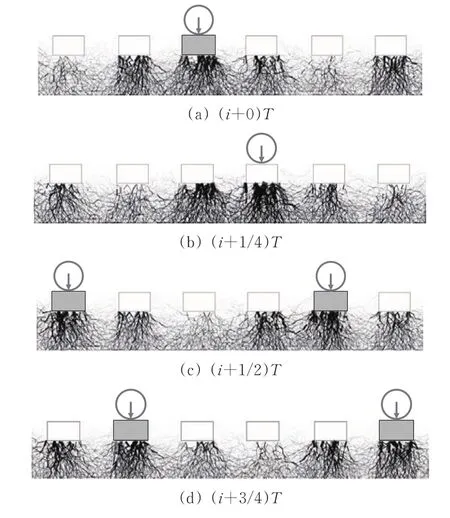
图6 不同加载时刻道砟层应力链分布

1.3 模型验证

为了验证路桥过渡段模型和加载方式的可靠性，首先分析当模型中路基均为硬路基时各轨枕的沉降情况。图7为在90°移相正弦荷载作用下，均一路基刚度时各轨枕的沉降情况。由于道床填充、压实过程的随机性，各轨枕之间沉降值虽有细微差异，但可认为一致。

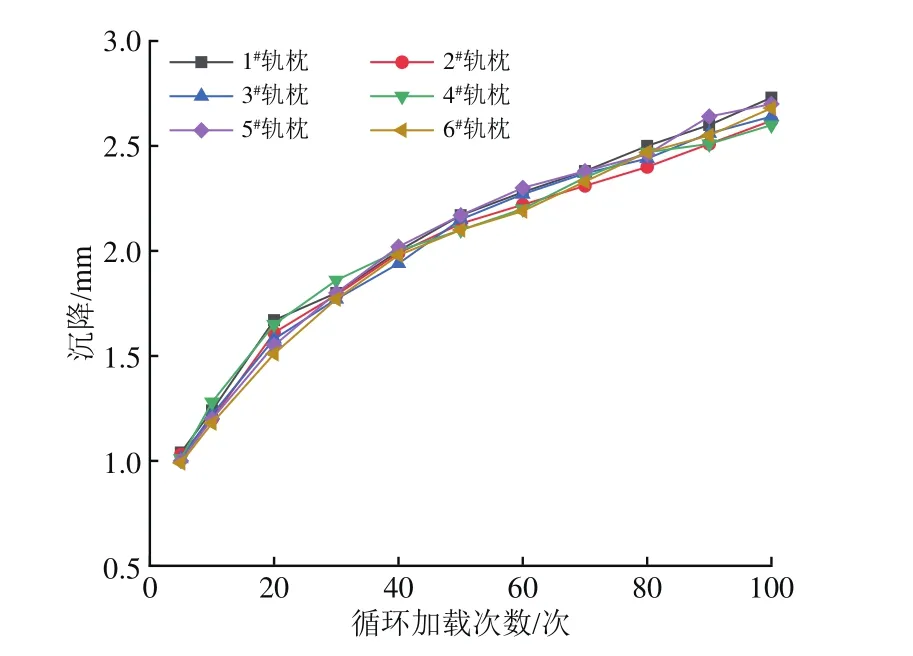
图7 均一路基刚度（硬路基）下各轨枕沉降

Li等[1]在研究过渡段沉降时的试验数据表明，路桥过渡段中过渡路基区的沉降均大于其两侧的普通路基区与桥面路基区的沉降。本节设过渡段模型软路基段（普通路基区、过渡路基区）刚度为4.9 MN·m−1、硬路基段（桥面路基区）刚度为20 MN·m−1，图8为过渡段模型在100次循环加载后各路基区沉降，图9为Li等[1]监测路桥过渡段线路历经1个维护周期后各路基区沉降。由图8和图9可以看出：过渡段不均匀沉降的模拟结果和实测数据趋势一致，均为过渡路基区轨枕沉降最大，普通路基区次之，桥面路基区最小。由于Li等[1]现场实测数据是过渡段经历1个维护周期后的结果，因此现场实测值相较本文模拟结果更大。因此，本模型用于研究路桥过渡段的不均匀沉降是可行的，后续将基于该模型进行过渡段的影响因素分析。

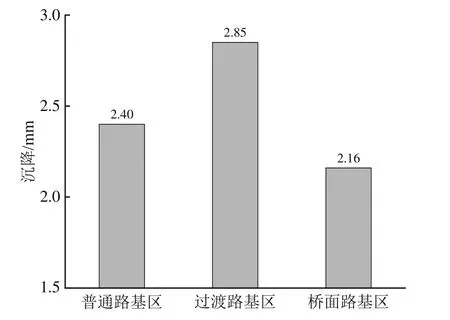
图8 过渡段各路基区沉降耦合模拟结果

图9 过渡段各路基区沉降实测数据[1]

2 路桥过渡段不均匀沉降

2.1 不同路基刚度的影响

在实际工程中可以采用过渡段搭板法以减小路桥过渡段两侧结构刚度差异，通常做法是，在临近桥梁的过渡路基区范围内路堤填料上浇筑钢筋混凝土厚板，并使一端支撑在刚性基础（桥台）上。大多数混凝土板在接近桥墩方向厚度是逐渐增大的（即逐渐增大该区域路基刚度），或者采用厚度均匀且以一定倾角放置混凝土板，通过利用厚板的抗弯刚度增加过渡路基区的整体刚度。Selig等[19]研究表明路基刚度大小对铁路沉降有重要影响。为了研究路基刚度的分布形式对路桥过渡段沉降劣化的影响，建立2种过渡段路基模型：模型A，路基刚度突变型（未加固）；模型B，路基刚度渐变型（搭板法加固）。对于模型B，道床下方路基刚度由软路基到硬路基逐渐从4.9 MN·m−1增大至20 MN·m−1，同时相应路基弹簧上方路基与道砟摩擦系数相应由0.2逐渐增大至0.6，该模型代表软路基处经过渡段搭板法加固后的过渡段区域。

图10为100次循环加载后2种过渡段模型中各路基区的轨枕沉降。由图10可以看出：2种模型均表现为过渡路基区的轨枕沉降最大、桥面路基区的轨枕沉降最小；模型A过渡段的不均匀沉降为0.69 mm，模型B过渡段的不均匀沉降为0.3 mm，比模型A减小约56.5%。

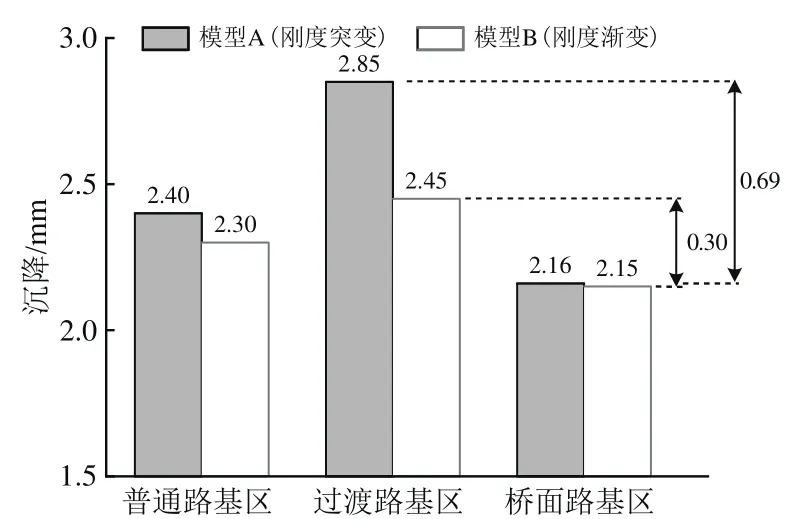
图10 100次循环加载后2种过渡段各路基区的轨枕沉降

为更好地量化分析2种模型中道床沉降情况，通过在EDEM中提取模型中过渡路基区道砟颗粒与颗粒间的接触力信息（图11），得到图11所示2种过渡段模型中过渡路基区的道砟接触力在各方向上分布的玫瑰云图，图中长度表示该区间的平均接触力。由图12可以看出：采取刚度渐变加固措施的模型B中过渡路基区道砟间的平均接触力明显小于路基刚度突变的模型A。这是由于在荷载作用下，模型A中路基刚度在过渡路基区与桥面路基区的连接处发生突变导致道砟颗粒间发生错落滑动，使得沉降大多发生在刚度突变处（即过渡路基区），而模型B中采用路基刚度逐渐增大可以使得路基上方道砟颗粒在列车荷载作用下相互咬合更加紧密和稳定，从而有效地降低路桥过渡段整体的不均匀沉降，验证了实际工程中在临近桥梁的过渡路基区路基中铺设混凝土板进行加固的可行性。

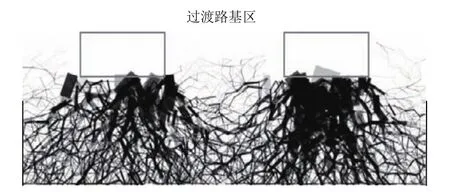
图11 过渡路基区中道砟接触力链范围

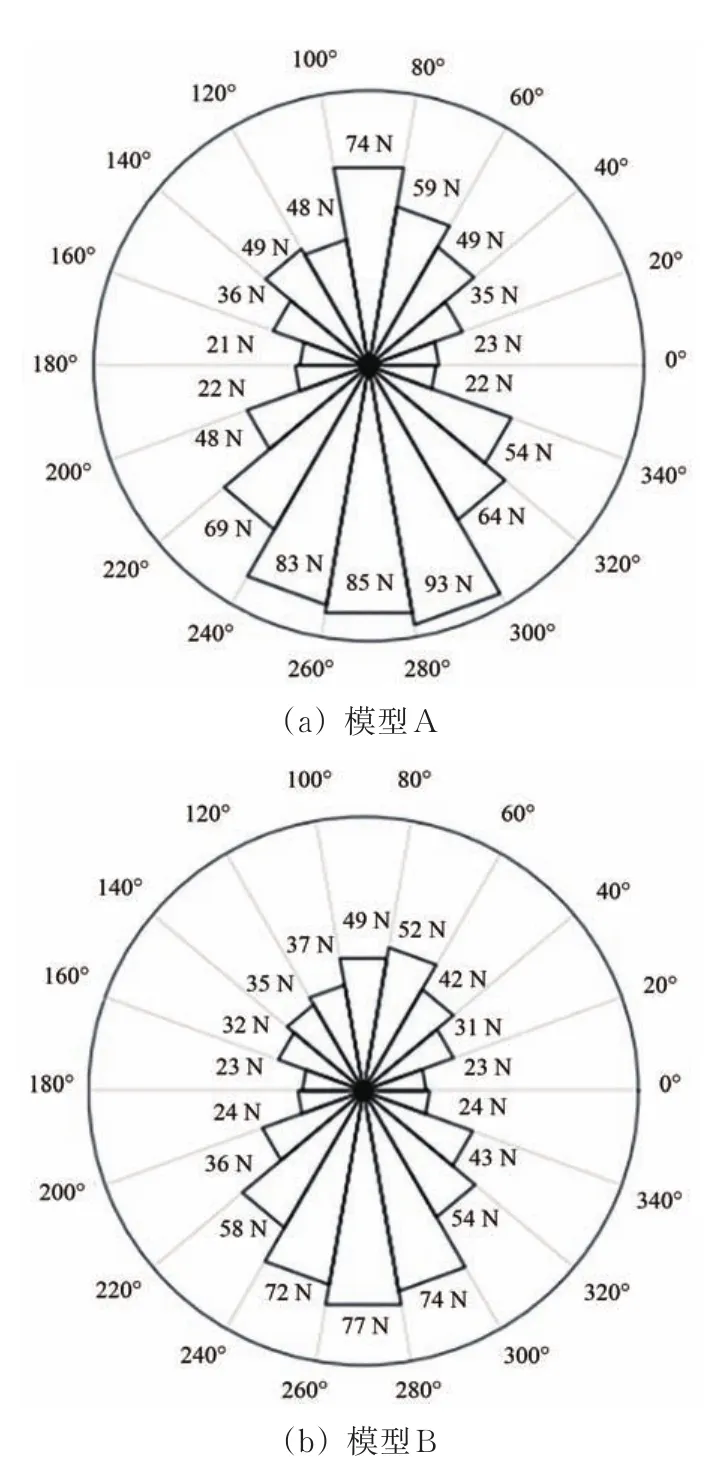
图12 2种路桥过渡段模型中过渡路基区道砟颗粒间接触力分布玫瑰云图

2.2 列车速度的影响

采用90°移相正弦荷载模拟行车荷载，其中荷载频率3，10，20和30 Hz分别代表28，94，187和281 km·h−1的列车速度。需要指出的是本文假设列车匀速水平前进，不考虑因轨道不平顺引起的列车荷载的改变。图13为在不同行车速度下2种过渡段模型各路基区的沉降。由图13可以看出：过渡路基区的沉降始终最大，并且不均匀沉降随着车速的提升而增大；在车速小于100 km·h−1时过渡段各路基区的沉降均随着车速提升而减小，当车速大于100 km·h−1时，过渡段各路基区的沉降随车速的提升明显增大；相较于模型A，模型B中不均匀沉降随着车速提升的幅值明显变小，且各路基区沉降同样明显小于模型A。因此列车车速的提升会加剧路桥过渡段的不均匀沉降，对过渡段的软路基采取刚度逐渐增大的设计可以有效减小因行车速度提升而导致的过渡段不均匀沉降，同时也验证了混凝土搭板法加固措施的有效性。

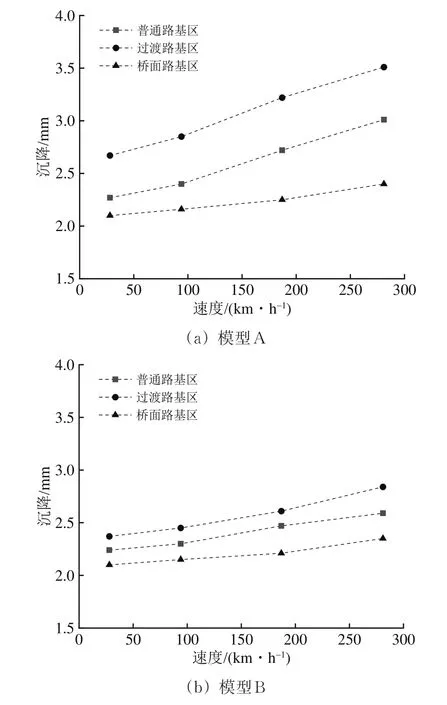
图13 不同车速下2种过渡段模型中各路基区的沉降

2.3 列车轴重的影响

本文模拟选取了16，24和32 t共3种轴重，研究不同列车轴重对路桥过渡段不均匀沉降的影响。图14给出了在不同轴重列车荷载作用下，100次循环加载后过渡段各路基区的沉降。由图14可以看出：路桥过渡段各路基区沉降随着列车轴重由16 t提升至24和32 t后，不均匀沉降由0.69 mm增大到1.15和2.48 mm，沉降呈倍数增长。图15为不同列车轴重下过渡段道床力链图。由图15可以发现：随着列车轴重的增大，道砟颗粒间的接触力增加明显，颗粒间咬合更为紧密，道床被进一步压实至更高应力水平。

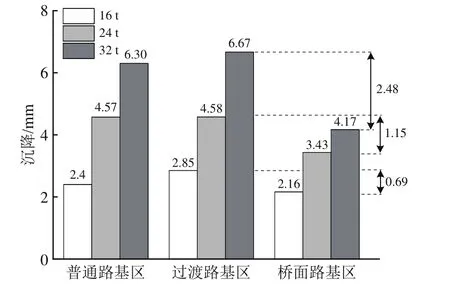
图14 不同轴重下过渡段各路基区的沉降

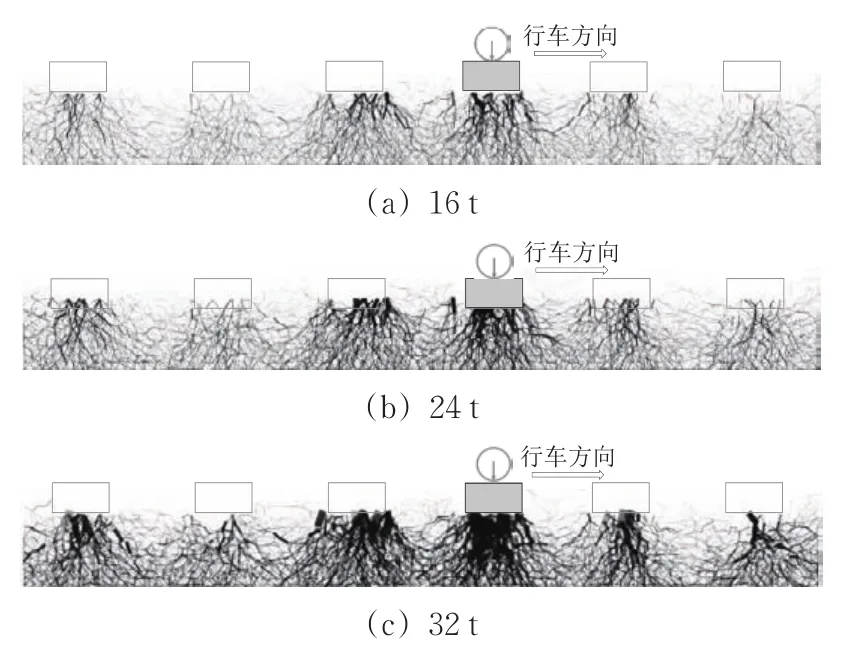
图15 不同轴重下过渡段道床力链图

表2给出了路桥过渡段模型在不同路基刚度分布、不同列车荷载及行车速度下路桥过渡段各路基区的沉降。由表2可以发现：列车轴重对路桥过渡段各路基区的沉降的影响远大于行车速度和路基刚度等因素，这也符合实际工程中重载列车线路过渡段劣化更严重的情况。因此在路桥过渡段尤其是存在重载列车通行时需要采取提高过渡路基区路基刚度等加固措施，以保障列车的行车安全。

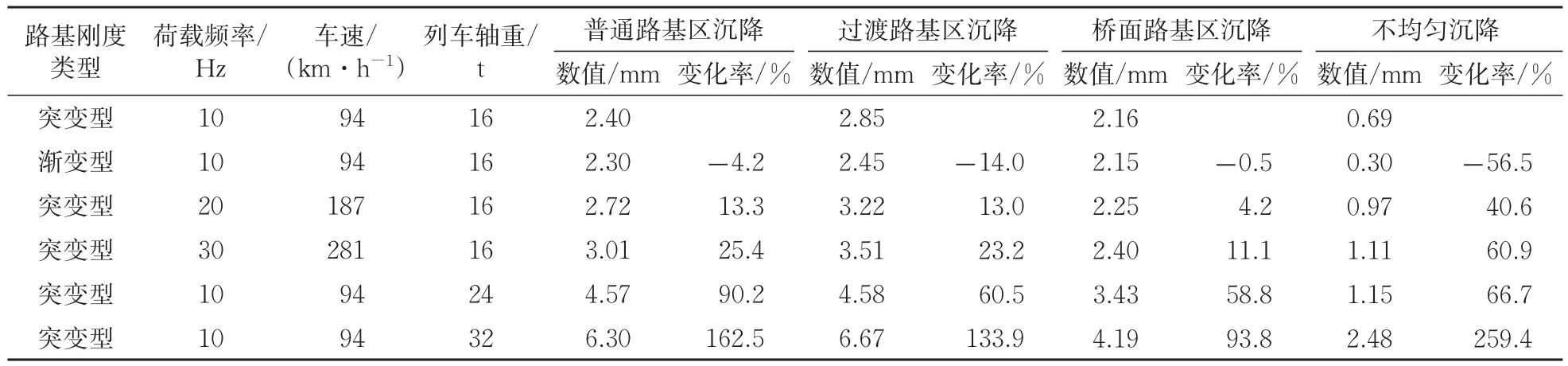
表2 各工况下过渡段各路基区沉降

2.4 软路基段铺设桩基的影响

在实际工程中，路桥过渡段的加固措施主要有2类：第1类为在过渡段较硬一侧（硬路基段）减小轨道竖向刚度，如铺设轨枕垫；第2类则为在较软一侧增大路基基床的竖向刚度。工程中较为常见的方法是在需要加固的路基处铺设混凝土桩或碎石桩等桩基，所铺设的桩用于支撑上部轨道并将荷载转移至路基，如图16所示。由于桩能承受较大荷载，其随时间变化的挠度远小于软土路基填料，因此将桩体打入到不同路基深度可以有效平衡过渡路基区两侧刚度差异，减小过渡段整体不均匀沉降，实现过渡段的平稳过渡[20]。

图16 有砟轨道路基处桩基加固

参考Labrado[21]在过渡段区域采用的短桩加固，将桩体铺设在轨枕的正下方，位于道砟层之下。本文通过增大普通路基区与过渡路基区各轨枕正下方路基弹簧刚度以模拟软路基段桩基，建立图17所示的路桥过渡段桩基加固模型，定性研究路桥过渡段中桩基加固效果。

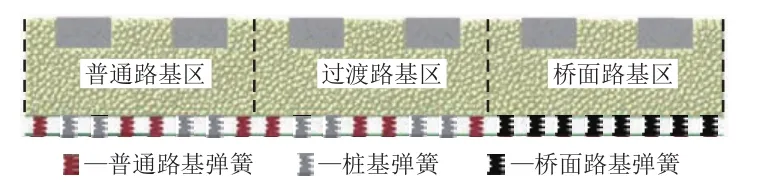
图17 路桥过渡段中桩基加固模拟

图18为采用桩基加固前后，循环加载100次后各路基区的轨枕平均沉降。由图18可见：加固后桩基加固区域上方轨枕沉降均减少，特别是过渡路基区的轨枕沉降减少最明显，其中不均匀沉降由加固前的0.69 mm减小至0.32 mm，减小约53.6%。

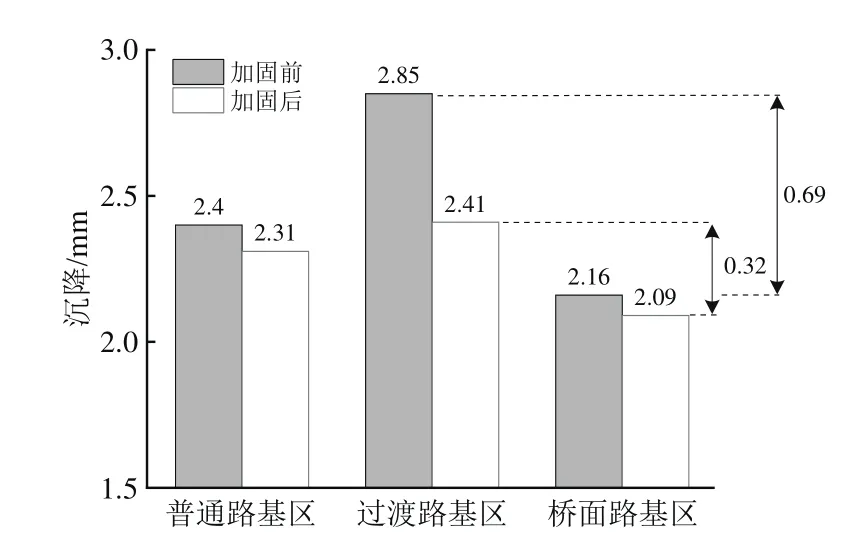
图18 桩基加固前后过渡段各路基区轨枕沉降

图19给出了桩基加固前后道砟速度矢量分布图。由图19可以看出：道砟颗粒的运动主要集中在各轨枕下方区域，荷载主要传递至轨枕下方的桩基。在轨枕下方道砟底部采取桩基加固后，道砟颗粒扰动范围明显减小，同时经过加固后普通路基区道砟颗粒扰动范围与桥面路基区更相近，该模拟结果也验证了在实际路桥过渡段工程中采取桩基加固措施的合理性。

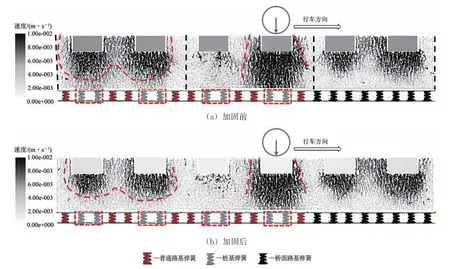
图19 桩基加固与未加固情况下道砟层颗粒运动情况

3 结论

（1）路基刚度突变过渡段模型和路基刚度渐变过渡段模型中最大沉降均位于路桥过渡段中临近桥梁的过渡路基区；路基刚度渐变模型相较于路基刚度突变模型的不均匀沉降减小了56.5%，说明过渡段处路基与桥梁间较大刚度突变是导致不均匀沉降的重要原因，验证了路桥过渡段中对过渡路基区路基采取搭板法加固措施的可行性。

（2）当列车速度由94 km·h−1提升至187和281 km·h−1时，刚度突变过渡段模型中各路基区的沉降均增大，过渡段的不均匀沉降分别增大了40.6%和60.9%；刚度渐变的过渡段模型各路基区沉降以及不均匀沉降随着车速提升增幅相对减小，可见车速提升加快了过渡段劣化，同样验证了搭板法可有效减少路桥过渡段的不均匀沉降。

（3）随着列车轴重的增大，路桥过渡段各路基区的沉降及过渡段的不均匀沉降均显著增大，当列车轴重由16 t提升至24和32 t后，不均匀沉降分别增大了66.7%和259.4%，沉降增加幅度远大于因列车车速、路基刚度变化引起的沉降，因此针对存在重载列车通行的铁路过渡段，更需采取有关加固措施以减少过渡段的不均匀沉降。

（4）在软路基段的轨枕下方采用桩基加固可以减小其与两侧轨枕下路基刚度差，从而减小过渡段的不均匀沉降（约53.6%），验证了桩基加固的合理性，同时具体实际工程中桩径与桩长的选取等还需模型试验进一步的研究。