逆水气变换化工流程热力学优化

赵 明,夏少军,于亚杰

（海军工程大学 动力工程学院，湖北 武汉430033）

0 引言

“碳达峰”、“碳中和”目标的提出，意味着中国能源的转型和变革，可再生能源将在多领域逐渐取代化石能源。其中，在烃类燃料制备领域，通过合成气制备的烃类燃料与传统的以石油加工炼制的烃类燃料相比，具有品种丰富、清洁高效的优点。合成气主要包含CO和H2，可通过生物质在高温和气化剂的作用下气化制取[1]。逆水气变换（RWGS）反应以经太阳能、风能等可再生能源发电后，电解水制得的H2与从大气环境或海水中捕获的CO2为原料制取CO，为非化石能源制合成气提供了一条绿色路线，对于实现碳中和的目标更有意义。

对于化学反应优化，多数学者使用经典热力学的方法对其进行热力学分析，Whitlow[2]和Kaiser[3]分别研究了反应温度对RWGS反应产物的影响和催化剂对RWGS反应转化率的影响。刘昊[4]对甲烷蒸汽重整进行了热力学计算，得到了反应温度、水碳摩尔比等参数对甲烷转化率和出口H2浓度的影响。实际工程反应只是通过经典热力学进行分析还不够准确，它没有将反应中的不可逆性考虑进去。有限时间热力学通过将经典热力学中的“平衡”和传热学、流体力学、化学反应动力学中的“速率”有机结合，求解存在有限温差传热、有限压差流体流动和有限速率化学反应等不可逆性的过程、装置与系统的最优性能与最优构型，所得结果对于指导实际过程和工程装置的最优设计具有重要意义。在RWGS反应器的有限时间热力学研究方面，张磊[5]以反应器的总熵产生率为优化目标，研究了RWGS反应器最优构型，还建立了基于高温氦气加热RWGS反应器的二维拟均相数学模型，以最大径向温差最小和平均转化率最大为优化目标，借助NSGA-II算法对反应器进行了多目标优化[6]。

在实际工程中，需要考虑各个部件对整个流程的影响，仅仅对反应器进行优化可能导致其他部件性能指标的劣化，很难使整体流程的性能目标达到全局最优。与针对单个部件的优化相比，对整个化工流程进行研究更有意义，它可以考虑到各个部件间相互影响及其对整体流程性能的影响，有利于化工流程的整体性能达到最优。与文献[5]，[6]对于单个反应器性能优化不同，本文将利用有限时间热力学理论建立包含混合器、压缩机、换热器和反应器的RWGS化工流程模型，分析反应器进口压力和进口总摩尔流率对流程总熵产率和CO产率的影响，并以总熵产率和CO产率为目标，使用NSGA-II算法对RWGS化工流程进行多目标优化。

1 逆水气变换化工流程模型

工业上进行逆水气反应需要先将反应所需的CO2和H2在环境温度为298.15 K，环境压力为0.101MPa条件下进入混合器混合，然后进入压缩机绝热增压，将混合气体的压力提升到反应所需压力。随后将混合气体通入换热器等压升温，使其温度升至反应入口所需温度。最后混合气体进入RWGS反应器内反应。图1给出了RWGS反应系统的化工流程示意图。

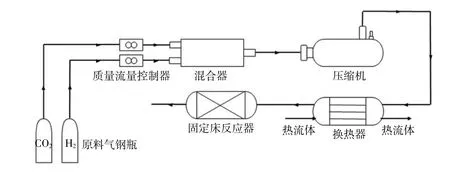
图1 RWGS反应系统的化工流程示意图Fig.1 Schematic diagram of chemical process of RWGS reaction system

由图1可见，系统由混合器、压缩机、换热器、反应器4个部件组成。系统中的气体都假设为理想气体，在每个部件进、出口的质量流率相同，且都满足理想气体状态方程。

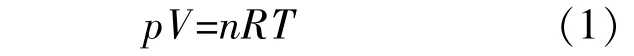
式中：p为气体的压力，Pa；V为体积，m3；n为物质的量，mol；R为理想气体常数，J/（mol·K）；T为温度，K。

气体的等压摩尔热容Cp根据与温度相关的经验关系式计算[7]。

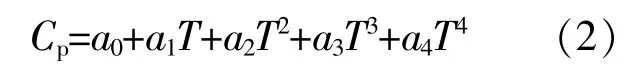
式中：a0，a1，a2，a3，a4为经验参数。

1.1 混合器模型

混合一般是一个绝热等压过程。假设混合过程无反应发生，则混合器输出的气体温度和压力仍是环境温度与环境压力，且气体的组分未发生变化。混合器的熵产率Sg，M为

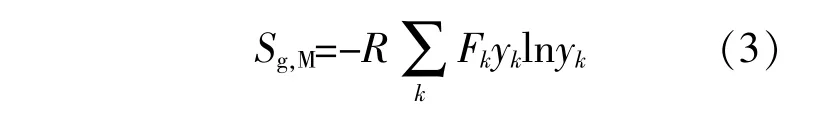
式中：Fk为组分k的摩尔流率，mol/s；yk为组分k的摩尔分数。

1.2 压缩机模型

假设流体的压缩和膨胀是绝热进行的，且具有一定的效率ηc=0.7[8]。压缩过程满足绝热方程。

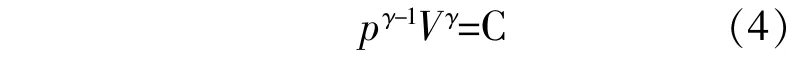
式中：γ=Cp/CV为比热容比；CV为摩尔定容比热容，J/（mol·K）；C为常数。

通过计算可逆情况下输出气体温度来计算实际情况下的输出气体温度。根据联立理想气体状态方程和绝热过程方程，可以得到温度与压力的关系式。

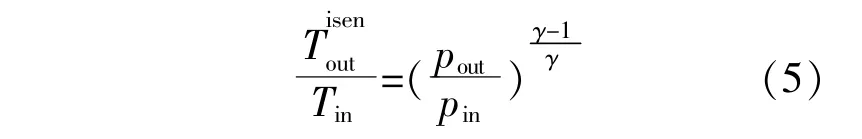
根据压缩效率可以得到

压缩过程熵产率Sg，C为

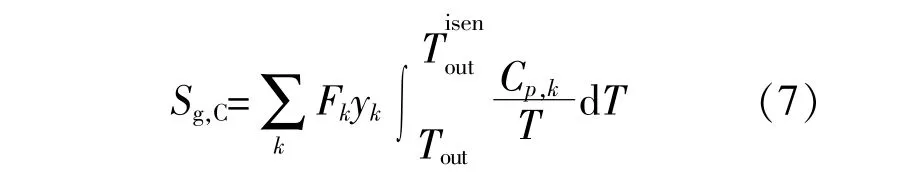
式中：Cp，k为组分k的等压摩尔比热容，J/（mol·K）。

1.3 换热器模型

图1中5号部件为逆流换热器模型，假设热、冷流体在垂直方向已充分混合，忽略流体内部轴向导热和与外部环境传热引起的热漏损失，忽略流体流动压降损失的影响，则换热器传热过程中熵产生主要来源于温差传热。根据以上假定，热、冷流体之间传热服从线性唯象传热规律，则有：

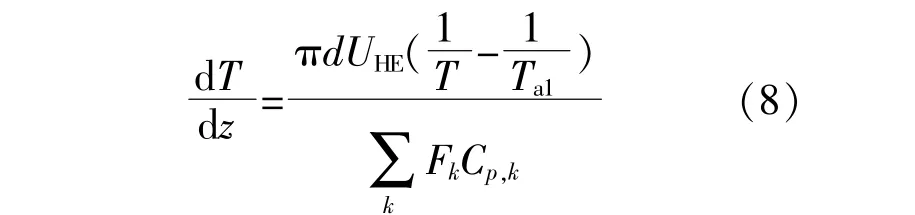
式中：z为换热器的轴向坐标；d为换热器直径，m；UHE为冷热流体间的传热系数，W·K/m2；Ta1为热流体的温度，K。

换热器传热过程中的熵产率Sg，H为

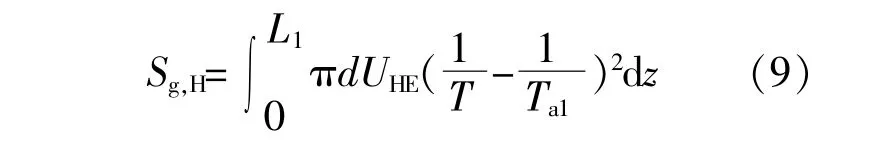
式中：L1为换热器长度，m。

1.4 RWGS反应器模型

考虑到本文反应温度较高，RWGS反应的副反应程度较低，可忽略不计。工业上一般采用多根反应管填充催化剂在反应炉中加热，各个反应管的运行条件相同。因此本文仅对单个反应管进行考虑，如图2所示。

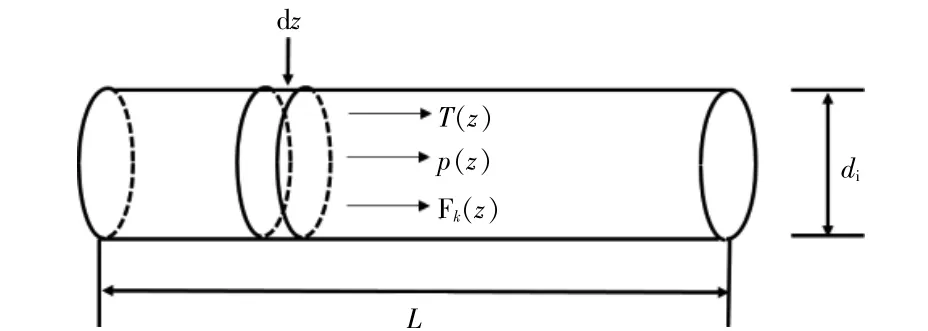
图2 一维活塞流反应器模型Fig.2 Model of the one-dimensional plug-flow reactor

基于一维活塞流假设，对反应器模型做出如下假设[7]：①在稳态下进行操作；②径向混合均匀，即径向上不存在温度、浓度梯度；③管内无返混，即轴向上不存在流体的混合；④管内所有组分均为气态，作为理想气体处理。

该模型满足能量方程[5]：

式中：di为反应器内径，m；UR为反应物与管外热源的传热系数，W/K·m2；Ta2为反应器管外热源温度，K；Ac为反应器的横截面积，m2；ρb为催化床层堆密度，kg/m3；rj为化学反应速率，mol/kg·s；△rHj为反应焓，J/mol。

同时也满足动量和质量守恒方程[7]：

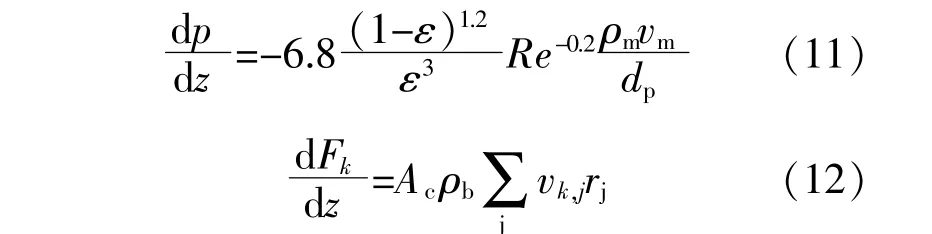
式中：ε为催化床层空隙率；Re为反应混合物气体在固定床反应器中流动过程中的雷诺数；ρm为反应混合物的密度，kg/m3；vm为反应混合物的平均流速，m/s；dp为催化剂颗粒直径，m；vk，j为反应j中组分k的化学计量系数。

RWGS反应速率方程形式可参见文献[5]，[6]。

逆水气变换反应过程中的熵产率Sg，R为

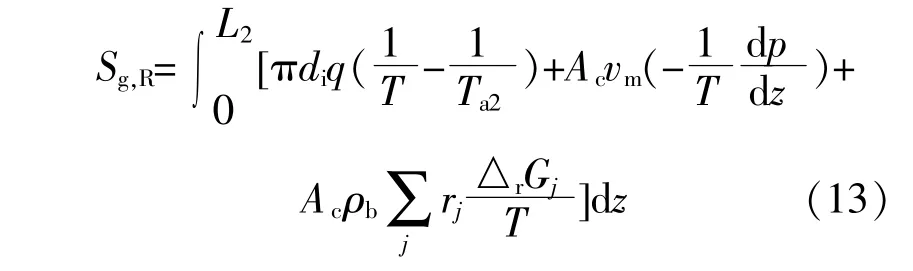
式中：热流密度q=UR（1/T-1/T a2）；△rGj为吉布斯自由焓，J/mol；L2为反应器长度，m。

1.5 优化目标函数

RWGS反应的CO产率△FCO为

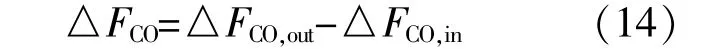
式中:△FCO，out和△FCO，in分别为CO的出、进口摩尔流率，mol/s。

RWGS化工流程的总熵产率∑tot为

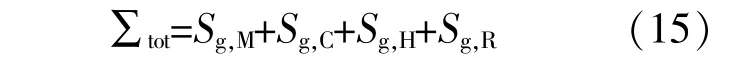
2 优化结果与讨论

2.1 RWGS化工流程分析

通过改变参考化工流程中的反应器进口压力p0和进口摩尔流率FT，in，对参考化工流程的总熵产率∑tot和CO的产率△FCO进行分析，来求得反应器的进口初始条件对整个化工流程的性能指标的影响规律，p0为1～6MPa，FT，in为2.5～8mol/s，表1给出了化工流程各部件工作参数值[5]。

表1 化工流程各部件工作参数值Table 1 Parameter values of each component in the chemical process

图3为反应器进口压力对RWGS化工流程总熵产率和CO产率的影响规律。由图3可以发现，随着进口压力的增加，总熵产率逐渐减小，而CO产率逐渐增大，两者随进口压力的变化曲线在图像中呈上下对称分布，都是变化速率越来越慢，当压力增大到5MPa后，变化规律趋近于一条直线。这主要是因为随着压缩机出口压力增大，压缩过程产生的热量也就越多，使反应器的入口温度增大。进口温度和进口压力的增大都会使反应的速率增大，因此CO产率会随之增大，而增加幅度越来越小是因为RWGS反应在反应器后半段区域已接近化学平衡，进口温度和进口压力对产率的影响逐渐减小。熵产率减小是由于RWGS反应是一个吸热反应，需要较高的反应温度，所以换热器的熵产率在RWGS化工流程中所占比例很大。压力的提高使压缩机出口温度提高即换热器入口温度提高，导致换热器的熵产率降低，RWGS化工流程的总熵产率也就降低。反应器进口压力从1MPa升至6MPa，总熵产率降低了14.9%，CO产率增加了8.2%，因此可以通过提高反应器进口压力来使总熵产率降低的同时增加CO产率。

图3 进口压力对总熵产率和CO产率的影响Fig.3 The influence of inlet pressure on the total entropy production rate and CO production rate

图4为进口总摩尔流率对总熵产率和CO产率的影响规律。

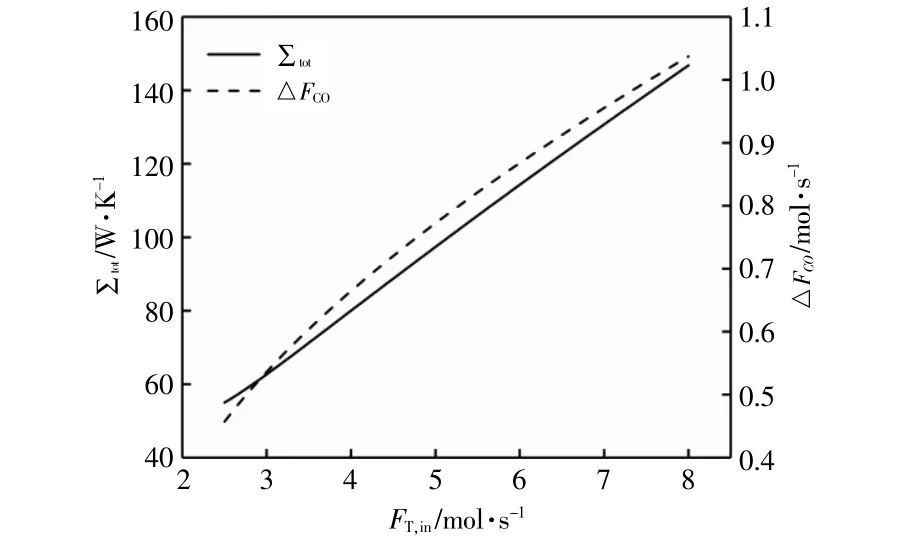
图4 进口总摩尔流率对总熵产率和CO产率的影响Fig.4 The influence of the total inletmolar flow rate on the total entropy production rate and CO production rate

由图4可以看出，总熵产率和CO产率都随着进口总摩尔流率的增大而增大，所以不存在一个最优的进口总摩尔流率同时满足总熵产率最小和CO产率最大。进口总摩尔流率的增大意味着反应物物质的量的增加，所以各部件的熵产率都会增加，反应速率也会加快。当进口总摩尔流率从2.5mol/s增加到8mol/s时，总熵产率约增加为原来的2.7倍，CO产率约增加为原来的2.3倍，即进口总摩尔流率对总熵产率和CO产率的影响程度相似，对CO的影响较小。

2.2 基于NSGA-II的多目标优化

根据前文可知，当以反应器进口压力和进口总摩尔流率两个参数为优化变量对RWGS化工流程进行优化时，不能同时满足总熵产最小和CO产率最大。因此，在两个目标之间进行协调和权衡，使各个目标尽可能达到最优值是迫切须要解决的。本文采用NSGA-II算法，以反应器的进口压力和进口摩尔流率为优化变量，对RWGS化工流程总熵产率和CO产率进行多目标优化。

设置种群数目为100，优化目标为2，优化变量为2，遗传代数为100，利用PlatEMO工具箱算得RWGS化工流程基于总熵产率最小和CO产率最大为目标的Pareto最优前沿，结果如图5所示。

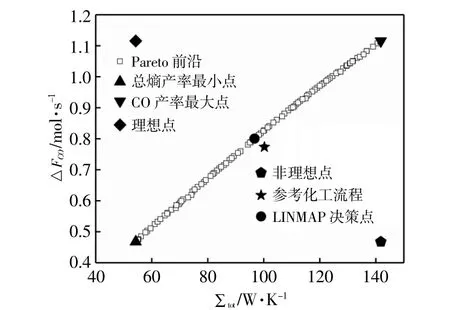
图5 化工流程的Pareto最优前沿Fig.5 Pareto frontof chemical process

由图5可知，总熵产率最小点和CO产率最大点所对应的CO产率和总熵产率在Pareto前沿上都是最不理想的，这再次验证了在RWGS化工流程中最小总熵产率和最大CO产率不能同时满足，只能求得两个目标在不同重要程度下的最优解。总熵产率最小点和CO产率最大点都是在不考虑其中一个目标的情况下对另一个目标进行单目标优化的结果。本文利用LINMAP决策方法，设置总熵产率和CO产率的权重都为0.5，得到了LINMAP决策点。与参考化工流程点相比，LINMAP决策点的总熵产率和CO产率均更理想。

表2给出了参考化工流程与优化后化工流程的优化变量与性能目标参数值。由表2可知：与参考化工流程相比，只对总熵产率进行优化使总熵产率减小了45.8%，CO产率减小了39.5%；只对CO产率进行优化使CO产率增加了44.2%，但会使总熵产率也增加41.5%。利用LINMAP决策选出的Pareto前沿上的多目标优化点，总熵产率减小了3.5%的同时CO产率增加了3.5%。在参考化工流程点左上方的所有Pareto前沿点都是使熵产率减小的同时CO产率增大，对参考化工流程都具有多目标优化的作用。

表2 参考化工流程与优化后化工流程的优化变量与性能目标参数值Table 2 Parameter values of the optimization variables and performance objectives for the reference and optimized chemical processes

图6，图7分别为反应器进口压力和进口总摩尔流率在Pareto前沿中的分布。

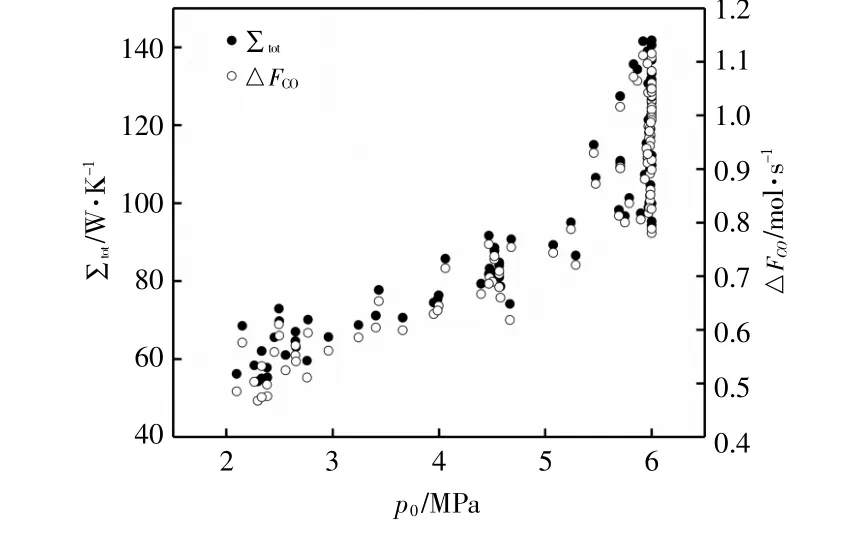
图6 进口压力在取值范围内的分布Fig.6 Distribution of inlet pressure in their variation range

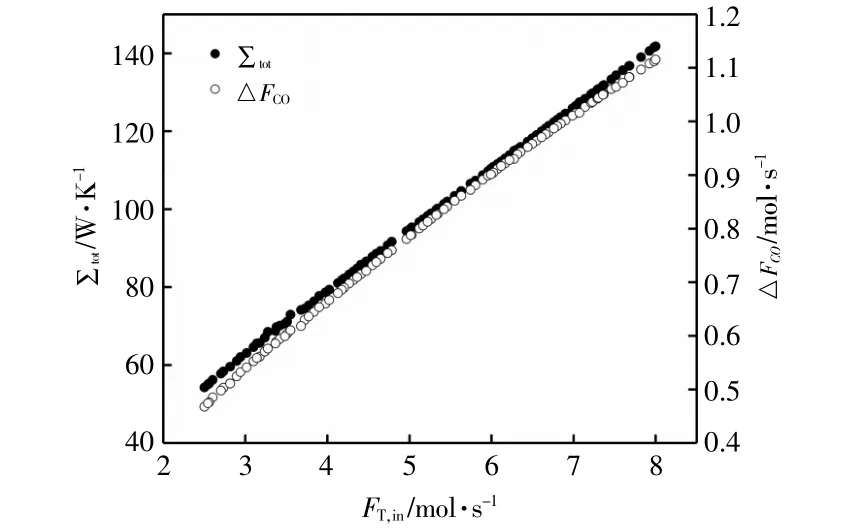
图7 进口总摩尔流率在取值范围内的分布Fig.7 Distribution of inlet totalmolar flow rate in their variation range

由图6，图7可见，在Pareto前沿中，进口压力的优化区间主要集中在取值范围的上限附近，进口总摩尔流率则在其取值范围区间分布均匀。这说明提高进口压力是对RWGS化工流程多目标优化的主要手段，而调整总摩尔流率则是为了平衡总熵产率和CO产率，避免追求一个目标的同时过于牺牲另一个目标。

3 结论

本文基于有限时间热力学理论分析了RWGS化工流程的反应器进口压力和进口摩尔流率对其总熵产率和CO产率的影响，并以反应器的进口压力和进口总摩尔流率为优化变量，利用NASAII算法对其进行多目标优化，得出以下结论。

①随着进口压力的增加，总熵产率逐渐减小，而CO产率逐渐增大，且变化速率都随压强增大逐渐减小。随着进口总摩尔流率的增大，总熵产率和CO产率都增大。

②优化得到的Pareto前沿包含了对RWGS化工流程在参数范围内对两个目标不同权重下的多目标优化结果，权重为1和0时，结果为在参数范围内的单目标优化。利用LINMAP决策方法在Pareto最优前沿上取得的决策点与参考化工流程相比，总熵产率减小了3.5%的同时CO产率增加了3.5%。

③本文计算结果可为RWGS化工流程的设计提供了理论指导。