考虑分布式可再生能源的配电网电力调度优化模型研究
2022-06-09马临超齐山成
马临超,齐山成,刘 毅,杨 捷
(河南工学院,河南 新乡 453003)
0 引言
近年来随着大规模可再生分布式电源(Distributed Generation,DG)的集成,为配电网的电力调度工作带来了新的挑战[1],[2]。配电网的电力调度问题已成为研究人员关注的焦点[3],[4]。
传统电力系统模型中有功和无功(Active Power and Reactive Power,P-Q)是去耦的,利用功率因数解耦特性,电力传输网络中的功率因数控制可以分为不同的阶段。一般认为有功功率分配是由日前的电能消耗和实时的电能损耗阶段确定的,电压/无功功率需要实时调节,以最大限度地减少电网功率损耗,改善电压特性,并限制电网过电压[5]~[7]。然而在配电网中,输电线的电阻与其电抗相当,这意味着有功功率对电压的影响很大,并且功率因数无法去耦。实际运行经验表明,DG集成的高渗透水平将导致反向功率流和过压问题。因此需要同时考虑有功功率和无功功率,以确保系统的电压安全。与无功功率不同,控制有功功率会增加成本,如发电机的调节成本和风电出力的削减成本[8],[9]。此时,传统实时调度模型中做出的有功发电决策可能会增加顺序校正控制阶段的调节成本,或者导致缺乏可行的控制策略来满足所有安全要求。因此,应将有功功率调度和校正控制集成在一个通用模型中,以最大限度地降低总体成本并增强系统安全性。同时分布式发电整合具有较大的不确定性,由于可再生能源(如光伏和风力发电)的间歇性和波动性,分布式发电的有功功率输出会因天气条件的变化而波动,难以准确预测[10]。因此分布式发电输出中的不确定性问题,必须在实时电力调度模型中得以解决,以确保所有可能情况下电力系统的安全性,并提供统计上最佳的有功功率分配决策。
本文采用多阶段非确定性优化模型代替传统的单阶段确定性模型,提出了一种分布式鲁棒两阶段优化(Distributed Robust Two-stage Optimization,DRO)模型,用于解决配电网中的实时电力调度问题。通过在一个通用模型中集成有功功率调度和校正控制,使得有功功率和无功功率控制在不同的时间尺度上得到很好的协调。最后,通过IEEE 39和IEEE 123总线系统对提出的模型进行了数值实验分析,验证了模型的有效性。研究结果可为分布式可再生能源的实时电力调度提供参考。
1 数学模型
1.1 优化目标函数
在本文的DRO模型中,主要考虑了两种类型的设备:分布式燃料发电机(以下称为发电机)和可再生能源驱动的分布式发电系统(以下称为分布式发电系统)。在经济调度(Economic Dispatch,ED)阶段,主要针对发电机组制定输出功率计划;在校正控制阶段,调节分布式发电系统和发电机的有功功率和无功功率,以确保最小的控制成本和系统安全性。因此,总成本由发电成本和校正控制成本组成。
此外,为了模拟配电网和输电网络之间的电力交换成本,将输电网络简化为二级电力市场,大致等同于前向市场和实时市场。在经济调度阶段,从一级市场购买近似有功功率需求,在校正控制阶段,从二级市场购买有功功率需求与之前近似值之间的差值,其中一级和二级市场的电力价格不同。
①发电成本
发电成本主要由所有发电机的单个成本之和G(x)以及从一级电力市场购买的成本Gi(PGi)两个部分组成。

式中:x为第一阶段决策变量的向量,包含pflPfl(单个发电机成本)和Gi(PGi)两项;ai,bi,ci为发电机的软成本函数;NG为所需考虑的成本。
②校正控制成本

可再生能源发电量的低估和高估惩罚基于实际可再生能源发电量与其预测值之间的偏差,通过设置适当的惩罚系数,基于偏差的惩罚即可促进可再生能源的利用。
1.2 模型约束
①发电机和分布式发电系统的输出限制
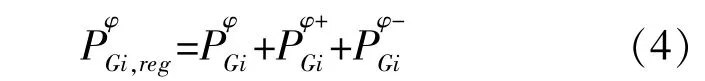

式(4)和式(5)分别描述了校正控制阶段操作动作燃料发电机和可再生能源发电机组的有功功率输出的影响;式(6)~(10)分别为燃料发电机和可再生能源发电机组的功率输出约束。
②操作约束

在式(11),(12)中,有功功率的产生受到燃料发电机调节能力的限制。为了简化问题,假设调节能力是固定的,并且与在经济调度阶段的决策无关,以相同的方式求解调节能力与的模型。
③潮流约束
本文使用分支潮流模型描述具有径向结构的配电网潮流,在三相配电网中精确的支路潮流方程为

式中:s,v,i为3×1的复数向量,分别代表功率、电压和电流;下标i,k分别为节点编号和有功分量;下标m为无功分量;上标d为正交项。
精确的三相功率流模型包含一个双向耦合和一个正交网络。本文使用了近似三相分支的流动模型,用泰勒级数估计非线性项,并保证模型具有较高精度。


式中:pik,pkm,qik,qkm分别为支路的有功和无功功率流;为母线电压的平方;分别为母线的有功和无功功率需求,模型中假设功率需求是确定的;Bik,Gik,Hik,Kik,Rik,Xik为三相矩阵;矢量为预先计算的参数。
式(16),(17)相当于母线k的功率平衡等式;式(18)描述了支路ik的电压降。
④支路热约束

式中:i,j为节点编号。
上标φ使用二次约束线性化方法,引入多线性约束代替式(19),可得:

1.3 可再生能源出力不确定性模型
式(3)中给出了校正控制成本,但实际成本是通过如下优化问题求解目标函数的最小值:

由于式(26)的约束中存在x和h(不确定变量的向量,包括PDGi,max),可以将校正控制成本表示为x和h的函数。

利用给定的x和h值,通过求解式(27)即可算出相应的校正控制成本。如果h的概率分布给定为显式P,则D(x,h)的期望值为EP[D(x,h)]。
本文提出的DRO模型中,假设不确定变量h的概率分布被约束在一个模糊集合Ω中,而不以明确的形式给出。为了评估由实时调度决策产生的校正控制成本,选择分布式发电输出的最坏情况的概率分布中的期望作为第二阶段目标,这一思想类似于鲁棒两阶段优化(Robust Two-stage Optimization,RO)模型。
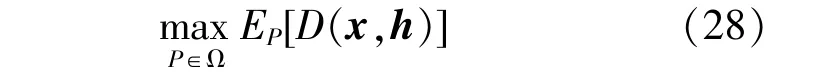
本文采用基于矩的估计描述概率分布模糊度,通过假设集合中所有可能的概率分布具有相同的均值向量μ和协方差矩阵∑来构造模糊集,模糊集Ω(μ,∑,S)数据基于历史DGs输出曲线依据经验计算。

其中S定义了限制DG输出上限范围的支持集h,本文采用椭球形式的支持集:

Ω(μ,∑,S)比RO模型中的不确定性集更能利用不确定变量的分布特征,与阶段优化(Stage Optimization,SO)模型不同的是,歧义集的构造不需要假设DG输出的概率分布的确切形式。
实时电力调度的DRO模型的完整形式可写为
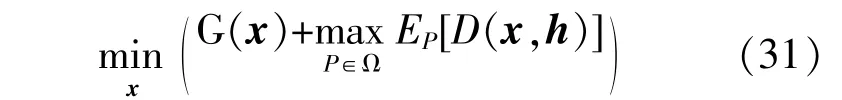
为避免混淆,校正控制成本实际上是通过求解校正控制过程中已知的、与之相关的优化问题而获得的,D(x,h)的引入只是为了强调最优控制成本,可以由给定的x,h值确定。
1.4 模型求解方法
本文采用约束延迟算法求解优化模型。与其他优化模型的求解过程不同,约束延迟算法通过逐步加入约束的方法,缩小最优解的范围,经迭代计算得到最终的结果,保证了模型的收敛性,有效地克服了约束方程组较多时带来的高度非线性问题和算法不收敛问题。
求解步骤:①模型初始化;②求解主问题;③求解可再生能源处理不确定性问题;④逐个添加约束条件,迭代更新优化解。模型求解流程如图1所示。

图1 优化模型求解流程示意图Fig.1 Solution process diagram of optimizationmodel
2 实验分析与模型验证
本文采用IEEE 39优化总线和IEEE 123优化总线测试系统,对提出的配电网实时调度模型性能进行实验分析,验证模型的有效性。实验时,将本文提出的方法(DRO法)与一阶RO法(OSRO法)和两阶RO法(TSRO法)进行对比。
OSRO模型忽略了第二阶段的校正控制操作和电压约束,只考虑发电机的最优有功功率输出分配和分布式发电输出的不确定集,以保证在任何情况下都不违反支路功率界限的约束。TSRO模型与DRO模型几乎相同,但它将最坏情况下的校正控制成本视为第二阶段的目标函数,并且没有考虑分布式发电输出的概率分布信息。
2.1 IEEE 39总线系统实验
本文采用的测试系统是一个由39条总线组成的辐射状配电网。所有发电机和分布式发电系统分三相连接到电网,假设每相的有功功率输出相等。IEEE 39总线测试系统模型见图2。实验时采用DRO,OSRO,TSRO 3种方法同步进行计算,通过比较和讨论得到本文模型的效果。
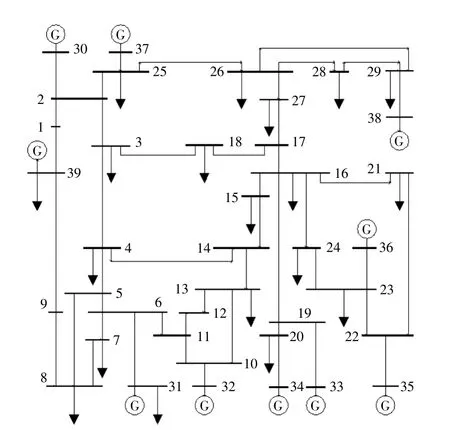
图2 IEEE 39总线系统示意图Fig.2 IEEE 39 bus system diagram
(1)DRO法和OSRO法的比较
假设不确定向量h的一阶矩μ和支持集的半径是固定的,使用交替协方差矩阵比较DRO和OSRO模型的性能。为了简化比较,假设3个DGs的输出上限是独立的,并且具有相同的方差σ2。
使用蒙特卡罗方法评估由调度决策产生的校正控制成本,选择多变量正态分布作为测试数据的特定概率分布,该分布具有均值向量μJ和协方差矩阵∑。随机生成N个不确定向量h的样本,并求解式(31)以确定每个生成场景的校正控制成本。然后计算所有场景的平均校正控制成本,并将其添加到第一阶段成本中以确定总成本。
图3、图4所示为N=5 000时采用不同σ2和支持集的计算结果。由图可见:两种方法的总成本随着不确定性变量的增加而增加,这是因为在波动性较大的情况下,系统需要采取更多的操作措施来保证DGs输出的安全性;DRO法的总成本始终低于OSRO法,这是因为DRO模型以稍高的发电成本为代价做出的调度决策产生了最佳的校正控制成本。本文以σ2=0.05的模拟数据为例,详细地研究了校正控制成本的差异,结果表明,DRO法的环保决策比OSRO法保守,导致第一阶段发电成本更高,但是DRO法的调度改善了电压分布。模拟实验显示,在经济调度决策为100%的情况下,OSRO法会导致过电压问题,而DRO法导致过电压的比例仅为26.5%。

图3不同方差的DRO法和OSRO法的总成本Fig.3 Costof DRO and OSROmethodswith different variances

图4不同支持集的DRO法和TSRO法的总成本Fig.4 Cost of DRO and TSROmethodswith different support sets and variances
本文比较了不同模型的校正控制措施,结果显示,发电机和分布式发电系统的有功功率输出均下调,以缓解OSRO模型中的过电压问题,这将导致校正控制成本的增加和可再生分布式发电输出削减程度的提升。相比之下,DRO模型的调度决策减轻了过电压问题,无功功率资源足以保证系统在分布式发电输出波动情况下的安全性。因此,既不需要对发电机进行有功功率调节,也不需要削减分布式发电的输出,从而降低了控制成本,提高了可再生能源的利用率。
总的来说,通过在DRO模型中建模电压约束、耦合有功功率和无功功率,DRO实现了比OSRO更低的成本和更好的可再生能源利用,部分解决了由DG集成引起的过电压问题,并减轻了校正控制阶段的负担和成本。
(2)DRO法与TSRO法的比较
DRO法与TSRO法的主要区别在于概率分布信息的利用方法,DRO法同时考虑了暂态信息和支持集,而TSRO法仅将后者视为不确定性特征。本文通过同时改变协方差矩阵和支持集的半径来比较DRO模型和TSRO模型的总成本。由于多变量正态分布用于模拟具有特定一阶矩和二阶矩的具体分布,支持集应该覆盖每个变量的三西格玛区间,因此采用不确定集的半径r=3σ2进行简化比较。
表1为IEEE 39总线系统采用DRO法和TSRO法的计算结果。由表可知,随着支持集半径的增加,DRO和TSRO的总成本增加,当支持集半径较小时,两种方法的性能相似,支持集半径较大时,DRO法的优势变得更加明显。上述结果反映了DRO法和TSRO法之间的差异。可见TSRO的调度决策更保守,使得在最坏的情况下调度成本最小,但在其他情况下是次优的。实际上极端的最坏情况很少发生,TSRO的调度效果并不是最佳的。相比之下,DRO利用已知的概率分布信息来调整目标函数中不同情景的权重,降低了风险值的保守性。因此在极端情况下,DRO以稍高的成本为代价实现了统计上的最优成本,使得DRO法更适用于工程实际。

表1 IEEE 39总线系统采用DRO和TSRO计算结果Table 1 DRO and TSRO calculation results for IEEE 39 bus system
表2为采用不同方法下新能源不稳定出力时的总线过电压计算结果。可见,采用DRO法能够较好地避免总线过电压问题。

表2 IEEE 39总线系统在新能源不稳定出力情况下,总线出现过电压的计算结果Table 2 Calculation results of bus overvoltage in IEEE 39 bus system under unstable outputof new energy
2.2 IEEE 123节点总线系统实验
本文利用所提出的DRO模型,在IEEE 123总线系统中进行了测试,以评估其在大规模和高度不平衡的三相配电系统中的性能和可扩展性,IEEE 123总线测试系统如图5所示。

图5 IEEE 123节点总线系统示意图Fig.5 IEEE 123 bus system diagram
实验计算时采用DRO,OSRO,TSRO 3种方法同步进行,通过比较得到本文模型的效果。
(1)DRO法和OSRO法的比较
假设支持集的半径是常数,在相同支持集半径下,比较两种方法总成本的差异。图6为N=5 000时的蒙特卡罗模拟结果,与IEEE 39节点系统的结果类似,DRO法在总成本方面优于OSRO法,因为其纠正控制成本较低。

图6不同方差下DRO和OSRO方法的成本Fig.6 Costof DRO and OSROmethods under different variances
(2)DRO法与TSRO法的比较
假设r=3σ2,通过同时改变支持集的半径和发电机组输出的方差,比较DRO和TSRO的性能。具有不同支持集的两种方法的成本如图7所示。可见在所有情况下,DRO模型在成本预期方面都优于TSRO模型,TSRO模型在极端情况下的成本略低,通过利用分布式发电输出中的概率信息验证了DRO法的统计最优性。
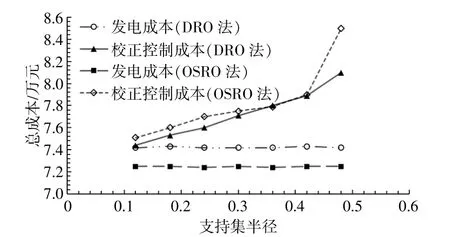
图7不同支持集的DRO法和TSRO法的成本Fig.7 Costof DRO and TSROmethodswith different support sets
表3为IEEE 123总线系统采用DRO法和TSRO法的计算结果。由表可知:采用DRO法得到的预期成本相比TSRO法要低,并且减少的成本百分比随支持集半径的增加而增加;支持集半径由0.12增大至0.42,采用DRO法可节约的预期成本相比TRSO法降低了23.23%。可见,采用DRO法可有效减少预期成本。
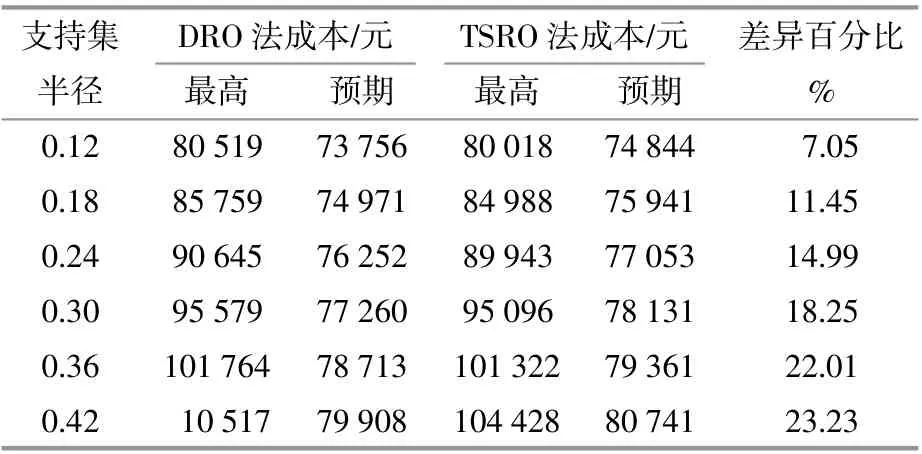
表3 IEEE 123总线系统采用DRO和TSRO的计算结果Table 3 DRO and TSRO calculation results for IEEE 123 bus system
表4为采用不同方法下新能源不稳定出力时的总线过电压计算结果。可见,采用本文的DRO法,能够较好地减少总线过电压问题。

表4 IEEE 123总线系统在新能源不稳定出力情况下,总线出现过电压的计算结果Table 4 Calculation results of bus overvoltage in IEEE 123 bus system under unstable output of new energy
3 结论
①实验结果表明,DRO调度决策方法与TSRO法相比,降低了校正控制成本和总成本。案例计算结果表明:对于IEEE 39总线系统,DRO法可节省13.84%的成本;对于IEEE 123总线系统,DRO法可节省23.23%的成本,有效降低了调度成本。
②本文提出的DRO法有效地缓解了过电压状态,与TSRO法和OSRO法相比,在IEEE 39总线情况下,DRO法避免了过电压的出现;在IEEE 123总线情况下,DRO法明显降低了出现过电压的母线数量。表明本文提出的DRO法更适合工程实际。
③本文采用逐步添加约束求解优化模型的方法,降低了模型的非线性程度,提升了算法的收敛性;同时通过迭代计算的方法保证了计算结果的准确性。该方法对于求解大型优化问题具有一定的参考价值。
