“转化思想”在小学数学教学中的运用及培养
2022-06-07武汉城市职业学院初等教育学院黎静芳
■ 武汉城市职业学院初等教育学院 黎静芳
数学课程标准(2011版)在总体目标中第一次提出了“四基”的理念和目标,特别重视数学思想及其具体实施。这对小学数学教师而言挑战很大,他们除了数学思想方法的专业知识不足外,还有课堂教学中应该具备的相关理念、策略也不足;基于以上原因,我们有必要研究数学思想方法的相关问题。
数学思想方法有不同的分类,王永春教授把它们分成四类;本文探讨与推理有关的“转化思想”及其在教学中的运用和培养。
一、对转化思想的理解
“转化思想,就是指把数学中不能解决或需要解决的问题,在头脑中经过重组和变化,与原有的知识经验建立联系,化归为之前已经解决过的问题,最终使新问题获得解决的一种手段和方法”这是张奠宙教授对转化思想的定义。
应用转化思想的本质就是将一个新问题转化为旧问题、将一个繁杂的事物转化为简明的事物,从而揭示数学本质,最终达到优化解题策略的过程。
二、转化思想在教材中的体现
转化思想在小学数学知识的四大领域及“数学广角”中都有体现,分布在每册教材里并不成体系,我们有必要将相关内容进行梳理,帮助教师在教学时顺利把转化思想的应用渗透给学生。
1.在学习抽象的“数及运算的意义”时运用转化
表1对人教版教材中“数及运算的意义”教学内容进行了梳理,我们发现将比较抽象的“数的意义”及“运算的意义”运用实物的操作或者直观图展示后,可以帮助小学生更好地理解这些概念,这种化抽象为具体的转化策略需要教师不断渗透,学生才能在解决问题的过程中慢慢领会这种思想方法。

表1 人教版教材学习“数及运算的意义”时转化思想应用
2.在学习四则运算法则时,将新运算转化成已学过的运算
表2对人教版教材中四则运算法则的教学内容进行整理,发现利用转化就可以把新的运算法则转化为已经学习过的相应的法则来计算,这样不仅优化了解决问题的方法,也让学生在学习新知过程中体会转化思想方法的应用。
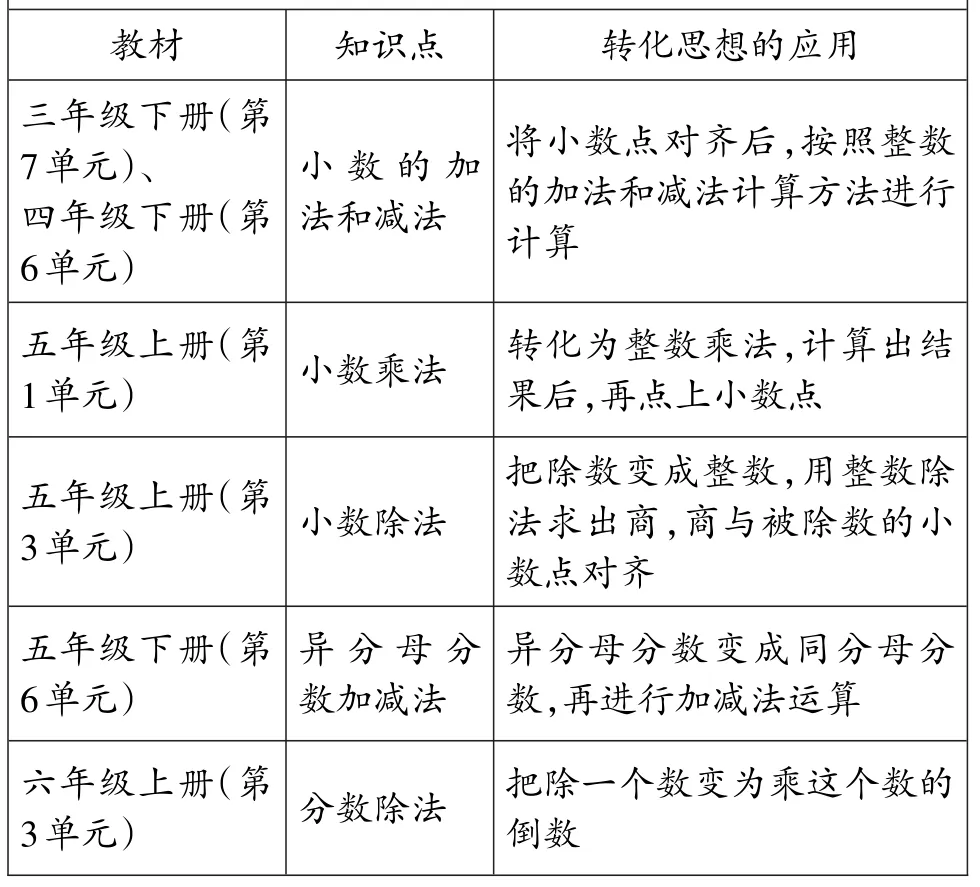
表2 人教版教材“四则运算的意义和运算法则”转化思想应用
3.在各种计算中利用运算定律和性质进行转化达到化繁为简
例1 三年级上册,第2单元万以内的加减法
①两位数加减两位数的口算转化:63-48=63-40-8=23-8=15;
②几百几十加减几百几十的笔算转化:
求550-380转化为55-38=55-30-8=25-8=17,所以550-380=170;
例2 四年级下册,第23页第9题,利用恒等变形把等式化简:
1+2+3+…+98+99+100=(1+99)+(2+98)+…(49+51)+100+50=100×50+50=5050
例3 四年级下册,第29页例8,利用运算定律进行简算:
12×25=(3×4)×25=3×(4×25)=3×100=300
或者12×25=(10+2)×25=10×25+2×25=250+50=300
从这三个例子可以看出,我们将新的运算转化为已经学过的定律和性质来计算,可以达到简算和速算以及灵活运用的目的。
4.在多边形内角和、多边形的面积与体积公式学习中应用转化
以人教版为例,在图形与几何方面转化思想的应用如下:
从表3我们可以看出,转化思想在各册教材的“图形与几何”这一部分基本都有体现。因此需要教师认真领会教材,在教学中有目的、有组织地将所运用到的转化思想揭示给学生,进行合理渗透。

表3 图形与几何领域转化思想的应用
三、转化思想在课堂中的培养路径
转化思想的运用无时不有、无处不在,对培养学生的探究能力十分重要。教师要注重数学思想转化的方式,以便呈现清晰的数量关系,降低学习的难度,从而提高课堂教学效果。下面探讨在教学中培养转化思想的几点思路及应用原则。
1.在数学教学中使学生逐步养成转化的习惯
转化思想的形成是一个循序渐进的过程,让学生经历应有的历练是形成的前提,教师在教学过程中提供时间与空间则是数学思想形成的保证。
(1)做好教师引领示范。教师的引领一方面是授课时应用转化思想方法的示范,另一方面是教给学生进行转化的技能,在课堂上为学生创造运用转化思想的时间和空间。教师示范所展示的结论要令人信服,在解决问题的全过程中如何体现转化思想则更为重要,也就是让学生弄明白解题的思路是如何想到的、思想方法是如何运用的,通过比较反思,转化思想方法的优势就能体现出来了。
(2)用好集体互动功能。学生数学思想的形成离不开班集体的互动,因为每个人的成长都会受到集体影响,与同学交流中获得肯定是学生进步的动力。个体将他人的观点与自己的方法进行比较,在相互交流和争论中,让多种思维方式汇集在一起,这样转化思想解决问题的优势就会显示出来,从而让学生开阔思路、体验成功。这个过程让每个学生的思维更清晰,也使班集体解题的方式更丰富,全班一起受益。
(3)发挥评价的导向作用。转化思想的应用在数学活动的结果中往往体现不出来,而是呈现在思维方式与过程中,呈现在解决问题手段的有效性、策略的合理性上,因此在评价方式和内容上,教师鼓励学生展示转化的思维过程,通过对策略和方法的优劣做比较,来强化和刺激学生的行为,就能很好地促进小学生转化思想的形成。
2.转化思想应用的原则
转化思想的本质是在已学过的相关知识的基础上,把繁杂问题化为简洁的问题、把抽象事物化为具体事物、把非常规对象化为常规对象,从而达到问题解决的目的。为此,在运用转化思想时要遵循的原则有以下几个:
(1)数学化原则,就是把一般问题向数学问题转化,通过建立数学模型,应用已有的知识来解决问题的方法。数学具有广泛的应用性,利用所学知识解决生活中的问题是学习数学的目的之一。
(2)熟悉化原则,就是把陌生的事物转化为熟知的事物。数学的学习过程就是一个把新知内化为旧知、使新问题不断解决的过程。这个过程不仅是一个探索的过程,也是一个创新的过程,培养探索能力和创新精神也是课程标准所提倡的。
(3)简单化原则,即把数量关系繁杂的问题转化为数量关系简单的问题。对学习者而言,复杂的问题或许能够解决,但所经历的过程往往会很麻烦,而经过相关的转化后,可以寻找到一些技巧和捷径,使解决问题的过程得到优化。
(4)直观化原则,即把抽象的问题转化为直观具体的问题。数学的特点之一是抽象性,直接解答抽象的问题难度较大,借助直观手段把抽象问题转化为比较具体的问题后,解决起来就比较容易了。
下面是遵循以上原则,我们利用转化思想解决几类典型问题的案例。
四、转化思想的拓展应用
1.分率转化
对于某些比较复杂的分数应用题,当题目里出现多个单位“1”,即有多个不同的分率时,我们应当通过转化把它们化成单位“1”相同的分率,再根据数量关系进行解答。
例1 把一根木材裁成三节,使第一节的长度等于余下两节的和;第二节又等当于第一节与第三节之和的一半;已知第三节长米,求这根木材长多少米?

分析与解:此题如果把木材分成三个小节分别去计算,那是相当困难的,但把全长作为单位“1”,把几个分率进行转化就非常简捷了。题目说“第一节的长度等于余下两节的和”,从全长考虑,第一节即为全长的,再从“第二节又等于第一节与第三节之和的一半”,如果把第二节看成1份,另外2节之和就是2份,从全长考虑,第二节就占全长的。第三节所对应的分率为:
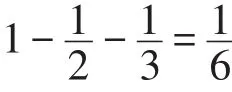
答:这根木材全长4米。
2.题型的转化
在各种转化中,难度最大、应用范围最广的应是题型的转化了。
例2 已知四个自然数A、B、C、D,它们的大小依次增加。B、C、D三个数和的正好与甲相等,A、B之和与C、D之和的是相等的。想使A、B、C、D的总和最小,而C尽可能大,D的取值是多少?
分析与解:这道题中有两个分率,第一个分率是以B、C、D三个数的和为单位“1”,第二个分率是以丙、丁的和为单位“1”,如果用分数问题的一般解法是很困难的,我们运用转化就可以使问题变得简单。
题目的条件“想使A、B、C、D的总和最小”,7和11的最小公倍数77即为这四个数的最小总和。那么C、D两个数的和为:

因为C<D(A、B、C、D数值是依次增加的),又要“让C尽可能大”,所以,D只能为25。
答:D应当等于25。
3.图形转化
例3 已知三角形ABC的面积是40平方厘米,它的面积是平行四边形CDEF面积的倍。求三角形EFB的面积?

分析与解:阴影三角形BEF是一个一般三角形,题目中只有一个数值40,根据这个值想得到所求三角形EFB的底和高都是不可能的。那么我们能不能找到一个三角形与所求三角形面积相等呢?如右上图,连接E、C后发现:新三角形ECF和三角形BEF的底EF是相同的,而CDEF是平行四边形,则它们的高也相等。那么,这两个三角形面积相等,题目就转化为求三角形EFC的面积了。
在平行四边形CDEF中,三角形EFC的面积是平行四边形CDEF面积的一半,所以EFB面积也就等于平行四边形CDEF面积的一半。
通过“转化”,列式可求出:
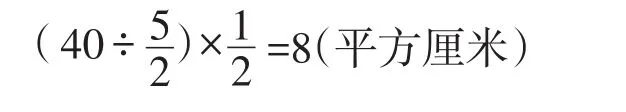
答:三角形EFB的面积为8平方厘米。
以上三个例题说明,我们通过恰当的转化,就能把未知变成已知,把繁杂的问题转化成已有的经验,从而使问题顺利得以解决。
五、结语
转化思想是数学解题中重要的、基本的思想方法之一,许多困难问题通过转化变得容易。教师在教学中转化思想的渗透不仅拓宽了学生的思路,还提高了学生分析和解决问题的能力;在培养学生多角度考虑问题的过程中,不仅让他们养成了良好的思维习惯,而且学生的思维品质得到了优化,运用数学思想方法的能力不断提升。
