基于ST DBSCAN 的航迹聚类实现

朱瑜亮

(中国电科集团第十研究所，四川 成都 610036)

0 引言

航迹聚类是航迹数据分析中的一个重点，通过对记录或实时的航迹数据的聚类分析，可以获得不同空中目标的飞行路径、飞行范围、飞行特征等信息，帮助指挥人员了解空中目标态势，对空情进行指挥或事后研究分析。

以往传统航迹聚类方法，有可以对空间中K 个点为中心进行聚类，对最靠近中心点的对象归类，并迭代中心点位置的K-means 算法。K-means 算法可对圆形或球状的聚类数据进行处理，但无法处理任意形状的数据簇聚类，且需要事先人工设置聚类类别数K，聚类结果也受起始中心点设置的影响。

也有基于网格的移动对象处理算法，将时空域划分为网格，把航迹数据点划分到不同网格内可解决航迹点本身的定位误差，再将邻域密度高于门限的网格连接成簇进行聚类。但对密度不均匀、密度差异大的数据集聚类效果不好，门限参数不好选取，且不能处理空域数据的聚类。

还有基于空间密度的聚类算法DBSCAN，通过统计点迹数据集内任意点邻域内邻近点的数量，不断向邻域扩张聚合为簇，直到遍历所有点完成聚类。同样可发现任意形状的数据聚类，但对密度不均匀、密度差异大的数据集聚类效果不好，且不能处理时空域数据的聚类。

本文使用基于ST DBSCAN 的航迹聚类，既符合DBSCAN 聚类算法的特点和优点又增加了从时间域对目标数据集的扫描。

1 ST DBSCAN 算法

ST DBSCAN 算法的航迹提取实现是在时间域和空间域上对目标点迹进行扫描，以目标航迹点的密度为依据进行聚类。通过此种聚类方式可对任意形状的飞行航迹进行聚类。

1.1 DBSCAN 算法

(1)把所有数据集D 的数据点都标记为无分类标签点；

(2)从任意无标签点开始选取某点p 为扫描的核心点，以核心点p 为圆心，距离邻域Eps 为半径的圆区域Eps(p)为扫描邻域，扫描满足邻近距离门限的邻域点数量；

(3)如果该核心点的邻域点数量小于设定阈值MinPts，则标记该点为噪声点；

(4)如果邻域点数量大于等于设定阈值MinPts，则标记该点p 为核心点，产生聚类编号为簇C1，并将p 在邻域Eps(p)内的点都加入待扫描的簇C1 中；

(5)对簇C1 内的尚未被标记的点重复步骤(2)～步骤(4)的过程，直到簇C1 内的点全部被标记处理；

(6)继续从数据集D 内选取其他未标记过的点，重复步骤(2)～步骤(5)的过程，聚类为另一个新类簇C2、C3等，直到D 内没有未标记过的点。

1.2 ST DBSCAN 算法的改进

ST DBSCAN 算法的改进在于将DBSCAN 算法中的第(2)步加入了对扫描邻域的时间连续性约束，从而可以从时间域维度提高飞机航迹聚类的准确性。具体方法如下：

(1)把所有飞行航迹数据集D 的数据点都标记为无分类标签点；

(2)从任意无标签点开始选取某点p 为扫描的核心点，核心点p 时间邻域ΔT 内为扫描邻域，扫描时间邻域ΔT 内满足以核心点p 为圆心，距离邻域Eps 为半径的圆球区域Eps(p)中满足距离门限的邻域点数量；

(3)如果该核心点的邻域点数量小于设定阈值MinPts，则标记该点为噪声点；

(4)如果邻域点数量大于等于设定阈值MinPts，则标记该点p 为核心点，产生聚类编号为簇C1，并将p 在邻域Eps(p)内的点都加入待扫描的簇C1 中；

(5)对簇C1 内的尚未被标记的点，重复步骤(2)～步骤(4)的过程，直到簇C1 内的点全部被标记处理；

(6)继续从数据集D 内选取未标记过的点，重复步骤(2)～步骤(5)的过程，聚类为另一个类，直到D 内没有未标记过的点。

1.3 参数选取

1.3.1 Eps 值的选取

Eps 的值可通过计算排序K 最近邻距离值获得。

一般情况下，数据集中的噪音点与可聚类数据应该有较大的密度差异才能对不同点迹区分聚类，在K 最近邻距离的排序中K 最近邻距离的值越小说明点迹密度越大，反之说明点迹密度越小。在本文中数据集中，当K 最近邻距离值出现由小到大的明显突变点时，说明点迹的密度从较大的有效航迹区域进入到了密度较小的噪音区域，表明存在一个阈值点可以将数据集的点区分开来。具体的计算方法如下：

(1)K 最近邻距离方法是指对数据集D={p(i)；i=0，1，…，n}内的点，计算出点p(i)到数据集D 内其他每个点的距离；

(2)对距离由小到大排序后得到集合Distance={d(1)，d(2)，…，d(k)，…，d(n)}，其中顺次为k 的距离d(k)就是p(i)的K 最近邻距离；

(3)计算D 中所有点的K 最近邻距离的集合E={e(1)，e(2)，…，e(n)}，对E 中所有距离求均值e′，并计算出各种K 值下e′变化的值，观察变化值最急剧的部分，对应的e′值即为Eps 半径。

1.3.2 MinPts 的取值

MinPts 用来控制聚类簇中点迹的最小数目，可根据聚类簇中点迹的最小可能数进行设置，保证一定有点迹可以完成聚类。

1.3.3 △T 的取值

ΔT 用来控制聚类簇中点迹的最小邻近时间，可根据点迹数据中的最小时间间隔进行设置，保证一定有点迹可以完成聚类。

2 仿真实现

2.1 生成航迹数据

(1)在STK 9 中建立场景产生3 条飞机的航迹；

(2)3 条航迹数据分别导出后使用Python 对数据预处理；

(3)提取3 个航迹文件中的时间以及经纬高数据、添加列名到dataframe 中；

(4)在航迹文件中添加随机噪音数据；

(5)为不同航迹、噪声数据预先打上标签，用于聚类后的结果评估。

组合以上4 组数据并保存为测试数据集。

2.2 航迹数据特征

数据中包含了航迹数据和设置的噪声数据信息(其中经纬高信息使用WGS-84 直角坐标系数值)，并为不同航迹、噪声数据预先打上了标签：航迹1、航迹2、航迹3、噪声，用于聚类后的结果评估，具体如表1 所示。

表1 航迹数据内容

(1)航迹1 与航迹2 在时域的起止点、时间间隔相同，空间域路径无交集；

(2)航迹2 与航迹3 在时间域的起止点不同、时间间隔相同，空间域路径有交集；

(3)航迹1 与航迹3 在时间域的起止点不同、时间间隔相同，空间域路径无交集。

2.3 聚类参数选取

(1)Eps 的取值

根据K 最近邻距离方法，对数据集中航迹点迹的K=2～24 取值时的K 最近邻距离进行顺序排序，可见在K值在3→4、5→6、7→8处的欧式距离值的跳变值都较大，因此以K=3、5、7 时的取值作为Eps 值，分别为5.522、11.251、17.191，具体如表2 所示。

表2 K 最近邻距离

(2)MinPts 的取值

根据聚类簇中点迹的最小可能数设置为2。

(3)ΔT 的取值

根据点迹数据中的时间间隔设置为能包含2 个点迹的时间值0.04 s。

2.4 聚类结果

2.4.1 原始航迹数据

原始的航迹测试数据的三维图中所有的点迹未聚类前的视图，如图1 所示。

图1 原始的航迹测试数据3 维视图

2.4.2 聚类后数据

当选取Eps 值为5.522、11.251、17.191，MinPts 值为2，ΔT 值为0.04 s 时，分别进行聚类处理。得到的聚类结果如图2～图4 所示。

如图2 所示，当取Eps 值为5.522，MinPts 值为2，ΔT值为0.04 s 时，整个航迹点数据集被聚类为了5 类(包括4 类航迹和1 类噪声)，所有点迹的聚类正确率为89.17%。

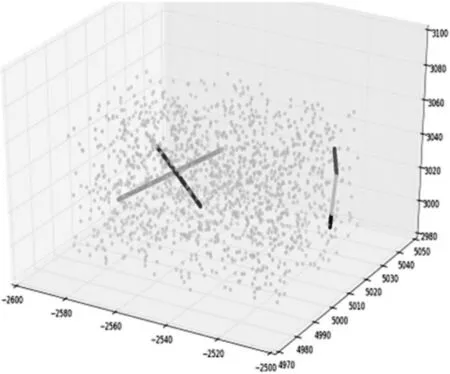
图2 Eps 值为5.522 时的聚类结果

如图3 所示，当取Eps 值为11.251，MinPts 值为2，ΔT 值为0.04 s 时，整个航迹点数据集被聚类为了4 类(包括3 类航迹和1 类噪声)，所有点迹的聚类正确率为100%。

图3 Eps 值为11.251 时的聚类结果

如图4 所示，当取Eps 值为17.191，MinPts 值为2，ΔT 值为0.04 s 时，整个航迹点数据集被聚类为了4 类(包括3 类航迹和1 类噪声)，所有点迹的聚类正确率为100%。

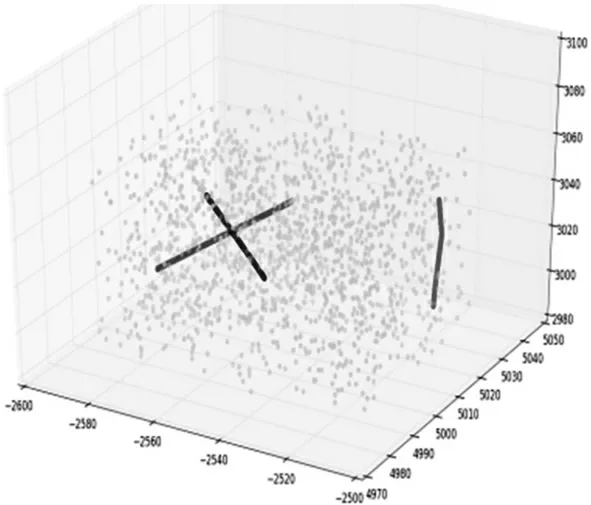
图4 Eps 值为17.191 时的聚类结果

2.4.3聚类结果与分析

根据取Eps 值为5.522、11.251、17.191，MinPts 值为2，ΔT 值为0.04 s 时的3 组参数的聚类效果分析可知，当以距离邻域Eps=5.522 为半径的圆球区域进行扫描时，所有点迹的聚类正确率为89.17%，其中第一类航迹点中有4 484 个由于两点间欧式距离均超过了5.523 因此被聚类为了噪声点，第二类航迹点中有69 个由于两点间欧式距离均超过了5.653 因此被聚类为了噪声点，其余点均聚类正确。

而当以距离邻域Eps=11.251、17.191 进行聚类时，以上航迹中的点均包含在了相应分类的核心点邻域从Eps 为半径的圆球区域内，因此都被正确地聚类，聚类正确率为100%。

3 结论

本文使用一种基于DBSCAN 算法的ST DBSCAN 算法进行了航迹聚类实现，ST DBSCAN 算法既符合DBSCAN 的特点和优点又增加了从时间域对目标数据集的扫描。可对任意形状的航迹聚类，且不需提前划分聚类目标个数，并增加了对包含时空域航迹数据的聚类。通过增加对扫描邻域的时间连续性约束，从而从时间域维度提高了飞机航迹聚类的准确性。通过本文的仿真实现情况，在参数选择合适的条件下可以获得很好的聚类结果。但本方法也有和DBSCAN 相同的不足之处，即对时空间域上密度不均匀、密度差异大的点迹数据集的聚类效果不稳定，且聚类效果依赖对参数的选择等。在未来的工作中可以对此方法进行进一步的优化和完善。