基于量化测量的前向-后向箱粒子平滑器

孙 文

(中国西南电子技术研究所，四川 成都 610036)

0 引言

近年来，对量化测量的关注越来越多[1-5]，正如文献[3]中所指出的，量化是由于通信信道的带宽有限造成的。由于量化测量提供了目标的区间描述而不是点描述，传统的跟踪方法(如常用的粒子滤波)不能直接用于量化测量。在文献[6]中，提出了一种特殊的粒子滤波方法，称作箱粒子滤波算法(Box Particle Filter，BPF)来解决上述问题。其将测量值作为区间，而不是传统的点观测值。BPF 通过引入区间分析方法，为量化测量提供了一种明确的解决方法。近年来，其已经成功地应用于数量可变多目标跟踪[7-8]和扩展目标跟踪[9-10]。

随机评估需要解决三个重要的问题：滤波、平滑和预测[11]，然而过去几年，滤波和预测经常被深入探讨，平滑却经常被忽略。联合延迟观测和平滑对预测性能的改善会超过滤波[12]。对于线性高斯模型，平滑方法是基于卡尔曼滤波框架提出的[11]。对于非线性非高斯模型，平滑方法是通过对粒子滤波进行扩展得到的[13]，或者前向-后向平滑方案[14-16]，或者基于块的粒子方法[17]，或者双滤波平滑器[18-20]。最近在文献[21]中提出了一种具有线性复杂度但不像文献[13]那样受粒子损耗影响的SMC平滑器。

本文提出了一种基于量化测量的前向-后向箱粒子平滑(Forward-Backward Box Particle Smoothing，FB-BPS)算法来解决上述问题，在前向过程中，滤波密度通过标准粒子滤波正向传播给时刻，在反向过程中，根据BPF的相关特征推导出平滑公式[13]。为了进一步提高状态估计精度，提出了一种新的箱形粒子移动步骤。量化测量的仿真结果表明，即使是1 阶(1-Lag)滞后平滑也能显著提高测量精度。

1 背景

1.1 区间分析的基本概念

箱：属于Rn的箱[x]定义为由n(实数)个区间组成：[x]=[x1]×[x2]×…×[xn]，这里实数区间定义为实数集R 上的闭合和连通子集，和分别表示区间[xi]的下界和上界。

区间扩展函数：经过非线性变换后[x]不会总是箱的形式，区间扩展函数f 定义为箱函数[x]的镜像，新的箱函数[f]([x])包含f([x])。

约束：定义H 表示约束满足问题(Constraint Satisfaction Problem，CSP)，H 定义为：H:(f(x)=0，x∈[x])。CSP 的目的是找到属于给定先验域[x]的向量x 集合，满足一组m 约束f=(f1，f2，…，fm)的最佳箱，其中fi是实数函数。该方法确保所有的[x]满足f(x)=0，或者写成S={x∈[x]|f(x)=0}。意味着在H 收敛的情况下，满足约束S⊆[x]T⊆[x]时可以用一个更小的箱[x]T代替[x]，其中[·]T代表向量的转置。一个典型3 维CSP 的例子如表1[22]所示。

表1 典型3 维CSP 示例

1.2 量化测量模型

假设目标的动态函数为：

其中F 是目标的状态转移矩阵，xk是目标在第k 时刻的状态向量，wk是过程噪声。目标的测量可以表示为：

其中，g(·)是测量函数，vk是测量噪声，Δ是量化步进，(·)Floor代表向下取整。

1.3 粒子滤波和箱粒子滤波在量化测量下的比较

根据贝叶斯理论，在[zk+1]状态下xk+1的概率密度p(xk+1|[zk+1])(也称为后验密度)可以通过下式计算得到：

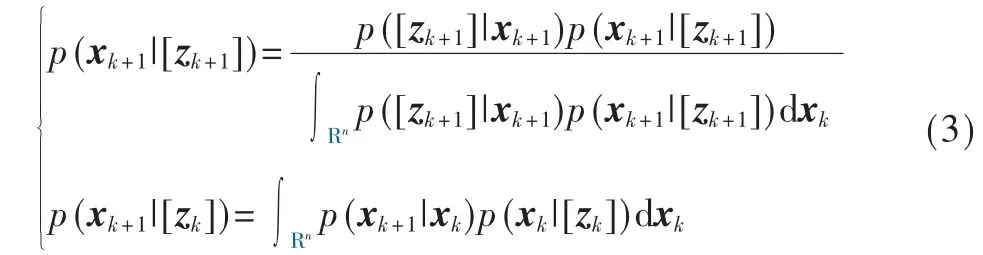
由于量化测量是非线性模型，上述公式没有解析解。广义粒子滤波器[5]可以用来近似估计后验密度，但其计算量是无法接受的。相反在少量粒子的情况下，BPF 的精度优于BF，BPF 和PF 的详细对比如表2 所示。

表2 粒子滤波和箱粒子滤波在量化测量下的比较

其中φ(·)为高斯分布的累计分布函数。

2 箱粒子平滑

前向-后向平滑由前向滤波和后向平滑组成。在前向过程中，滤波密度通过贝叶斯递归向前传递到时刻t。在后向过程中，平滑密度向后传递，从时刻l 到时刻k＜l，通过后向平滑传递。平滑公式如式(5)所示(详细证明见文献[23])：

对于BPF，广义似然函数已经定义了，但是没有考虑f(xk+1|xk)的广义状态转移函数(Generalized State Transition Density，GSTD)。回想一下上述表格中的预测公式），在预测步骤，k 时刻的箱粒子被噪声箱]放大。在约束步骤，重采样、甚至箱粒子中心，受预测过程噪声的影响，箱粒子的边界在预测后会产生移动，导致时刻k+1 的粒子与经目标动态模型预测产生的状态不同。为了正确计算状态转移的概率，将广义状态转移密度函数定义为：

时刻k 箱粒子后验密度与其他滤波器相同，平滑后验也可近似为：

因此，将式(7)带入式(5)可以得到：

表3 所提出箱粒子平滑过程伪代码

在跟踪算法中，估计精度和计算量始终是一对矛盾，BPS 也不例外。随着平滑时间的增加，BPS 的计算量增长趋势非常快，但是精度提升的相对较慢，这一点将在下一节中证实。此外，在文献[23]中，作者从理论上分析了当k=l 时平滑策略注定会失败。这是因为后验p(xk|z1:k)具有特殊的角色，它的特征比其他的分布都好。

在文献[24]中指出，标准FB 平滑具有计算复杂度O(TN2)。这导致PF 无法实现，因为通常使用上千个粒子。但在BPS 中，只有很小的箱粒子(通常不超过30 个)。因此，BPS 跟踪仍然是可行的。

3 实验与结果分析

3.1 仿真场景和算法参数设置

假设匀速直线运动目标初始状态向量为x1=[x，，y，]T=[100 m，10 m/s，300 m，8 m/s]T，其 中(x，)，(y，)分别表示x、y 轴的位置和速度。目标在匀速直线运动上，其状态转换矩阵为：

其中T 是传感器的采样周期。为了简化仿真，这里设置T=1 s，总仿真时间为60 s。在转移函数上加入功率密度σw=3 的高斯噪声。

由于本文考虑的是标准单目标跟踪场景，因此观测噪声均为高斯白噪声，则假设传感器直接观测到目标被高斯噪声污染的位置为x，y，其功率密度为，其中σR=2。点的测量量化步进Δ=5 m。图1 中显示了带有区间和点测量的真实目标轨迹。

图1 具有间隔与量测的真实匀速直线运动目标轨迹

为了全面检验所提算法的性能，考虑30 个箱粒子的BPF、1-Lag BPS 和5-Lag BPS 的跟踪精度，并与广义的PF[5]、1-Lag前向-后向粒子平滑(Forward-Backward Particle Smoothing，FBPS)和带2500个粒子的5-LagFBPS进行比较。FBPS由文献[24]给出，其对早期粒子的顺序更新由核估计代替，并通过快速高斯变换进行。

箱粒子滤波和平滑器的参数设置如下：

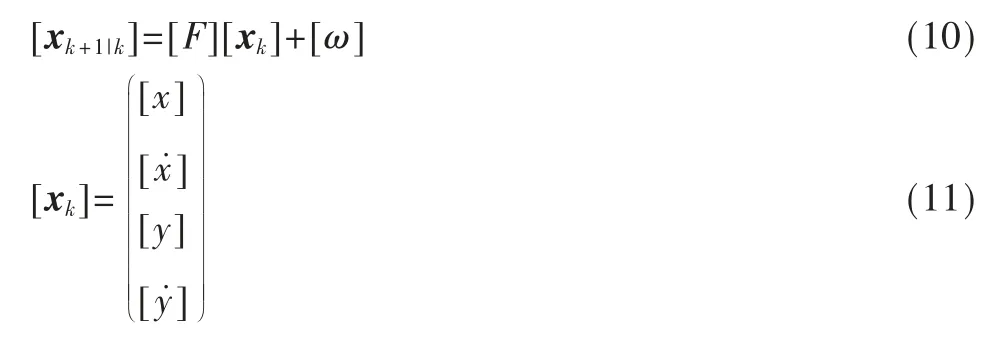
由于F 是线性的，因此[F]=F，这里设置σ=2 m，υ=0.05 m/s。

同样地，设置机动目标的初始状态向量为x2==[300 m，10 m/s，300 m，10 m/s]T，其中，当机动目标做匀速转弯运动时，其状态转移矩阵为：

其中，Fct为匀速转弯运动时的转移矩阵，θ 为转弯速率，由于本文不涉及机动性能较高的目标，因此，在机动目标的运动模型只考虑两种运动方式，分别为匀速直线运动与匀速转弯运动，并且转弯速率取为4°/s 的较小速率，目标状态方程的误差调为σw=5，则带有区间和点量测的真实目标轨迹如图2 所示。

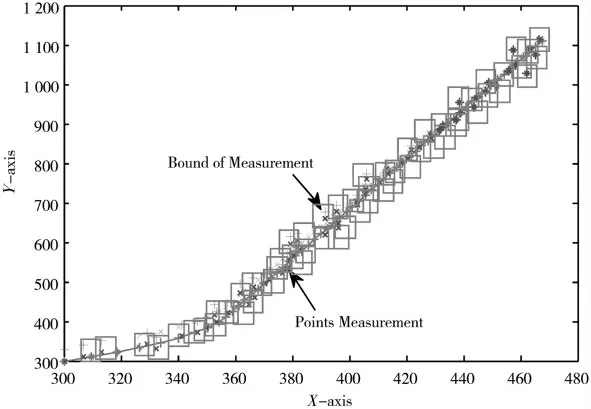
图2 具有间隔与量测的真实机动目标轨迹

3.2 仿真实验对比分析

3.2.1 精度对比分析

在目标作匀速直线运动时，假设轨迹初始算法并不完美，所有的箱粒子和粒子都是从[105 m，9 m/s，295 m，9 m/s]′中采样，这三种算法的递归最小均方估计(RMMSE)如图3 所示，结果在1 000 个蒙特卡罗模拟下。由于5-Lag BPS 需要固定的5 s 延迟，因此结果只显示了1 至65 s的估计。

图3 不同算法下的匀速直线运动目标跟踪RMMSE 对比图

作为结果，可以看到,与BPF 相比，1-Lag BPS 可以实现更好的精度，5-Lag BPS 的精度优于1-Lag BPS，但是在下一小节会看到计算量的增加远大于精度的提升，这可能是在真实应用中不推荐5-Lag BPS 的原因。

当目标为机动目标时，根据图2 仿真的目标轨迹，假设轨迹初始算法并不完美，所有的箱粒子和粒子都是从[305 m，9 m/s，295 m，11 m/s]′中采样，这三种算法的递归最小均方估计(RMMSE)如图4 所示，结果在1 000个蒙特卡罗模拟下。可以看出，算法的性能均有所降低，是由于该算法是在匀速直线运动的目标模型推导出来的，最佳适用匀速直线目标，对于机动能力弱的目标会导致算法性能下降，但未导致曲线发散与算法失效，因此本文提出的算法对机动目标仍为有效。

图4 不同算法下的机动目标跟踪RMMSE 对比图

3.2.2 速度对比分析

针对BPF、1-Lag BPS、5-Lag BPS、PF、1-Lag PS、5-Lag PS 等算法的计算速度问题，本文选用CPU 为i7-6700，主频为3.40 GHz，内存为8 GB 的计算机平台作为试验验证平台，利用MATLAB R2010a 软件验证了各算法的计算速度，具体各算法的运行时间如表4 所示。可以看到，1-Lag 平滑器在跟踪精度方面表现出色，也不会带来巨大计算量的问题。

从表4 中可以看出，5-Lag BPS 计算时间最长，1-Lag BPS 的计算时间比PF 的短，考虑到它们的跟踪精度，可以得出结论：1-Lag BPS 综合性能最好。

表4 不同算法计算时间对比表

4 结论

本文提出了一种基于区间分析和带量化测量的箱形粒子递归的前向-后向平滑算法。它通过加入延迟观测来提高跟踪精度。传统的粒子平滑器只关注粒子权重的更新，相比之下，本文所提出的箱粒子平滑器中的箱粒子会依据最新的观测数据进行移动以接近目标状态的高似然区域，从而进一步提高其性能。结果表明，在不增加太多计算量的情况下，计算精度得到了显著提高。在未来的研究中，将更多的工作集中于在检测前跟踪(Track-before-detect,TBD)框架下研究BPS 的检测特性，以进一步研究其探测特性。