数形结合思想在初中数学教学中的渗透研究

戚方林

【摘要】本文主要以北师大版初中数学教学为例，将促进学生的思维发展和提高学生的数学解题能力作为主要的研究内容，同时通过从数形结合思想的角度出发，借助实际教学案例，分析了初中数学教学中数形结合思想的优势，从而进一步地提高学生的综合素养，提升教师的教学方法以及教学策略，希望能够为同行业工作者提供有效的参考.

【关键词】数形结合;初中数学;教学策略;教学方法

一、引言

在初中阶段，绝大多数的学生已经逐步地养成一定的学习习惯.在传统的数学教学模式之下，我国部分数学教师在开展实际教学的过程中更加偏重于知识灌输和解题技巧的教学工作.随着新课改的不断深入，初中数学知识也从原有的形式上变得更加抽象化和复杂化.在此背景之下，教师通过借助数形结合的教学理念能够将抽象化的数学知识变得更加形象化.此种教学方法在实际使用的过程中不仅能增加学生学习的趣味性，还能化繁为简，从而提升学生的学习效率.

二、数形结合思想的内涵

数形结合思想在实际应用的过程中是把抽象的数字、语言、数学符号和与之相对应的数学图形进行融合，从而在此基础上把数学中的抽象思维转变为一种形象思维.数形结合思想的应用不仅能够拓宽数学教师的教学思路，还能够丰富学生的解题方法.在新的时代背景之下，我国的教育事业经历了数次改革.在新课改的教育背景之下，越来越多的数学教师关注到数形结合思想的重要性.在初中数学教学中，教师借助数形结合思想既能拓宽学生的解题思路，还能提升学生的做题效率.除此之外，在此基础之上，教师还能培养学生的数学学科核心素养.通过把抽象思维与形象思维相结合，教师能够让学生更加直观地理解数学知识中的逻辑性和结构性，有效地掌握数学知识的正确使用方法，从而进一步地强化和提升学生的学习能力和解题能力.

三、数形结合思想对于数学学习的重要性

（一）帮助学生更好地解决数学问题

我们在教学中不难发现，许多初中数学教师在开展实际教学的过程中由于受到了传统教育模式的影响，在课堂教学中仍然以宣讲的模式进行教学.此种教学方式方法使得学生在学习过程中处于被动状态，被动地接受和记忆教材中的相关知识点.然而，初中课程中的数学知识与小学的知识相比更加具有一定的抽象性和复杂性.因此，教师在实际教学过程中如果只是枯燥地讲解，那么很难让学生充分地掌握本节课程中所学的知识.特别是初中的数学知识中涵盖了一些特殊符号以及一些题目代号，这些知识点让学生在学习的过程中很容易出现知识混淆等问题，进而难以解题，总是考不出理想的成绩，从而极大地挫伤了学生的学习积极性.教师借助数形结合思想能够将教材中原有晦涩难懂的数学概念通过直观的图形形式进行讲解，从而能够帮助学生在最短的时间内迅速吸收所学知识，在解题过程中灵活运用，轻松地掌握各种概念.

（二）促进学生形成创新性思维，拓宽学生的解题思路

教师在开展实际教学的过程中要培养学生的发散思维和创新能力.目前，部分初中数学教师在针对知识进行讲解的过程中只知道针对该题型的情况进行分析，而对于题目中所涉及的现实意义没有做过多的讲解.这种情况下就会使得学生只关注到正确的结果，却忽视了解题思路和解题过程的重要性.在这一过程中，学生也没有充分地理解和掌握正确的解题方法.除此之外，教师对于学生发散思维和创新能力的培养有所欠缺，进而使得学生形成了间接的惯性思维.在这种情况之下，教师科学合理地借助数形结合的教学理念将书本知识和日常生活相结合，培养学生的联想能力，强化学生的逻辑思维能力，能让学生在学习知识的过程中快速找到问题的根本所在，在此基础上能够采用不同的方式方法解决同一个问题.

四、数形结合思想在初中数学教学中的具体渗透

数形结合思想主要的实质是数和形之间的转化.由于初中数学知识中的部分内容具有一定的抽象性，教师通过借助数形结合思想能够使学生更加深入地理解所学知识，构建知识体系.除此之外，教师还能对旧的知识体系进行迁移，有效地培养学生的数学思维，促使学生不断地探索数学知识和学习规律，进而在此基础上养成良好的学习习惯，大幅度地提升学生的数学学科核心素养.

（一）数形结合思想在几何图形教学中的渗透

初中数学教材中的几何问题有极大的抽象性，同时是初中数学教学中的重点和难点.因此，绝大多数的学生在解决几何图形问题的过程中较为吃力.因此，为了让学生在学习几何图形的过程中对于相关知识拥有一个更加深层次的理解，初中数学教师在开展实际教学的过程中应尽可能地避免采用纯理论的语句进行讲解，通过科学合理地运用数形结合的教学方式带领学生找到具体的解题思路.

例如，在教学“圆周角和圆心角的关系”这一知识点的过程中，由于垂径定理以及圆周角和圆心角的关系是圆中最重要的内容之一，在中考试题中也经常出现，教师在圆中可以融合三角形、四边形的相關知识，全面考查学生几何方面的知识和能力.在教学过程中，初中数学教师可以采用为学生讲解典型模型、常用辅助线等方法进一步地增强学生的解题经验.初中数学教师借助数形结合思想可以让学生明确顶点在圆上，并且两边都与圆相交的角叫作圆周角.在同圆或等圆中，同弧或等弧所对的角周角相等，都等于这条弧所对的圆心角的一半;在同圆或等圆中，如果两个圆周角相等，那么它们所对的弧长也相等.半圆或直径所对的圆周角是直角，即90°角.90°的圆周角所对的弦是直径.

图1是明清影视城的圆弧形，小红同学到影视城游玩，很想知道这扇门的相对数据.于是，她从景点管理人员处打听到，这个圆弧形所在的圆与水平地面是相切，AB=CD=20 cm， BD=200 cm，且AB，CD与水平地面都是垂直的.请问：这个圆弧形门的最高点离地面的高度是多少厘米？在此题中，教师通过借助数形结合的方法能够让学生将一些晦涩难懂的知识用图形的形式展现出来，从而让学生更好地理解图中的意义和解题方法.E9972EAF-DF16-4739-A4E4-1C9DCA4909E3

（二）数形结合思想在方程求解教学中的渗透

在初中数学的知识点中，方程所占的教学比例相对较大.方程是我国历年各地中考中经常出现的类型题.然而，绝大多数的学生在列方程式的时候很难找到其中数量之间的关系，进而对题目无从下手.为了让学生更加深入地理解方程知识，初中数学教师在开展实际教学的过程中可以潜移默化地渗透数形结合思想，从而让学生更加轻松地理解和运用方程求解的方法.

例如，在教学“一元一次方程”这一内容的过程中，教师借助数形结合的方法能让学生理解一元一次方程的定义，并学会计算一元一次方程，从而为学习一元一次方程的应用打下坚实的基础.又如，在学生理解移项的概念的过程中，教师可以让学生解方程：4x-2=10.方程4x-2=10， 也就是4x=10+2.通过比较这个方程与原方程，我们得知把方程中的-2改变符号之后从方程的一边移到另一边，这种变形叫作移项.

（三）数形结合思想在三角函数教学中的渗透

毫无疑问，三角函数的教学在初中数学数形结合思想的应用中发挥着极其重要的作用.教师通过直接地借助图形的形式来表示线段与线段之间的关系，并且在此基础之上引入正弦、余弦、正切、余切等数学概念表示锐角三角形的数量关系，能够让学生对于三角函数这一知识点形成深刻的认知和理解.教师通过线性关系能够让学生初步地理解正弦、余弦、正切、余切的概念，从而在此基础之上一方面能够培养学生的观察能力和分析能力，另一方面能够提升学生对于几何图形的认知，更加清晰地感知到三角形中角和边之间的关系，帮助学生有效地应用这一关系解决各类不同的题型.教师通过借助数形结合的方法针对初中数学三角函数的关系进行教学，能引导学生利用锐角三角函数从而引出任意角三角函数的定义，同时借助单位圆点的坐标定义三角函数，让学生在此基础之上进一步地探究三角函数和单位圆之间的关系.教师通过借助数形结合思想，根据圆的性质能够让学生更加轻松地理解任意角三角函数的定义及其概念和图形，让他们能够借助三角函数学会描述周期变化规律，从而有效地解决该知识点中的实际问题.

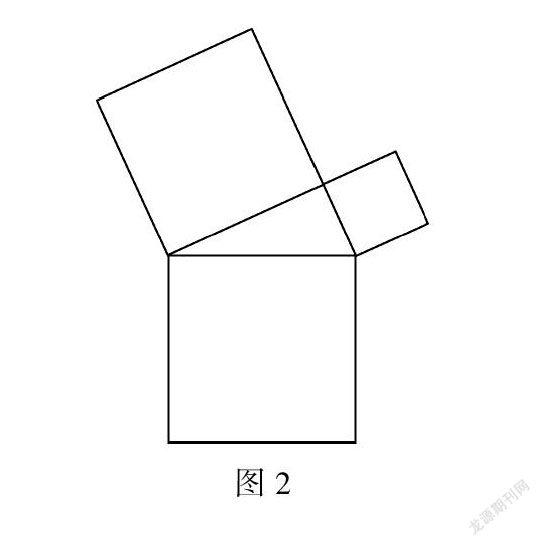
例如，在教学“勾股定理”这一知识点的过程中，教师可以利用数形结合的例题进行引导.

如图2所示：

图2是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案，现在有5种正方形纸片，面积分别是2、3、4、5、6，选取其中三块（可重复选取），按如图所示的方式组成图案，使所围成的三角形是直角三角形.则选取的三块纸片的面积不可以是A.3、4、5，B. 2、2、4， C. 3、3、6，D.2、4、6.通过题意可得，三角形各边的平方是对应的各个正方形的面积，因为所围成的三角形是直角三角形，所以斜边对应的正方形的面积等于两直角边对应的正方形的面积和.又因为3+4不等于5，2+2=4，3+3=6，2+4=6，所以选取的三块纸片的面积不可以是3、4、5，因此选A.

（四）数形结合思想在二次函数教学中的渗透

在初中数学的教学目标中，针对函数这一知识点的教学要求是让学生们能够充分地认知变量、常量以及函数的意义.在这一问题中，二次函数的变量和应变量概念都相对较为抽象，因此，绝大多数的初中生都难以对这一概念进行精准的把握.在这一知识点中，教师通过融入数形结合的思想，能把抽象的、概念性的知识点用图像更加具体和直观地呈现出来，把数所对应的形找出来，借助图像的形式使得学生能够对于二次函数的性质和概念有一个更加精准的把握和理解.初中数学教师在开展实际教学的过程中可以让学生通过自己作图的方式观察二次函数的数学特点.在这之后，教师可以在图像中表现出二次函数所表达的特征，从而帮助学生对二次函数的结论进行深层次的探索，既培養了学生的探索精神和创新精神，又提高了学生的发散思维，更提升了学生的数学核心素养.

例如，在教学“二次函数”这一知识点的过程中，关于二次函数的应用问题，其主要的教学难点是从几何背景及实际情景中抽象出函数模型.在求图形的最大面积方面，教师可以借助数形结合的方法让学生解决实际问题，并且通过观察、比较、推理、交流等过程不断地提升学生的数学思维能力.同时，教师可以引导学生在数形结合的教学方法下积累解题经验，从而发展学生的学习动力.

如图3所示：

在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上，如果设矩形的一边AB等于x m，那么x为多少m时，矩形的面积最大？最大面积是多少平方米？

通过图形，我们可以看出： AB=x m，则BE=（40-x）m.

∵四边形ABCD是矩形，∴AD=BC，AD∥BC，∴∠F=∠ECB，∠A=∠CBE，∴△CBE∽△FAE，∴BC[]AF=BE[]AE，BC[]30=40-x[]40，BC=3[]4（40-x），∴AD=BC=30-3[]4x，y=30-3[]4xx=-3[]4x2+30x=-3[]4（x-20）2+300，∵a=-3[]4<0，图像开口向下，∴当x=20时，y有最大值为300.

即当x为20 m时，矩形的面积最大，最大面积是300 m2.

五、结语

综上所述，在传统的教学模式之下，我国部分的数学教师在开展实际教学的过程中仍然沿用传统的说教式的教学方式和教学方法.随着教育制度的不断改革与优化，以及新课改的进一步落实，初中数学教师应在开展实践教学的过程中将学生作为教学的主体，站在学生的角度出发进行教学.初中数学教师要注重培养学生的数学思维能力和创新能力.除此之外，更为重要的是，教师在教学中还要借助数形结合的教学方式方法将一些难以理解的抽象化的数学知识点和相关概念化繁为简，使学生更加容易地理解数形结合思想的优势.教师借助数形结合思想进行教学能够帮助学生将抽象的数学知识变得更加清晰化、直观化，让学生更加轻松地认识和理解数学知识.同时，教师借助数形结合思想进行教学能够进一步地锻炼学生的创新能力，拓宽学生的数学思路，让学生针对所学知识、学习规律进行进一步的探索，养成良好的学习习惯，从而提升学生的综合素养.这不仅能为我国义务教育阶段的数学教学工作奠定良好的基础，而且能培养出更加全面化的综合型人才.

【参考文献】

[1]尚文斌，聂亚琼.浅谈数形结合思想在高中数学中的应用[J].科教文汇（上旬刊），2008（12）：119，137.

[2]侯丽玲.数形结合思想在小学数学教学中的渗透研究[J].华夏教师，2018（26）：35-36.

[3]李长皞.运用数形结合思想进行概念教学的方法[J].江西教育，2017（15）：82-83.

[4]林丽平.运用数形结合 助力概念教学[J].福建教育，2020（39）：32-33.E9972EAF-DF16-4739-A4E4-1C9DCA4909E3