考虑可变加工次数的多目标阻塞混合流水车间调度
2022-05-31王皓宇
王皓宇
(武汉理工大学 机电工程学院,湖北 武汉 430070)
检测车间一般为混合流水车间,并且不设置中间缓冲区。中间缓冲为零的混合流水车间调度问题也被称为带阻塞混合流水车间调度问题(hybrid flow shop scheduling problem with blocking,HFSP-B),更符合实际的生产环境[1]。随着对流水车间调度问题的研究,近些年有越来越多的文献考虑了更符合实际生产环境的约束。Ribas等[2]使用迭代贪婪算法求解了分布式环境下的阻塞流水车间调度问题,并以最小化总延迟时间为目标。孟磊磊等[3]针对带阻塞限制的混合流水车间调度问题,建立了4种不同的整数规划模型,并用改进回溯搜索算法进行求解。Liu等[4]为有限缓冲的流水车间建立了一个通用模型,模型里考虑了缓冲有限、缓冲为零和无等待3种情况,并提出了一种结合问题特征的启发式算法。轩华等[5]将有限缓冲的混合流水车间调度转换为带阻塞的混合流水车间调度,并混合了遗传算法和禁忌搜索对问题进行求解。
车间调度通常涉及多个目标同时优化,其结果往往不是一个最优解,而是符合Pareto最优解概念的一组解[6-7]。目前有大量文献致力于研究一种高效的算法来求解多目标车间调度问题。蒋增强等[8]使用血缘变异对非支配排序遗传算法进行改进,并考虑了能源消耗、最大完工时间、加工成本和质量成本4个目标。Wang等[9]使用NSGA-II(non-dominated sorted genetic algorithm-Ⅱ)算法求解了不确定加工时间条件下的流水车间调度问题,并加入了局部模拟退火算子和与场景相适应的邻域搜索算子。Gong等[10]考虑了阻塞和分批两个约束,以最小化最大完成时间和总提前时间为目标,使用人工蜂群算法求解。
笔者在HFSP-B模型的基础上,根据现实生产环境,考虑了加工次数对加工效率和加工合格率的影响,以最小化最大完成时间和最小化总质量成本为目标展开了研究。
1 问题描述和建模
1.1 问题描述
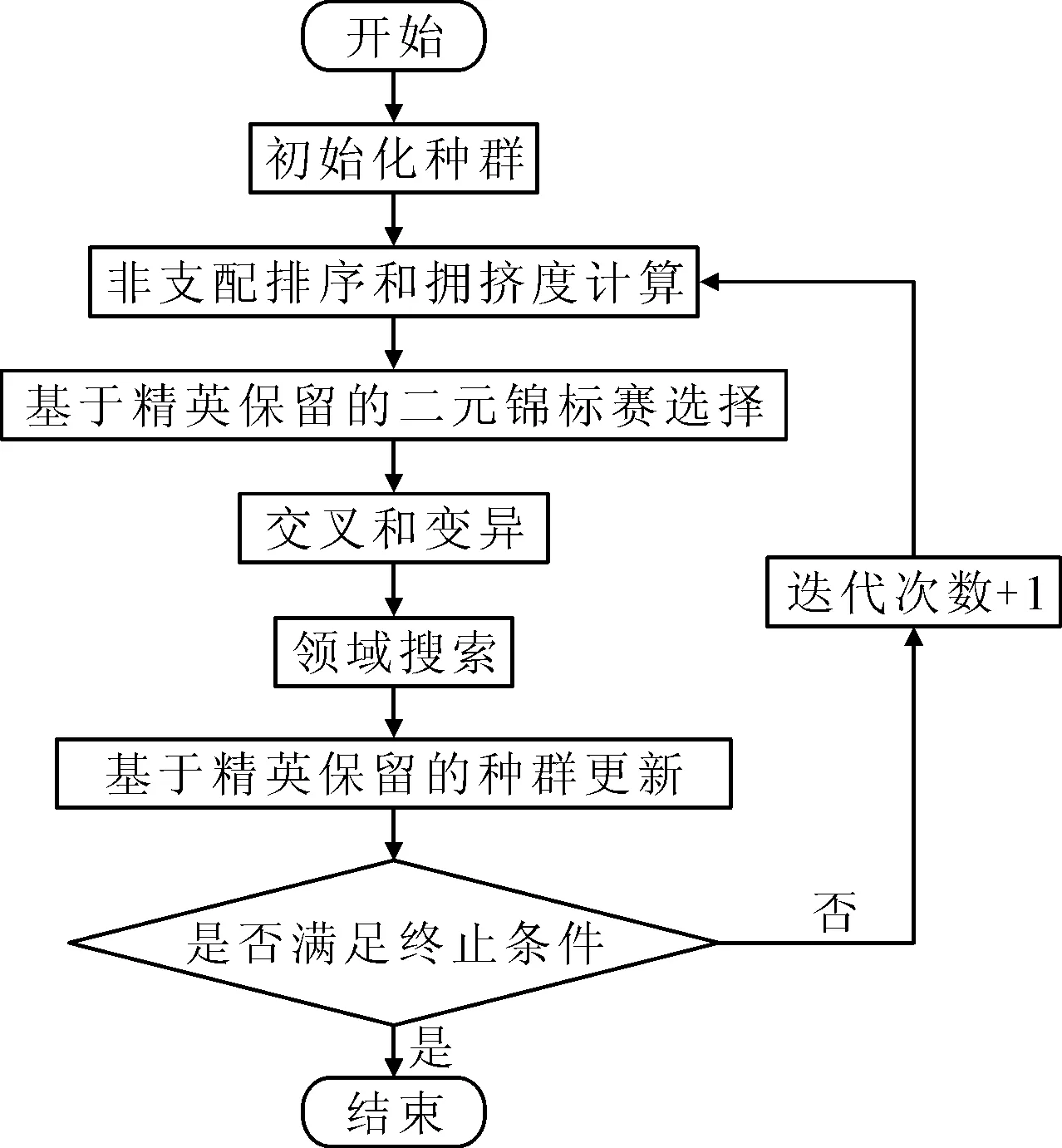
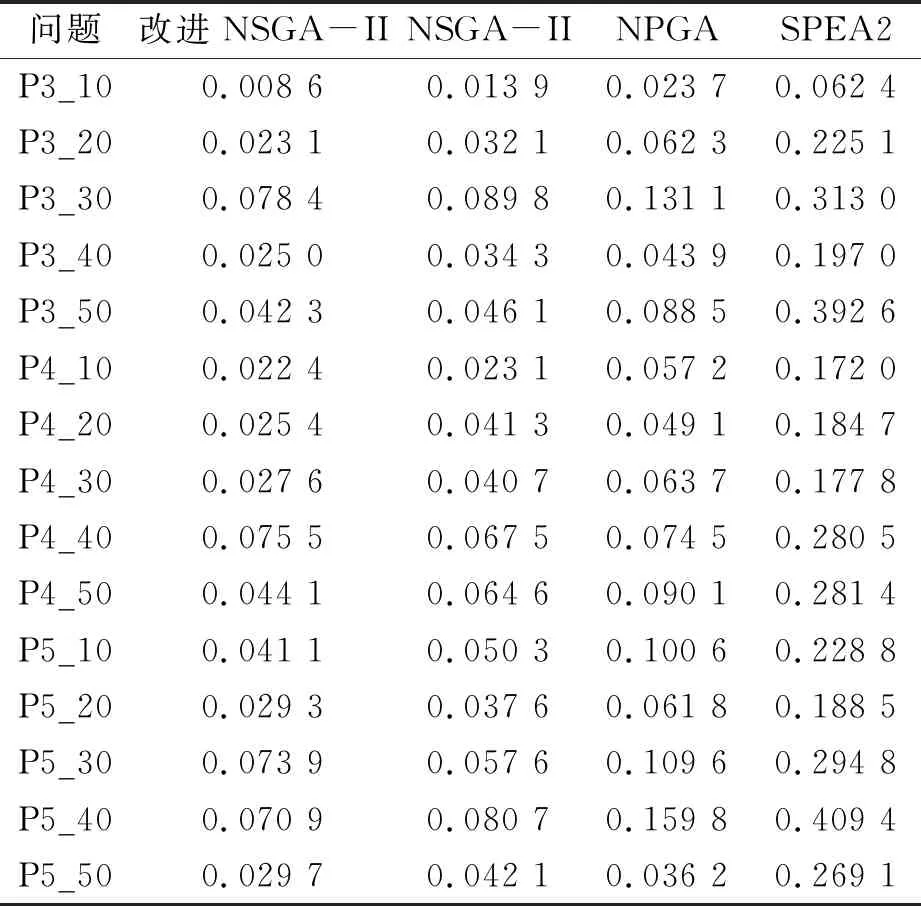
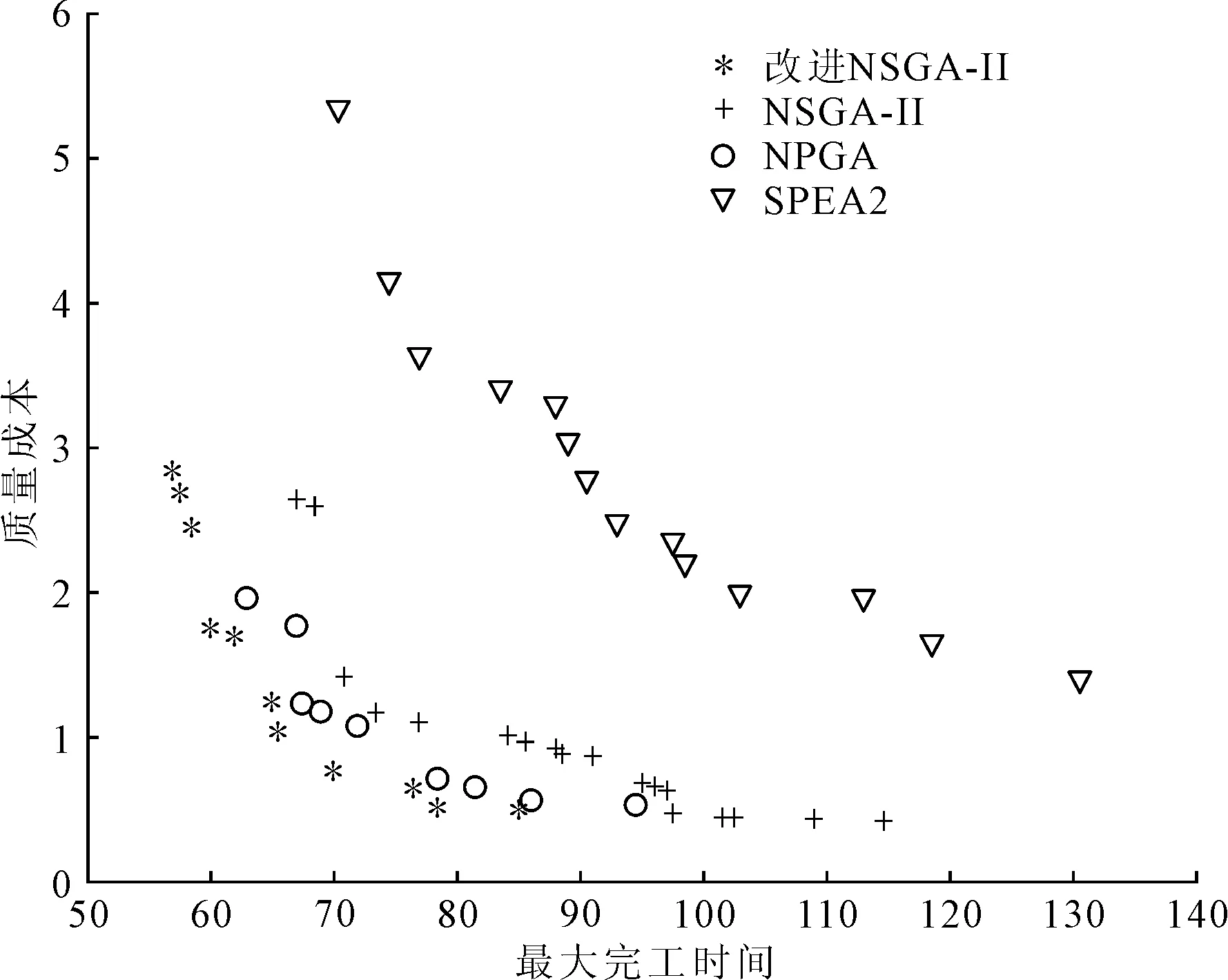
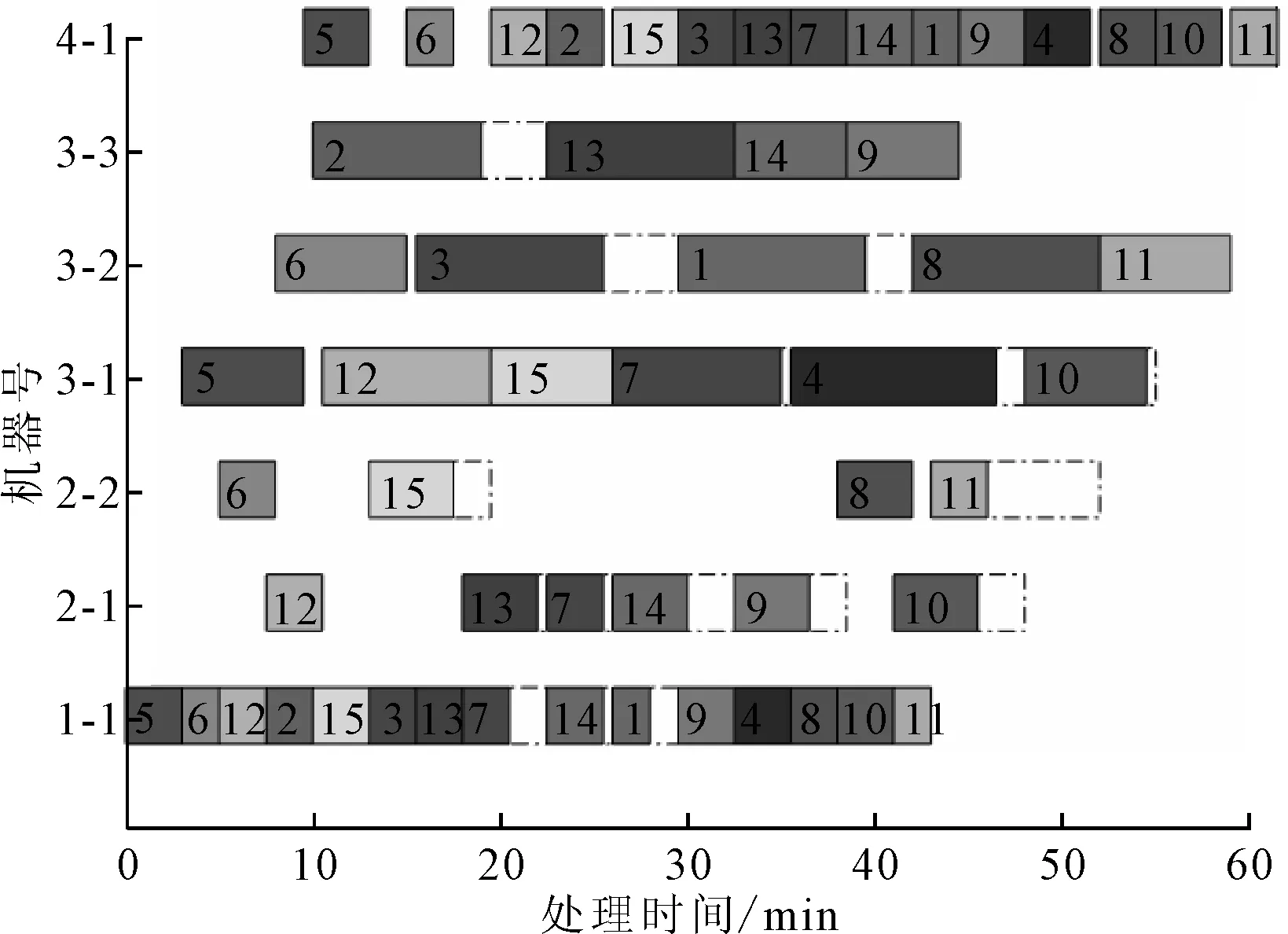
考虑质量成本和加工次数的HFSP-B描述如下:混合流水车间由m个阶段串行组成,阶段i(i=1,2,…,m)有ni个相同的并行机,ni≥1且至少存在一个阶段使得ni>1。每个工件必须在其路径上的每个阶段选择一台机器进行加工。Pik表示工件k(k=1,2,…,p)在阶段i的加工时间。工件k在阶段i的完成时间被记为Cik,并且Dik是它在阶段i的离开时间。加工过程不能被打断意味着工件k在阶段i的开始加工时间Sik为Cik-Pik。工件k在阶段i完成后,需要其在阶段i+1分配的机器可用时再离开。如果在Cik时刻,工件k在阶段i+1分配的机器被占据,那么其会被阻塞在当前阶段的机器上,直到Dik=Si+1,k,如图1所示,图1中的斜线部分表示阻塞状态。另外,至少存在一个阶段,其并行机加工工件的合格率存在差异,Qijk表示阶段i的机器j(j=1,2,…,ni)在加工工件k时的质量成本,0 图1 阻塞机制 建立一个以最小化完成时间和总质量成本最小为目标的带阻塞混合流水车间调度问题模型,其中的符号含义如表1所示。 表1 模型符号及说明 优化模型为: f1=minCmax,k=1,2,…,p (1) (2) Cik=Sik+Pik,i∉S,k=1,2,…,p (3) Cik=Sik+Pik+EPik,i∈S,k=1,2,…,p (4) Sik≥Ci-1,k,i=2,3,…,m,k=1,2,…,p (5) Dik=Si+1,k,i=1,2,…,m-1,k=1,2,…,p (6) (7) yikk′+yik′k≤1,i=1,2,…,m, k=1,2,…,p,k′=1,2,…,p,k≠k′ (8) Sik′≥Dik+L×(3-yikk′-xijk-xijk′), i=1,2,…,m,k=1,2,…,p,k≠k′ (9) 其中,Cmax为最大完工时间,式(1)为最小化最大完工时间;式(2)为最小化总质量成本;式(3)和式(4)为处理过程不允许被打断;式(5)为工件只能在一道工序完成后才能开始下一道工序;式(6)为阻塞关系,只有当工件的下一道工序可以被加工时才允许离开当前机器,否则会被阻塞;式(7)为每个工件在每个阶段只能选择一台机器;式(8)和式(9)为每台机器最多同时处理一个工件。 笔者提出了一种改进的NSGA-II算法来求解上述问题。改进NSGA-II的流程如图2所示。这些改进的程序主要包括:编解码规则,精英保留机制,多种遗传算子,以及邻域搜索策略。 图2 改进NSGA-II算法流程图 在将改进NSGA-II算法应用于问题求解之前,编码是一个非常重要的部分。本文的多目标调度不仅需要同时处理工件的输入序列和每个阶段的机器分配,并且还要决定工件的加工次数。因此,笔者提出了由序列向量X、分配矩阵Y以及次数矩阵Z3部分组成的染色体结构。其中,向量X决定了工件的输入序列,矩阵Y决定了每个阶段工件分配的机器,矩阵Z决定了工件在有质量差异的阶段S中需要额外加工的次数。图3为一个3阶段4工件的解的染色体表达式,阶段S={3}可以进行多次加工。 图3 一个解的染色体表达 交叉是种群进化的基本方式,通过交换两个父代个体中的基因来获得新的个体。鉴于本文的染色体由3部分组成,这里选择3种不同的交叉方式,各部分根据交叉概率Pc决定是否交叉。对于输入序列部分,选择的是基于顺序的交叉(order crossover, OX),即随机产生两个交叉点,将其中一个父代的中间部分复制给子代,然后根据另一个父代的基因顺序补齐剩余基因。对于机器分配部分,则选择部分匹配交叉(partial-mapped crossover, PMX),即随机产生两个交叉点,交换中间部分的基因片段。对于额外次数部分,采用的是基于位置的交叉(position-based crossover, PBX),首先随机选择多个基因位,然后交换这些基因位上的基因。 变异是保持种群多样性的基本方式,通过改变、插入或重组个体中的基因来产生新的个体。本文对序列向量部分采用的是重组变异,首先随机选择两个变异点,然后逆序排列中间的基因片段。其余部分采用多点变异,对存在多种选择的基因位上的每个点以变异率Pm进行判定,改变后的基因码要与原来的值不同。 邻域搜索是对NSGA-II算法在局部搜索能力上的补充,是一种主动寻找更优解的策略。为了不破坏解的特征,邻域搜索应该发生在一个较小的范围。根据解的染色体表达方式,制定了3种邻域结构。 (1)针对输入序列部分,采用插入的方式搜索邻域。首先随机选择一个基因位,将该基因随机插入到其他位置。 (2)针对机器分配部分,采用重组的方式,随机交换各产品选择的机器。即首先随机选择一个存在并行机的阶段,然后对该阶段机器码中的基因片段进行随机排列。 (3)针对额外次数部分,邻域搜索朝着两个方向进行,即增大和缩小加工次数。具体操作为随机选择一个不为最大值的基因位和一个不为0的基因位,分别使该基因位的值加一和减一。若所有基因位均为最大值,则只执行减一操作,若所有基因位均为0,则只执行加一操作。 在经过遗传操作和邻域搜索后,首先需要剔除重复个体,保证种群的多样性。然后判断当前个体数量和种群规模的大小,如果小于种群规模,则加入扰动种群,即通过初始化的方式随机产生个体使个体数量达到种群规模;如果大于种群规模,则通过非支配等级和拥挤度进行排序,剔除超出种群规模的个体。 通过实验研究评估所提出的改进NSGA-II算法在处理问题时的性能。所有算法都通过Matlab编程,运行在一台Windows 7操作系统,Inter core i7,2.39 GHz,8 GB RAM的个人计算机上。 随机产生了15种测试数据集,问题的大小由工件数和阶段数决定,阶段数m=[3,4,5],工件数p=[10,20,30,40,50]。每个阶段的机器数量在1~4中随机产生,并确保至少有一个阶段存在并行机,工件在每个阶段的加工时间PT服从4~9的均匀分布,随机产生部分可多次加工的阶段,每次额外加工时间EPT=0.8PT,质量成本Q服从0~1的均匀分布。 为了验证提出的改进NSGA-II算法在求解阻塞混合流水车间调度问题时的有效性,笔者将其与NPGA(niched pareto genetic algorithm)算法、SPEA2(strength pareto evolutiorary algorithm 2)算法及改进前的NSGA-II算法比较。这些算法的参数设置为种群规模50,迭代次数200,交叉率0.9,变异率0.1。为了评估多目标算法的帕累托前沿,采用了反世代距离(inverted generational distance, IGD)指标。每个数据集运行10次,取这10次结果IGD的平均值展示在表2中。从表2可知,所提出的改进NSGA-II算法在求解大部分问题时IGD明显小于其他算法,说明其拥有更好的收敛性和多样性。与改进前的NSGA-II算法相比也具有较大的优势,这说明对算法的改进是有效的。 表2 实验结果的IGD评估 图4为一次实验中各算法最优结果的Pareto前沿,从图4可知,所提出的改进NSGA-II算法获得的非支配解更靠近图形的左下方并且分布的范围较广,说明其获得的非支配解相比其他算法获得的解质量更好。图5为由改进NSGA-II算法求得的一个非支配解解码得到的甘特图,图5中的虚线框表示机器处于阻塞状态。 图4 各算法的帕累托前沿 图5 一个非支配解的调度图 以带阻塞的混合流水车间调度问题为基础,考虑了允许通过多次加工来提高加工质量的情况,以最小化最大完成时间和总质量成本为目标建立了问题模型。提出了一个改进NSGA-II算法来解决这个实际问题。提出的改进NSGA-II算法主要包括结合问题特征编码,多样的遗传操作算子,与染色体结构相适应的领域搜索以及添加扰动种群。通过随机生成的案例进行测试,验证了所提出的改进NSGA-II算法的效率。与NPGA、SPEA2算法进行了比较,结果显示在大多数情况下,所提出的改进NSGA-II算法表现更佳。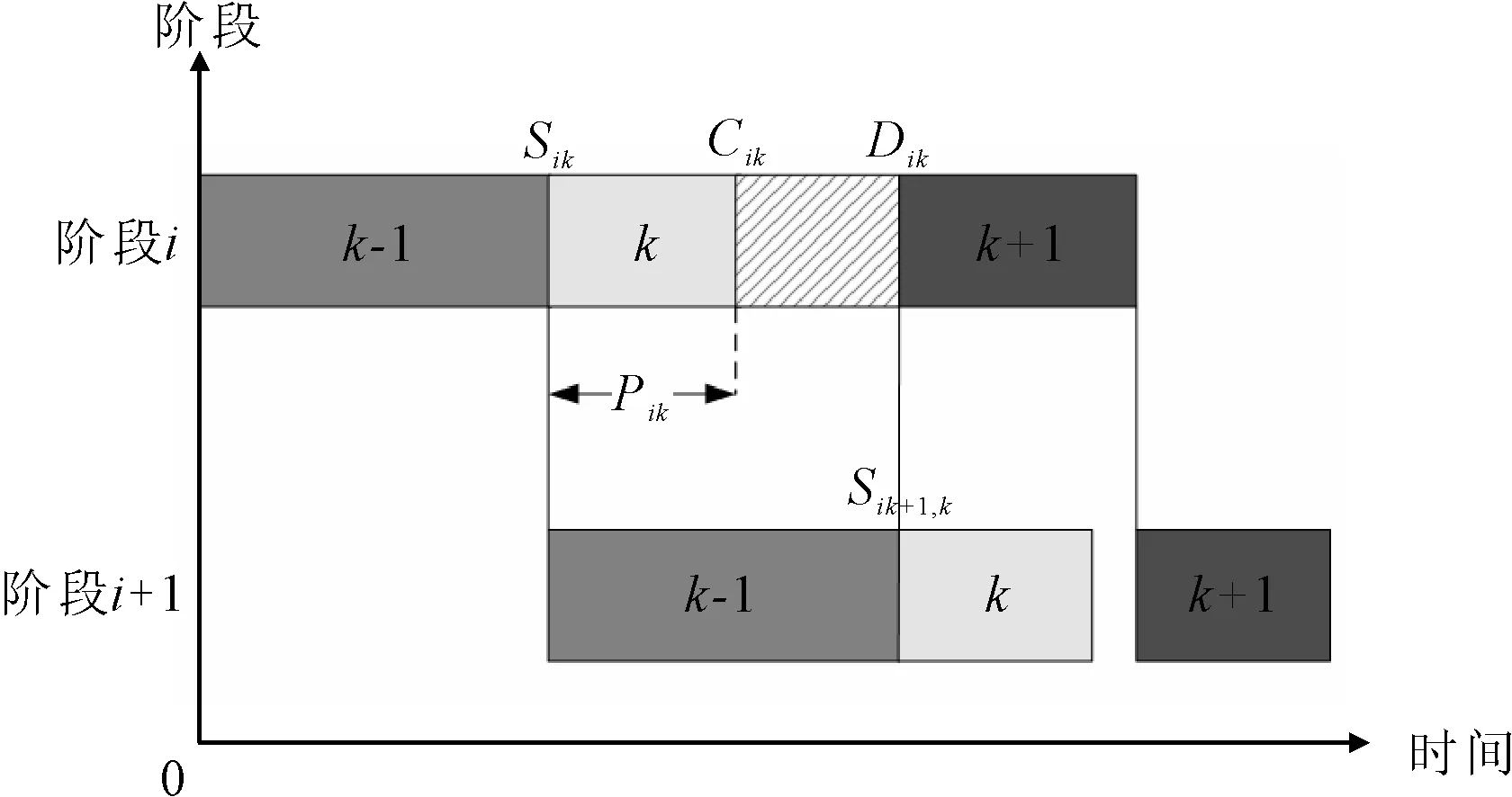
1.2 调度模型

2 改进的NSGA-II算法
2.1 染色体表达

2.2 交叉与变异
2.3 邻域搜索
2.4 产生新种群
3 实验研究
4 结论
