基于Hadoop的高压输电线路合闸故障诊断方法
2022-05-31朱晗雨
周 晓,朱晗雨
(武汉理工大学 机电工程学院,湖北 武汉 430070)
高压输电线路电力故障诊断主要是指通过线路状态信息进行分析判断准确识别故障类别[1],而高压输电线路合闸故障诊断对于整个电力系统能够稳定运行具有重要意义,该技术不仅能够降低电网运行风险,满足日常用电需要,也提升了高压输电线路的可靠性[2]。目前,高压输电线路合闸故障诊断方法有基于信号分析技术的方法以及基于数据挖掘技术的方法等。
基于信号分析的电力系统故障诊断技术主要通过小波变换(wavelet transform, WT)和S变换等传统方法对电力波形进行分解,并在此基础上根据数据特点进行优化从而实现故障诊断的目的。基于小波变换的故障诊断方法[3-4]首先将采集到的电力波形数据进行小波分解,提取到波形信息的高频小波系数,然后分析小波系数从而预测系统的故障时间点,然后结合故障发生的时间点,采用基于模极大值的奇异性检测方法分析系统的故障位置,该方法对于暂态信号的处理效果较好,但是难以选取合适的小波基函数。基于S变换的故障诊断方法[5]通过获取的时频特性和系统状态信息熵进行电力系统故障诊断,该方法对系统的变化敏感度高,抗干扰能力强,但是对于高频信号的分析能力不如小波变换。
数据挖掘技术利用各类机器学习算法分析高压输电线路合闸故障数据从而实现故障诊断的目的,目前围绕数据挖掘技术开展研究的方法主要分为有监督学习算法和无监督学习算法。文献[6]提出了一种基于Logistic回归深度学习的故障诊断模型,解决SCADA(supervisory control and data acquisition)系统中故障诊断标准模块误报率过高的问题。文献[7]使用贝叶斯网络依据历史数据库中的真实数据对模型进行训练,完成了电力系统故障的诊断研究。文献[8]提出了基于自适应神经模糊推理方法的光伏发电站模块故障诊断方法。
由于电力负荷数据量爆炸性增长,数据特征关系极其复杂,以往的统计学分析以及数据挖掘技术已经无法满足当下的高压输电线路故障数据分析要求。伴随着大数据技术的高速发展,陆续出现了各种各样的大数据处理框架如Hadoop、Spark和Flink[9-10]。这些大数据处理系统提供了可靠、稳定的数据分析流程,为大规模的电力系统故障诊断分析提供了有利的工具。文献[11]通过构建基于大数据的电力计量装置解决了传统电力计量智能诊断方法效率低下,准确性不高的问题。文献[12]搭建Hadoop大数据处理分析平台,结合MapReduce并行式计算框架的特点设计了PCA-SVM(principal component analysis-support vector machine)算法,实现了基于数据的高压输电线路合闸故障诊断。文献[13]设计了一种基于大数据分析平台的聚类算法,该方法根据未标记的数据自动选择聚类值,解决了输电塔故障预测的问题。目前依靠成熟的大数据技术可以对海量电力数据进行挖掘从而精准定位故障类别。
笔者以高压输电线路合闸故障数据为分析对象,着重分析挖掘数据中隐含的规律,通过多种数据特征提取策略对数据进行处理,并结合数据具有连续性、时序逻辑性等特点提取数据特征并构建故障数据集,然后利用遗传算法改进的K-means算法进行高压输电线路合闸故障诊断。在此基础上,通过Hadoop并行式计算框架对算法进行加速,通过并行计算的方式解决算法在高压输电线路合闸故障数据量较大的情况下收敛速度慢的问题。
1 高压输电线路合闸数据特征工程
高压输电线路合闸状态数据通过故障录波器实时监测故障前后时刻的电力负荷状态,采集该信息并以时间序列的形式存储在数据库中,以时序波形信号存在的电力数据中蕴含了大量有价值的信息[14],但是通常都无法直接利用机器学习的方法对其进行分析,而且故障录波器采集到的数据通常存在各种噪声,若不进行特征提取直接通过机器学习算法进行数据挖掘,得到的结果往往也不尽人意,因此需要对波形信号进行特征工程和预处理操作,具体流程如图1所示。

图1 特征工程流程示意图
1.1 数据滤波
真实工况下的电力信号由于周围环境的影响在采集的过程中可能会携带大量噪声,这对于后续信号特征提取会有极大的负面作用。因此对信号进行噪声滤波处理是必要的,通过滤波能够将有用信号与噪声分离提高信号的信噪比,并提升分析精度。笔者通过使用算术平均滤波法对原始信号进行滤波处理,滤波效果如图2所示。

图2 窜入波形滤波对比示意图
1.2 分段信息提取
根据故障类型的不同可以将数据分为两个大类,分别为两段式波形和三段式波形。为了使特征提取过程中得到的特征属性更能反映故障发生时刻前后的波形变化,设计了一种分段信息提取方案,将每一条样本数据划分为5段,分别是波形起始阶段、故障发生时刻前、故障发生时刻、故障时刻后与波形结束阶段。第一段长度为2周期;第二段长度为2周期;第四段长度为2周期;第五段长度为2周期;第三段为不包含以上4段的所有周期内的数据,周期长度依据数据采样率而定,如图3所示。
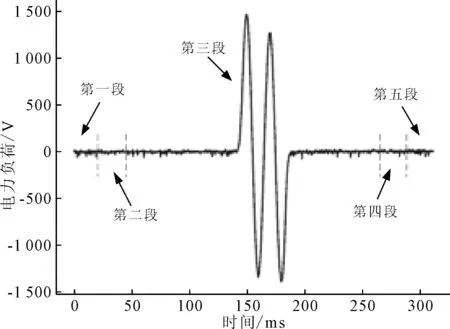
图3 波形分段示意图
由于每种类型的故障在某个时间段的波形特点都与其他类型不同,因此图3所示的分段提取特征方式能够有效地将各类合闸故障区分开。
1.3 时频域特征提取
时域分析是对以时间序列表示的信号进行信号提取、波形特征计算的信号处理方法,常用的时域故障特征参数有均值、方差、波形指标等。频域分析法是研究控制系统的常用方法,频率特性表示不同函数对于系统输入输出的影响程度。时频域特征提取过程获取的特征值包含各类故障数据的特点,为故障诊断提供了有效信息,同时也为数据样本集的构建提供了数据支撑。图4为时频域转换对比图。
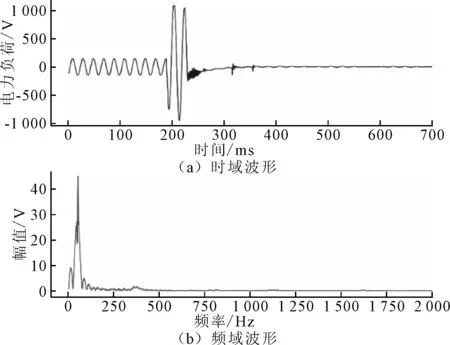
图4 时频域转换对比图
2 基于K-means的高压输电线路合闸故障分类
2.1 基于K-means的故障分类流程
传统的K-means算法是无监督的聚类算法,算法原理是基于数据样本集,按照样本之间的距离将数据集划分为不同的簇,划分的原则是让簇内的点紧密靠近,簇与簇之间则最大程度分散。假设簇划分为(c1,c2,…,ck),则算法的目标是最小化平方误差E,其计算公式为:
(1)
式中:xi为第i个样本;μi为ci的质心;k为聚类数。
(2)
K-means算法在执行前需要确定k,该值的变动对算法最终结果影响较大。通常使用该算法进行数据分析时,k值都是依靠研究人员对数据的经验或者交叉验证方法来确定。在确定k之后,还需要选择k个初始聚类质心,若聚类质心选择不当也会对结果产生较大影响。这种随机取值方式会造成极大的误差,因此,笔者利用遗传算法的自动寻优特性对K-means算法进行优化。
2.2 基于遗传算法的K-means诊断算法优化
遗传算法(genetic algorithm,GA)求解问题时,问题的每一个可能解都会被编码为一条“染色体”,也可以称为个体,若干个体构成群体。算法初始阶段,会随机产生一些初始解,计算每一个个体的适应度值,该值是算法迭代的关键。笔者采用的遗传算法步骤如下:
(1)编码方式。染色体的基因编码用初始聚类质心在数据集中的编号表示,每个染色体代表一个可行解,染色体长度为聚类数量,例如染色体{2,4,9,12,15,20,70,90,130}表示编号为2、编号为4、编号为9、编号为12、编号为15、编号为20、编号为70、编号为90以及编号为130的样本被选定为中心。
(2)适应度函数。由于本文采用遗传算法是对K-means做优化改进,而K-means算法的最优结果具有相同类别的数据紧密,不同类别的数据松散的特点,因此设计了如下适应度函数:
(3)
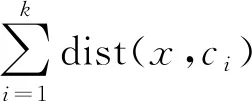
(3)选择算子。采用轮盘赌的方式对个体的适应度函数值度量的优劣性进行判断,该个体在下一代中是否该淘汰。适应度较大的个体存活几率较大,适应度较小的个体在迭代结束后被淘汰的机率较大。选择概率的计算公式为:

(4)

(5)变异算子。通过变异概率改变个体基因,从而形成新个体。
基于上述步骤,笔者设计的基于遗传算法的初始聚类质心寻优主要流程如图5所示。
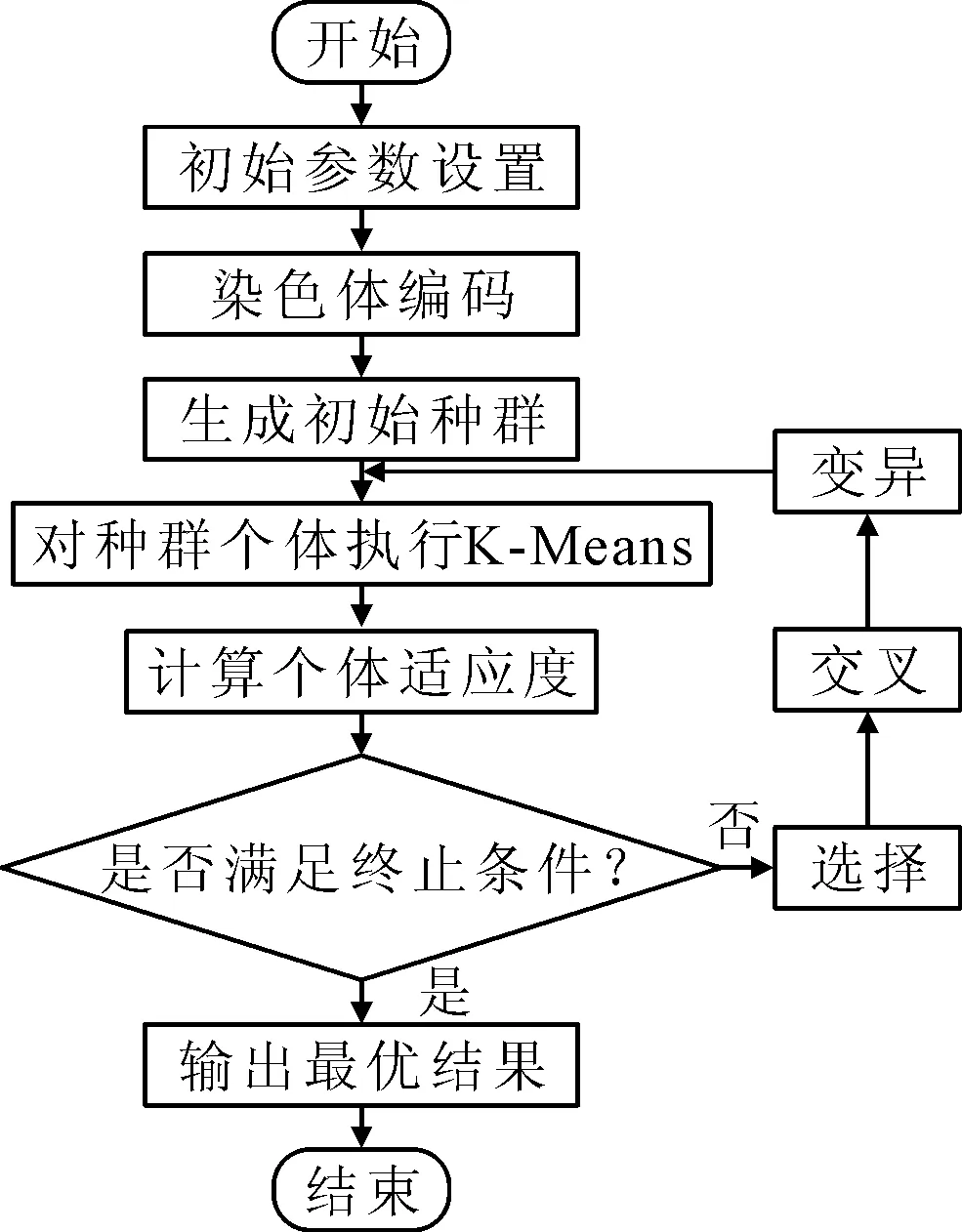
图5 基于遗传算法的初始聚类质心寻优流程图
基于遗传算法的初始聚类质心寻优步骤如下:
(1)确定算法初始值,主要包括种群内个体数量p,一般取20~100,最大遗传迭代次数N,一般取100~500,交叉概率pc,一般取0.4~0.99,变异概率pm,一般取0.001~0.1以及最优解的适应度阈值θ;
(2)初始化种群,首先在样本集中随机选取9个样本作为初始染色体的等位基因编码值,重复该操作p次,生成初始种群;
(3)对种群中的每一个个体进行K-means聚类,并根据适应度函数评价聚类结果适应度;
(4)判断结果是否满足最大迭代次数或最优解的适应度函数值是否超过阈值θ,若不满足则进行选择操作、交叉操作、变异操作、产生新种群,并重复执行步骤(3);若满足则输出最优结果。
2.3 算法并行化设计原理
通过Hadoop平台对算法进行加速处理,需要算法与MapReduce并行框架相结合。笔者设计的GA-K-means聚类算法本质是一个两段式求解问题,首先通过遗传算法自动获取到最优的初始聚类质心,然后通过该质心进行正常的K-means聚类。因此通过Hadoop平台对遗传算法和K-means算法进行加速优化的过程主要分为两步,首先针对遗传算法进行并行化设计,在保证算法运行效率的前提下获取最优的聚类质心,在此基础上针对K-means算法进行并行化设计,得到最终的高压输电线路合闸故障聚类结果。
2.4 遗传算法并行化设计
在进行遗传算法并行化设计的过程中,需要将迭代过程根据MapReduce框架特点设计为任务流的形式。图6为遗传算法并行化流程图。
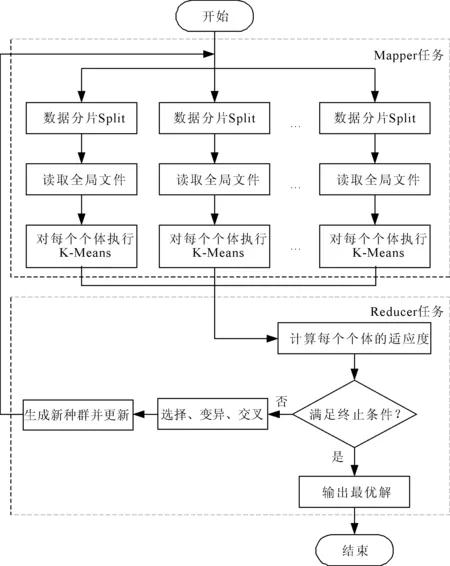
图6 遗传算法并行化流程
遗传算法的并行化流程如下:
(1)Mapper任务设计。设置Map任务数量,读取全局初始质心文件。输出自定义数据格式:Mapper任务通常以
(2)Reducer任务设计。Reducer函数首先将各个Mapper任务执行完成的结果拉取到本地节点中,以Mapper任务输出的数据格式进行解析并执行个体的适应度计算。然后根据函数终止条件判断是否输出最优结果,如果当前结果不满足终止条件,则对个体进行选择、变异、交叉操作,产生新种群并将新种群的所有个体信息更新到全局文件中。
2.5 K-means算法并行化设计
由并行化遗传算法计算得到的最优初始聚类质心,基于此质心对所有的高压输电线路合闸故障特征数据进行并行化K-means聚类。图7为并行化K-means算法流程图。

图7 K-means算法并行化流程图
针对K-means算法的并行化设计主要分为Mapper部分和Reducer部分,在提交任务之前首先初始化算法运行参数,包括最大迭代次数N,误差阈值σ。
(1)Mapper任务设计。每个Mapper任务会读取不同的数据切片以及全局初始聚类质心,针对读取到的每一个数据样本进行一次距离计算并划分到距离最近的样本点所属类别中。当Mapper任务内的所有数据都完成计算之后,将聚类得到的类别与数据信息封装为符合Mapper输出要求的数据格式,如<聚类类别,数据信息>的键值对形式。
(2)Reducer任务设计。在优化聚类质心的迭代过程中,每一个Reducer任务会将所有Mapper任务的输出拉取到本地节点中进行计算。通过<聚类类别,数据信息>的形式解析每个类别的数据量大小并以此为基础进行误差计算,判断当前的质心是否满足了迭代终止条件,如果不满足条件则更新质心并将新的聚类质心结果写入到全局文件,然后开始下一轮迭代任务;如果满足迭代条件,则终止迭代任务,直接执行最终的聚类任务。
3 实验设计与分析
实验主要是对比分析基于K-means算法的故障诊断方法以及笔者提出的GA-K-means算法,然后分析优化改进后的并行化算法相较于串行算法的加速性能。笔者使用的实验数据来自于各地高压输电线路合闸实时数据,一共有9种故障类型,数据样本如表1所示。

表1 高压输电线路合闸故障数据样本
3.1 基于K-means的故障诊断试验
为了对所提出的基于K-means的高压输电线路合闸故障的有效性进行验证,笔者在硬件环境为Inter(R)Core(TM)i5-8300H CPU@2.30GHz, 16 GB 内存,软件环境为Python 3.6 的机器上进行实验。本次实验分为3个部分,分别是基于K-means算法的高压输电线路合闸故障分类实验、文献[15]设计的DGK-K-means算法以及笔者设计的GA-K-means分类算法。
实验一使用传统的K-means算法对上述数据集中的训练集进行聚类,初始参数设置:最大迭代次数Maxgen=200,最小误差σ=0.01;
实验二使用DGK-K-means算法对训练集进行聚类,该算法利用高斯核密度确定初始聚类质心。初始参数设置:平均类内最大相似度AMS为20,终止条件为AMS≤4;
实验三使用GA-K-means算法进行聚类,遗传算法初始参数设置为:最大迭代次数N为200,种群内个体数量p为30,交叉概率pc为0.7,变异概率pm为0.08;K-means算法初始参数设置为:最大迭代次数Maxgen为200,最小误差σ为0.01。
每个实验得到最终的算法模型后在相同的测试集上进行准确率测试,每组实验分别重复运算3次,然后取3次的准确率均值比较3个算法的性能,测试结果如表2所示。
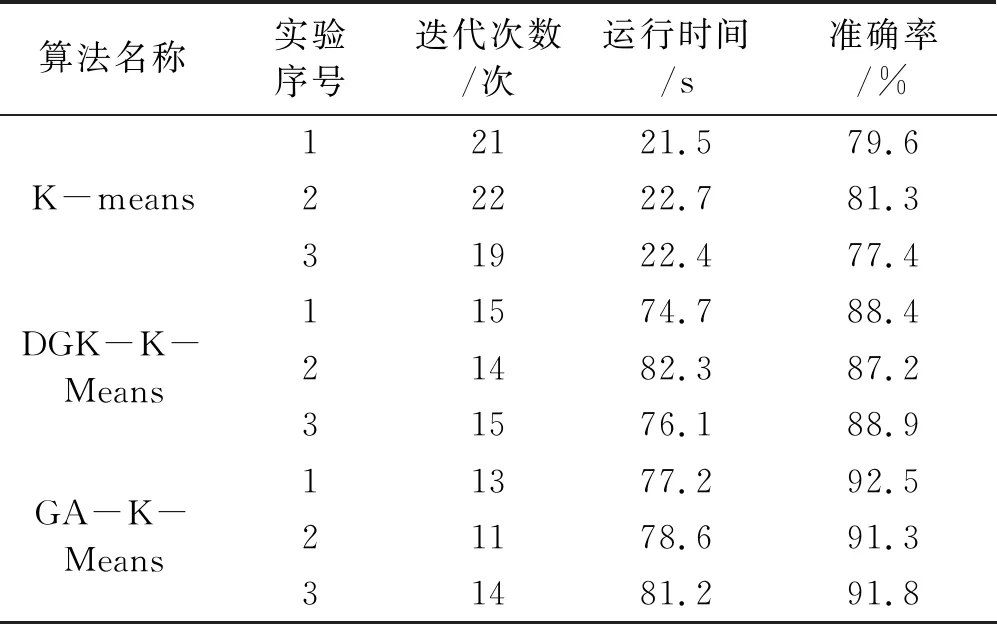
表2 试验结果对比
从表2可知,传统的K-means算法由于随机选取初始聚类质心导致分类准确率较低,而DGK-K-means算法与GA-K-means算法选取了较优的聚类质心,因此极大提高了准确率。同时由于初始聚类质心的选取比传统算法更合理,因此K-means迭代次数也随之减少。然而DGK-K-means算法和GA-K-means算法对于最优初始聚类质心的选取依赖额外的优化算法,且优化算法的计算量较大,平均运行时间更长。相比于传统K-means算法,GA-K-means保证了准确率和稳定性,且与DGK-K-means相比,通过遗传算法获取的初始聚类质心效果更优,能够获取更高的准确率。
为了客观评价上述3个算法的聚类效果,笔者采用轮廓系数、CH(calinski-harabaz)指标以及DB(davies-bouldin)指数作为聚类质量评价标准,3种指标都代表聚类结果簇的凝聚度,其中轮廓系数越接近1,表示聚类效果越好;CH指标越大,表示聚类效果越好;DB指数越小,表示聚类效果越好。聚类结果评价如表3所示。
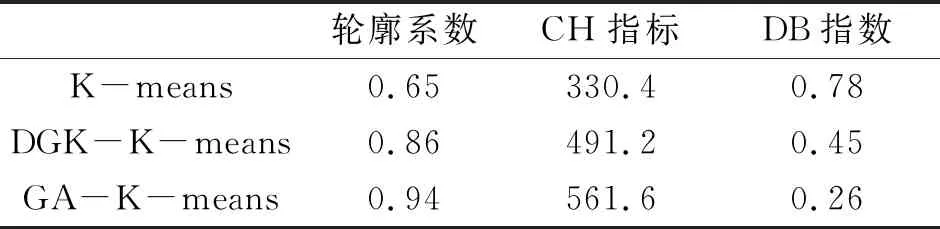
表3 聚类结果评价
从表3可知,GA-K-means算法的聚类效果要优于K-means算法和DGK-K-means算法。
3.2 并行化算法实验
并行化加速实验的软件环境为Hadoop平台,Hadoop集群中配置5台机器,其中一台为管理节点,4台为工作节点,所有节点都为腾讯云服务器,具体配置如表4所示。

表4 Hadoop集群配置表
并行式GA-K-means算法准确度测试仍然采用和串行算法一致的方法,每组试验运算3次,取3次的准确率均值作为衡量的标准,具体结果如表5所示。

表5 并行算法准确率测试
算法并行化对结果准确率并无影响,并行式GA-K-means算法在对数据进行加速的情况下,仍然能保证稳定的准确率。图8为并行化GA-K-means算法的集群加速比测试结果示意图。算法具体运行时间如表6所示。
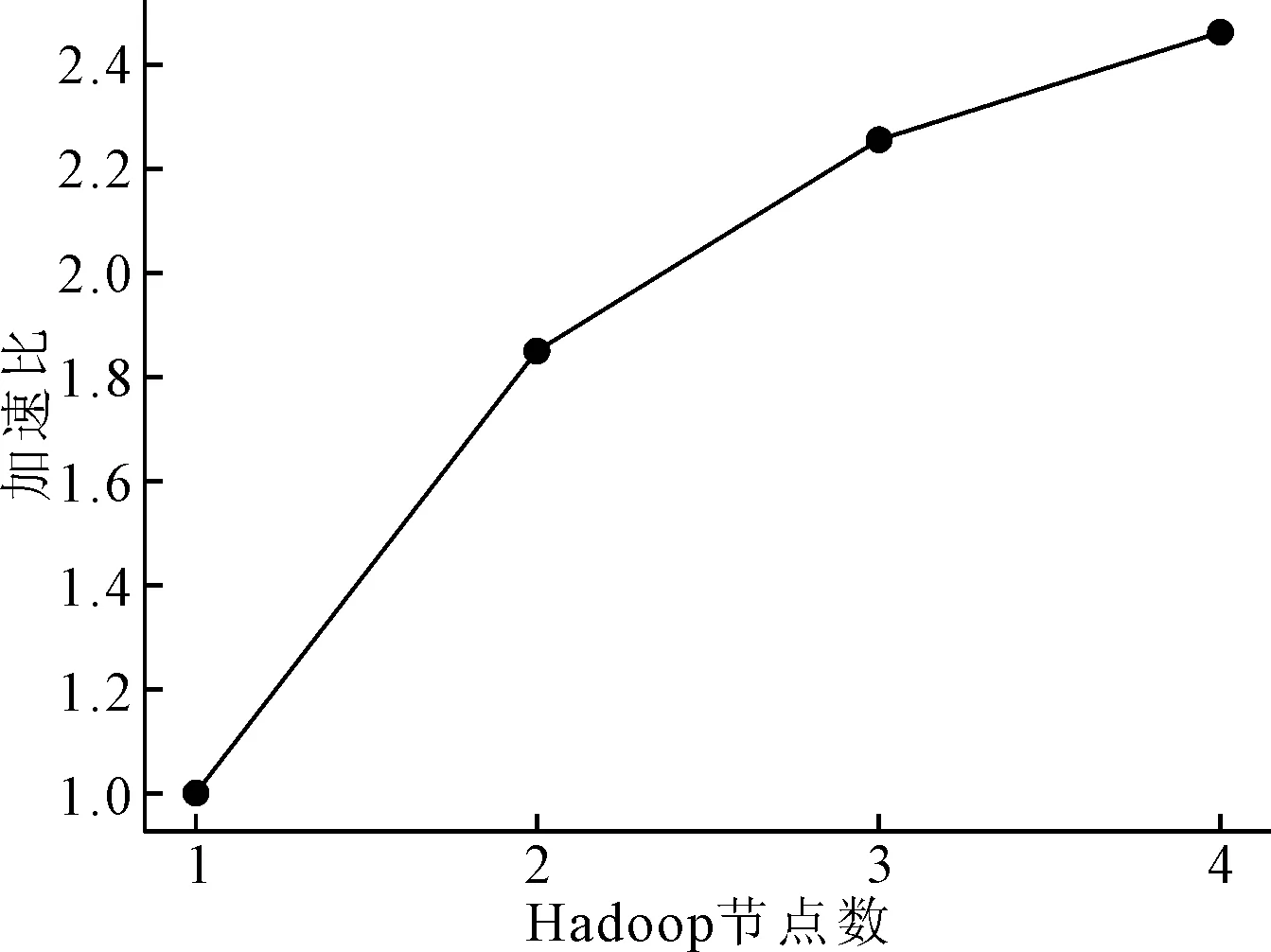
图8 节点加速比测试结果

表6 并行算法运行时间
随着Hadoop平台节点数的不断增加,算法的数据处理效率也不断上升,但是算法的加速增长率却逐渐下降,这是因为节点增加导致计算资源增加,Mapper任务与Reducer任务之间的通信复杂度升高,并且数据切片更加细化,加速效果逐渐减弱,因此算法性能增长速率逐渐下降。
4 结论
笔者基于高压输电线路合闸故障数据特点以及K-means算法对高压输电线路合闸故障展开研究。针对K-means算法的缺点进行改进,提出了基于遗传算法的K-means聚类算法,解决了初始聚类质心不稳定的问题,然后针对算法迭代次数过多、运行速度慢会影响实际工况数据处理效率问题,设计了两段式的并行化优化算法,提升运行效率。通过分析实验结果可知,所设计的并行式GA-K-means算法不仅弥补了传统K-means算法的不足,并且在保证算法运行效率的基础上,还能够将分类准确率稳定在91%。
