初中数学动点问题的教学策略研究

冯玲玉

【摘要】在初中数学的复习中，动点问题是重难点所在，同时也是中考的必考题型，而动点问题中的二次函数的应用为例，又是学校在初中数学复习中的主要难点，这就要求教师在平时教学中要采用合理的练习步骤和教学策略，以正确引导学生解题，进而发散学生的数学思维，从而提高思维能力，并改善教学方法.

【关键词】二次函数动点问题;教学策略

初中数学课程开始涉及函数，函数问题都是初中数学学习的重点和难点，尤其是二次函数更是中考压轴题当中的必考点，通常会以动点题的形式出现，而动点问题也是学生们学习数学的难点之一，根据学生们课堂的反馈以及做题情况来看，动点问题复杂而且难以理解.考察了学生对于基础知识的掌握情况以及深入探究知识的能力.所以对于二次函数动点问题的教学策略研究至关重要，那么我们就以二次函数为例展开研究.

1 初中数学二次函数动点问题的简述

二次函数动点问题被定义为：通过研究一个动点问题把函数的基本特性与几何图形有机组合，这就需要学习者对二次函数动点问题具有比较强的理解力，对学习者来说就具有一定挑战性，此外，学习者一旦能了解二次函数动点问题，综合运用理论知识的能力和解题的能力就会增强，因此研究问题也就会比较轻松.能够利用掌握的函数基础知识去解题，这不仅可以巩固学习知识点，还可以提高学生思考和解决实际问题的能力，从而传播学生的数学思想，教会学生将数与形、数学建模相结合，形成数学思维，解决实际问题[1].

2 解决数学动点问题的困难分析

2.1 学生在解决动点问题时的困难

初中数学动点问题涉及的知识具有很强的综合性，解决问题的要求比较高，导致很多学生在解题时遇到困难，不知从何入手.那么困难点体现在哪些方面呢？总结以下的几个方面：一是存在理解性困难.对于题目的关键信息和隐含条件，以及需要求的问题等内容很难理解，不能准确把握题中关键条件以及切入点，思路不清晰，题中的问题不能與所学知识联系起来，导致理解困难.第二，有选择性的困难.动点问题的求解方法具有很强的灵活性.许多学生不知道思考问题时应该选择哪些数学公式、定理和解决问题的方法，进而解题思路不清晰.第三，无法找到变量关系.二次函数关于动点问题的描述相对较长，一些学生遇到偏长的题目会有抵触心理，不会将文字信息转化为数学信息，建模能力较弱，不会提炼关键条件，问题中变量、不变量与实际条件之间的联系都不能发现，连函数关系也不能表示，使得难题不能准确地解决[2].

例1 如图1，抛物线y=ax2+bx+c经过A（0，4）、B（-2，0）、C（6，0），过点A作AD∥x轴交抛物线于点D，过点D作DE⊥x轴于点E，点M是四边形OADE的对角线的交点，点F在y轴负半轴上，且F（0，-2）.

（1）求抛物线所对应的函数关系式，并直接写出四边形OADE的形状;

（2）当点P、Q从点C、F同时出发，点以1m/s的速度沿CB、FA方向运动，移动时间为t秒，在运动过程中，以P、Q、O、M四点为顶点的四边形的面积为S，计算出S与t之间的函数关系式，并写出自变量的取值范围[3].

分析 （1）解题关键为将点代入解析式并求出二次函数关系式，再通过二次函数关系式性质判断图形，同时考察了四边形的判定定理.（2）解题关键在于找出题中全等三角形并运用三角形面积来解题，进而求出S与t之间的函数关系式.但许多学生求出二次函数关系式以后不能进行综合分析，不能将动点问题与全等三角形的判定有机结合，因而导致解题出现困难.

2.2 出现困难的原因分析

学生在解决动点问题时会出现困难，分析原因有以下两方面：

2.2.1 教师方面的原因

其一是教师教学态度的影响.动点问题对于学生来说确实是难题，偏题，有些教师在遇到此类问题时，不能做到耐心、细致、反复地为学生讲解;其二是教师教学方法的影响.部分教师在讲解此类问题的方式较为单一和固化，讲授课程机械化或者课堂枯燥乏味，不能将现代化的教学手段应用到教学当中，可以应用多媒体教学或者引入动态画板到教学当中，直观演示和讲解相结合，缺乏探索精神.所以，这就无法丰富学生的数学思想和开阔学生的眼界，也造成了学生思想的固化和解决问题的障碍;三是老师不能掌握学生求解难点的因素，就不能因材施教.如果教师不能掌握不同学生求解难度的因素，就无法解决学生的问题.

2.2.2 学生方面的原因

动点问题由于题型的复杂性和综合性强，对学生而言既是难题又是痛点，原因主要有以下三方面：首先，认识力不佳.初中阶段学生的抽象思维能力还处在上升的发展阶段，易受意志、心态、情感等非智力因素的影响以及对现有数学文化知识的限制，造成了学生对二次函数动点问题在具体解决方面的知识欠缺;其二，解题的思路并不清晰，思路也不够敏捷，所见问题较少，也没有解题的整体意识，面临各种类型问题也找不到解题的突破口，导致困难增加，进而失去了对动点问题的解题兴趣;其三，缺乏解题经验.部分学生对解决动点问题缺乏兴趣，解题的方法不够多样化，思维窄化，使学生从主观意识抵触动点问题，解题思路不清晰.

3 教学应对措施

3.1 解决动点问题的方法要多样化

教师在平时引导学生解决动点问题时，在已有教学方法的基础上，不断探究新的方法，引导学生一题多解，启发式教学，在解题的过程中注意将数形结合的思想方法渗透到教学中.有不同解题方法的同学，在课堂进行交流和分享，可以让学生掌握不同的解题方法，发散思维，这样既能拓宽学生的思维方式，又能帮助学生回顾之前的知识，并逐步形成综合运用知识的能力.

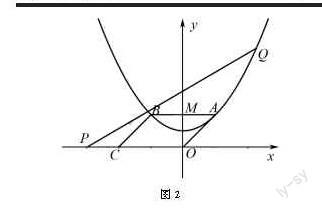
例如：在课堂讲解中，学生们遇到了一个测试问题（如图2）：二次函数的关系式是y=0.25x2+1，点C的坐标为（-4，0），平行四边形OABC的顶点A、B在抛物线上，AB与y轴交于点M，已知点Q（x，y）在抛物线上，点P（t，0）在x轴上.当四边形CMQP是一个以MQ、PC为腰的梯形时，找出t关于x的函数解析式和自变量x的取值范围.

这道题是典型的二次函数动点问题，由点的运动形成特殊图形，学生要理解题意，并且能够综合运用知识，梳理解题思路，找到恰当的解题方法，这道题有以下几种解题方法：（1）解析法，根据题干给出的二次函数关系式得出对称轴，进而求出点A与点M的坐标.接下来，连接CM并计算直线的CM解析式，并运用梯形上下底平行，获得t关于x的函数解析式;（2）三角函数法，构建直角三角形，并使用三角函数进一步求解直角三角形;（3）相似法，可以运用题中已知的相似三角形得到相似比，或者结合题干信息来构造相似三角形，进而求解.因此，教师要多引导学生将知识融合到一起，经常在头脑中形成知识网，善于挖掘多种方法解题.

3.2 与生活联系，用辅助工具解题

数学与我们的生活密不可分，学之用之，将数学与实际生活相联系，才能更加深入了解学习数学的意义，产生学习数学的浓厚兴趣，对于知识形成探究的精神，能够主动思考问题，可以利用数学思想和方法解题，例如：数形结合、类比、化归、数学建模等.而这些都需要教师日常教学的引导和示范.在教学中，教师通过讲解渗透数形结合和数学建模的思想和方法.例如，在寻找二次函数关系式时，绘制二次函数的图象并结合图象进行解释将更加直观.

3.3 引入多媒体、几何画板教学

二次函数动点问题难就难在综合性和点的“运动”，学生不能在头脑中形成运动轨迹，因此对于多种情况考虑得不充分，如果教师可以在课堂上可以运用现代化教学手段，例如：多媒体、动态几何画板等.讲解过程中，将直观的图形与讲解相结合，运用动态画板演示出点的运动轨迹，以及在运动中形成的图形，会让学生印象深刻，理解性更强.使用多媒体教学不仅能吸引学生的注意力，而且可以带着问题观察和思考，通过自身的观察得到答案，提升学生的学习数学的成就感，并理解形成过程，了解内涵，更好的应用. 运用这对学生将来解决二次函数的运动点问题有很大帮助，不再困难.

4 动点问题解题类型与教学要求

4.1 动点问题解题类型

二次函数动点问题可以分类解决，掌握问题的类型以后，可以帮助教师更有针对性地教学，有利于提高教学效率和改善教学效果.

4.1.1 根据问题分类

从问题出发进行分类，二次函数动点问题主要可以分为三种类型： 求最值问题，求函数表达式的问题，求动点的存在性问题.

4.1.2 根据动点的个数分类

从动点的个数来看，可以把二次函数动点问题分为两类：单动点问题和双动点问题.

4.1.3 根据函数与图形的结合分类

就函数和图形之间的结合问题来说，可以包括：函数与矩形和四边形结合，二次函数与直线结合问题，与椭圆結合问题，以及与三角形结合问题等等.

4.2 动点问题的教学要求

教师在提问时，对以下两个方面的教学要加强.

4.2.1 注重知识点间的衔接

由于在二次函数动点问题中，会涉及初中三年学习的知识点，因此要求学习者不仅仅需要掌握各知识点之间的联系，同时还要灵活运用，从而了解该问题中的变量与方程相关，从而为动点问题解决奠定良好的基础.

4.2.2 加强各问题之间的联系

动点问题通常至少由三个问题所构成，而各个问题间往往会产生递进关系，因而联系更加密切.比如，二次函数关系式就是后面求最值问题的基石，也可以为存在性问题做好了铺垫.因此学生在做题时如果可以了解问题之间的连接关系，并且能够恰当地运用，也就能够提高解动点问题的效果.

5 结语

二次函数动点问题是初中数学学习的重点和难点，也是学生在初中数学学习中的痛点，在教学过程中，教师要不断练习与探究此类问题，不断探究新的解题方法，做到一题多解，让学生在遇到此类问题时能够产生源源不断的解题思路，逐步消除学生的畏难心理，以积极的态度解决此类问题，提高综合运用知识的能力和解决问题的能力，形成数学的核心素质，并改善初中数学动点问题学习的现状.

参考文献：

[1]姚璐.基于问题解决的初中数学课堂教学设计——以“二次函数的应用”教学为例[J].数学教学通讯.2019（02）

[2]沈启芳.初中数学中动点问题的教学研究[J].新教育时代电子杂志，2019（36）：1.

[3]周航.初中数学动点问题的解题策略探讨[J].新课程（中学），2015（7）：102-103.