纸笔测试中空间观念的测评维度与试题设计

潘红娟

【摘 要】具备空间观念是小学生基本的数学能力，通过纸笔测试诊断小学生空间观念发展水平是当前评价研究的难点。本文基于空间观念的内涵与具体表现，对空间观念从“图形想象”“图形分析”“方位想象”“运动想象”四个维度，进行相应的能力分解与能力描述，并用具体试题加以解释与分析，为空间观念的评价研究提供实践案例。

【关键词】小学数学 纸笔测试 空间观念

具备空间观念是小学生基本的数学能力，课程标准中提出培养学生“具有初步的逻辑推理能力与空间观念”的要求。显然，发展学生的空间观念是小学数学教学的重要目标，其发展水平标志着学生数学能力水平的高低。

当前国內关于空间观念的研究，主要集中于基础研究与教学策略研究，如何通过纸笔测试来诊断小学生空间观念的发展特点，仍是小学数学教学与评价研究的难点与瓶颈。查阅相关文献，虽有一些零散的测评试题，但是较为全面反映空间观念表现的测评工具十分缺失。笔者尝试对空间观念进行细化分解，并用试题列举的方式加以解释，试图起到使能力维度与试题内容之间互为解释、互为支持的作用。

要谈空间观念测评，就有必要对空间观念进行相应的内涵界定。事实上，当前对空间观念并没有十分明晰、统一的概念界定。很多时候，我们很难将空间观念与空间能力、空间思维等概念区别开来。根据以往研究与课程标准的具体描述，我们对空间观念做如下定义：空间观念是以空间形式为主要对象，以空间知觉、表象为主要心理活动过程，在头脑中进行几何抽象、分析与综合（包括图形的分解与重组）、判断与推理（包括图形的运动及二维、三维间的转换）的思维能力。

本文无意于给出空间观念测评的严谨测试框架，仅是从教学与评价实践的需要出发，将空间观念分为“图形想象”“图形分析”“方位想象”“运动想象”四个维度，对这些能力进行相应的能力分解与描述，并提供相应的试题列举与分析，以期为后续空间观念的评价研究提供一些实践案例。

一、图形想象

空间想象是以空间知觉和空间表象作为基础的。而空间表象，是指在大量空间知觉的基础上，形成关于物体、图形的形状、大小以及相互位置关系的印象。空间想象则是在空间表象的基础上，经过加工、改造、结合，产生新表象的心理过程。

图形想象能力，指学生能否根据图形形状联想生活中的相关物体;能否根据数学语言的描述想象几何图形或图形之间的关系;能否想象从不同位置观察到的几何体的形状;能否根据不同位置看到的形状，想象出物体的形状;能否根据部分图形想象或推断整个图形;等等。

（一）实物形状与几何图形的互逆转换

关于实物形状与几何图形的转换，具体表现为三个方面：一是能够识别所学的几何形体;二是能根据图形的形状、大小，在头脑中形成具体表象，并由此联想到具体实物;三是能根据实物或实物图，联想到它的三视图、展开图，能想到它的面、棱、顶点等。

试题列举：图1是一个长方体物品的长、宽、高，请你根据具体数据估计这可能是一个（ ）。

试题考查学生“由几何体想象实物”的能力。需要学生根据图形名称及长、宽、高的实际长度，在头脑中形成关于形状、大小的表象，由此判断出这是一个类似于文具盒的实物。显然，试题的指向与空间观念的内涵十分契合。

（二）几何体与三视图的互逆转换

指向“几何体与三视图互逆转换”的命题：一方面，可以给出几何体，根据几何体判断或画出三视图，考查学生将“立体”转化为“平面”的能力;另一方面，可以设计“由不同方向的形状图”还原“几何体的形状”，考查学生由“平面”想象“立体”的能力。

试题列举：由一些同样大小的立方体搭成的几何体，图2是从上往下看到的形状，数字表示该位置立方体的个数。如果从右面看，则这个几何体可看到的是（ ）。

此题是对学生“几何体与三视图互逆转化”能力的综合考查。首先，需要学生根据左图中从上往下看到的形状与数量，在头脑中形成这个几何体的具体表象;其次，想象出这个立体图形从不同方向看到的平面形状。从这个意义上说，学生经历了“二维”与“三维”的两次转换，显然，空间观念考查便得到极好的体现。

试题列举：图3是一个长方体，其阴影部分的面积是多少平方厘米？

我们大多会将三视图与几何体的转换作为“不同方向观察物体”内容学习的专属，事实上，结合图形认识、图形测量等内容进行考查同样可为。此题便是将长方体知识融入空间观念测评的极好例子，用“求阴影部分面积”这一任务，来考查学生是否能想象出长方体每个面的形状与大小。所以，通过平面想象空间立体，是直观几何学习的重要内容与重要方式。

（三）几何体与展开图的互逆转换

“几何体与展开图的转换”同样是二维、三维间转化的重要视角。根据展开图或立体图，在头脑中经历“折”或“展”的过程，其中必然涉及关于“形状”、关于“位置”的表象建立。

试题列举：图4是一个长方体的展开图。

①长方体的棱长总和是（ ）cm。

②如果以A为底，请用字母“B”标出这个面的对面。

试题并不满足于“已知长、宽、高，求棱长和”的技能考查，题①需要学生将展开图还原成长方体，由此判断出长、宽、高，求得棱长总和;题②更是需要学生经历“折的过程”与“折的结果”想象，由此判断A为底面时相对面的形状与位置。

（四）图形拼组想象

根据语言提示，进行图形拼组的想象，同样是可以考查的维度之一。因为在拼组过程中，需要学生在头脑中进行几何分析、判断与推理。

试题列举：图5中五个图形都是由相同的小正方体搭成的。选择（ ）能搭成这个模型。

A. ① ②        B. ① ④         C. ② ④        D. ③ ④ ⑤

解答此题同样需要经历“空间知觉—空间表象—空间想象”的过程，五个图形怎样可以搭成长方体，需要对头脑中的表象进行加工与改造。通过尝试，学生将不同的组件拼组，想象出每一次拼组的过程、拼搭的位置，以及拼搭所形成的形状。

二、图形分析

（一）复杂图形的分解与重组

能在头脑中进行几何抽象、分析与综合、判断与推理，是重要的空间思维能力。因此，能从复杂的图形中分析出基本图形，能分析其中的基本元素及其关系，应该是空间观念测评的维度之一。

试题列举1：

图6中缺了（ ）块。

试题所涉及的基础知识不多，侧重于考查图形的分析能力。由空白部分与小长方形的大小关系，想象出缺了几块小长方形，显然，图形分解、估计、推理的能力蕴含其中。

试题列举2：如图7，每个小方格的边长为1cm，求△ABC的面积。

此题着眼于“多边形的面积”的知识内容，为平面图形的分析。

学生需要将三角形划归为若干个基本图形的“差”或若干个基本图形的“和”。这就需要学生在头脑中进行图形分析，可分解成“正方形-空白三角形”（如图8a），可分解成“三个三角形相加”（如图8b），或通过等积变形，转化为“已知底、高的三角形”（如图8c）。当然，除了这几种方法，图形分解、重组、转化的方法策略还有很多。同样，这需要空间观念的支持。

（二）以运动的眼光分析图形

让静态图形动起来，使图形在学生头脑中产生运动变化，使较复杂的图形变化成简单的图形，同样是空间观念考查的重要视角。

试题列举：如图9，每个方格边长是1cm，求图中阴影部分①②的面积和。

我们可以将图①向右平移，将两部分拼成一个长方形，求面积和。算式与结果：（                         ）;

我们也可以将图①或图②割补转化成梯形，求面積和。算式与结果：（                         ）。

这道题考查的意义在于将面积计算与图形运动有机结合，根据描述，将静态的图形动态化，头脑中进行平移运动或旋转运动，转化为长方形或梯形来解决。

上文中“求三角形面积”一题，将不规则三角形转化为已知底和高的三角形，同样是“运动思维”在空间图形问题解决中的极好运用。

三、方位想象

能想象出物体的方位与相互之间的位置关系，是空间观念中关于“方向与位置”内容的能力表现。具体表现为：能根据物体或图形相对于参照点的方向和距离确定其位置;能根据方位描述或运动路线，想象物体所在的位置;能想象物体运动的方向与路线;等等。

（一）方向的想象与描述

试题列举：选择“东、南、西、北”填空。

（1）傍晚放学，小远走出校门，迎面看到太阳，校门对着（ ）面;

（2）接着，小远坐公交车回家，他看到太阳在他的左边，公交车向（ ）方向开;

（3）到了十字路口，公交车右转弯，现在向（ ）方向开;

（4）此时，小远看到他右边是医院的大门，医院大门对着（ ）方。

显然，这道试题凸显了“方位想象”的鲜明特征，需要学生置身于真实的空间中，进行方位想象，并推理判断出运动的方向以及物体相对于参照物的方向。

（二）位置的想象与描述

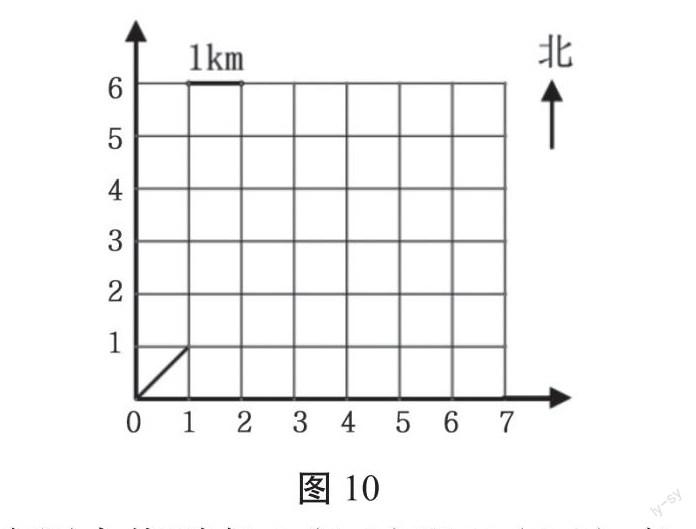
试题列举：图10中，小方格的边长是1千米，小方格对角线的长度是m千米。

（1）在图中找到点A（5，2）和B（2，5），点A在点B的（ ）偏（ ）（ ）度方向，距离是（ ）千米。

（2）若过A、B两点画一条直线，则从A点出发沿此直线去B点，是向（ ）偏（ ）（ ）度。

此题融合了三个方面的能力考查：“根据方位描述找到物体的位置”“根据位置用方向与距离进行描述”“能想象并描述物体运动的路线”。尤其是A点与B点的位置关系、A点到B点的运动路线，无论是方向、角度还是距离，不仅需要空间观念支持，同时需要逻辑推理。因此，本题是一道融合了“数对”“极坐标”等多个“位置”相关知识，融入了空间观念与推理能力等多项能力考查的综合试题。

四、运动想象

相较于其他维度，“运动想象”与空间观念水平联系更为紧密。为了将基于图形几何领域中所要学习的“运动变换”内容与其他运动区别开来，我们简单地将其分为“图形变换想象”与“一般运动想象”。图形变换想象，仅指向于“全等变换”和“相似变换”。其中，全等变换包括平移、旋转、对称，相似变换指向于“图形的放大与缩小”。

（一）运动变换想象

要考查学生关于“运动变换”的想象能力，以对称、平移、旋转等相关内容作为载体进行命题，便是可行的方式。

试题列举：如图11，将一张正方形纸片对折，再对折，剪去三角形，得到五边形AMNCD，将折叠的五边形展开后的图形是（ ）。

本题是对“对称变换”的考查，试题并不是简单的图形再现，而是要求学生基于“对称”的概念理解，想象对称变换的过程，分别形成正方形对折后的图形表象和图形展开后的形状表象。

试题列举：如图12，一个小圆沿着一个等边三角形滚动一周，若小圆半径是2cm，三角形边长是10cm，那么，小圆圆心滚动一周留下的轨迹是（ ）cm。

本试题如果从知识技能维度考虑，是考查“圆周长”的试题，但同时又很好地将“平移运动”与“旋转运动”有机综合，学生在头脑中形成运动的表象，从而推理出小圆圆心滚动一周的轨迹。

（二）一般运动想象

这里所指的一般运动，是指区别于小学阶段“图形变换”学习内容的其他运动情况。

试题列举：如图13，长方形ABCD的长为6cm，宽为2cm，E为AD的中点，如果将长方形ABCD绕轴L旋转一周，那么三角形EBC阴影部分扫过的立体图形的体积是多少立方厘米？

这道题的经典意义在于融入了空间观念中“图形运动想象”与“图形分析分解”两个方面的能力。不仅需要由平面运动想象出立体图形，同时需要对运动后形成的组合形体进行分解，并分析其底面半径、高等要素与平面图形中长方形长、宽之间的关系。

试题列举：如图14，院子的两堵墙分别为5m和8m，墙外是一片草地，墙上拴着一只小羊，绳长4米。如果将小羊A和小羊B分别拴在图14a、图14b中的位置，哪只小羊能吃到草的面积更大一些？相差多少？请用算式或其他方法说明。（结果可用含有π的式子表示）

试题虽蕴含了“旋转”运动，但因考查重心并不落脚于“旋转”运动的要素，因此，将其纳入“一般运动想象”的范畴。本题并不仅仅依赖于公式的运用，还需要想象出小羊运动的范围，并能分析运动后形成的半圆、四分之一圆的要素，以及其圆心的位置与半径的长度。从这个角度说，此题应该是考查运动想象的好题。

最后，值得说明的是，因测试材料本身所具有的综合性特征，每一道试题与能力维度间会存在并非完全一一对应的关系，可能某些测试材料会涉及多个维度，本文只是从能力侧重的角度进行相应归类。笔者以为，试题的分类并不重要，如何设计指向空间观念考查的好题才是重要的。