图说数学单元教学
2022-05-30刘祖希

【摘 要】 借助图形讲解数学单元教学的几个基本问题:单元教学的地位与价值、单元的分类、单元教学的设计流程、单元教学的实施流程,帮助读者直观理解数学单元教学的研究成果与操作方法,减轻理论学习负担,有效开展教学实践,辩证分析教育热潮.
【关键词】 图说;单元教学;价值;流程;辩证分析
近几十年来,教育领域的新理论、新概念、新热点层出不穷,往往来得快、去得也快,一线教师普遍反映“苦理论久矣”.以数学教育领域为例,就有20世纪80年代的“问题解决”,20世纪90年代的“建构主义”、21世纪初的PCK(教学内容知识)和MKT(面向教学的数学知识)理论,以及近几年的“核心素养”[1-3]“单元教学”“深度学习”“项目化学习”,等等.当前,我们又迎来了“作业设计”“跨学科教学”的热潮.
这一轮“单元教学”热潮有五六年了,目前已取得单元教学四个层面的研究成果.一是学理层面,包括单元教学设计的依据与策略、单元教学设计的价值指向、单元教学设计的路径,等等.二是概念层面,何为单元?何为单元知识结构?何为单元教学?等等,以及单元教学的等价概念,如主题教学、整体教学、结构化教学、大概念教学、大观念教学等.三是设计层面,包括单元教学的结构、设计流程等.四是应用层面,主要是针对中小学具体的教学内容来论述单元教学的设计与操作[4].鉴于中学教师教学任务繁重,难以系统学习这些理论研究成果,本文摘其精要、借助图形进行介绍,正如本文标题所言:图说数学单元教学.1 单元教学的地位与价值
单元教学并非全新的教学法,20世纪80年代它已广泛出现在我国中小学各学科的课堂之上[5-7].最新颁布的2022年版义务教育数学课程标准指出,当前推进单元整体教学设计,目的是要改变过于注重以课时为单位的教学设计,体现数学知识之间的内在逻辑关系,以及学习内容与核心素养表现的关联[8].也有研究者认为,现在又重视单元教学的理由是为了深化以单元教学为载体的学科教学,希望将其上升到学科教研的统领地位,而不仅仅作为课堂教学的方法和手段[9].
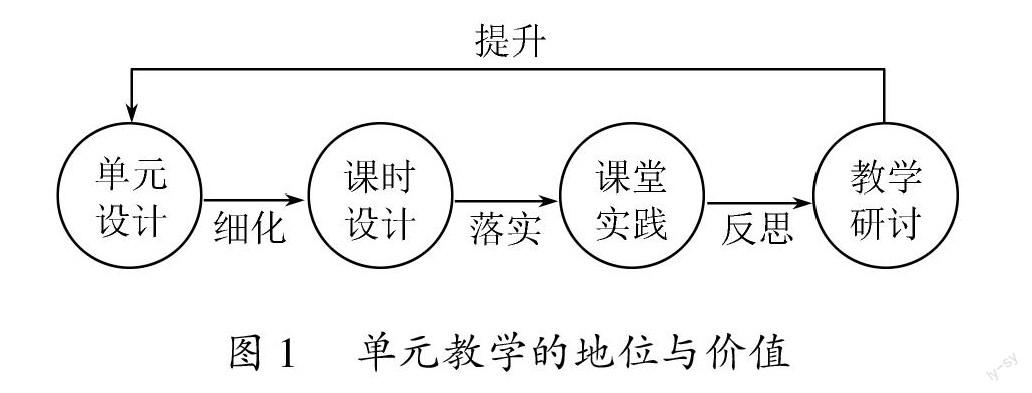
单元教学是相对课时教学而言的,无论把单元教学的价值拔得多高,它都不可能也不应该取代课时教学.事实上,单元教学更多的是一种教学观念与认识,实际操作只能以课时教学的形式出现.下面的图1反映了单元教学、课时教学在教学链条(包括课前、课中、课后)中的位置与关系[10].
单元教学的地位与价值
表明,单元教学设计对课时教学设计有指导、统摄作用,但需细化、分解为若干课时教学设计,从而付诸课堂实践;课后应开展教师个人教学反思,必要时开展集体教学研讨,从而提升认识,改进课前的单元教学设计.这是一个良性循环,体现了单元教学的地位与价值.理解了这一点,可以避免对单元教学产生盲从心理或抵触情绪.
2 单元的分类
确定学习单元,是开展单元教学的前提.单元,本意是指样本中自为一体或自成系统的独立成分.單元不可再分,否则就改变了事物的性质.单元是一个相对概念,比如相对于“课时”,“节”是一个单元;相对于“节”,“章”是一个单元;相对于“章”,整本教材也是一个单元.甚至还有跨章节、贯通整个学段的所谓大单元(或主题),比如“数的运算”就可以看作横跨中小学数学的一个大单元(或主题).2022年版义务教育数学课程标准正是将四个学段(第一学段“1~2年级”、第二学段“3~4年级”、第三学段“5~6年级”、第四学段“7~9年级”)、四个学习领域(“数与代数”“图形与几何”“统计与概率”“综合与实践”)的数学课程内容划分为若干个主题,便于分析“主题—单元—课时”的数学知识与核心素养的表现,适时开展单元整体教学[8].
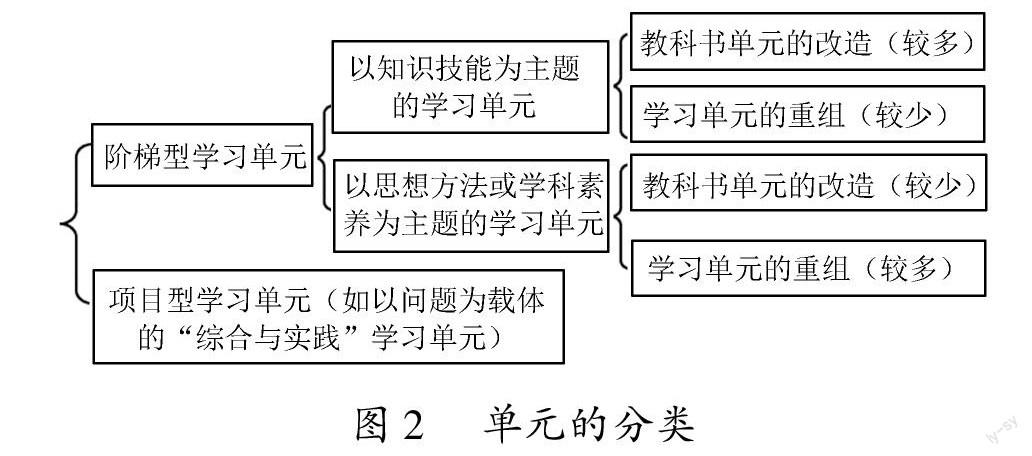
有研究者借鉴课程的分类法(阶梯型课程、项目型课程),将学习单元分为阶梯型、项目型(问题解决型)两大类,并将阶梯型划分为知识技能类、思想方法类,如图2所示[11].这种分类契合了数学课程标准所提出的数学“四基”:基础知识、基本技能、基本思想方法、基本活动经验.
单元的分类
还显示,知识技能类的学习单元可以较多地依据教科书的章节自然划分成单元,而思想方法类的学习单元则需要教师较多地进行跨章节的创造性重组.前者好理解(一般教科书已划分好单元),关于后者,我们举两个初高中的例子.
比如,有的初中数学教材(如苏科版)在不同年级不同分册安排了多次有关“反证法”的拓展阅读材料,可将它们组合成一个学习单元.
再比如,可用转化与化归的思想方法将高中范围所有关于“距离”的知识重组成一个单元(归结为探究“两点距离的最小值”),包括点到直线的距离、两条平行线之间的距离、异面直线之间的距离、点到平面的距离、直线到平面的距离、平面到平面的距离,甚至集合与集合的“距离”.
进行单元教学设计之前,我们要明确学习单元是什么,哪些内容可以构成学习单元,以及为何要选取这样的单元.
3 单元教学的设计流程
确定学习单元后,怎样进行单元教学设计呢?2017年版高中数学课程标准指出,一般来说,单元教学设计大致分为三个阶段和五个环节(如图3).三个阶段是指前期准备、开发设计、评价修改.五个环节是指确定单元内容、分析教学要素、编制单元教学目标、设计单元教学流程、评价反思及修改.
其中,“分析教学要素”环节是单元教学设计前期准备阶段的重点环节,也是“编制单元教学目标”环节的前提.它又包括六个方面:教学内容分析、课程标准分析、学情分析、教材分析、重难点分析、教学方式分析[12].
不难看出,单元教学的设计流程与课时教学基本相同,并没有实质性地增加教师的负担.
单元教学设计的流程
还有研究者给出了基于问题驱动的中学数学单元整体教学设计模式(图4):研究者认为适当的问题与情境是实现数学单元整体教学设计的重要支点,以数学单元为主体的整体教学设计需重视问题驱动课堂的教学方式,整体教学观与问题驱动理论是指导数学单元教学设计的重要理论依据.教师只有围绕数学史、数学教材内容、教学目标、学生的数学现实四个方面整体理解单元内容,才能真正实现中学数学单元的整体教学设计,做到以问题驱动教学[13].
这一模式与2017年版高中数学课程标准给出的单元教学设计模式并不矛盾,只是更加突出数学的学科特点——在解决问题的过程中发展.
4 单元教学的实施流程
不同类型的学习单元所对应的单元教学流程有较大差异,因此有必要专门讲讲前述三种类型学习单元各自的单元教学实施流程.4.1 知识技能类单元教学
知识技能,即人们常说的“双基”:基础知识、基本技能.数学知识技能的教学以数学概念的教学最为常见.不难理解,值得开展单元教学的数学概念,往往是数学中的核心概念(也有人称为大概念、大观念),比如初高中的“代数式”“方程”“不等式”“函数”“导数”“三角形”“四边形”“直线与平面的位置关系”“圆锥曲线”等.
关于核心概念的单元教学流程,可概括为图5[4].具体来说,首先要给出核心概念生成的概念图(也就是它的下位概念),比如中学范围内“函数”可以生成“正比例函数”“反比例函数”“一次函数”“二次函数”“幂函数”“指数函数”“对数函数”“三角函数”“反三角函数”,以及“图象”“单调性”“最值”“奇偶性”“周期性”“导数”“极值”等下位概念,共同构成函数的概念图.
核心概念类单元教学的流程
然后将这些概念图划分为不同的路径,并分别开展相应的性质研究、应用研究等.比如,可选取“正比例函数”为路径1,研究正比例函数的图象、性质、实际应用等,并开展相应的练习与小结.可选取“一次函数”为路径3,同样研究一次函数的图象、性质、实际应用等,并开展相应的练习与小结.其他路径依此类推.
而且要注意,不同的路径之间可以关联起来,比如路径1“正比例函数”可与路径3“一次函数”关联,合并成一个新的大单元开展后续性质研究、应用研究、练习与小结.4.2 思想方法类单元教学
重视数学思想方法的教学是我国数学教育的特色与传统.数学思想方法既可以在数学知识技能的教学中进行渗透,也可以通过专题式教学进行系统学习. 思想方法类单元教学,其一般流程如图6所示[4].
图6 思想方法类单元教学的流程
首先要确定数学思想方法.数学思想方法本身也是极为系统的一门学科,其层次各异、种类繁多.教师要结合具体的数学知识技能、待解决的大量数学问题、精选相应的数学思想方法,因为数学思想方法不可能脱离知识技能而单独存在,它的适用对象也不可能只是少数问题(否则就不称其为思想、方法了).根据广大教师经验,中学数学最常见的思想方法类单元教学包括分类讨论、数形结合、函数与方程、转化与化归等.
然后围绕确定的数学思想方法设计或配置相应的题组(或称问题串、问题链),开展变式教学.要注意题组的典型性与层次性,既要以一当十又要拉开梯度,防止题海战术与机械重复训练.
接下来是师生共同解决问题的环节.与其他数学课相比,思想方法類单元教学的这一环节有其独特优势,因为解决问题的“金钥匙”已经明确了,就是所讲的数学思想方法;解决问题的“脚手架”已经搭好了,就是所选的题组(问题串、问题链).因此,这一环节可以充分发挥学生的主体性,教师作适当引导与点拨,让学生充分感受“势如破竹”“攻城夺地”的学习成就,感悟数学思想方法的威力与魅力.
最后的回顾总结环节必不可少,教师要引导学生领悟数学思想方法是数学发展和数学问题解决的根本力量,获得对数学思想方法的整体理解,既包括其普适性,也包括其局限性(没有万能的思想、方法).4.3 问题解决类单元教学问题是数学的心脏,数学无时无刻不是在解决问题中前进.数学教学亦如此,数学教材依靠问题情境、例题和习题来演进,数学试卷通过试题来串联.但这些问题大都是经过加工、简化而来的,有比较明确的解决方法(模式)和答案.事实上,仍有许多问题没有固定的解决方法和答案,需要教师引导学生自主探索,往往耗时较长,所需知识、方法、工具(如信息技术)超过学生当前认知水平甚至会跨学科.我们将这样的问题称之为综合与实践、数学建模、数学探究活动等,它们是积累数学活动经验的重要载体[14] .
可以针对这些问题的解决开展单元教学,图7就是问题解决类单元教学的操作流程[4].虽然其基本过程一目了然,就是提出问题、解决问题、单元总结,但我们可以从中看到许多其他数学课所没有的环节,比如需将初始问题分解为若干个新问题,并需要学生学习若干相应的新知识,以便解决这些新问题.这些新知识在总结环节被统称为“单元外已学知识”,纳入本单元知识体系后,新旧知识融为一体,形成结构化的新知识体系.
问题解决类单元教学的流程
5 单元教学的辩证分析
关于单元教学的研究成果与实践经验固然可喜,但也出现了很多认识误区.实施数学单元教学法,需注意以下辩证关系.
(1)防止单元概念的泛化,避免将非主干的知识技能、解题技巧当作学习单元,过度总结解题模型、二级结论(尤其是初高中毕业班).
(2)防止单元教学概念的泛化,避免将单元教学与传统的单元教材分析、单元复习混为一谈,本末倒置.
(3)单元教学目标与课程目标、课时目标三者之间是中观、宏观、微观的辩证关系.单元教学要与课时教学结合使用,两者互为补充、相辅相成、不可偏废,不可一窝蜂地炮制单元教学设计.
(4)单元教学除了教学内容的结构化、教学形式的结构化,更需要学生思维的结构化.要避免单元教学流于形式化,因为学生思维的结构化才是单元教学的精髓[15].还要避免单元教学内容结构化之后过于抽象,脱离社会,脱离学生实际.至此,本文完成了“图说数学单元教学”的任务,为笔者的“图说数学教育原理”文章系列 [3,9,16-18]增添了一个新的成员.让我们共同努力,把数学教育理论变得更加直观形象,把数学教育研究变得更加平易近人.
参考文献
[1] 刘祖希.我国数学核心素养研究进展:从数学素养到数学核心词再到数学核心素养[J].中小学教材教学,2016(07):35-40.
[2] 刘祖希.访史宁中教授:谈数学基本思想、数学核心素养等问题[J].数学通报,2017(05):1-5.
[3] 刘祖希.图说数学核心素养[J].中小学课堂教学研究,2020(10):59-62.
[4] 喻平.数学单元结构教学的四种模式[J].数学通报,2020(05):1-8.
[5] 张维忠,孙名符.用整体原理探讨数学课堂结构[J].西北师范学院学报(自然科学版),1988(03):85-90.
[6] 涂荣豹,宁连华.中学数学经典教学方法[M].福州:福建教育出版社,2011:303-315.
[7] 吕世虎,杨婷,吴振英.数学单元教学设计的内涵、特征以及基本操作步骤[J].当代教育与文化,2016(04):41-46.
[8] 中国人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022:86.
[9] 刘祖希.图说五种常用的数学教学法[J].中小学课堂教学研究,2020(05):56-59.
[10] 朱瑜.单元教学视野下回应式课堂的研究与实践[M].上海:华东师范大学出版社,2018.
[11] 章飞,顾继玲.单元教学的核心思想与基本路径[J].数学通报,2019(10):23-28.
[12] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:171-174.
[13] 王海青,吴有昌.基于数学单元的整体教学探索与实践:问题驱动的视角[J].数学通报,2022(03):27-32.
[14] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:47.
[15] 喻平.小学数学隐性课程资源分析[J].小学教学(下半月·数学),2021(07/08):22-27.
[16] 劉祖希.图说数学教育理论模型的建构[J].中小学课堂教学研究,2021(05):60-64.
[17] 刘祖希.图说数学教育研究方法[J].中小学课堂教学研究,2022(04):65-68.
[18] 刘祖希.图说数学教育理论的融通[J].中学数学杂志,2022(02):6-10.
