数学文化在我国高中数学教科书中的呈现

2022-05-30邵诺愉张维忠

中学数学杂志(高中版) 2022年4期

邵诺愉张维忠

【摘要】数学文化融入数学教学是发展学生核心素养的重要实现路径之一.借鉴相关理论，基于内容条目、融入方式和认知水平3个维度构建分析框架，分析讨论了2019年人教A版高中数学必修教材中数学文化的呈现情况.结果表明：新教材必修部分数学文化内容丰富，但不同主线下分布不均衡;数学与生活、科技的文化融合程度高，但与数学史的融合程度低.建议教材关注数学建模、数学探究活动与数学文化的整合，均衡数学文化分布，提供丰富、多样的情境，变更设问角度，深化数学史融合程度;建议教师重视旁注式数学文化内容的呈现，探究多样的数学文化融入数学教学的实践路径，避免数学文化的工具主义倾向.

【关键词】数学文化;教科书;高中

数学教科书是落实数学课程标准，传递数学学科内容，指导教师数学教学，引领学生数学学习的重要工具，同时也是渗透优秀数学文化的重要载体[1].进入21世纪以来，数学文化在课程标准中的地位不断凸显，《义务教育数学课程标准（2022年版）》充分肯定了数学文化的价值，并在教材编写建议中提出“在教材中介绍数学文化，為教材使用者提供广泛的素材资源和开放使用空间”[2].伴随着数学教科书的重编与更新，数学文化融入数学教科书成为数学教育研究的热点话题.数学教学必须从激发学生对这门学科的兴趣开始，而激发人们对数学的兴趣，本质上比激发人们对历史或文学的兴趣要困难得多.这是因为数学都是抽象的，它在人类思维中所起的作用并不是先天清晰的，而每个学生都知道历史是什么，为什么他应该学习历史，以及他可能从历史中获得什么[3].可见，数学文化融入数学教科书不仅是课程标准的基本要求，也是激发学生学习兴趣及培养其科学精神的应然向度[4].然而研究表明，数学文化在中学数学教学中并没有落到实处，存在“高评价、低应用”的问题.研究数学教科书中的数学文化，能够帮助数学教学工作者更好地基于教材进行教学设计，让学生更容易接受数学知识的发生、发展和应用过程，发展学生的核心素养，同时也能发现当下教材对数学文化呈现的不足.本研究选取我国目前正在使用的高中数学教科书作为研究对象，借鉴前人的相关研究构建理论框架，分析教科书中呈现的数学文化，以期为数学教师教学及教材修订提供启示与借鉴.1 研究对象与分析框架

1.1 研究对象选取人民教育出版社2019年出版的《普通高中教科书·数学》必修[5]（2册）（以下简称“新教材”）作为研究对象.人教版教科书是基于2017年颁布的国家《普通高中数学课程标准》编写的，是一套具有代表性的教科书，能够体现我国最新的课程理念与实践探索.从内容上将其划分为预备知识、函数、几何与代数、概率与统计、数学建模与数学探究活动这5大主线.

1.2 分析框架

关于数学文化的内涵，不同的学者有不同的观点.美国著名数学家怀尔德将文化定义为“习惯、仪式、信仰、工具、风俗”等由一群人所共有的所谓“文化流”之集合，并认为数学应该被看作是文化的一个分支[6]. 黄秦安[7]、张定强[8]等人从数学学科角度定义数学文化，认为数学是一种思想方法、一种具有审美特征的艺术，数学文化具有比数学知识体系更为丰富和深邃的内涵，是对数学知识、技能、能力和素质等概念的高度概括.《普通高中数学课程标准（2017年版2020年修订）》[9]（下简称“新课标”）则指出，数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展，还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动.

在对数学文化的概念界定和前人研究的基础上，围绕“呈现内容”“呈现方式”“呈现水平”这3个角度，选取数学文化内容条目、融入方式和认知水平3个维度构建分析框架.基于对数学文化的广义理解，借鉴王建磐[10]等人的研究，将数学文化的内容条目分为数学史、数学与现实生活、数学与科学技术和数学与人文艺术4类;基于“显性化”和“多样化”原则，借鉴王嵘[4]的研究，将数学文化的融入方式分为片段式、旁注式、问题式、短文式和图表式五类;借鉴Stein[11]等人对数学任务的分类，将教科书中数学文化的认知水平分为了解性、无联系程序性和联系程序性3类.

其中内容分布和5大主线进行交叉分析，以探究数学文化在不同主线下的呈现特征;认知水平和内容分布进行交叉分析，以探究教材对不同内容的数学文化的认知要求.2 新教材必修中数学文化的呈现

2.1 内容分布

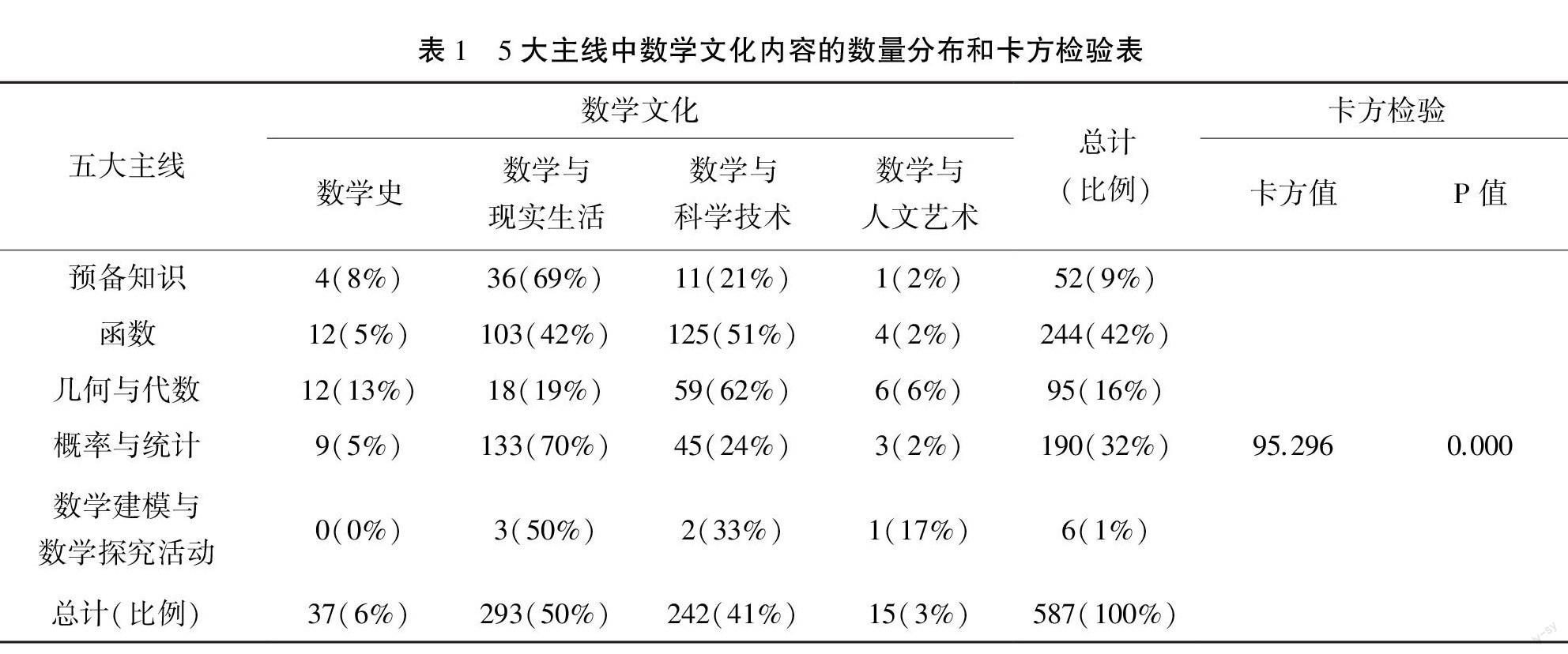
经统计（表1），新教材必修部分总共融入了数学文化587处.从总量上看，数学与现实生活类占比一半，共293处，数学与科学技术类次之，共242处，数学史和数学与人文艺术类相对较少，分别占比6%和3%.说明新教材突出了数学与现实生活和科学技术领域的密切关系，旨在向学生传达“数学源于生活，数学引领科技”的理念.

从卡方检验P值（P=0.000<0.05）可知（表1），5大主线中的数学文化类型分布有显著性差异.分析具体数据可知，在几何与代数主线，数学与科学技术类占比远高于其他三类，这是因为该主线中的平面向量部分采用了大量物理学知识.如，教材在介绍“向量的概念”时，类比数量的抽象过程，从力、位移、速度等物理概念中抽象出向量的概念. 在历史上，向量最初应用于物理学，被称为矢量.教材遵循了向量的产生背景，引导学生从物理学的角度理解向量，使得向量不再是一条抽象的有向线段.在概率与统计主线，数学与现实生活类占比最大，“统计”章节中呈现了许多与现实生活相关的统计数据，结合现实生活情境让学生体会数据统计的意义.例如，教材提供100户居民用户的月均用水量数据，来探究全体居民用户的用水情况，以培养学生形成“用样本估计总体”的统计思想.函数主线所包含的数学文化数目是5大主线中最多的，其中数学与现实生活、科学技术的融合较均衡，可见函数是综合性较强的主线，在高中数学中具有重要地位.

相比之下，数学史、数学与人文艺术类在5大主线中的占比都很少.这两类数学文化大多以阅读栏目、图片的形式呈现在教科书中，如函数主线下的“阅读与思考”栏目简单展现了函数概念经历了“变量依赖说、变量对应说、集合对应说”的发展历程，以数学史为载体，让学生感受随着研究深入，函数概念不断得到严谨化、精确化的表达，体验一把数学家的思维.引入良渚遗址人文背景，展现数学知识在遗址年代测定中的妙用，感受数学与人文交融的魅力.

2.2 融入方式

经统计，问题式数学文化主要以栏目问题、例题或习题的形式呈现在教科书中，在新教材必修部分中占比最大（65%），共计383处.其中包含了大量与现实生活和科学技术相关的情境.例如，教材中呈现了一则“依法纳税”的例题，要求学生根据表格数据和个税税额的计算公式求个税税额的函数表达式并绘制函数图象，要求学生在充分理解情境的基础上，结合应纳税所得额的计算公式，计算个税税额值.此类的文化情境能够让学生在解题的同时，形成良好的道德法制观念.图表式数学文化主要以图片、表格的形式呈现，包含了數学家肖像、数学标志、建筑、设计规划、日常生活、物理实验数据记录等内容，共计93处（16%）.片段式数学文化主要分布在新知引入环节和课堂探究环节，以知识讲解的形式呈现，共计57处（10%）.例如，教材通过列举抛掷硬币观察正反面、随机选取10位学生观察近视人数、随机抽取一支灯管测试其寿命、记录某地区7月份的降雨量等例子，归纳出“随机试验”的概念为：对随机现象的实现和对它的观察.这就是一个片段式数学文化的呈现.短文式数学文化以章前言、拓展栏目或主题学习的形式呈现，主要包括数学家生平介绍、数学家与数学知识、数学知识发展史、人文背景、学科起源与学科交叉等内容，共计29处（5%）.

另外，旁注式的数学文化虽然占比是最少的，但其内容十分丰富.仅25处（4%）旁注式数学文化就涵盖了所有类型的数学文化内容.旁注中的数学文化极大地丰富了学生的知识面，如学习复数时基于数学史向学生解释i的由来，迅速地拉近了学生与数学家的距离，使得i不再只是一个抽象的虚数单位;赋予card、log等数学符号以文学背景，解释其全称，感受数学符号并不是凭空捏造的，其背后都有文学含义.除此之外，还有经济类、物理类等丰富的跨学科文化也在旁注中有所体现.

2.3 认知水平

经统计（表2），联系程序性数学文化占比最大，共计364处（62%），无联系程序性数学文化共计123处（21%），了解性数学文化共计100处（17%）.从整体上分析，新教材必修部分对数学文化的认知水平要求较高，半数以上数学文化需要学生付出认知努力加以理解.

从卡方检验P值（P=0.000<0.05）可知（表2），新教材中不同的数学文化内容的认知水平有显著性差异.分析具体数据可知，教材对数学与现实生活、数学与科学技术类的认知水平要求较高，其联系程序性数量分别占了该类总量的71%和62%.另外，教材对数学史的认知水平要求较低，37处数学史中仅2处为联系程序性，33处为了解性，可见该版教材对多数数学史料的要求仅停留大致、笼统的认识，这就可能导致教师在教学过程中容易忽视对数学史的运用.

3 对数学教材修订及数学教师教学的启示

3.1 均衡数学文化内容分布，展现数学真正文化要义

在统计过程中发现，数学文化的分布存在不均衡的现象.一方面体现在不同主线下数学文化数目分布不均衡.《新课标》将数学建模和数学探究活动这一主线列为学生形成和发展数学学科核心素养的有效载体.而统计显示该主线的数学探究活动仅对纯数学问题展开探究，数学文化内容并不丰富.数学与物理、化学、生物、信息技术等学科有千丝万缕的联系，在社会、人文、艺术等领域的运用也愈加广泛，各学科的定量研究都离不开数学.概率与生物遗传、物理学中重心的变化规律探索、信息技术中的算法、社会学中的调查研究、文学作品重复率研究都可作为数学建模或数学探究活动[12]. 因此教材修订应多关注此类活动与数学文化的整合.

另一方面体现在同一主线下的数学文化内容相似程度过高，下面是几何与代数主线的3处问题式数学文化案例：

长江两岸之间没有大桥的地方，常常通过轮渡进行运输.一艘船从长江南岸A地出发，垂直于对岸航行，航行速度的大小为15 km/h，同时江水的速度为向东6 km/h.求船实际航行的速度的大小与方向.

有一条东西向的小河，一艘小船从河南岸的渡口出发渡河.小船航行速度大小为15 km/h，方向为北偏西30°，河水的速度为向东7.5 km/h，求小船实际航行速度的大小与方向.

一艘船垂直于对岸航行，航行速度的大小为16 km/h，同时河水流速的大小为4 km/h，求船实际航行的速度的大小与方向.

这3处数学文化分别设置在必修第二册6.2节的例题、练习和复习巩固中，相似情境设计固然有利于学生巩固知识，但这也易使数学文化的运用流于形式，且不利于学生创新思维的发展.同样的问题出现在预备知识中，学习“不等式”知识点时采用了多处类似“篱笆围菜园”的情境.对此教材修订建议同一主线下提供更丰富、多样的文化情境，同一文化情境也可以采取不同的设问方式.

如新北师大版高中数学教材对“平面向量运算”这一内容也给出了两个类似“小船过江”的情境，虽然在文化背景上具有重复性，但第二个情境新增了“要使小汽艇沿垂直河岸的方向到达对岸码头，船头方向又应怎样”的问题，促使学生从不同角度思考同一文化背景下的问题，可见数学最内在的文化特性应是数学本身，数学真正的文化要义在于改变一个人思考的方式、方法、视角，从而最大限度地张扬数学思考的魅力[13]. 建议教材修订要多关注此类问题的处理.

3.2 重视旁注式数学文化内容的呈现，寻找全新的教学视角

旁注往往被“镶嵌”在教材的最需要之处，点拨在学生迷茫处，它与教材正文互相补充、互相衬托，让知识有了更多的增量和意蕴[14]. 旁注中蕴含的丰富的数学文化内容同样可以为教师教学带来许多启示.新教材对知识点的讲解多采用白描式的叙述，其中蕴含的隐性知识和核心价值需要教师挖掘，而旁注中的数学文化常常起到见微知著、画龙点睛的作用. 如教材中平面向量的正交分解概念直接结合平面向量基本定理给出，显得十分突兀.旁注中提供一则斜面上物体重力G的分解方式，若能与之结合联想基底相互垂直这一特殊情形，就能更自然地引出正交分解的概念，让学生更好地理解“选择互相垂直的向量作为基底为研究问题带来方便”的内涵.另外，教材中的某一知识脉络往往会出现多个旁注式数学文化，它们并不是孤立的，而是彼此相关联的，教师要能够洞察其中要义.如“概率”章节的旁注中出现的多处数学文化分别呈现了样本空间、概率、大数定律的史料，从时间线上可以感知，新教材中数学知识出现的先后顺序并不一定就是历史上数学家发现知识的顺序，而是教材为了我们能够系统地学习知识而刻意安排的.反观“概率”教学的环节，应当先通过实验形成概率的统计意义，再引入样本空间，抽象出理想的古典模型.关注旁注式数学文化的作用和价值，让数学教师的教学有了全新的视角，只有用敢于质疑、知行合一的态度用好教材，数学教学才能精益求精，日益完善.3.3 深化数学史的融合程度，避免文化的工具主义倾向

由新教材对数学史的认知水平要求可知，教材中数学史的融合程度不足. 许多研究表明，教师在教学中较少使用数学史，主要原因在于缺乏“直接能用的数学史”.表现在两个方面：一是缺乏相应史料;二是有史料，却不知怎样使用[15]. 究其原因，是现有的数学教材缺失具有教学价值的数学史料，故建议教材修订适当采用顺应式、重构式的数学史运用方式，将古代数学问题改编成符合学生经验的内容和形式，或将数学史料用于知识脉络呈现，深化数学史的融合程度，为教师教学提供更多的思考和选择空间.同时，教师在数学教学中应避免文化的工具主义倾向，不是在数学教学中安放几个文化素材便了事，而应探究多样的数学文化融入数学教学的实践路径，通过跨学科使得数学文化落地生根[16]. 例如，开发数学文化项目学习案例[17]，基于单元整体观融入数学史[18]等.让学生在探究数学规律、掌握数学知识的过程中，感受数学魅力，领会数学精神，受到文化感染，产生文化共鸣，体会文化品位.

参考文献

[1] 吴立宝，寇晨红，王建波.中小学数学教材的属性与功能[J].数学通报，2021，60（10）：1620.

[2] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022：95.

[3] Kline·M.The ancients versus the moderns， a new battle of the books. The Mathematics Teacher，1958，51（06）：418427.

[4] 王嵘.数学文化融入中学教科书的内容与方法[J].数学教育学报，2022，31（01）：1923.

[5] 人民教育出版社，课程教材研究所，中学数学課程教材研究开发中心.普通高中教科书数学必修（A版）[M].北京：人民教育出版社，2019.

[6] 刘鹏飞，徐乃楠，王涛.怀尔德的数学文化思想及评述[J].长春师范大学学报，2019，38（12）：1520.

[7] 黄秦安.数学文化观念下的数学素质教育[J].数学教育学报，2001，10（03）：12.

[8] 张定强，王金燕.“数学文化”研究20年：成果与展望[J].江苏教育研究，2022（Z1）：8186.

[9] 中华人民共和国教育部.普通高中数学课程标准（2017年版2022年修订）[M].北京：人民教育出版社，2020：10.

[10] 王建磐，汪晓勤，洪燕君.中、法、美高中数学教科书中的数学文化比较研究[J].教育发展研究，2015，35（20）：2832.

[11] Stein.M.K.等.实施初中数学课程标准的教学案例[M].李忠如，译，上海：上海教育出版社，2001：326.