形成核心素养 发展理性思维
2022-05-30杜苗苗王文陈美芳
杜苗苗 王文 陈美芳

【摘 要】 本文对2022年安徽省中考压轴题进行探究,在解决已有问题的基础上进行变式拓展,发掘此问题的数学价值,得到关于通过函数教学帮助学生形成核心素养,发展理性思维的教学启示.
【关键词】 核心素养;理性思维;函数
安徽省中考数学压轴题历年以来都是图形与几何领域中关于三角形的问题,2022年是首次出現以函数的常规计算为载体的压轴题.本题题目偏长,内容丰富,重在考察学生的抽象能力、推理能力、模型观念、几何直观和运算能力.题目看似错综复杂,实际有迹可循,解题的本质是通过“函数”研究变量之间的关系,体现了对学生数学核心素养与理性思维的考察.
1 试题呈现
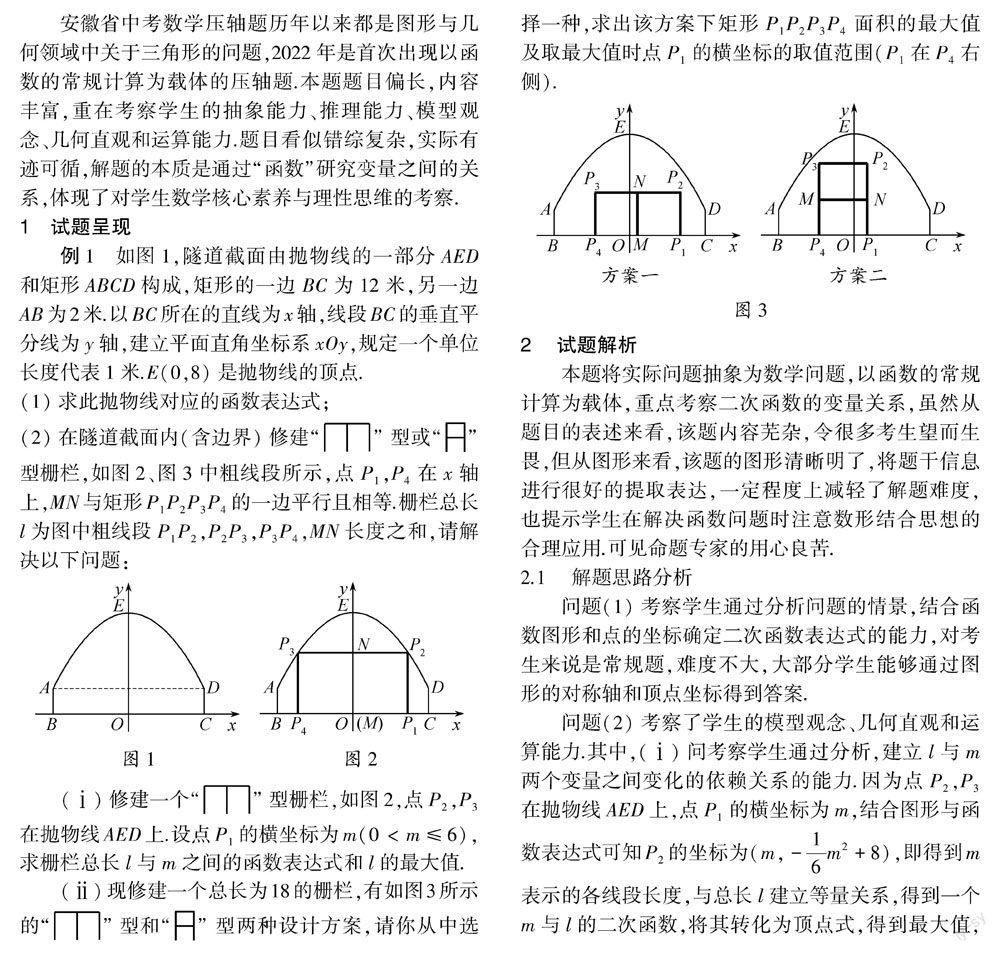
例1 如图1,隧道截面由抛物线的一部分 AED和矩形ABCD构成,矩形的一边BC为12米,另一边AB为2米.以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,规定一个单位长度代表1米.E(0,8)是抛物线的顶点.(1)求此抛物线对应的函数表达式;(2)在隧道截面内(含边界)修建“ ”型或“ ”型栅栏,如图2、图3中粗线段所示,点P 1,P 4在x轴上,MN与矩形P 1P 2P 3P 4的一边平行且相等.栅栏总长l为图中粗线段P 1P 2,P 2P 3,P 3P 4,MN长度之和,请解决以下问题:
(ⅰ)修建一个“ ”型栅栏,如图2,点P 2,P 3在抛物线AED上.设点P 1的横坐标为m(0 (ⅱ)现修建一个总长为18的栅栏,有如图3所示的“ ”型和“ ”型两种设计方案,请你从中选择一种,求出该方案下矩形P 1P 2P 3P 4面积的最大值及取最大值时点P 1的横坐标的取值范围(P 1在P 4右侧). 2 试题解析 本题将实际问题抽象为数学问题,以函数的常规计算为载体,重点考察二次函数的变量关系,虽然从题目的表述来看,该题内容芜杂,令很多考生望而生畏,但从图形来看,该题的图形清晰明了,将题干信息进行很好的提取表达,一定程度上减轻了解题难度,也提示学生在解决函数问题时注意数形结合思想的合理应用.可见命题专家的用心良苦. 2.1 解题思路分析 问题(1)考察学生通过分析问题的情景,结合函数图形和点的坐标确定二次函数表达式的能力,对考生来说是常规题,难度不大,大部分学生能够通过图形的对称轴和顶点坐标得到答案. 问题(2)考察了学生的模型观念、几何直观和运算能力.其中,(ⅰ)问考察学生通过分析,建立l与m两个变量之间变化的依赖关系的能力.因为点P 2,P 3在抛物线AED上,点P 1的横坐标为m,结合图形与函数表达式可知P 2的坐标为(m,- 1 6 m2+8),即得到m表示的各线段长度,与总长l建立等量关系,得到一个m与l的二次函数,将其转化为顶点式,得到最大值,此时要注意自变量的取值范围,则该题得解. 问题(2)的(ⅱ)问,已知栅栏总长l等于18米为图中粗线段P 1P 2,P 2P 3,P 3P 4,MN长度之和,矩形P 1P 2P 3P 4的面积为P 1P 2,P 2P 3之积,故可以设出矩形一边长度,得到一边长度与矩形面积的二次函数,进而求解.题目要求在两种方案中任选一种,如果选择方案一,设 P 1P 2 =x,则 P 2P 3 =18-3x,S= P 1P 2 · P 2P 3 =x(18-3x)=-3x2+18x,求最大值,故化为顶点式S=-3(x-3)2+27,又由题可得当x=3时面积取最大值27,且满足自变量的取值范围.此时矩形的形状大小已定,再求此时点P 1的横坐标的取值范围,结合图象,当矩形的P 2,P 3点分别落在抛物线上时,P 1的横坐标取得最大值和最小值,P 1的横坐标取值范围在此区间内.此时P 2,P 3的纵坐标确定为3,故可以求出当它们分别落在抛物线上时,横坐标分别为± 30 ,当P 2落在抛物线上,P 1的横坐标取得最大值 30 ,当P 3落在抛物线上时,P 1的横坐标取得最小值,P 1P 4的长度为9,故此时P 1的横坐标为- 30 +9.所以最大值时点P 1的横坐标的取值范围为[- 30 +9, 30 ],本题可解.方案二同理可解. 2.2 变式拓展 例2 工人已经在例1所在的隧道内修建了三角形栅栏,如图4所示线段BE和CE,现仍计划修建一个总长为18的栅栏,仍有如图4所示的“ ”型和“ ”型两种设计方案,矩形P 1P 2P 3P 4的长宽均为整数,请你从中选择一种,求出该方案下矩形P 1P 2P 3P 4面积的最大值及取最大值时点P 1的横坐标的取值范围(P 1在P 4右侧). 设计意图 本题将一次函数的知识融入题目,学生会求其表达式,并且考察了学生在求二次函数最大值时是否充分考虑自变量的取值范围,进而帮助学生形成核心素养,发展理性思维. 解 (以方案一为例) 设 P 2P 3 =x,则 P 1P 2 = 18-x 3 ,S= P 1P 2 · P 2P 3 =x· 18-x 3 =- 1 3 x2+6x,化为顶点式S=- 1 3 (x-9)2+27,当 P 2P 3 =9, P 1P 2 =3时,由例1可知B(-6,0),C(6,0),E(0,8),故BE,CE所在直线的函数表达式分别为y 1= 4 3 x 1+8,y 2=- 4 3 x 2+8.当y 1=y 2=3时,x 1=- 15 4 ,x 2= 15 4 ,此时 x 1 + x 2 = 15 2 < P 2P 3 =9,故舍去.由图象知 BC =12,且需要满足矩形P 1P 2P 3P 4的长宽均为整数,故当 P 2P 3 =6, P 1P 2 =4时,y 1=y 2=4,x 1=-3,x 2=3, x 1 + x 2 =6= P 2P 3 满足条件,此时S=24.当 P 2P 3 =3, P 1P 2 =5时,y 1=y 2=5,x 1=- 9 4 ,x 2= 9 4 , x 1 + x 2 = 9 2 > P 2P 3 =3,满足条件,此时S=15<24,故舍去.当 P 2P 3 =12, P 1P 2 =2时, BC =12,此时点P 4,P 1分别与点B,C重合,不满足题意,故舍去.综上所述,方案一下矩形P 1P 2P 3P 4面积的最大值为24,取最大值时点P 1 的横坐标为3. 3 教学启示 初中学业水平考试是国家重要考试之一,中考的试卷分析对改进教师教学和指导学生复习都有着很重要的作用.通过试题可以寻找命题素材的来源,比如本文所展示的2022年安徽中考数学压轴题来源于沪科版九年级数学教材第二十一章第四节二次函数的应用练习题——关于二次函数隧道问题.所以教师在复习时应该紧扣课本,打好基础,再在此基础上进行拓展与发散,不能忽视教材的重要性[1].同样通过分析试题也能得到一些启示. 3.1 教学过程立足学生核心素养发展 例1考察的是二次函数的知識点,也重点考察了学生的抽象能力、推理能力、模型观念、几何直观和运算能力,这些能力是初中数学核心素养的主要表现.数学核心素养是在教学过程中逐步形成和发展的,其中模型观念的形成更离不开函数章节的教学过程.2022年最新修订的《义务教育数学课程标准》明确提出,应使学生通过数学的学习,形成和发展面向未来社会和个人发展所需要的核心素养[2].因此在教学过程中不应该只关注学生对知识的掌握,更应该立足于学生核心素养的发展.例如在函数教学过程中,求函数表达式注意锻炼学生的运算能力,函数图象与解析式相结合注意锻炼学生的几何直观,将现实问题转化为函数问题注意锻炼学生的抽象能力与模型观念,整个函数的解题过程中注意锻炼学生的推理能力等. 3.2 教学活动重视培养学生理性思维 数学在形成人的理性思维中发挥着重要的作用,数学解题的过程是锻炼理性思维的过程.当例1以较大的篇幅出现在考卷最后一题时,缺少理性思维能力的学生已经产生巨大压力,感觉这题难度很大,从而失去解题的信心与耐心.具有较强理性思维的学生可以很快提取题干中的有效信息,并且有理有据一步一步得到答案.所以说理性思维在学习与生活中都很重要,需要教师在教学过程中潜移默化的培养.在教学过程中,教师除了可以指导学生进行推理证明题的训练之外,还可以通过改编题目、设置题组、变式训练、设置开放型题目等方式,锻炼学生的思维能力,要注意打破学生的惯性思维,锻炼学生思维的灵活性和敏捷性. 4 总结 综上所述,安徽省中考数学压轴题改编来源于九年级数学教材,解法中渗透了重要的数学核心素养和理性思维,启示教师在教学时应该把握好教材,在此基础上重视培养学生的数学核心素养和理性思维,使学生在获得“四基”,发展“四能”的基础上形成正确的情感、态度、价值观. 参考文献 [1] 刘清清.立足课本 渗透素养[J].中学教研(数学),2022(02):46-48. [2] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.