新课改二十年来我国中小学概率学与教研究的谱系与前瞻

【摘 要】  通过共词分析、社会网络分析、聚类分析、多维度尺度分析等构建网络图谱，厘清新课改二十年来我国中小学概率学与教研究的谱系.当前的核心议题有：学生概率认知水平及教学策略研究;教师概率知识水平及教学状况调查;概率课程标准及教材的比较研究.基本结论有：学生的概率认知存在诸多迷思概念;教师自身的概率知识状况并不乐观，对学生概率学习的规律缺乏认识;国外教材的若干优秀经验值得借鉴.未来研究的方向有：学生迷思概念的发展及其干预;低龄儿童概率前概念的诊断;教师概率知识及KCS的培养;教材的任务设计和学习路径研究.

【关键词】  概率;认知水平;迷思概念;课程标准;社会网络分析

1   问题提出

自PISA项目数学素养框架设计组主席、弗莱登塔尔研究所所长朗格（Lange）提出关于“不确定性”的素养以来[1]，概率素养（probability literacy）逐渐引起数学教育研究者的关注，已然成为近几届国际数学教育大会概率學习与教学专题研究小组的核心议题[2][3].

2001年，教育部颁布《全日制义务教育数学课程标准（实验稿）》（以下简称《课程标准（实验稿）》），首次将概率作为核心内容领域之一纳入中小学数学课程的体系之中[4].经过《义务教育数学课程标准（2011年版）》的修订[5]，概率内容的课程编排整体后移，难度得以降低、层次得以凸显[6][7].类似地，《普通高中数学课程标准（2017年版2020年修订）》在课程编排中淡化了原有的模块化设计，凸显了概率内容的发展主线[8].2022年，教育部颁布《义务教育数学课程标准（2022年版）》（以下简称《课程标准（2022年版）》），在概率内容的课程编排上进一步关注了其对于学生认知发展的适切性[9].

概率内容进入我国课程标准已逾二十年.在这二十年里，我国数学教育领域围绕中小学概率的学与教做了哪些方面的研究？这些研究取得了哪些主要结论？未来研究可做哪些更深入的探索？本研究基于科学计量学与信息可视化技术，厘清二十年余（2001～2021）我国中小学概率学与教研究的核心议题，探索未来研究的可能方向，以期为从事该领域教学及研究的同仁提供有益参考.

2  研究过程与方法

2.1 数据来源

数据资料全部来源于中国知网（CNKI）数据库.研究者先后选择中文核心期刊和数学教育专业博、硕论文进行检索.考虑到选择数据库时已然限定了学科范围（即“中等教育”和“初等教育”），因此直接用“概率”作为主题检索词，以尽可能多地搜集到强关联的相关研究.最终共搜集有效文献219篇，其中期刊论文50篇，学位论文169篇.

2.2 分析过程

本部分工作采用Bicomb软件、Ucinet 6软件及SPSS 22.0统计软件协同展开.第一步，确定搜索主题及导出相关文献.第二步，提取关涉文献的关键词.第三步，采用Bicomb软件统计上述219篇文献的关键词，结果显示有452个关键词.结合研究需要，以词频大于6的关键词为阈值节点，“6≤频次阈值≤47”的高频关键词共计27个.第四步，利用Bicomb软件的共词分析功能生成高频关键词词篇矩阵和共现矩阵.第五步，利用Ucinet 6软件绘制网络图谱.第六步，将高频关键词词篇矩阵导入SPSS 22.0进行聚类分析，并对共现矩阵进行多维度尺度分析.第七步，结合聚类分析和多维尺度分析数据报表，厘清核心议题.

3  研究结果

3.1 高频关键词词频统计

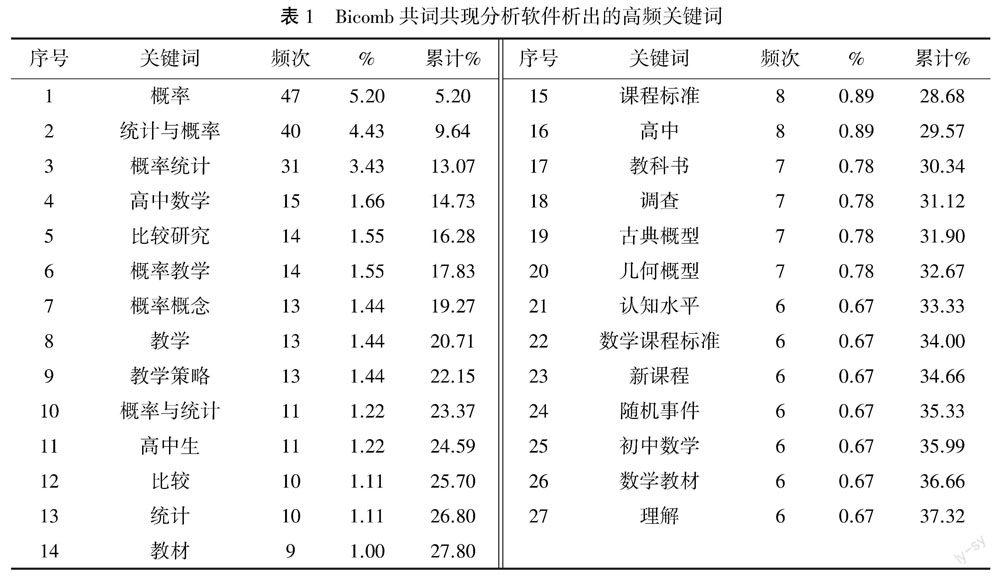
上述219篇文献的关键词分析显示共有452个关键词，将其中前27个高频关键词（频次≥6）抽取出来，其频次排序如表1所示.从该表大体可见，除去主题词“概率”以及“统计与概率”等捆绑词条，高中数学、比较研究、概率教学等都是新课改二十年来我国中小学概率学与教研究的核心议题.值得注意的是，当前研究大多聚焦于高中阶段（“高中生”“高中”等均是高频关键词），而针对初中和小学阶段的研究则相对较少.

3.2 社会网络分析

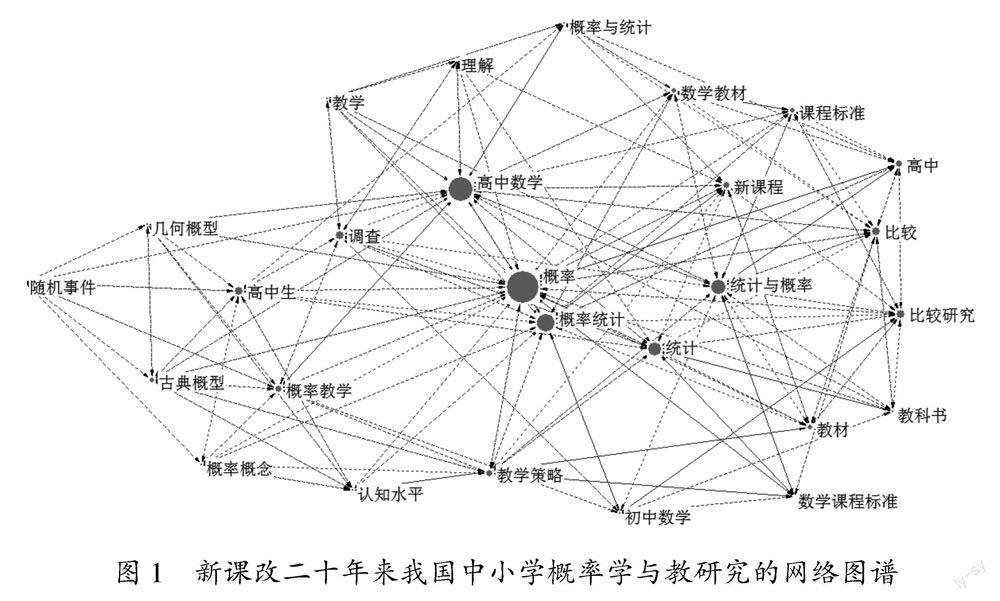
对析出的27×27高频关键词共现矩阵进行分析，运行Ucinet 6软件得到上述高频关键词为节点的网络图谱，详见图1.在该图谱中，每个节点分别表示一个高频关键词，并且节点的大小表示其在网络图谱中的影响力;节点间的连线表示高频关键词之间的联系.从节点大小及连线密疏能大体发现：当前研究主要围绕“概率”“高中数学”“概率统计”等关键词展开，并且由之向其他议题延伸.例如，与“概率”直接密切关联的关键词有课程与教材层面的“高中数学”和“数学教材”;教学层面的“概率教学”和“教学策略”;学习层面的“理解”和“认知水平”;内容本身层面的“几何概型”和“古典概型”等.进一步，“概率”所关联的关键词彼此之间又存在二次关联，从而进一步拓展了研究议题.

3.3 高频关键词聚类分析及多维尺度分析

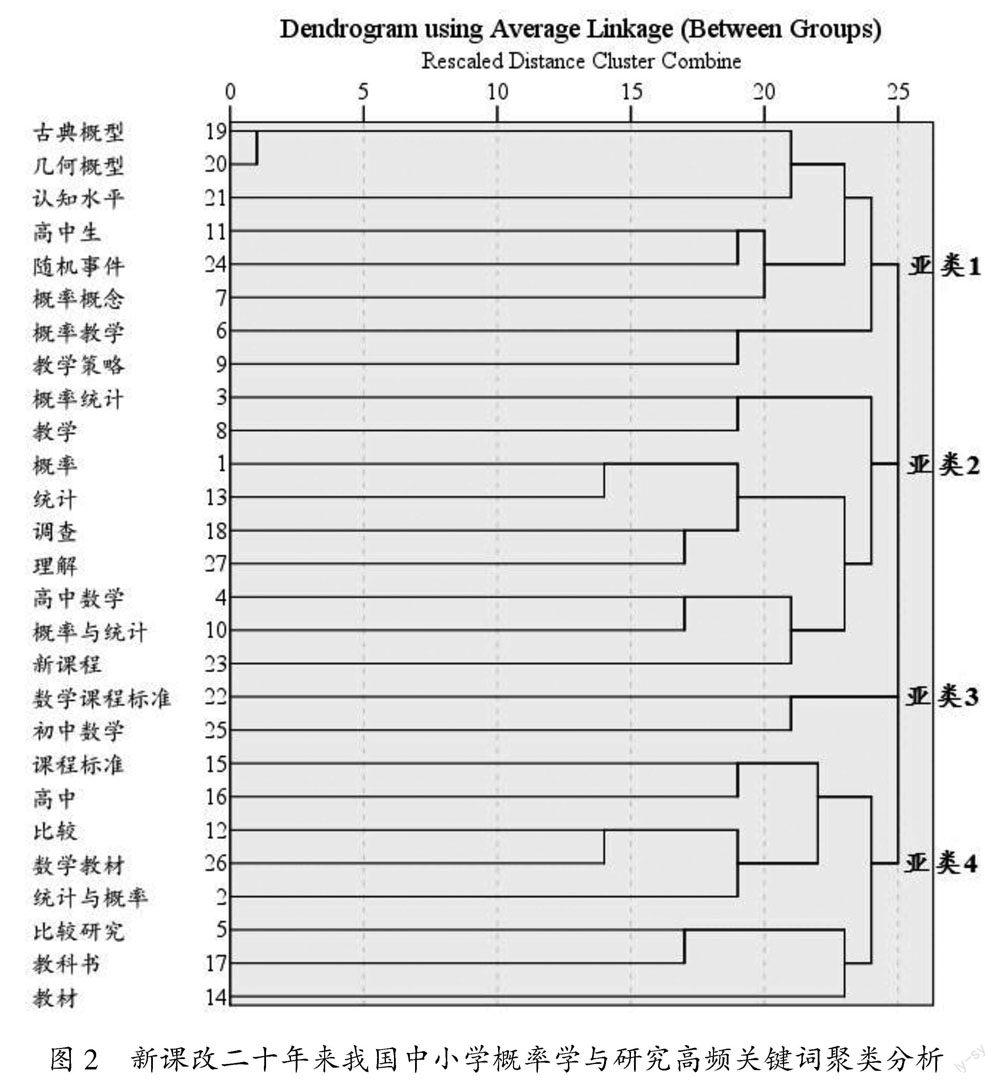
对高频关键词的相似系数矩阵进行系统聚类分析.根据聚类分析类团连线距离的远近将其划分为四个亚类，其结果详见图2.     图2 新课改二十年来我国中小学概率学与研究高频关键词聚类分析     根据多维尺度分析中的ALSCAL分析法对研究关键词间的学术联系进行考察.结果表明，模型距离解释的百分比RSQ=0.617（>0.6），达到可接受范围.通过对上述四个亚类关涉关键词的关系梳理，凝练新课改二十年来我国中小学概率学与教研究的核心议题，详见表2.

亚类1是学生概率认知水平及相应教学策略方面的研究，由两方面组成：子类1为学生概率认知水平，包括古典概型、几何概型、认知水平等关键词;子类2为概率内容教学改进方面的研究，包括概率教学、教学策略等关键词.亚类2是教师概率知识及教学现状方面的研究，由两方面组成：子类1为概率教学现状方面的研究，包括概率统计、教学等关键词;子类2为教师概率知识方面的研究，包括概率、调查等关键词.亚类3是概率内容课程标准方面的研究，包括数学课程标准、初中数学等关键词.亚类4是课程设置及教材编写的比较研究，包括课程标准、比较、数学教材等关键词.其中，亚类3和4可以进一步合并为“概率课程标准及教材的比较研究”.

4  讨论与分析

4.1 新课改二十年来我国中小学概率学与教研究的核心议题

4.1.1 学生概率认知水平及教学策略研究

上世纪八十年代，张增杰等在国内率先开展了“儿童概率概念认知发展”的大规模调查[10][11]，证实并丰富了皮亚杰（Piaget）关于“儿童概率概念认知发展阶段”的观点[12].在数学教育领域，李俊在其博士论文中率先基于SOLO分类理论提出了一个“认知概率概念的发展框架”[13]，该成果随后被翻译成中文出版[14]，成为国内概率学与教研究的经典著作.

概率内容自2001年“飞入寻常百姓家”.如果以该年作为一个时间节点，有关中小学概率学与教的研究开始零星出现.在《课程标准（实验稿）》颁布实施的伊始几年（2001～2005），研究者便开始就概率内容的目标定位[15]、知识编排[16]、实验效果[17]等进行了理论和实证的分析，由此也引起了学界对于“概率内容目标定位与学生认知水平间适切性”的热烈讨论[18].在此背景下，有关“概率认知水平”的实证研究开始引起学界重视.例如，华东师范大学亚洲数学教育中心李俊博士就曾指导其硕士研究生陆续开展了多项研究，系列成果近期也已正式出版[19].

总体而言，有关学生概率认知水平的实证研究基本围绕“水平划分”“认知障碍”“迷思概念”“教学对策”等议题展开.梁常东等人在其研究中证实了国外实证研究中报道的等可能性偏见、代表性启发等典型的迷思概念[20].等可能性偏见是指在比较两个或多个事件的概率时，人们倾向于认为“所有事件的概率总是相等的”“机会是‘一半一半的”[21].例如，同时掷两枚均匀的骰子，持等可能性偏见的学生会认为结果“5和6”和“两个6”的概率是相等的.代表性启发是指人们在概率决策时倾向于相信一个“代表性的结果”更容易出现.例如，连续抛一枚均匀的硬币六次，持代表性启发的学生会认为序列“正、反、正、反、反、正”的概率比序列“正、正、正、正、反、正”的大，因为“前者的正面和反面出現的频次相当，看起来也更加随机、更加有代表性”[22].有趣的是，这种迷思概念在职前教师和在职教师中都广泛存在[23][24].

近年来，有研究对我国学前至初中阶段学生的概率认知发展进行了较系统的考察：从“认知发展速度”的视角将其划分为缓慢发展时期、快速发展时期、停滞发展时期等发展阶段[25];采用拉什（Rasch）模型刻画了学生概率学习从定性认识到定量认识的进阶规律[26];通过跨年级比较发现了学生的迷思概念常常十分顽固、难以消除[27]，但是在直观的任务情境中，低学段学生对于高阶内容的认知也能有较好的直觉[28].

学生概率认知的局限性是客观存在的，这也得到了国外研究的支撑[21-24].教学既要尊重学生的迷思概念，又要尽可能地帮助其摆脱这些认知局限.综合来看，有关“概率认知水平”的实证研究大都针对性地提出了教学建议.例如，科学规划概念学习的步次，精心设计层层递进的任务[26]，通过直观生动的动画模拟提供真实的概率情境[20].实证研究表明，在数学游戏[29]、计算机辅助教学[30]、增强现实技术[31]等情境中，学生能够更好地理解概率.

4.1.2 教师概率知识水平及教学状况调查

除了学生对于概率的迷思概念以外，教师对概率基本概念及思想方法的错误认识也不容忽视.程伶俐的调查研究显示：教师常常过于偏爱采用排列、组合或树状图等理论方法来计算概率，而鲜有主动提出通过模拟试验等方法及利用频率与概率的关系来估计概率;鲜有教师真正了解概率的公理化定义及其产生背景;“简单复合法”“预言结果法”等迷思概念在教师中广泛存在[32].值得注意的是，教师概率认知的局限性在国外研究中也有报道[24][33].

教师自身概率知识的薄弱是导致当前概率教学问题的重要原因.正如谢琳等人所认为的：当前概率教学中两个令人担忧的现象是，一方面教师轻视基本概念和随机思维的教学，另一方面他们自身的概率知识薄弱、概率素养缺乏，而这两方面通常互为因果[34].教师概率教学中的问题或困惑是比较普遍的，他们常常在教学中把过多的注意力放在了概率的本质内容之外.例如，有的教师在概率教学时过于追求计算，而忽略了引导学生理解概念的本质.有的教师过分强调“只有把排列组合这个工具学好，才能把样本空间的概念说清楚”.甚至有教师反映：“没有排列组合的知识作为铺垫，概率内容难以进行下去——因为概率就是‘计算.”[34]何小亚指出，教师在概率教学中往往连“我们为何要学习古典概型”这一基本问题都没有向学生解释清楚[35].此外，有研究认为教师在概率教学时应帮助学生摆脱确定性思维方式的枷锁，引导其在思维层面建立随机观念[36].

4.1.3 概率课程标准及教材的比较研究

他山之石，可以攻玉.从关涉国别来看，当前有关概率课程及教材的比较研究多聚焦于中国与发达国家之间的对比[37][38].此外，近年来多国别之间的综合比较研究也已出现[39][40].综合来看，当前的此类研究多聚焦于内容定位、教材编排、呈现方式等方面，对了解国际课程改革的发展趋势及吸收国外优秀经验提供了直接参考.例如，中美两国初中课程标准的对比显示，两国都强调了概率与统计内容的关联性，鼓励通过数据收集等统计活动沟通上述两方面知识[37].中法两国高中课程标准的对比显示，我国课程更强调对随机概念的认识，而法国则侧重于理论与计算，因此我国课程可进一步加强概率内容与其他学科之间的联系[41]，另有其他研究也提出了类似建议[7].中澳两国初中课程的比较表明，我国课程标准中的表述严谨性尚待加强[42].

值得注意的是，国际比较研究的目的是博采众长、去粗取精，绝非妄自菲薄、盲目效仿.有关概率内容的编排设计、认知要求等问题，我们应在吸收国际优秀经验的同时，合理、客观地分析自身的优势和缺陷.例如，吕世虎等通过对中、新两国初中教材的比较研究指出：我国教材就“随机事件”“可能性”等核心概念设计的习题明显多于新加坡教材，这说明我国教材更加重视基本概念，值得发扬;但是情境性强、高层次的习题则显然不足[38].

4.2 未来研究的可能方向

基于对新课改二十年来相关研究的梳理，对未来研究提出以下建议.

4.2.1 学生迷思概念的发展及其干预

有关学生概率认知的实证研究证实了我国中小学生对于概率的认知存在诸如等可能性偏见、预言结果法等迷思概念.接下来的问题是：这些迷思概念在学生的学习过程中是如何发展的？哪些迷思概念在学生的概率认知过程中根深蒂固？哪些则是可以通过恰当的教学干预得以显著消除？教学如何帮助学生摆脱这些迷思概念？目前尚缺乏这些方面的实证研究.

4.2.2 低龄儿童概率前概念的诊断

纵观新课改二十年来我国中小学概率学与教研究的相关研究，其研究对象更多地关注于高中阶段，初中阶段次之，而有关小学、学前阶段的研究甚少.儿童在接触学校正式的概率知识之前，已然积累了或多或少、或对或错的非正式知识（informally acquired knowledge）或前概念（preconception），国外研究已然对此进行了一些探索[29][43].这些前概念有些是有一定合理性，有些则是与正式的概率知识相冲突的.问题是：当学生带着这些前概念走进学校时，课程、教学应该怎样在尊重其前概念的前提下帮助其发展正式的概念？只有厘清了低龄儿童的概率前概念，才能在小学阶段设计课程目标、内容定位时更加有据可循.也只有这样，我们才能让孩子在第一次接触概率知识时就感到舒适、自然.但总体而言，国内目前的相关研究甚少.例如，林泳海的研究表明：6.5岁儿童的概率概念基本处于萌芽状态，7.5岁儿童则开始发展部分概率概念[44].更进一步地，小学低段学生的概率认知水平如何？有哪些前概念？尚待做更细致的研究.

4.2.3 教师概率知识及KCS的培养

“给学生一瓢水，教师得要有一桶水”.遗憾的是，国内外的实证研究都一再证实，教师自身的概率知识尚显薄弱，各类迷思概念也比较突出[33][45][46]，在概率教學中常常忽略概率思想和本质内容的渗透[35].有关职前教师的概率知识的调查研究也表明，等可能性偏见等迷思概念同样广泛存在[47].鉴于以上，建议在概率思想的理解、概率知识的储备及概率发展史的渗透等方面加强教师培训.需要注意的是，仅补足教师的概率知识还远远不够.Hill等在其提出的MKT框架中指出：除了学科知识以外，教师还应具备扎实的教学内容知识，其中内容与学生知识（Knowledge of Content and Students，简称KCS）就是一个重要方面，它一般包括“教师对学生学习过程、运算策略、常见错误等的理解”[48].换言之，教师除了自身概率知识扎实以外，还应关注“学生是如何学习概率的”.当前有关这方面的研究还不多，其基本结论是：教师对学生概率学习的规律缺乏认识，不了解其概率认知中的困难[45].教师常常感到“概率难教”，与此有很大关系.为此，建议未来研究着眼于教师关于概率内容的KCS研究，并致力于提高其概率教学的水准.

4.2.4 教材的任务设计和学习路径研究

教材文本及其比较研究一直是数学教育领域的热点研究方向之一.概率领域的研究同样如此，且此类研究通常聚焦于内容的呈现方式、难易程度、例题习题等.自新课改以来，教材里的概率内容在编排上越来越凸显层次设计和发展主线，也越来越强调内容对于学生认知规律的适切性.随着《义务教育数学课程标准（2022年版）》的颁布，各版本教材的修订工作行将展开，未来教材将如何落实上述编排理念？研究者认为，微观视角下进阶式的数学任务和宏观视角下递进式的学习路径将是未来教材及其比较研究的两个出发点.第一，可从上述两个视角出发就当前教材进行文本分析;第二，可基于实证研究对当前教材的任务设计和教学路径提供有益建议;第三，对于比较研究而言，从上述两个视角开展不同教材文本及不同教材教学效果等方面的对比分析也是值得关注的研究方向.  5  结语

概率内容走进我国中小学数学课程的时间不长，国内数学教育领域有关该方面的实证研究相对较少.近两年来，有学者就当前概率课程、教材及教学方面存在的具体问题提出了中肯建议[49]，有关概率学与教的研究任重而道远.本文提出的未来研究方向供数学教育研究的同仁参考.

参考文献

[1] Lange J. Mathematical literacy for living from OECD-PISA perspective [J]. Tsukuba Journal of Educational Study in Mathematics， 2006 （25）： 13-35.

[2]  Nilsson P， Li J. Teaching and Learning of Probability [M] In Cho S J. The Proceedings of the 12th International Congress on Mathematical Education： Intellectual and Attitudinal Challenges. New York： Springer， 2015： 437-442.

[3] Batanero C， Chernoff E J， Engel J， et al. Topic Study Group No. 14： Teaching Learning of Probability [M] In Kaiser G. The Proceedings of the 13th International Congress on Mathematical Education. Springer， 2017： 439-442.

[4] 中华人民共和国教育部. 全日制义务教育数学课程标准（实验稿）[M]. 北京：北京师范大学出版社，2001：1-8.

[5] 中華人民共和国教育部. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012：1-20.

[6] 史宁中，马云鹏，刘晓玫. 义务教育数学课程标准修订过程与主要内容[J]. 课程·教材·教法，2012，32（03）：50-56.

[7] 张楠. 中美义务教育数学课程标准“统计与概率”领域的比较研究[J]. 数学教育学报，2014，23（01）：88-91.

[8] 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.

[9] 中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.

[10] 张增杰，刘范，赵淑文，等. 5～15岁儿童掌握概率概念的实验研究：儿童认知发展研究（II）[J]. 心理科学通讯，1985，1985（06）：1-6.

[11] 张增杰，刘中华，邱曼君. 5—11岁儿童概率概念认知结构的萌芽及其发展[J]. 西南师范学院学报（自然科学版），1983（02）：29-43.

[12]  Piaget J，Inhelder B. The origin of the idea of chance in children [M]. New York： Norton， 1975.

[13]  Li J. Chinese Students Understanding of Probability [D].  Singapore：Doctoral Dissertation of Nanyang Technological University， 2000： 183-185.

[14] 李俊. 中小学概率的教与学[M]. 上海：华东师范大学出版社，2003.

[15] 章飞. 义务教育阶段概率有关知识的内容定位与教材实施[J]. 数学教育学报，2004，13（01）：48-51.

[16] 蔺云. 对义务教育实验教科书中概率内容的评述[J]. 数学教育学报，2005，14（04）：95-97.

[17] 刘福林. 小学数学新教材“统计与概率”的实验效果调查分析[J]. 数学教育学报，2004，13（03）：56-57.

[18] 吕建生. 生活先于课程将统计概率推到了学生的面前[J]. 数学通报，2003（10）：34-36.

[19] 李俊. 中小学概率统计教学研究[M]. 上海：华东师范大学出版社，2018.

[20] 梁常东，唐剑岚. 中学生概率学习中的错误及其教学策略[J]. 数学教育学报，2007，16（02）：98-102.

[21] Rubel L H. Middle school and high school students probabilistic reasoning on coin tasks [J]. Journal for Research in Mathematics Education， 2007， 38（05）： 531-556.

[22] Morsanyi K， Primi C， Chiesi F， et al. The effects and side-effects of statistics education： Psychology students （mis-）conceptions of probability [J]. Contemporary Educational Psychology， 2009， 34： 210-220.

[23] Chernoff E J. Recognizing revisitation of the representativeness heuristic： an analysis of answer key attributes [J]. ZDM， 2012， 44（07）： 941-952.

[24] Hokor E K， Apawu J， Owusu-Ansah N A， et al. Preservice Teachers Misconceptions in Solving Probabilistic Problems [J]. Pedagogical Research， 2022， 7（01）： em0112.

[25] 巩子坤，何声清. 6～14岁儿童的概率概念认知发展[J]. 教育研究与实验，2017（6）：83-88.

[26] 何声清，巩子坤. 6～14岁儿童概率概念学习进阶[J]. 课程·教材·教法，2017，37（11）：61-67.

[27] 何声清，巩子坤. 7～9年级学生概率比较的策略及其发展[J]. 数学教育学报，2017，26（02）：41-45.

[28] 何声清. 六年级学生对高阶概率内容的认知：潜能与局限[J]. 数学教育学报，2018，27（03）：57-61.

[29] Nikiforidou Z， Pange J， Chadjipadelis T. Intuitive and informal knowledge in preschoolers development of probabilistic thinking [J]. International Journal of Early Childhood， 2013， 45（03）： 347-357.

[30]  Pratt D. Making sense of the total of two dice [J]. Journal for Research in Mathematics Education， 2000， 31（05）： 602-625.

[31] Cai S， Liu E， Shen Y， et al. Probability learning in mathematics using augmented reality： impact on students learning gains and attitudes [J]. Interactive Learning Environments， 2020， 28（05）： 560-573.

[32] 程伶俐. 中学数学教师对概率概念及其教学的认识[D]. 上海：华东师范大学，2006：18-48.

[33]  Liu Y， Thompson P. Teachers understanding of probability [J]. Cognition and Instruction， 2007， 25 （02）： 113-160.

[34] 谢琳，刘剑涛. 从两个争议看高中概率论基本概念教学中存在的问题[J]. 数学教育学报，2010，19（06）：6-8.

[35] 何小亚. 高中概率模型学与教中的问题和对策[J]. 数学教育学报，2017，26（01）：37-40.

[36] 钟志华. 对高中新课程中概率教学的认识[J]. 数学教育学报，2006，15（01）：82-85.

[37] 刘长明. 中美初中学段“统计与概率”领域内容标准的比较研究[J]. 数学教育学报，2004，13（01）：67-70.

[38] 吕世虎，孙学敏. 中国与新加坡初中数学教材中概率习题的比较研究[J]. 数学教育学报，2010，19（06）：70-73.

[39] 曹一鸣，王万松. 高中概率统计内容设置的国际比较：基于15个国家数学课程标准的研究[J]. 数学教育学报，2016，25（01）：1-4.

[40] 蔡庆有，黄燕苹，金美月，等. 中日韩小学数学教材内容的对比研究[J]. 课程·教材·教法，2014，34（07）：114-120.

[41] 李红玲，张玉环. 中法课标中概率统计内容的比较分析[J]. 数学教育学报，2014，23（05）：60-64.

[42] 张维忠，陈虹兵. 中澳数学课程标准内容深度比较：基于初中学段“统计与概率”的分析[J]. 教育学报，2012，8（05）：29-36.

[43] Tatsis K， Kafoussi S， Skoumpourdi C. Kindergarten children discussing the fairness of probabilistic games： The creation of a primary discursive community [J]. Early Childhood Education Journal， 2008， 36（03）： 221-226.

[44] 林泳海，张茜，任培晓. 5.5～7.5岁儿童概率认知发展的试验研究[J]. 鲁东大学学报（哲学社会科学版），2011，28（03）：83-88.

[45] 何声清. 数学教师KCS与学生认知的一致性研究：以“概率”内容为例[J]. 数学教育学报，2019，28（01）：25-29.

[46] Chernoff E J， Russell G L. The fallacy of composition： Prospective mathematics teachers use of logical fallacies [J]. Canadian Journal of Science， Mathematics and Technology Education， 2012， 12（03）： 259-271.

[47] 杨芳. 职前教师对概率概念的理解研究[J]. 数学教育学报，2013，22（06）：37-40.

[48]  Hill H C， Ball D L， Schilling S G. Content knowledge： Conceptualizing and measuring teachers topic-specific knowledge of students [J]. Journal for Research in Mathematics Education， 2008， 39 （04）： 372-400.

[49] 曹广福，罗荔龄. 中學数学部分概率内容的教学策略[J]. 数学教育学报，2018，27（05）：17-24.