2022年中考数学创新型试题的类型与教学建议

【摘 要】  中考数学创新型试题主要表现为问题探究型、阅读理解型、反思整改型、文化浸润型、审美立美型、知识融合型、动态思维型、直觉思维型、实践与综合应用型等.以2022年全国数学中考试题中的创新型试题为研究对象，对它们进行分类，在每一类中精选典型试题，并对这些创新型试题的立意及考查内容作了说明，提出相应的教学建议.

【关键词】  中考数学;创新型试题;教学建议

《义务教育数学课程标准（2022年版）》在评价建议中提出：“学业水平考试的命题应适当提高应用性、探究性和综合性试题的比例，题目设置要注重创设真实情境，提出有意义的问题，实现对核心素养导向的义务教育数学课程学业质量的全面考查.”随着新一轮课程改革的推进，中考数学命题将会越来越重视通过创新型试题考查学生的创新意识和实践能力.中考数学创新型试题有问题探究型、阅读理解型、反思整改型、文化浸润型、审美立美型、知识融合型、动态思维型、直觉思维型、实践与综合应用型等类型.以2022年全国各地区中考中的创新型试题为研究对象，对它们进行分类，在每一类中筛选典型试题，并对这些创新型试题的立意及考查内容作了说明，提出相应的教学对策.

1  问题探究型

问题探究型试题（见表1）的题干叙述较长，一般先介绍某个命题，然后以问题和变式的形式引导学生对该命题进行某些探究，考查学生阅读理解、猜想发现、推理证明等能力.

教学建议  教师在平时的教学中应深挖教材的创新资源，有意识地引导学生掌握“问题（实验）—探索—证明—推广—应用”的学习方式.如平行四边形性质的证明，垂径定理的证明，一次函数的概念，二次函数与一元二次方程的关系等.注重研究性问题的变式和推广，以问题串的形式引导学生在问题解决过程中深度理解知识.

2  阅读理解型

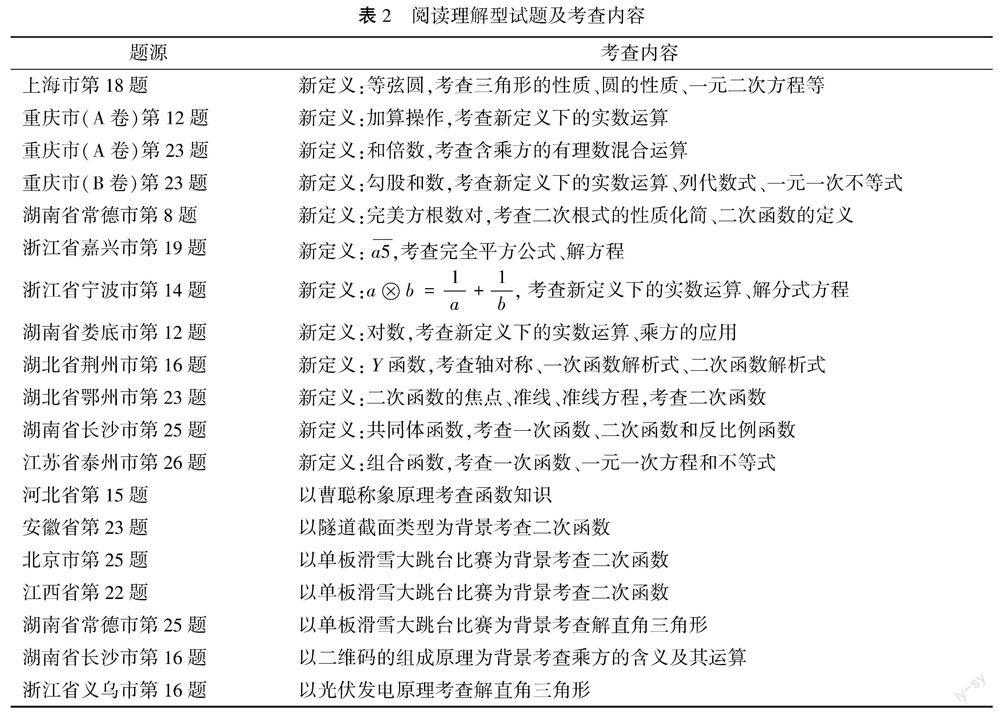
阅读理解型试题（见表2）取材广泛，要求学生阅读材料，理解内容，运用新知解决问题.此类试题往往信息新颖、阅读量大，需要学生短时间内筛选重要信息，理解新概念、新命题，能够很好的考查学生的阅读能力、自学能力、迁移能力等.因此，阅读理解型试题（又称“新定义”试题）已成为中考的热点题型之一.

教学建议   可采取心理学中的系统脱敏法，如精选此类试题让学生集中练习，让学生消除对未知的、复杂的数学符号、概念、命题、图形的焦虑或恐惧，从而有一个清晰的思维来理解“新定义”，提高解題效率.

3  反思整改型

反思整改型试题（见表3）需要学生主动反思并修正错误.目前这类试题较少出现，但这类试题有利于考查学生对数学本质的理解，有利于增强学生的质疑批判意识.

教学建议  这类试题命制的陷阱往往是学生常犯的错误，因此课堂上应留给学生表达的机会，数学语言表达是暴露其数学思维的绝佳方法，教师及时引导学生质疑、反思、纠正其错误.  4  文化浸润型

文化浸润型试题（见表4）是想通过数学文化（主要是数学史）的育人功能达到文化育人的目的.数学史是在数学产生、发现（创造）、发展过程中归纳总结出来的数学史料，是学生感受数学先贤们探索创新精神的“故事会”，是传播数学思想方法的优秀读物，是深化数学学科育人的“好教材”，对增强学生对数学价值的认同和中考数学命题改革都有重要意义.数学文化浸润型试题已成为中考命题的亮点和热点.

教学建议  对于数学创新来说，数学史研究具有指引作用[1].教师应广泛涉猎数学历史素材，能够在新课的引入、课堂习题和课后阅读的布置中运用相关的数学史材料，而且要注重其运用细节，融汇教学内容，才能发挥数学史的教育功能.

5  审美立美型

审美立美型试题（见表5）除了一般审美的感性直观，还具有理性和逻辑成分.数学的感性美表现在结构形式的对称美、规律结论的简洁美、创新思维的奇异美等方面;数学的理性美表现在逻辑推理的严谨美、数学计算的准确美、知识体系的统一美等方面.学生发掘试题中数学美的信息，是解决此类试题的优选策略和有效方法.数学家克莱因认为：“进行数学创造的最主要驱动力是对美的追求.”因此，审美立美型有利于考查学生的创新思维.

教学建议  引导学生爱美、识美、审美、赏美、悟美、立美的前提是教师提高对数学的审美意识，用一颗发现美的心去寻找隐藏在生活、数学结构形式、数学思维方式、数学思想方法中的美.例如，结合熟识的世界名画、雕塑、建筑欣赏黄金比例的美，结合诗词的对仗欣赏数学对偶关系的美，结合音律欣赏数学体系的和谐美.

6  学科融合型

学科融合型试题（见表6）凸显数学学科知识、数学方法和数学思想的融为一体和本质联系，将相互联系的知识、跨学科的知识组织起来，考查学生从整体上理解数学和知识迁移的能力.

教学建议  将教学内容耦合关联，从单一学科教学、单一课时教学转向学科融合教学、单元整体教学.例如，在函数单元的教学中，可联系物理的速度与速率、电阻与电流、压强，化学的密度、溶解度、质量分数，生物的细胞分裂、光合作用等知识.

7  动态思维型

动态思维型试题（见表7）需要学生根据变化的问题情境和条件，及事物发展的联系性特征和动态性特征，来改变自己的思维活动，使问题得以解决.考查学生用变化发展的数学眼光看问题，利用数形结合、动静结合的动态思维解决问题的能力.

教学建议  辩证唯物主义认为，客观世界具有物质性、运动性、规律性、可认知性.教师应用辩证的观点看数学和数学教学：“运动性”对应于“数学里变量、函数变化观点”;“规律性”对应于“数学思维的规律性和数学关系的规律性”;“认知性”对应于“数学是可认知、可探究、可发现的”[2].

8  直觉思维型

直觉思维型试题考查学生的数学直觉思维，即学生可以仅依据其直观感觉、顿悟、灵感而迅速地对问题作出判断、猜想、下结论，而不是依靠逻辑推理[3].直覺思维可以帮助学生分析数学现象、猜想数学命题、顿悟解题思路、缩短思维过程、培育数学灵感等[4].由于直觉思维是创造思维的基础，因此直觉思维型试题有助于考查学生的创新意识和创造能力.

例1  （2022年广东省深圳市第10题） 如图1所示，已知三角形△ABE为直角三角形，∠ABE=90 ° ，BC为圆O切线，C为切点，CA=CD，则△ABC和△CDE 面积之比为（  ）.

A.1∶3 B.1∶2 C. 2 ∶2 D.（ 2 -1）∶1

评析  由经验作出辅助线（图2），根据直观感觉，将 ∠E 特殊化为30°，从而可以迅速选出答案B，缩短思维过程.

教学建议  直觉思维的培养不仅需要学生有良好的认知结构，还需引导学生从宏观上对数学对象进行观察，从数学美的角度看待问题，并鼓励学生联想、猜想和估算.  9  实践与综合应用型

实践与综合应用型试题（见表8）是指具有实际背景的、以综合性问题解决为内容的数学问题，解题关键在于弄清问题情境背后的关系.这类试题是渗透全面发展的创新型人才教育、消防安全教育、智育、劳动教育、体育等的载体，有助于考查学生提炼信息、用数学解决现实问题的能力和数学综合素质.因此，逐渐成为各地中考的亮点和热点.

教学建议  “综合与实践”作为初中数学课程的四大领域之一，是发展学生数学综合素养的重要途径和环节.2022年版新课标中指出“综合与实践”领域应以主题式学习和项目式学习为主，注重实际问题的解决，并将部分知识内容融入其中[5].因此，教师应有基于知识又超越知识的目标追求、基于教材又超越教材的活动内容编排、基于课堂又超越课堂的综合实践活动设计，重在让学生积累活动经验，提高问题解决能力[6].例如，调查某次数学测验的答题情况，各组经过数据整理后，用不同的统计表、统计图进行表示，并指出其中的常用统计量，最后提炼信息对教师提出教学建议、对自己和同桌提出如何改进学习的方法.

数学创新型试题为教师和学生践行“为创新思维而教”“为创新思维而学”指明了方向.研究发现，山西省、浙江省嘉兴市、湖北省、湖南省的创新型试题值得关注.

参考文献

[1] 张奠宙，宋乃庆.数学教育概论[M].北京：高等教育出版社，2016：122.

[2] 刘艺，赵思林.孙维刚的数学教育观与启示[J].中学数学杂志，2021（01）：5-9.

[3] 赵思林，李雪梅.高考数学创新型试题的若干类型与评析[J].内江师范学院学报，2018，33（02）：27-33.

[4] 赵思林，朱德全.试论数学直觉思维的培养策略[J].数学教育学报，2010（01）：23-26.

[5] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[6] 张伟俊.数学“综合与实践”活动的有效设计研究[J].上海教育科研，2018（10）：82-86.