浅析数学美在初中数学教学中的应用

陈宽政

[摘  要] 数学美是想象与理性思维的有机结合，它随着社会发展的需要而诞生. 文章具体从以下三方面谈谈数学美在数学教学中的应用：展示和谐美，激发求知欲;探究简洁美，培养数学思想;感知抽象美，启发数学思维.

[关键词] 数学美;和谐美;简洁美;抽象美

数学是社会发展的产物，是人类赖以生存的文化基础. 古往今来，很多数学家认为数学不仅为生活服务，还处处闪耀着美的光辉. 毕达哥拉斯曾高度称赞：数学的球体与圆拥有对称美，整数如宇宙一样具备和谐统一的美. 普洛克拉斯曾经提出：有数学的地方就拥有美. 罗素则认为：数学不仅拥有真理，还拥有至高无上的美. 文章对数学美在教学中的实际应用谈一些拙浅的看法.

展示和谐美，激发求知欲

数学的和谐美体现在结构严谨、语句雅致、排列整齐等方面. 塞尔伯格曾说，他喜欢数学的动机在于它有如风景图一样美的公式与结构，如奇数1，3，5，

7…，偶数2，4，6，8…. 这些都是属于和谐美的表现，它带给我们结构均衡的视觉感，学生可从事物的对称性中感受到数学的节律性或周期性变化. 因此，教师可在课堂中展示数学的和谐美，以增强学生的关注度，达到激发求知欲的效果.

案例1  “中心对称图形”的教学.

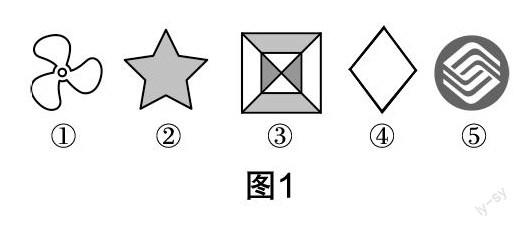
进入新课之前，教师首先带领学生回顾中心对称与对称中心的定义. 学生热身完毕后教师展示图1，要求学生观察图形并思考.

师：观察图1，说说各图形的共同点.

生1：这几张图片都具备旋转对称图形的特征.

师：不错！旋转对称是它们的共同之处，你们还能找出它们的不同之处吗？

生2：旋转的度数不一样.

师：那它们旋转的角度分别为多少呢？

生3：图1中①所示的图形的旋转角是120°或240°;图1中②所示的图形的旋转角可能是72°，144°，216°，288°;图1中③④⑤所示的图形的旋转角均为180°.

师：非常好！你们还有其他发现吗？

生4：图1中②③所示的图形都是轴对称图形，图1中③④⑤所示的图形需要旋转180°之后才能与它本身重合.

师：太棒了！这些图形带给你们什么感觉？

生（齐）：赏心悦目的感觉.

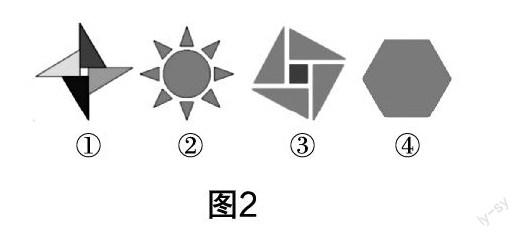
师：这就是数学的和谐美、对称美. 今天我们来学习一个新的知识点“中心对称图形”. 在课前预习中，大家已经初步接触过该部分知识，现在请大家观察图2，说说这些图形是否符合中心对称图形的特征，假如符合，找出其对称中心.

在学生顺利完成此问后，教师又展示了26个英文字母的大写正体图（如图3所示），让学生找一找图中有哪些字母符合中心对称图形的特征.

[图3][A B C D E F G H I J K L M

N O P Q R S T U V W X Y Z]

随着各组图形的展示，学生在回顾旧知与学习新知中逐渐加深了对“中心对称图形”的理解程度. 這些图形的展示可直接刺激学生的视觉感官系统，让学生体会并欣赏到数学独特的美. 尤其是图3的展示，不仅激发了学生的探究欲，还让学生深刻体会到数学知识在生活实际中的应用，有效地推动了学生继续深究的欲望.

除此之外，教师还可利用多媒体展示一些举世闻名的建筑，如埃菲尔铁塔、长城、泰姬陵等，让学生从这些充满艺术感的宏伟建筑中感知数学举世无双的美.

探究简洁美，启发数学思想

爱因斯坦认为：简洁是美的本质. 数学既具有简单、朴实之感，又有深厚底蕴之基，因此它具有至高无上的美. 欧拉公式eix=cosx+isinx堪称世界上的完美公式，其作为简洁美的代言人，寥寥几个字母囊括了数学深奥的内涵.

同样，我们耳熟能详的圆的面积与周长公式：S=πr2，C=2πr，都以简单明了的数字和字母表达了内涵丰富的数学知识. 类似于这样的公式、定理很多，可见简洁美对探究数学内涵，启发学生的数学思想具有深远的影响.

案例2  “勾股定理”的教学.

教师分别呈现两组勾股数组.

第一组：3，4，5;5，12，13;7，24，25;9，40，41;…

第二组：6，8，10;8，15，17;10，24，

26;…

要求学生分别观察这两组数据，分析组成每组勾股数的三个数之间具有怎样的规律.

学生在观察、交流、比较与总结后发现如下规律：第一组数据中32=4+5，52=12+13，72=24+25…即最小边为奇数的一组勾股数中，最小边的平方与其他两个连续正整数的和是相等的. 由特殊到一般的数学思想可进行以下推导：因为（2n+1）2=4n2+4n+1=2（2n2+2n）+1，所以（2n+1）2+（2n2+2n）2=（2n2+2n+1）2，其中n是正整数.

第二组数据中6，8，10可理解为62=2×（8+10），依次有82=2×（15+17），102=2×（24+26）… 从特殊到一般来推导可得（2n）2=2[（n2-1）+（n2+1）]，所以（2n）2+（n2-1）2=（n2+1）2（n≥2，且n为正整数）.

根据这两个规律，学生很快就写出了许多组类似的勾股数组. 整个教学过程轻松、和谐，学生在数学独有的简洁美与规律美中体验数学思想，培养数感，提升数学素养.

感知抽象美，启发数学思维

抽象性是数学的主要特征之一. 数学的抽象美一般指用概念、定义、公式等表达自然现象或规律等. 教学中，我们常从贴近学生生活经验的事物入手，帮助学生发现数学的抽象美. 同时，它还体现在一些抽象的量脱离具体事物后可代表特殊的量，也可作为任何具体的数，但又不等同于具体的数.

例如我们所熟悉的“N”，它可以是英文字母，也可以代表N个数，或N张纸等，它具体代表的是1或10还是100，并没有一个定论. 这就是数学抽象美的体现，带给我们无限可能与希望.

案例3  “有理数乘方”的教学.

这是学生刚步入初中阶段所接触到的知识，此时学生仍以直观形象的思维为主，教师若想依靠讲授知识的方式教学，很难达到预期教学目标. 因此，笔者结合了信息技术、联想类比思想、设疑法与发现教学法等手段，通过逐层渗透的方式让学生体会到数学的抽象美，以启发学生的数学思维，达成教学目标.

师：大家玩过算24点的游戏吗？

生（齐）：玩过，就是随机出四张牌，把每张牌面数据都用一次，计算出24的结果.

师：非常好！今天我们的规则是黑色牌面为负数，红色牌面为正数，现在请大家看电子白板，上面显示着黑桃3、红桃3、方片5、梅花4，你们能以这一组数字算出24吗？

生1：可以，-3×（-4）=12，5-3=2，2×12=24.

师：不错！若呈现的四张牌面都是3，能算出来吗？

生2：-3-[3×3×（-3）]=24.

师：若少一张黑桃3，就剩三张3，能否算出24呢？

学生窃窃私语，一时想不出答案. 此时，教师提示大家进行组内交流，尝试换一个角度去思考.

生3：我们组讨论出-3+33=24.

其他学生自主给予这个小组热烈的掌声，对他们的结论表示认同与鼓励.

教师趁机以33为线索，引出乘方就是乘法运算的定义，并自然导入新课“有理数的乘方”，学生的数学思维在计算24点的活动中得到启发. 接下来就是运用数学的抽象美进行实践活动，以拓展学生的思维.

师：请大家折叠手中的A4纸，并记录每折叠一次，纸张的层数.

学生动手操作并记录：对折一次，2层;对折两次，4层;对折三次，8层;对折四次，16层……

师：若不断地对折，层数变化呈现怎样的规律性？

生4：每次都是前一次的两倍.

师：若现在对折了20次，你们能计算出有多少层吗？

生5：按照以上规律，应该就是用20个2进行相乘的得数.

师：怎么表示更方便呢？

生6：2個2相乘是22，3个2相乘是23，4个2相乘是24，那么20个2相乘应该是220.

师：若折叠了n次，怎么写？

生7：2n.

师：若现在不是n个2相乘，是n个a相乘，[][]，我们可以怎么简写？

生8：是不是可以记作an？

师：太棒了！求若干个相同因素相乘的积，我们称它为乘方，它的结果为幂. 如图4所示，a是用来相乘的相同因数，我们称它为底数，n是指几个因素相乘，称为指数.

数学的抽象美是人类智慧的体现，如我们常用的阿拉伯数字，区区十个符号就为我们创造出一个无限宽广的数学世界;再如几条直线加几个蝌蚪样的音符，就创造出美妙的音乐等，这些都是人类创造的抽象美.

总之，数学美存在于社会与生活的方方面面. 教师在教学中，应充分利用数学美来陶冶学生的情操，启发学生的思维，让学生在美的感知与体验中获得深刻感悟，从而提高教学质量，提升学生的数学核心素养.