促进高层次理解 强化统计学意义

仲秋月

一、凭借直觉体验，感受代表性

【教学片段1】

1. 课前活动。

教师组织男女生代表玩套圈游戏。

学生议一议：怎样做到游戏公平？

2. 情境创设。

师：数学可以帮助我们解决很多实际问题。

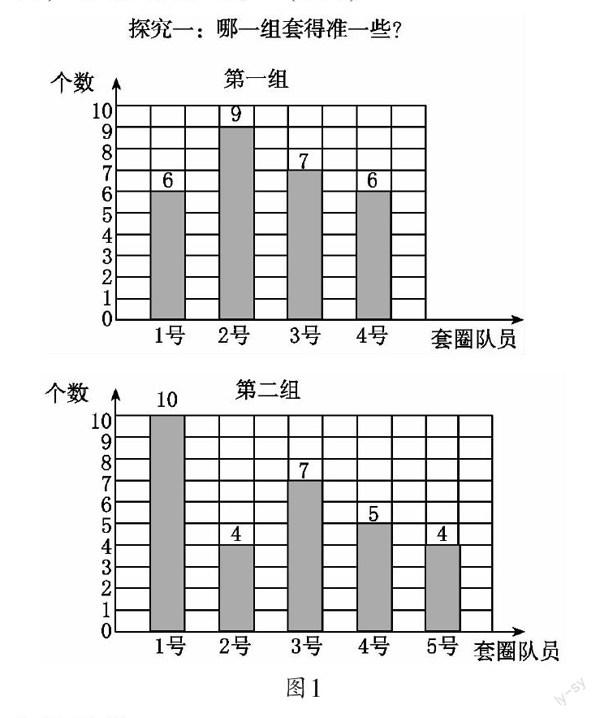
出示情境图：四个小组进行套圈比赛，每人套15个。哪一组套得准些？（图略）

师：老师用条形统计图表示出第一组和第二组的套圈情况，你能看懂吗？（图1）

3. 交流思辨。

师：第一组和第二组比，哪一组套得准些？你是怎么想的？

生：第二组，因为第二组中的1号队员套中了10个！

师：真厉害，我宣布第二组获胜！

生：我不同意，虽然1号队员套了10个，但是其他队员都套得比较少。

师：1号队员能代表第二组的水平吗？

师：看来，套中10个或者套中4个，这些成绩都只能代表某个队员的水平，不能代表这一组的整体水平。那该怎么办？

生：把第一组、第二组套中的总和算出来比一比。

师：第一组总成绩是28个，第二组总成绩是30个，能比出结果了吧？

生：我不同意，第二小组多了一个队员，假如再加上一个队员，总数还会更多，比总数不公平！

4. 自主探究。

师：选其中一个队员的成绩比不行，比总数也不行，看来这个比较整体水平的代表数需要我们自己来创造。哪个数能代表第一组的整体水平呢？哪个数能代表第二组的整体水平呢？小组讨论，把想法记录在学习单“探究一”中。

师：请问你找到了哪个数代表第一组的成绩呢？

生：我找的数是“7”。（图略）

师：你们能看懂他图上画的两个箭头吗？

生：他的意思是把2号同学套中的9个里面拿一个给1号，再拿一个给4号。

师：为什么要给1号和4号呢？

生：因为他们套中的比较少。

师（演示移动过程）：这时候4个队员套中的个数变得怎样？

师：用“7”这个数代表第一组的整体水平，可以吗？你们有没有其他意见？

揭示：“7”就是这组数据的平均数。

【赏析】平均数作为统计量，其意义在于刻画、代表一组数据的整体水平。平均数不同于原始数据中的每一个数据（可能碰巧与某个数据相等），但又与每一个原始数据相关，代表这组数据的平均水平。要对两组数据的总体水平进行比较，就可以比较这两组数据的平均数，因为平均数具有良好的代表性，不仅便于比较，而且公平。刘老师创设了学生感兴趣的游戏情境，选择两组精心设计的数据，通过动态呈现和思辨追问，激发学生的认知冲突，使学生直观体验到每一个数据都难以代表整体水平，必须创造一个“新数”。

二、通过问题引领，理解虚拟性

【教学片段2】

1. 对话交流。

師：巧了，3号队员的成绩就是7个，这两个“7”一样吗？

生：不一样，平均数“7”代表的是第一组的整体水平，3号队员的“7”只代表他自己一个人的成绩。

2. 独立探究，深化认知。

学生独立探究第二组的平均数。

师：我们找到了第二组的平均数“6”，可是第二组没有哪个队员投6个呀？

生：“6”是平均数，并不是哪个队员投中的个数。

师：“6”是哪几个数的平均数？

生：“6”是“10、4、7、5、4”这5个数的平均数。

生：平均数“6”原来是没有的，是我们通过移多补少得到的。

师：平均数“6”能代表1号队员的成绩吗？能代表2号队员的成绩吗？它究竟代表的是哪个同学的成绩呢？

生：代表的是第二组所有同学的成绩。

生：代表了这一组的整体水平。

生：“6”不是原来5个数中的任何一个数，只是代表这些数的数。

师：明白了，平均数并不是原来数据中的哪一个，而是我们创造出来的、代表整体水平的数。有时可能碰巧会和原来数据中的某一个相等，也可能和原来数据中任何一个都不相等。

【教学片段3】

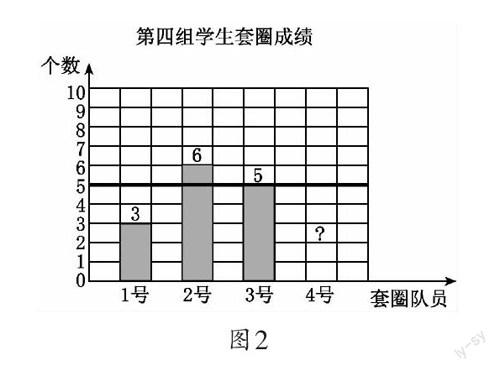
出示第四组学生套圈成绩统计图。（隐去具体数据，仅保留平均线，图略）

师：4个人的平均成绩是5个，是不是每个队员都套中5个呢？

生：不可能，因为这个“5”是平均数。

生：有可能其中有队员套中5个，但不会全部都套中5个。

师：有没有可能这4个队员都套中5个呢？

生：也有可能，但这种情况比较特殊。

生：有可能有人套中5个，也有的比5个多，也有的比5个少。

【赏析】平均数是在描述一组原始数据的过程中产生的，它不是客观存在的，具有虚拟性。如何让学生理解“平均数只刻画整体水平而不是真正的其中某一个数据”呢？刘老师通过层层递进的问题引领，帮助学生在描述数据、进行整体水平对比的过程中深化对“平均数是一种统计量”的本质的认知，实现从统计学的角度学习平均数，强化平均数的统计学意义。

三、巧妙设置变式，体会敏感性

【教学片段4】

1. 探究活动。

出示第三组学生套圈成绩。（各个队员的成绩为：4、5、9、5、7。图略）

引导学生自主探索“先合后分”的计算方法。

2. 设置变式。

师：第三组还有一位6号队员没有出场呢！瞧，他套中了几个？（课件出示6号队员成绩为0）

师：这一组的平均数还是“6”吗？你是怎么想的？

生：还是6，因为加起来的总数不变，还是30个。

师：总数不变，平均数也不变！

生：不对，平均数会变！

师：总数没有变，平均数怎么就变了？

生：因为人数变了，多了6号队员，所以我们计算的时候要总数除以6！

师：增加了一名队员，怎么平均数变少了呢？

生：6号队员投中了0个，他拉低了整体水平。

师问生：现在你觉得平均数还是“6”吗？

师：每一个数据都会对整体的平均数产生影响。

【教學片段5】

1. 设疑激趣。

出示：第四组学生套圈成绩的平均数是“5”，请问4号队员套中了几个？（图2）

2. 设置变式。

师：假如4号队员投了10个，平均数还是“5”吗？

师：比画一下，现在平均数会怎样？

学生用手势表示平均数升高。

生1：现在平均数是“6”。

师：为什么会变成“6”？

生2：因为4号队员增加了4个，这4个正好平均分给一人一个，所以平均数就增加了“1”。

师：如果4号队员的成绩变少了，平均数会改变吗？

师：看来平均数很“调皮”，会随着数据的变化而发生变化。

【赏析】平均数与该组数据中的每一个数据相关，稍有风吹草动就能带来平均数的变化，这就是平均数的敏感性。这一抽象的性质如何让小学生理解呢？刘老师巧设极端数据，通过适当的、把握本质的追问，让学生进一步深化对平均数性质的认知。借助直观的条形统计图，引导学生“看着图想”或“通过计算想”，学生思维上、情感上经历了从一筹莫展到茅塞顿开的过程，对平均数的意义以及性质有了更深的体会。

四、基于真实数据，解释合理性

【教学片段6】

练习1：全国人均月收入为3683元，苏州市人均月收入为6917元。

师：你知道这两个平均数表示什么意思吗？你有什么想法吗？

练习2：评价一座城市的健康水平，不是看医院治了多少病人，做了多少手术，而是看老百姓的平均寿命和生活质量。“以健康为中心”的理念，已融入苏州市各项政策当中。2019年中国人均寿命为77.3岁，苏州市人均寿命为83.82岁，苏州市该指标处于持续向上攀升的良好态势。

师：找到平均数了吗？你有什么想法？

师：我们生活在苏州，是不是每个人的寿命都能达到83岁？

练习3：根据有关规定，铁路部门对学龄前儿童实行免票乘车，即一名成年人可以携带一名身高不足1.2米的儿童免费乘车。1.2米这个数据可能是如何得到的？据统计，目前苏州市6岁男童身高的平均值是117厘米，女童身高的平均值是116厘米。请根据上面的信息解释免票线确定的合理性。

【赏析】叙述出概念的定义，或者会计算，不等于真正理解某个概念，还要看能否在不同情境中运用概念。由于平均数这个概念对小学生而言是非常抽象的，平均数的背景也很复杂，如果学生能在稍复杂的背景下运用平均数的概念解决问题，说明学生初步理解了平均数。因此，刘老师给出了三组复杂程度不同的真实数据，引导学生借助前面所学的平均数的意义和性质来解释这些数据，体会其合理性，知道什么情况下用平均数做判断、做预测的结论更好，在真实问题情境中加深对平均数作为一个统计量的意义与价值的理解。

（作者单位：江苏省苏州工业园区东延路实验学校责任编辑：王彬）