放手让学生自选条件计算圆柱的表面积

明启文

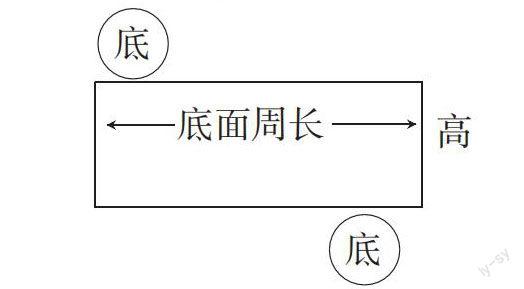
圆柱的展开图是一个组合图形，计算圆柱的表面积实际就是计算这个组合图形的面积，组合图形的面积学生会计算，因此，教学时可以放手让学生自选条件计算圆柱的表面积;课本上第22页的例4可以让学生自学理解;练习题也让学生独立审题，找出解题须理解和突破的小障碍，这样，课堂上学生积极地进行思维，主动地参与学习，收获会更大。

教学开始，由复习逐渐引入新课。师：上节课我们学习了圆柱的认识，你们能不能画出圆柱的展开图？（能！）请你们在草稿本上画出来，并标出各部分的名称。全班在草稿上画，抽生上黑板上画，改正后得到：

师：今天我们学习“圆柱的表面积”（板书），圆柱的表面积指的是哪部分的面积？（生：就是展开图中一个长方形和两个完全相等的圆的组合图形）

师：组合图形的面积你们会算吗？（会！）

师：假如在这个组合图形中，我只告诉你两个最基本的条件，让你计算圆柱的表面积，你需要哪两个条件？

学生经过思考后，有人提出：我需要底面半径和圆柱的高;有人提出：我需要底面的直径和圆柱的高;还有人提出：我需要底面周长和圆柱的高。接着老师布置练习：需要底面半径和圆柱的高的做第23页练习四第6题的第3图（r=5cm，h=12cm）;需要底面直径和圆柱的高做第23页练习四第1题的第3图（d=18cm，h=15cm）;需要底面周长和圆柱的高的做这个：C=6.28dm，h=7dm。学生开始根据给定的条件进行计算，每个人必须选择其中的两种情况进行解答。（要求分步解答）

抽生到黑板上解答，并讲解，这样便依次得到：

a：已知r=5cm，h=12cm。

①先算两个底面的面积：2πr2=2×3.14×52=157（cm2）;

②求底面周长：2πr=2×3.14×5=31.4（cm）;

③求这个长方形的面积（圆柱的侧面积）：Ch=31.4×12=376.8（cm2）;

④求圆柱的表面积：157+376.8=533.8（cm2）。

b：已知d=18cm，h=15cm。

①先求半径r=d÷2=18÷2=9（cm）;

②再求两个底面的面积：2πr2=2×3.14×92=508.68（cm2）;

③求底面周长：πd=3.14×18=56.52（cm）;

④求圆柱的侧面积：Ch=56.52×15=847.8（cm2）;

⑤求圆柱的表面积：508.68+847.8=1356.48（cm2）。

c：已知C=6.28dm，h=7dm。

①先求侧面积：Ch=6.28×7=43.96（dm2）;

②再求底面半径：=6.28÷（2×3.14）=1（dm）;

③求两个底面的面积：2×3.14×12=6.28（dm2）;

④求圆柱的表面积：43.96+6.28=50.24（dm2）。

学生的解答是正确的，讲解的层次也是清晰的。这时老师提问：在你们需要的条件中，哪一个条件是必须具备的？为什么？（经过学生的发言和讨论，可得到：圆柱的高是必须具备的条件，因为计算圆柱的侧面积时需要用圆周长和高相乘，别的条件是代替不了“高”的。到于底面积和底面周长，只要知道底面的半径、直径或周长中任意一个条件，便可推导转换得到。）师：你们觉得这3个条件，知道哪一个计算起来更容易一些？知道哪一个计算起来难一点？（学生纷纷发表看法，讨论总结为：已知底面的半径，计算起来容易一些，因为无论是计算底面的周长或者面积，都可以直接代公式;已知周长时，计算底面积时，需用r=先求出半径，这种难一点。根据学生的发言和討论，可得到如下的板书：

师：同学们可根据不同的条件，求出完整的圆柱的表面积。其实在我们生活中，有时并不需要求完整的圆柱的表面积，解题要认真分析，请大家翻开课本第22页，自学例4。（学生自学例4）

待学生学完后，提问：（1）要求做一顶厨师帽的面料要多少，实际是求什么？（生：实际是求圆柱的表面积，这个圆柱因为是帽子，所以只有一个底面。）（2）你们能不能说一说解答的步骤？（生：能。①求侧面积：3.14×20×30=1884（cm2）;②求帽顶的面积：3.14×（20÷2）2=314（cm2）;③需要多少面料：1884+314=2198≈2200（cm2）师：计算的结果是2198，是一个准确数，你是采用什么方法处理后得到一个近似数2200呢？（是用“进一法”处理的，根据实际不需要百位以下的数，所以百位以下的数学，不论大小，统统去掉，但要在百位上进一。）（3）本题的答案为什么采用“进一法”取近似数？（生：因为实际使用的面料要比计算的结果多一些）（4）你认为是多在哪里？（学生无言可对，老师用草图帮助理解：a.缝制时接头处 布料是重叠使用的;b.裁剪帽顶会出现边角废料）

练习。下面的题请先审题，读题后发表自己的意见：提醒大家解题时要注意什么？

1.课本第23页练习四第2题：“一台压路机的前轮是圆柱形，轮宽2m，直径1.2m。前轮转动一周，压路的面积是多少平方米？”（生提醒：实际是求圆柱的侧面积，不包括两个底面）

2.课本第23页练习四第3题：“修建一个圆柱形沼气池，底面直径是3m，深2m。在池的侧面与下底面抹上水泥。抹水泥部分的面积是多少平方米？”（生提醒：实际上是求圆柱的表面积，但只有一个底面）

3.课本第24页练习四第8题：“王阿姨做了一个圆柱形的抱枕，长80cm，底面直径18cm。如果侧面用花布，底面用黄色的布，两种布各需要多少？”（生提醒：此抱枕是一个完整的圆柱，计算所用的布料，是求表面积，但所提的问题是：“两种布各需要多少？”因此，两个底面的面积和侧面积分开计算后，不要相加，要分开回答。计算结果要采用“进一法”处理）

4.课本第24页练习第13题：“一根圆柱形木料的底面半径是0.3m，长是2m。如下图所示，将它截成4段，这些木料的表面积比原木料增加了多少平方米？”

（生提醒：从图上看截成4段，实际上是截（锯）了3次，每锯一次就增加两个底面，锯了3次就增加了6个底面的面积。题中的“长是2m”与解题无关，是多余条件）

经过学生的讨论提醒后，然后让学生解答练习。