利用图像巧解高考数列题
2022-05-30黄亚男刘英丽高寿兰
黄亚男,刘英丽,高寿兰
(1.上海师范大学 数理学院,上海 200033;2.湖州师范学院 理学院,浙江 湖州 313000)
1 例题解析
例1(2021年上海秋季高考第12题) 已知ai∈*(i=1,2,…,9),对任意k∈*(2≤k≤8),ak=ak-1+1或ak=ak+1-1有且仅有一个成立,且a1=6,a9=9,则a1+a2+…+a9的最小值为______.
分析本题的题干内容简短,对一组9项数列进行限制,从第2项开始,每一项或前一项加1,或后一项减1,这两种情况有且只有一个成立,求这9项和的最小值.
解由于该9项数列的首项a1=6和末项a9=9已知,因此可以分别从首项a1和末项a9开始考虑.
情形1从a1开始考虑,接着确定a2的值.因为要求数列和为最小值,所以每一项应尽量取最小,若a2取最小的可能值1,则可排除前一项加1的情况,只能是后一项减1,继而可以求得a3=2,依次类推直到最后一项.由此可以列出以下式子:
a2=a1+1( )或a2=a3-1(√),
a3=a2+1(√)或a3=a4-1( ),
a4=a3+1( )或a4=a5-1(√),
a5=a4+1(√)或a5=a6-1( ),
a6=a5+1( )或a6=a7-1(√),
a7=a6+1(√)或a7=a8-1( ),
a8=a7+1( )或a8=a9-1(√).
在这种情况下,得到的数列为:
a1=6,a2=1,a3=2,a4=1,a5=2,a6=1,a7=2,a8=8,a9=9.
因此,a1+a2+…+a9=32.
情形2从a9=9开始考虑,接着确定a8的值.若a8取最小的可能值1,那么a8只能是前一项加1的情况,则a7=0,这不符合题意.所以a8只能先取值到2,依次往前类推直到a2.由此可以列出以下式子:
a2=a1+1(√)或a2=a3-1( ),
a3=a2+1( )或a3=a4-1(√),
a4=a3+1(√)或a4=a5-1( ),
a5=a4+1( )或a5=a6-1(√),
a6=a5+1(√)或a6=a7-1( ),
a7=a6+1( )或a7=a8-1(√),
a8=a7+1(√)或a8=a9-1( ).
在这种情况下,得到的数列为:
a1=6,a2=7,a3=1,a4=2,a5=1,a6=2,a7=1,a8=2,a9=9.
因此,a1+a2+…+a9=31.
通过讨论以上两种情形,可得a1+a2+…+a9的最小值为31.
以上是一种纯代数的解题方法,即根据题目给出的条件,逐步分析得出满足条件的数列,最终得到答案.然而,我们也可以利用函数的思想来理解此题,即将题目中的数列看作离散型函数,利用函数图像去观察分析,其更简洁、更直观.将题干的每一项要求反映到函数图像中,即从第二项开始,每一项或前一项升1格得到,或后一项降1格得到,这两种情况只有一个成立,即不能出现升1格再升1格和降1格再降1格的情况.下面分两种情形考虑:
第一种情形:从a1开始画图,接着确定a2的点.为使数列之和最小,尽量使每一项取值最小,所以将a2降到最小值1,则a2只能由a3降1格得到,此时a3如果满足由前一项a2升1格得到的情况,就不能满足后一项a4降1格得到a3的情况,继而a3只能降1格得到a4,依次类推直到a7=2.若a7由a6升1格得到,则a7不能再升1格得到a8,那么a8只能由a9降1格得到,即a8=a9-1=8,结果如图1所示.
在这种情况下,得到的数列为:
a1=6,a2=1,a3=2,a4=1,a5=2,a6=1,a7=2,a8=8,a9=9.
因此,a1+a2+…+a9=32.
第二种情形:从a9=9开始考虑,接着确定a8的点.若a8直接降到最小值1,则a8只能由a7升1格得到,a7=a8-1=0,这不符合题意,所以a8只能先降到2.为满足题意,a8只能满足由前一项a7升1格得到的情况,依次类推直到a3=1.若a3由a4降1格得到,则a3不能再降1格得到a2,则a2只能由a1升1格得到,即a2=a1+1=7,结果如图2所示.

图1 正向讨论数列ai∈*(i=1,2,…,9)的各项值Fig.1 Forward discussion of the values of the sequence ai∈*(i=1,2,…,9)
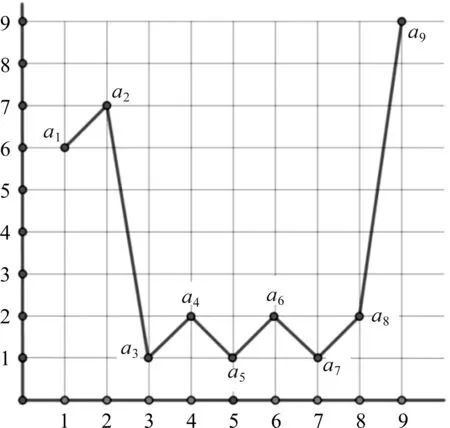
图2 逆向讨论数列ai∈*(i=1,2,…,9)的各项值Fig.2 Inverse discussion of the values of the sequence ai∈*(i=1,2,…,9)
在这种情况下,得到的数列为:
a1=6,a2=7,a3=1,a4=2,a5=1,a6=2,a7=1,a8=2,a9=9.
因此,a1+a2+…+a9=31.
通过讨论以上两种情况,可得a1+a2+…+a9的最小值为31.
为方便讨论2021年上海秋考第16题的解法,本文首先给出关于开口向下的二次函数的1个性质.
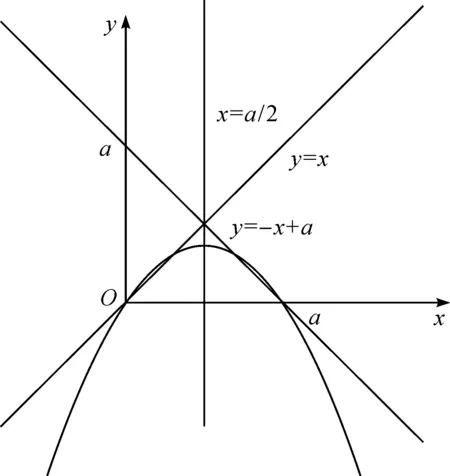
性质1设f(x)是开口向下的二次函数,如果在f(x)的一个单调递增区间内有3个数x1 2f(x2)=f(x1)+f(x3), 则有2x2 证明设二次函数f(x)=a(x-t)2+k,其中a<0.在单调递增区间(-∞,t)上,任取x1 由 可得: 即 注设f(x)是开口向下的二次函数,如果在f(x)的一个单调递减区间内有3个数x1 例2(2021年上海秋季高考第16题) 已知实数x1、y1、x2、y2、x3、y3同时满足: (1)x1 则下列选项中恒成立的是( ). 分析本题对6个实数x1、y1、x2、y2、x3、y3加以限制,即要满足题干的3项要求,以此来判断x1、x2、x3之间的关系.由于这是一道选择题,我们可通过猜测直接选出答案.但在实际的猜解过程中发现,这并不容易,因此我们可以从函数的角度理解题意.通过观察可以发现,这6个实数可以按(x,y)分为3组,即(xi,yi),i=1,2,3,将每一组(xi,yi)分别看作一个点,记这个点为Pi.将题干的每个条件转化到图像中,以更加直观地理解. 将条件(1)转化到图像中去理解,即点Pi(i=1,2,3)均在直线y=x上方. 将条件(2)转化到图像中去理解,即点Pi(i=1,2,3)的横坐标与纵坐标之和是一个定值,记作a,a∈.于是,点Pi(i=1,2,3)落在直线y=-x+a上. 图3 运用数形结合构建已知条件函数图像Fig.3 Constructing the function images of the known conditions by using symbolic-graphic combination 解设Pi(xi,yi),i=1,2,3,由条件(1)和条件(2)可知,点Pi(i=1,2,3)落在直线y=-x+a上(a∈),且在直线y=x的上方,易得由条件(3)可得,构成一个等差数列.令f(x)=-x2+ax,则f(x1)、f(x2)、f(x3)是等差数列,由于开口向下的二次函数f(x)=-x2+ax在区间上单调递增,根据性质1知,2x2 下面举例说明选项C与选项D不一定成立. 分析本题通过函数求解得到一组无限数列x1,x2,x3,…,xn,…,求当n趋近于正无穷时xn+1-xn的值.如果用纯代数方法,分别求出各区间内满足条件的解,再求极限,这并非易事.下面采用数形结合的方法来理解题意:首先根据f(x)为奇函数和关于x=1对称这两个条件画出f(x)的图像,易得f(x)是一个周期为4的函数,x=2n(n∈)为其渐近线,再找到f(x)图像与y=x+1图像在第一象限的交点,这些交点的横坐标正是方程f(x)=x+1的正数解所构成的数列.通过图像发现,要求的极限即为正无穷处两条渐近线之间的距离. 解因为f(x)为奇函数,且关于直线x=1对称,当x∈(0,1]时,f(x)=ln(x),则f(x)是周期为4的函数,x=2n(n∈)为其渐近线,如图4所示. 图4 周期函数f(x)的图像Fig.4 Image of the periodic function f(x) 2021年上海秋季高考的第12题和第16题,以及2022年上海春季高考的第12题都是关于数列的综合应用题.本文从这3道题出发,将纯代数思想解题与函数思想解题进行比较,发现数形结合思想在处理有关数列综合题时非常有效[7].函数图像可以更简洁、更直观地反映数列每一项之间的关系,对解题具有很大的帮助.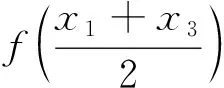

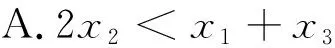
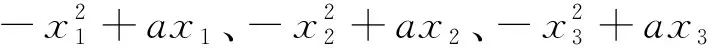
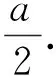



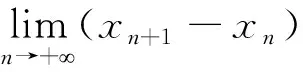
2 思考与总结
