极端海况下不同锚系形式对漂浮式海上平台的动力响应影响研究

路 宽， 王花梅， 宋雨泽， 饶 翔

(国家海洋技术中心，天津 300112)

近年来，海上平台除了应用在传统的海上油气开采领域外，也在其他新兴领域进行广泛的应用，如海洋能发电、海洋牧场、海上试验、海洋军事等等。唐友刚等[1]对浮式生产储油卸油装置(floating production storage and offloading, FPSO)与水下软刚臂及锚缆多体进行了耦合水动力分析，丁勤卫等[2-3]对海上漂浮式风机的水动力进行了分析研究，凌宏杰等[4]针对近岛礁浮式平台运动响应特性进行了研究，还有针对深水浮式海洋平台[5]、多浮体海上平台[6]、半潜式平台[7]等新兴应用领域的海上平台的水动力开展了深入的研究工作。与传统海洋平台相比，此类平台多采用半潜式、立柱式或张力腿式，工程造价较低，结构简单，应用方便。但同时，由于此类平台为了满足应用需求，往往选择布放在海况恶劣的海域，如海上试验平台需要典型或极端海洋环境数据进行比测试验，海洋能发电平台也需要布放在海上风能、波浪能或潮流能资源集中的海域，这就对海上平台的设计提出了更高的要求。通常情况下，此类平台在设计海况下的安全性是具有保障的，然而在实际运行中，由于台风等极端海况频发，超设计海况的发生概率呈增加趋势，一旦发生超设计海况，平台随时会发生损坏，对人员和财产的安全造成严重的威胁。

位于国家海洋试验场的“国海试1”海上试验平台，为漂浮式海上试验平台，主要服务于海洋仪器设备规范化海上试验与测试工作，为我国海洋仪器科技创新与成果转化提供公共试验平台。该平台自2019年9月下水运行以来，已连续在位运行一年以上，服务了10余项科技部重点研发计划课题验收海试工作。在位运行期间，由于先后经历了2次极端海况，造成了轻微的走锚现象，为了避免出现更为严重的破坏，有必要对其锚泊系统进行维护与改造。

漂浮式海上平台的抗风浪能力很大程度上由锚泊系统决定[8-9]，特别是在极端海况下，锚泊系统的可靠性至关重要，因此有必要针对不同锚系形式下平台的动力响应进行分析与比较。目前，对于海上平台水动力特性研究的主要方法包括理论分析、数值模拟[10-11]、物理模型试验[12-15]和现场观测试验。近年来，随着超算中心与大型波浪水池的建立，数值模拟与物理模型方法成为研究此类问题最主要的手段。本文在应用威海海域实测与重现期推算数据的基础上，采用数值模拟与物理模型试验相结合的研究方法，对不同锚系下该漂浮式海上试验平台在极端海况下的运动响应进行了分析与比较，研究结果为锚泊系统的改造提供了依据。

1 威海海域情况与锚系方案

“国海试1”海上试验平台布放于山东省威海市褚岛北部海域，该海域海底地形起伏较大，岛北部近岸水下形成一条海沟，成东西向分布，最大水深约70 m，平台如图1所示。

图1 “国海试1”海上试验平台Fig.1 National Sea Trial 1 platform

根据2019年海域实测资料统计，全年平均风速4.1 m/s，风速大于8 m/s的频率为8.3%。2013年和2015年，国家海洋技术中心通过多参数综合浮标搭载的波浪传感器对海域进行了全年的波浪观测，并采用ADCP对平台布放点位进行了大小潮的观测。根据现场观测数据，对海域不同重现期的风、浪和流进行了推算，结果如表1所示。

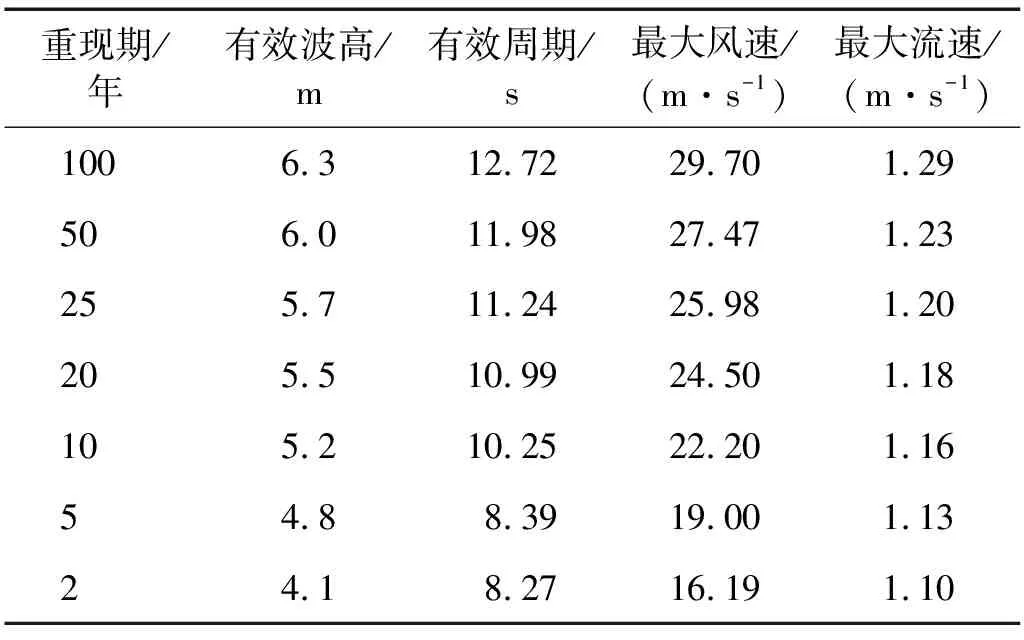
表1 平台所在海域风浪流重现期推算结果Tab.1 Extreme sea area condition of the platform

当前平台的锚泊系统采用的是拉紧的V型链方式，锚链为长度为82.5 m，直径32 mm的AM2龙须链，锚块采用2 100 kg的AC-14大抓力锚。改进后的锚泊系统考虑采用倒S松弛式，即浮筒与趟地链相结合的方式，在V型链末端增加浮筒，同时连接锚块的主链由55 m增加到165 m。

2 数值模拟

2.1 模拟方法

利用ANSYS AQWA模块，对平台原型进行数值模拟计算，平台的数值模型与建立的坐标系，如图2所示。

图2 海上试验平台数值模型Fig.2 Numerical model of platform

平台全局采用结构化网格划分，在棱角处与月池的部分用非结构化网格进行处理。计算时，风浪流外荷载取值见表1，方向为威海海域极端波浪方向，即x方向。其他主要的环境参数与尺寸，如表2所示。

对两种不同锚系形式分别进行了数值计算，原方案为拉紧的V型链方式，锚链参数如前所述。改进之后的方案，锚定点位置不变，将同一侧的连接点至锚定点的系泊缆长度增加至137.5 m，形成“松弛式”的系泊形式。

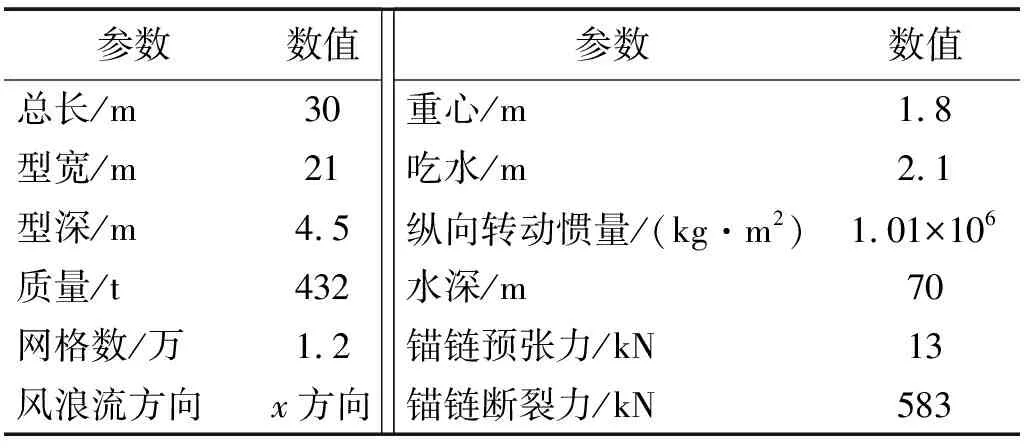
表2 主要计算参数Tab.2 Main calculation parameters

考虑到波浪是主要外荷载，而波浪对于平台的作用力中流体黏性的影响相对较小，对运动和载荷的计算可以忽略，因此采用三维势流理论进行水动力计算，即假设流体式不可压缩、无黏性和无旋的。同时对时间项采用频域和时域两种计算方法，并考虑辐射阻尼的作用，对平台水动力系数和运动响应继续数值计算分析。控制方程如式(1)所示

(1)

式(1)为拉普拉斯方程，可应用速度势φ，来表达流场内的流体速度分布

(2)

边界条件应满足

(3)

(4)

在水中平台所受到的波浪力和力矩为

F=-∬S(p·n)dS=Fr+Fw+Fd+Fs

(5)

M=-∬Sp·(r×n)dS=Mr+Mw+Md+Ms

(6)

式中：Fr，Mr为平台强迫运动产生的辐射荷载；Fw，Mw为平台固定时入射波产生的荷载；Fd，Md为平台固定时产生的绕射荷载；Fs，Ms为静水荷载；S为湿面积；p为压力。

风荷载主要作用在平台的水面以上的部分，以水平分量为主，垂直分量可忽略不计，其大小为

(7)

式中：ρa为空气密度；Uw为风速；Ch，Cs分别为平台体受风构件的高度系数和形状系数，其中由于平台在海面上高度低于15.3 m，故高度系数取1.0。形状系数吃水线以上取1.0，船舱取1.5，An为受风面积。

流荷载作用于平台的水下部分，其大小为

(8)

式中：CD为拖曳系数，此处取1.0；ρs为海水密度；Ac为迎流面积；Uc为流速。

实际海况下，主要的环境荷载为波浪、潮流与风的耦合作用为主要荷载，分析耦合荷载作用时需要从频域和时域两个方面考虑。在频域分析中，以波浪频率ω为研究变量，平台在海上除了收到风、浪、流影响之外，还包括了自身运动偏离平衡位置产生的静水回复力，与运动时受到的波浪入射和绕射的作用力，其一阶频域方程为

(9)

式中：Xj为平台在j方向的位移运动；M为质量矩阵；Ma为附加质量矩阵；C为辐射阻尼矩阵；K为回复力矩阵；F为一阶波浪力矩阵。

在入射荷载仅考虑一阶项时，问题即简化为线性求解，在频域分析求解十分方便，但本文考虑入射荷载不能忽略二阶项，因此需要利用时域分析方法，将非线性项纳入方程求解。根据傅里叶变换，式(9)转换为时域运动方程

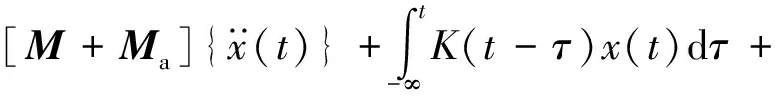
(10)

式中：K(t-τ)为延迟函数；F(t)为作用在平台的波浪力，包括一阶和二阶波浪荷载。

2.2 计算结果

由于附加质量与辐射阻尼对计算结果具有很大的影响，因此首先对平台进行频域计算，以获得附加质量与辐射阻尼系数。平台的纵摇运动的附加质量和辐射阻尼，如图3所示。

图3 纵摇附加质量与辐射阻尼Fig.3 Added mass and radiation damping of pitching

采用时域模块对两种不同锚泊形式的百年、五十年、二十五年、二十年、十年、五年和两年一遇重现期的风浪流作用下，平台姿态与锚链受力情况进行了计算。选择最具代表性的百年一遇结果进行作图比较与分析，两种锚系形式下，平台的纵摇、横荡与锚链拉力的计算结果，如图4～图6所示。

从图4的计算结果可看出，张紧式锚系形式下平台的纵摇运动明显小于松弛式的锚系形式，前者最大与平均纵摇角分别为16°和3.5°，后者最大与平均纵摇角分别17.5°和6.1°，这说明，张紧式锚系形式在极端海况下稳定性更好。

图4 百年一遇重现期下两种锚系形式纵摇对比Fig.4 Pitching comparison of two types of mooring system in a-hundred-year recurrence period

从图5横荡运动的对比可以看出，两种锚系形式均在初始位置附近做往复运动，张紧式的运动范围大致为±10 m，松弛式运动范围从-30～40 m。可见，在极端海况下，拉紧的锚系形式漂浮的范围更小，更有利于定点试验。

图5 百年一遇重现期下两种锚系形式横荡对比Fig.5 Swelling comparison of two types of mooring system in a-hundred-year recurrence period

图6为两者锚链拉力的对比情况可以看出，张紧式比松弛式的拉力值整整高了一个量级，前者最大拉力达到了近5 000 kN，平均拉力为250 kN，后者最大拉力只有360 kN，平均拉力为180 kN，后者最大拉力为前者的7.2%，考虑到破断荷载为583 kN，因此张紧式锚链具有较大断裂风险。

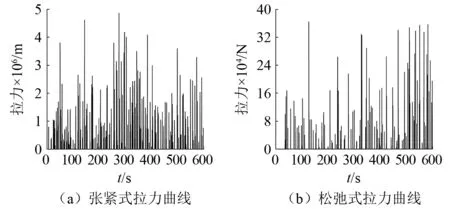
图6 百年一遇重现期下两种锚系形式拉力对比Fig.6 Force comparison of two types of mooring system in a-hundred-year recurrence period

可以看出，百年一遇风浪流重现期下，虽然拉紧的锚系形式对于平台的稳定性较好，但拉力已超出锚泊系统的承受能力，随时会出现走锚或者锚链断裂的危险；而改进后的松弛式锚系形式，虽然稳性不如前者，但抗极端海况的能力更强，安全性与生存性更高。

3 物理模型试验

3.1 试验系统及布局

为了验证数值计算的准确性，开展了模型试验，试验在自然资源部国家海洋技术中心动力环境实验室中进行，主要试验设施及设备包括：

(1) 多功能水池——长130 m，宽18 m，池深6 m，试验水深4.5 m；

(2) 造波机——10单元伺服电机驱动式推板造波机，最大波高0.6 m，周期范围为0.5～5 s，由上位机软件控制，可模拟产生规则波和不同谱型的不规则波；

(3) 造风系统——16单元轴流风机组成，最大风速10 m/s；

(4) 双线性型BG-II/1000MM波高传感器——量程0～1 m，精度0.2%；

(5) Testo热敏风速仪405i——量程0～30 m/s，精度±0.1 m/s+5%；

(6) AML_DDEN水下拉力传感器——量程250 N，精度0.1%；

(7) 六自由度非接触姿态测量系统——三光学镜头组成，量程6 m×6 m，摇摆角误差为±1.5°，水平位移误差为1.5 mm，垂荡误差为2 mm。

按照海洋行业标准HY/T 0299—2020《海洋观测仪器设备室内动力环境模型试验方法总则》规定搭建试验环境并开始试验。试验系统包括：试验环境模拟装置、平台模型与测量采集系统。其中，试验环境模拟装置包括造波机、造风机与等效水流力模拟装置。平台模型包括平台主体及其锚泊系统，锚泊系统可进行更换。测量采集系统包括：波高仪、风速仪、六自由度姿态仪及拉力传感器。各测量传感器集成在数据采集系统中，保持数据的实时性与同步性。

平台模型布放在距造波机40 m，距造风机20 m处，波高仪与风速仪布放在模型前5 m处，水下拉力传感器安装在锚泊系统与锚块连接部位，六自由非接触姿态测量系统布置在模型背浪一侧的斜上方距离5 m附近，安装由滑轮、拉力线与砝码组成的水流力模拟装置，拉力点与模型重心保持水平。试验布局如图7所示。试验前需在模型上安装标志点，以满足姿态测量需要。试验仪器均在计量有效期内，试验前也均进行了标定。

图7 试验布局Fig.7 Test layout

3.2 模型及相似准则

根据实验室试验能力与平台原型尺寸，确定模型比尺为1∶30，模型主要参数如表3所示。设计时首先考虑满足几何相似，除几何相似外，模型还满足了惯性矩和自摇周期相似，并且满足重力相似；其两种锚系结构的组成，除满足长度等几何相似外，还满足了质量和弹性相似。由于本次模型试验，水的黏滞力不是主要作用力，因此试验中并没有考虑雷诺数的影响。

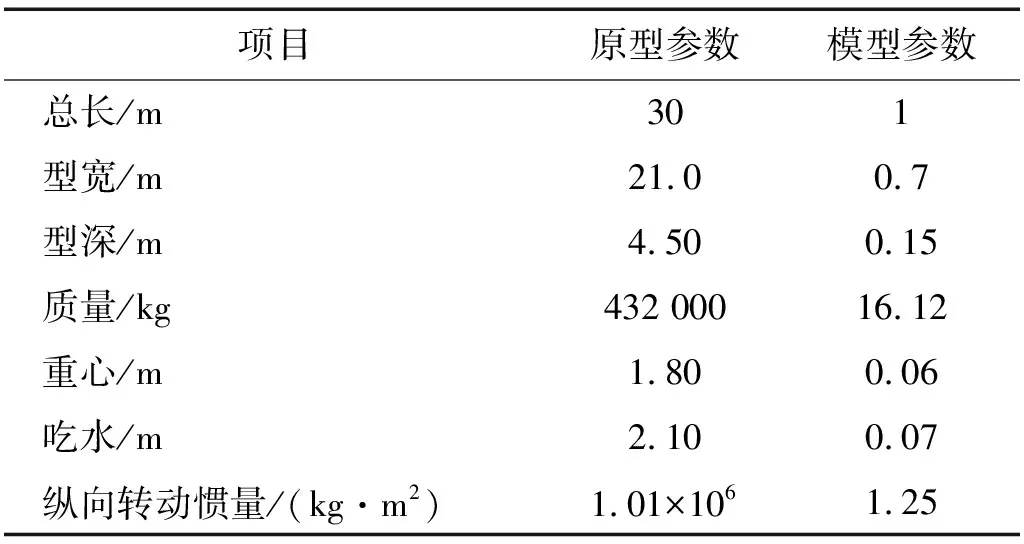
表3 模型主要参数Tab.3 Parameters of model

试验前先进行了平台模型重心与转动惯量的调节，并进行了模型及锚泊系统的整体刚度验证，模型，试验模型如图8所示。

图8 试验模型Fig.8 Test model

试验中采用两种锚系方案，如图9所示，分别为张紧式、带浮筒的倒S松弛式。张紧式锚泊系统由V型链-万向节-主链-锚块组成，松弛式由V型链-万向节-浮筒-弹簧-主链-锚块组成，锚块质量为50 kg，锚链质量与尺寸与原型保持相似。

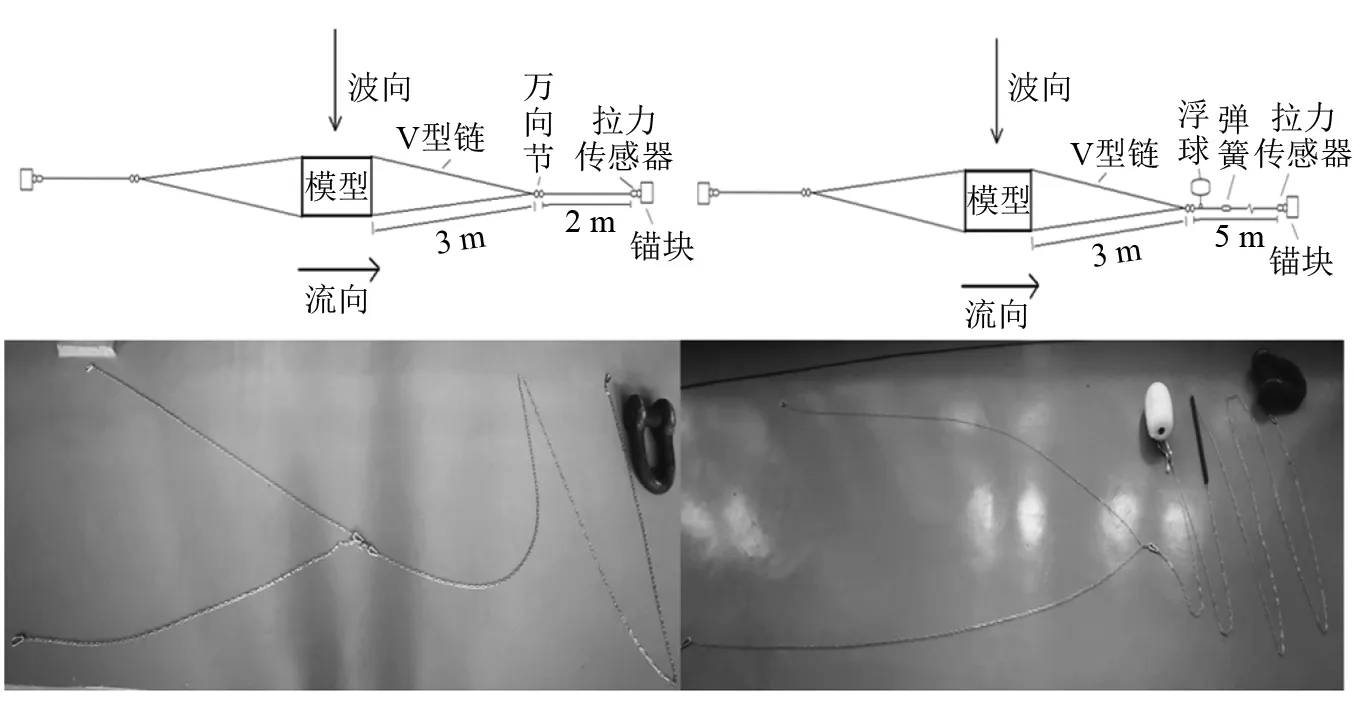
图9 两种锚泊系统方案Fig.9 Two types of mooring system

3.3 试验工况

根据原型工作海况，按照缩尺比计算，得到试验工况如表4所示，模型和原型的波浪均为深水波。两种锚系方案，每组7个试验工况，工况1～工况7分别对应原型百年、五十年、二十五年、二十年、十年、五年和两年一遇重现期。试验中，首先进行风场模拟，待风场稳定后，加载砝码模拟水流作用力，稳定后，进行不规则波的模拟。不规则波采用与实测谱对比后的JONSWAP谱，每组工况重复3次，试验时间不小于对应实船3 h。

表4 模型试验工况Tab.4 Test conditions of model

3.4 试验过程与结果分析

采用最具代表性的百年一遇试验结果，对两种锚系下模型的响应进行对比分析。风速与波浪曲线如图10所示。

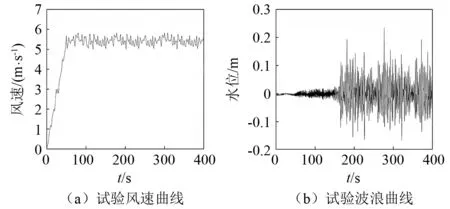
图10 试验动力环境Fig.10 Dynamic condition of test

由图10可以看出，试验开始后先进行造风，在试验进行到50 s左右，风场逐渐稳定，再加载砝码模拟水流作用力。在风的作用下，水面产生了波高约为0.04 m的小周期波浪。当模型在风和流的作用下姿态稳定后，即约150 s时，开始造浪，产生有效波高为0.21 m，有效周期为2.32 s的不规则波，上述步骤即形成风浪流耦合的极端海况。每个工况持续时间共600 s，文中统一取前400 s进行作图。

模型在上述风浪流作用下，两种锚系形式的平台横荡与纵摇、锚链拉力的对比曲线，分别如图11和图12所示。

首先分析模型的主体结构，由图11可以看出，模型在风的作用下开始进行横荡运动，在150 s附近姿态达到稳定，波浪传播到模型位置后，模型在平衡位置附近做往复运动。松弛式的平均横荡为3 m，张紧式平均横荡为1.5 m，相比而言，张紧式的漂浮范围更小，更有利于定点观测与海上试验。从纵摇摇试验结果来看，同样是在风浪联合作用下，模型做往复摇摆运动，张紧式的最大横摇角为12.5°，松弛式最大横摇角为16.7°，可见张紧式的模型主体结构稳定性更好，更有利于海洋仪器设备数据获取的准确性。

再分析模型的锚泊系统，由图12可以看出，张紧式锚链拉力显著大于松弛式，前者最大瞬时拉力达到191 N，是后者最大拉力的13倍以上。同时可以观察到，张紧式锚泊系统出现瞬时拉力的时间与出现大波的时间基本一致，即在风的作用下模型的锚泊系统处于拉紧状态，当有波浪作用在模型的时候，锚链就会出现瞬时的作用力，作用力一旦超出锚泊系统的承受范围，就会出现走锚甚至锚链断裂情况。

对全部试验数据进行了统计分析，并反演到原型的数据如表5所示。由此可以得出结论：

(1) 松弛式锚泊系统由于其锚链所受拉力较小，因此其抵抗极端环境的能力更强，维护周期更长，维护成本更低。但其平台在风浪作用下运动范围较大，因此观测与试验数据的准确度会受到一定的影响，数据应采用相关算法进行修正后方可应用。

(2) 张紧式锚泊系统的定点观测效果最好，巡航半径较小，同时，由于其在风浪作用下摇摆角更小，其试验获取的数据更为准确，但是其对锚泊系统要求较大，锚链所受瞬时拉力非常大，会出现走锚现象，特别是遇到极端海况，可能会遇到严重的损坏，为了避免事件的发生，应对锚泊系统定期进行巡检和维护，必要时采取应急避险措施。

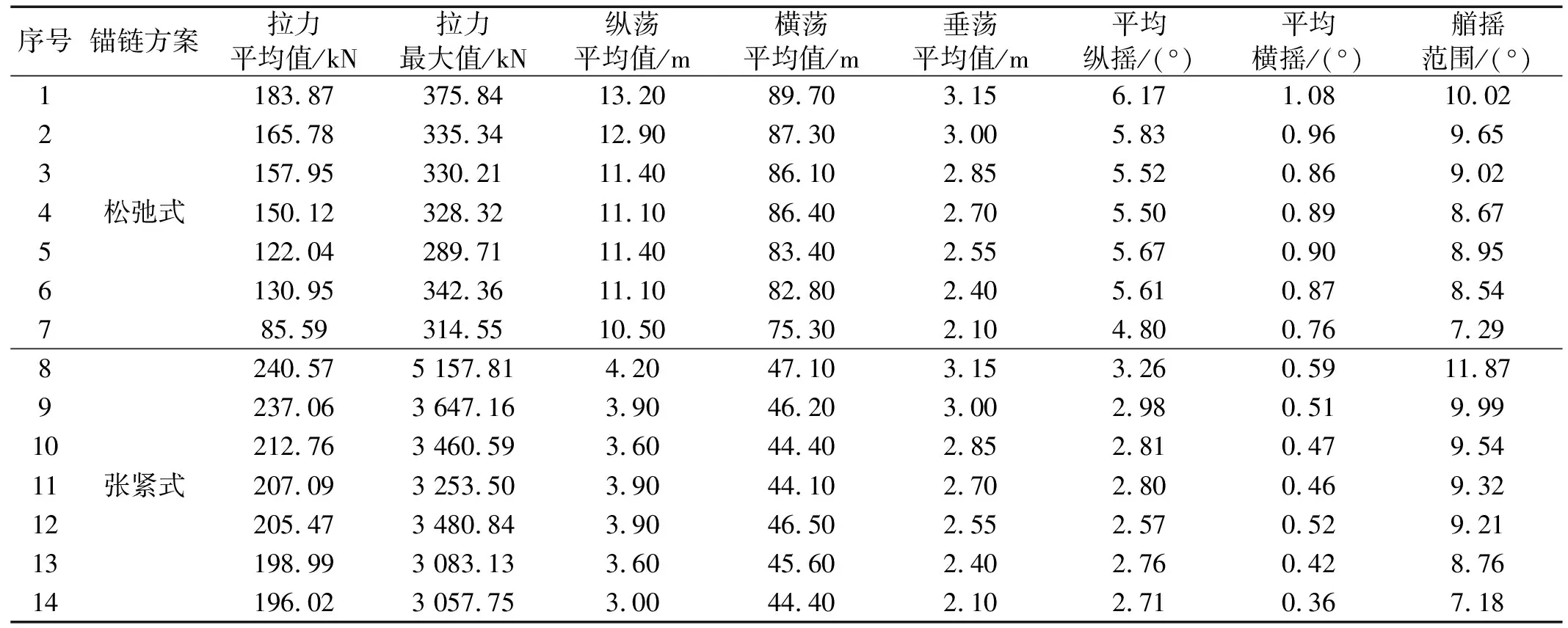
表5 原型数据统计表Tab.5 Statistical table of test data

3.5 数值模拟与模型试验的结果对比分析

通过数值模拟与物理模型试验的结果对比来看，结论是一致的，即在张紧式与松弛式两种锚系方案中，采用拉紧的锚泊系统，平台的摇荡更小，可获取到更为准确的观测数据，但是锚链所受拉力最大；松弛式的锚泊系统锚链所受拉力小，可靠性高，但是摇荡较大；如果定量来看，通过对比分析，两者数值存在大约10%左右的偏差，造成偏差的原因有以下两个方面：

(1) 试验环境产生的误差。风场质量和反射波的影响都会对试验结果造成影响；

(2) 试验过程中出现的不确定性因素。试验中，波高仪、风速仪、姿态仪、拉力计，都存在着系统误差，会对结果造成影响。

因此，通过模型试验验证后的数值模型可以应用在今后平台的水动力计算与分析工作中，对平台试验的开展、试验装置与平台的耦合计算、极端海况下平台运动预报具有重要的应用意义。

4 结 论

本文采用数值模拟与物理模型试验研究的方法，针对两种不同锚系方案，采用威海海域实测数据，对漂浮式海上试验平台在风浪流联合作用下的水动力性能进行了研究与分析，通过试验不仅定性的分析了不同方案的优缺点，而且得到了相对准确的定量分析结果，为今后类似的研究提供方法参考。最终得到如下结论：

(1) 数值模拟与物理模型试验作为平台水动力性能的主要研究手段，可以很好的预测其在复杂海况下的运动响应，而且两种方法可以相互验证，具有很好的应用前景。

(2) 威海国家海洋试验场作为国家海洋仪器装备公共试验与测试平台，需要长时间在位运行，安全性应该是首先需要考虑的因素。现有的张紧式的锚泊形式由于锚链受力较大，已超出其承受范围，因此存在一定的安全隐患。改进后的方案，即松弛式的锚系形式具有很强的抗风浪能力，在极端海况下具有较强的生存能力，更加适合平台长期在位运行。