巧用函数单调性 解题过程很轻松

安徽省灵璧县黄湾中学 华腾飞 234213

函数是高中数学的重要内容，它不但是高考重点考察的热点之一，而且它的思想方法贯串于高中数学的始终，函数的单调性又是函数的一条非常重要的性质，它的应用十分广泛.在解题的过程中，若能深入地挖掘潜在条件，恰当地构造出相应的单调函数，巧妙地运用该性质，将会起到画龙点睛的作用，起到出奇不意的效果，达到快速简捷求解的目的.下面举例说明函数的单调性在解题中的应用，目的在于使同学们对函数的单调性有更清醒的认识和更深刻的理解，并能够灵活地运用函数的单调性解决一些实际问题，提高利用函数思想解题的能力.

1 判定函数的单调区间

例1 求函数y=的单调区间.

解析：该函数是由t=-x2+2x+3 与y=复合而成的，定义域为[- 1, 3]. 因为y=是单调增函数，结合函数t=-x2+2x+3 的图像，得到函数的单调区间为[-1,1].

点评：对应复合函数，利用复合函数的单调性法则和定义域结合求解是常用的行之有效的解题方法.

例2 求 函 数y=x+(x＞0) 的 单 调区间.

解析：对于该函数，由于不可以使用复合函数单调性及单调性加减的有关性质研究，因此只能根据函数单调性的定义求解.

点评：对于特殊函数y=x+，当a＜0时，单调增区间为(-∞,0)和(0,+∞)；当a＞0时，单调区间为(-∞,)和(,+∞)，单调区间为(-,0)和(0,).应结合图像进行记忆.

例3 (2020 全国Ⅱ卷)设函数f(x) =ln| 2x+1 |-ln| 2x-1 |，则f(x) ( ).

分析：首先确定函数f(x)的定义域，并判断函数f(x)的奇偶性，然后针对选项给出的区间化简函数解析式，最后根据对数函数的单调性与复合函数的单调性判断函数f(x)的单调性.

点评：解答本题的关键：（1）判断函数的奇偶性通常利用定义，但必须要先判断函数的定义域是否关于原点对称；（2）确定函数的单调性时，要注意化简函数的解析式，并利用复合函数的单调性进行判断.

2 判断函数是增函数还是减函数

对于一个函数，如果知道了其单调性，则很容易判断出其是增函数还是减函数.

例4 （2014 陕西卷）下列函数中，满足“f(x+y)=f(x)f(y)”的单调递增函数是( ).

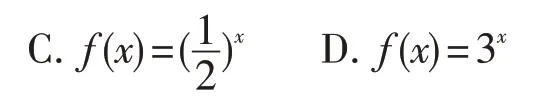
解析：根据各选项知，选项C, D 中的指数函数满足f(x+y)=f(x)·f(y),又f(x)=3x是增函数，故应选D.

点评：因为ax+y=ax·ay，所以指数函数满足f(x+y)=f(x)f(y)，把握这一点是顺利解题的关键，同时还要注意函数单调性的灵活运用.

3 比较大小

待比较的两个数或式子是同一个函数的函数值，常借助于函数的单调性来进行比较，有时需要先构造函数.

例5 设f(x)=x2+bx+c对任意的实数t，都有f(2+t)=f(2-t)，试判断f(1)、f(2)、f(4)的大小.

解析：由f(2+t)=f(2-t)知函数f(x)的图像关于直线x=2 对称，且f(x)在[2, +∞)上是增函数，所以f(2)＜f(3)＜f(4)，而f(1)=f(2-1)=f(2+1)=f(3)，故有f(2) ＜f(1)＜f(4).

例6 （2020全国Ⅱ卷）若2x-2y＜3-x-3-y,则( ).

点评：解答本题的关键点（1）对于结构相同（相似）的不等式，通常考虑变形，构造函数；（2）利用指数函数与对数函数的单调性得到关于x,y的大小关系及ln(y-x+1)的符号.

例8 （2019 全国Ⅰ卷）已知a= log20.2,b=20.2,c=0.20.3，则（ ）.

A.a＜b＜cB.a＜c＜bC.c＜a＜bD.b＜c＜a

解析：因为a= log20.2 ＜0,b= 20.2＞1,c= 0.20.3∈(0,1)，所以a＜c＜b.应选B.

点评：破解此类考题，通常寻找中间变量0,1进行估算，即可比较大小.

点评：对数值的大小比较方法,①化为同底的对数后利用函数的单调性进行比较；②利用作差或作商法比较；③利用中间值（0或1）比较.

4 求值

对于某些待求代数式的值，可视为相应函数的一个特殊值，再利用该函数的单调性，把函数值的相等转化为自变量的相等，进而巧妙获解.

解析:把等式4y3+sinycosy+a=0 化为(2y)3+sin(2y) +2a=0，发现x3+sinx与(2y)3+sin(2y) 结构相似，两式可以统一到函数f(t)=t3+sint上来，因此f(x)=f(-2y) =2a,而f(t)在R 上是增函数，所以x=-2y，x+2y=0,cos(x+2y) =1.

5 求值域

利用函数的单调性求函数的值域或最值有时会显得非常简捷、易懂.

例13 求函数f(x)=2x+1+的值域.

解析：易知函数的定义域为[2, + ∞).∵函数y=2x+1 与y=x-2 在[2, + ∞) 上均为增函数，∴函数f(x)=2x+1 +x-2 在定义域为[2,+∞)上也是增函数.∴f(x)min=f(2) =5，故所求函数的值域为[5,+∞).

6 求最值

例14 已知f(x) 为奇函数，对于任意x，y∈R 都 有f(x+y) =f(x) +f(y) ，且x＞0 时，f(x) ＜0，f(1) =-2,求f(x)在x∈[-3,3]上的最值.

解析：设0 ＜x1＜x2≤3，则x2-x1＞0，∴f(x2-x1)＜0，令x=x2-x1，y=x1，代入f(x+y) =f(x)+f(y) 得：f(x2) =f(x2-x1)+f(x1)＜f(x1). ∴f(x) 在[0, 3] 上是单调递减函数. ∵f(x) 在[-3, 3]上是奇函数，∴f(x)在[-3, 0] 上也是减函数，即f(x)在[-3, 0]上 是 减 函 数. ∴f(x)max=f(-3)=-3f(1) =6,f(x)min=3f(1)=-6.

7 解不等式

有些不等式是由抽象函数式组成的，通过单调性才能转化为自变量的不等式，进而求出不等式的解.

例16 已知f(x)对任意的x,y∈R 都满足条件f(x)+f(y) =2+f(x+y) ，且当x＞0时，f(x)＞2，f(3) =5.解不等式f(a2-2a-2)＜3.

解 析：设x1＜x2，则x2-x1＞0. ∵当x＞0 时，f(x) ＞2，∴f(x2-x1)＞2. ∵f(x2)=f[(x2-x1)+x1] =f(x2-x1) +f(x1)-2 ＞2+f(x1)-2=f(x1)，即f(x2) ＞f(x1).∴f(x)为单调增函数.∵f(3)=f(2+1)=f(2)+f(1)-2=[f(1)+f(1)-2]+f(1)-2=3f(1)-4,又∵f(3)=5，∴f(1) =3.∴f(a2-2a-2) ＜f(1)，∴a2-2a-2 ＜1，即a2-2a-3 ＜0 ，解得- 1 ＜a＜3.故不等式的解为-1 ＜a＜3.

8 证明不等式

点评：原不等式等价于⇒am+n+bm+n≥ambn+anbm⇔(am-bm)(an-bn) ≥0，这可由幂函数y=xα(α＞0)在(0, +∞) 上递增而得到. 该题可拓展：令m=sin2α,n=cos2α，则a+b≥asin2αbcos2α+acos2αbsin2α.

9 解方程

点评：求解此类问题可分两步进行，先通过观察找出其特解x0，然后等价转化为f(x) =a(a为常数) 的形式，然后根据f(x)的单调性得出原方程的解.

例20 解方程3x+4x=5x.

10 确定参数的取值范围

例21 设x∈[0,1], 不等式x2-2mx+2m+1＜0恒成立，求m的取值范围.