一种采用遗传算法优化Chaboche模型的转子轮盘疲劳寿命预测方法
2022-05-25史昱昆王恭义叶笃毅
史昱昆 王恭义 程 凯 叶笃毅
(1.浙江大学化工机械研究所;2.上海汽轮机厂有限公司)
在发电设备中,单缸汽轮机相比多缸汽轮机具有成本低、热效率高及结构紧凑等优点[1]。作为单杠汽轮机的关键部件,一体化转子在服役时需要满足快速启停、变负荷等要求。 在上述交变载荷作用下,转子轮盘应力集中部位(如轮槽齿根)通常存在明显的平均应力,并伴随启停过程出现平均应力循环松弛行为[2,3],因此,在一体化转子的抗疲劳设计中,如何考虑平均应力的影响成为重要的研究内容。
对于平均应力松弛的定量描述,目前工程上主要有两类常用方法:一类是经验模型,另一类是循环塑性本构模型[4]。 由于循环本构模型只需开展少量试验就能完整模拟材料的应力应变行为,近年来已被越来越多地用于描述疲劳载荷下平均应力循环松弛[5]。 其中,Chaboche模型是目前应用广泛的循环本构模型之一[6]。 Chaboche模型最初采用了3级背应力形式。 近年来,为了进一步提高模型的预测精度, 在3级背应力基础上又发展了多级背应力模型[7]。 例如:姜金朋等采用4级背应力模型预测了CS1026 材料的单轴棘轮效应[8];Mahmoudi A H等提出5级背应力模型来改进Chaboche模型的预测能力[9];Ohno N和Wang J D采用分段线性划分方式,发展了级数更多(8级,12级)的背应力模型[10],但随着背应力级数增加,也带来了模型参数大幅增加、参数确定困难等问题。 为了克服传统参数确定方法(如试验法结合试错法[11])存在的求解精度低的问题,近年来许多学者引入了遗传算法来优化Chaboche本构模型中的参数。例如,Nath A等通过对稳定滞回环获取的Chaboche参数进行基因算法优化, 提高了多种CSMs材料棘轮效应的模拟精度[12]。 Mal S等分别采用试错法和基因算法模拟20MnMoNi55钢的滞回环,结果表明:Chaboche模型对参数的敏感程度很高, 参数经过优化后使得结果更为精确[13]。Mahmoudi A H等采用多目标基因算法,将每个循环的最大应变考虑到误差函数中,模拟了多种材料的棘轮效应[14]。 Rouse J P等采用单目标基因算法, 预测了P91钢在600 ℃下的应力应变响应,取得了较好的效果[15]。 由此可以看出,采用遗传算法优化Chaboche本构模型参数能够显著提高疲劳寿命预测的精度,具有广阔的应用前景。
笔者针对某汽轮机一体化转子轮盘的抗疲劳设计需要,采用局部应变法,并结合基于遗传算法优化的8级背应力Chaboche模型,来研究考虑平均应力动态松弛行为的轮盘轮槽疲劳寿命预测方法。
1 基于Chaboche模型的转子轮盘疲劳寿命预测方法
1.1 Chaboche模型及其参数确定算法
Chaboche模型基于Von Mises屈服准则,其表达式为:
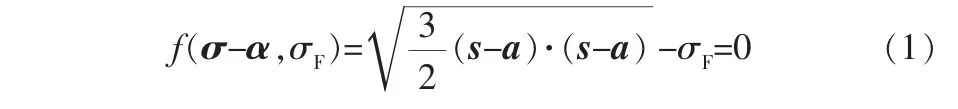
式中 a——偏背应力张量;
s——偏应力张量;
α——背应力张量,表示屈服面的中心;
σ——应力张量;
σF——摩擦应力,表示屈服面的半径。
根据广义正交性假定,塑性流动增量的方向为屈服面的法线方向,塑性应变增量dεp为:
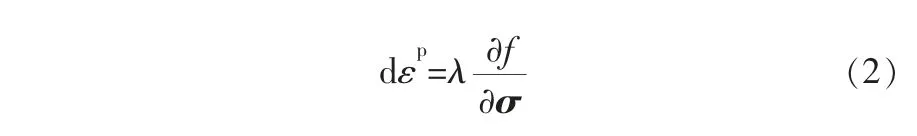
其中,∂f/∂σ表示屈服面的法线方向;λ为塑性乘子。
Chaboche随动强化率认为式(1)中的总背应力α可以划分为多个分背应力αi, 每个分量都符合Armstrong随动强化率,即:
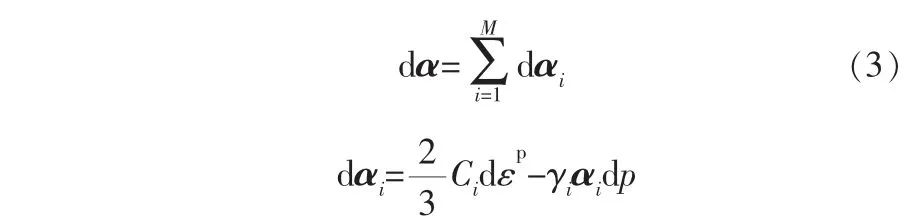
其中,M为背应力级数;Ci和γi为材料参数;p为累积塑性应变。
式(1)中的摩擦应力σF通常采用Voce单级同性硬化率描述,即:
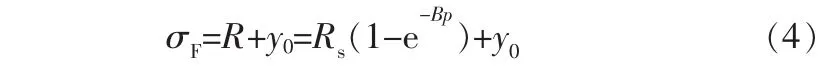
其中,R表示各向同性应力;y0表示初始屈服应力;Rs表示R能够达到的最大值;B表示R达到稳定的速度。
大量研究表明: 上述Chaboche模型的模拟准确性很大程度上取决于参数(Ci,γi,Rs,B)的精确性。 但由于Chaboche模型具有参数多、 各参数之间关系复杂且相互制约等特征,模型参数和应力应变之间是一个非常复杂的非线性函数关系。 采用传统方法(试验法结合试错法)求解上述参数,往往因背应力分段不明确、试验数据分散性大等原因,导致模拟结果出现较大误差[16]。
近年来, 遗传算法被应用于确定Chaboche模型参数。 通过选择、交叉及变异等一系列操作对模型参数进行迭代进化,从而达到提高参数求解精度的目的。 基于遗传算法优化Chaboche模型参数可归结为以下3个步骤:
a. 确定参数初值。 首先采用试验法求得Chaboche模型参数初值。 参考文献[17],随动硬化参数(Ci,γi)取值范围一般服从依次减小的规律(C1>C2>C3>Ci,γ1>γ2>γ3>γi),同性硬化参数Rs取值范围可根据材料循环软化/硬化特性进行判断,b取值一般为负。
b. 适应度判断。综合模拟效果和计算效率选择合适的Chaboche模型适应度函数, 即模型模拟值(εmodel,σmodel)和试验值(εexp,σexp)的加权差值,差值越小代表参数求解越精确。
c. 进化操作。 在步骤b的基础上,通过选择、交叉、 变异操作, 诞生出新一代Chaboche模型参数。 重复步骤b、c,直到模型参数收敛到规定精度为止。
采用遗传算法确定Chaboche模型参数的流程如图1所示。
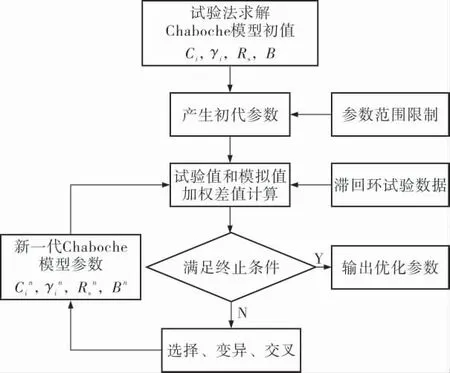
图1 确定Chaboche模型参数的遗传算法流程框图
1.2 基于Chaboche模型的疲劳寿命预测方法
基于Chaboche模型预测转子轮盘疲劳寿命的方法主要可归纳为:采用局部应力应变近似计算公式联立Chaboche模型, 将作用在转子轮盘的载荷转化为轮盘危险部位(如轮槽齿根)的局部应力、应变;考虑平均应力动态松弛行为,同时结合平均应力修正模型,进行轮盘危险部位的损伤计算;最终通过损伤累计来预测轮盘疲劳寿命。 上述寿命预测流程如图2所示(图中的SWT模型、统一法引用文献[18,19])。
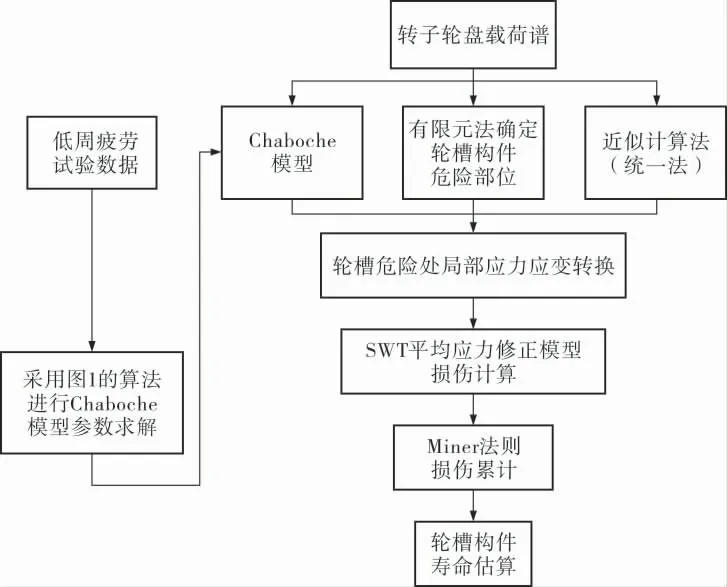
图2 基于Chaboche模型的轮槽构件疲劳寿命预测流程框图
2 试验过程
2.1 光滑试样低周疲劳试验
为了确定Chaboche模型参数,开展了某型轮槽材料的光滑试样单调拉伸试验和应变比为0的应变控制低周疲劳试验。 试验参考相关标准[20],在MTS-810电液伺服疲劳试验机上进行。 该轮盘材料的低周疲劳力学性能参数如下:
屈服强度σy700 MPa
疲劳强度系数σf′ 1 051 MPa
材料弹性模量E 203 GPa
疲劳延性系数εf′ 0.205 1
强度系数K 1 024 MPa
疲劳强度指数b-0.072
应变硬化指数n 0.058 9
疲劳指数c-0.588
2.2 轮槽构件低周疲劳试验
为了验证基于Chaboche模型的转子轮盘疲劳寿命预测方法的准确性,开展了脉动载荷下某型轮槽构件的低周疲劳试验。 图3是该轮槽构件的主要几何尺寸,其中轮槽齿根A、B、C的理论应力集中系数Kt采用有限元法确定, 分别为3.39,3.11,2.39。
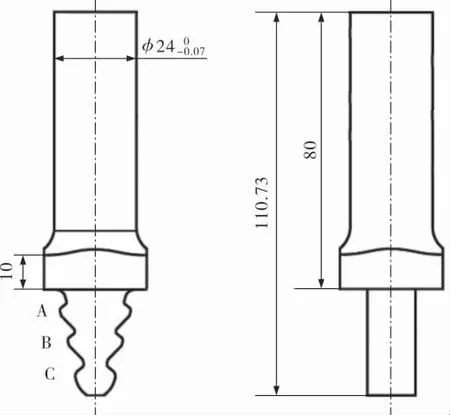
图3 轮槽模拟件几何形状
轮槽构件的疲劳试验在MTS-810电液伺服疲劳试验机上进行, 试验采用应力比为0的轴向载荷控制,正弦波加载。 试验过程中采用长距离显微测试系统实时监测裂纹长度,试验现场与轮槽构件裂纹的测量结果如图4所示。 记轮槽缺口部位出现长度为0.5 mm裂纹的循环周次为裂纹萌生寿命。

图4 试验现场与轮槽构件裂纹测量
3 某型轮槽构件的疲劳寿命预测与试验验证
采用基于Chaboche模型结合遗传算法的转子轮盘疲劳寿命预测方法(图2),对某型轮槽构件进行了疲劳寿命预测, 并将预测结果与试验结果进行比较。
3.1 Chaboche模型参数确定
确定Chaboche模型(式(4))中的R。 参考文献[21]中的方法,通过试验数据提取摩擦应力。 图5为某典型应变幅下轮槽材料最初1/4循环(单调拉伸阶段)和后续疲劳循环的摩擦应力拟合曲线。
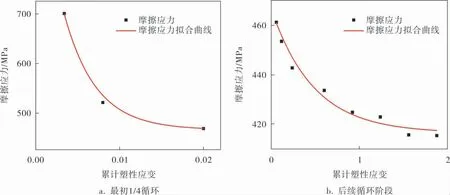
图5 轮槽材料的摩擦应力拟合曲线
从图5可以看出:在最初1/4循环,当累计塑性应变增加到0.02时,摩擦应力从700 MPa迅速衰减到460 MPa,之后在循环载荷作用下呈现缓慢减小特征。采用叠加的Voce模型[22],分别对上述两个阶段摩擦应力(σF)进行拟合,其表达式可写成:
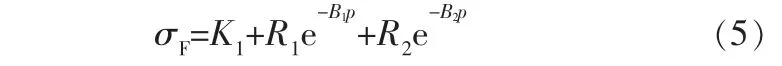
其中,K1、R1、B1、R2和B2为拟合参数。
确定Chaboche模型中的随动硬化参数(Ci,γi)则参考文献[23]中的方法。 为了保证精度,本次研究将背应力划分为8级,如图6所示。 其中,第1、2级背应力描述小应变阶段,第3~5级背应力描述中应变阶段,第6~8级背应力描述大应变阶段。
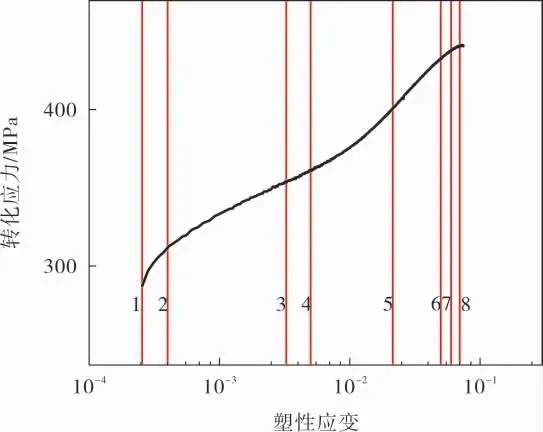
图6 8级背应力的划分
轮槽材料的随动硬化参数初值列于表1中。
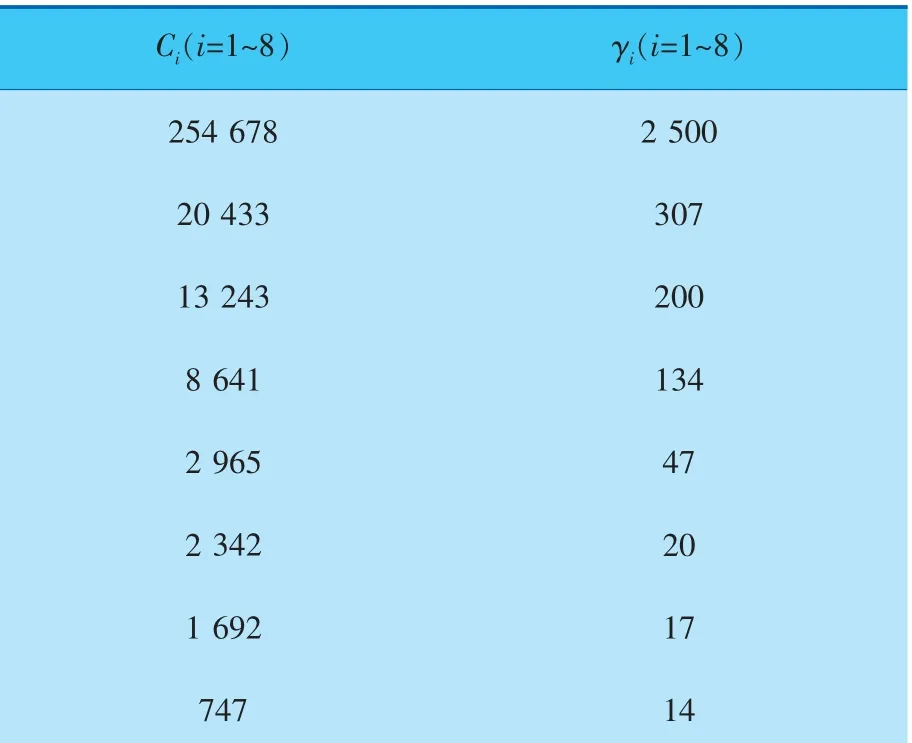
表1 Chaboche模型参数初值
前4个阶段的各向同性硬化参数初值R1=287、B1=293、R2=287、B2=239、K1=465、R3=321、B3=375、R4=50、B4=2、K2=416。
采用图1中的遗传算法流程, 结合2.1小节中材料低周疲劳试验结果, 可进一步优化Chaboche模型中的26个参数。 本次算法参数设置基于Matlab的Optimtool遗传算法工具箱, 自行编写了适应度函数。 采用二进制编码,初始种群数量根据变量数(26个)选为300。 根据初值大小设置参数范围限制以加快收敛速度。 为保证8个背应力分量充分发挥作用,本算法选用应变幅1.2%的滞回环数据,试验数据选取前10个滞回环。 其中,误差函数按下式计算:
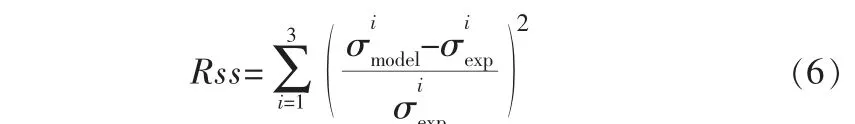
其中,σ1表示峰值应力,σ2表示谷值应力,σ3表示平均应力。
式(6)由3个分误差函数组成,平均应力误差用来保证平均应力的模拟精度,峰值/谷值应力误差则控制滞回环的形状。
采用排名选择法, 交叉操作采用单点交叉,交叉概率定为0.5,变异概率定为0.02。 终止条件定为进化到2 000代或误差小于0.000 01。
经过上述遗传算法优化的轮槽材料的随动硬化参数列于表2。
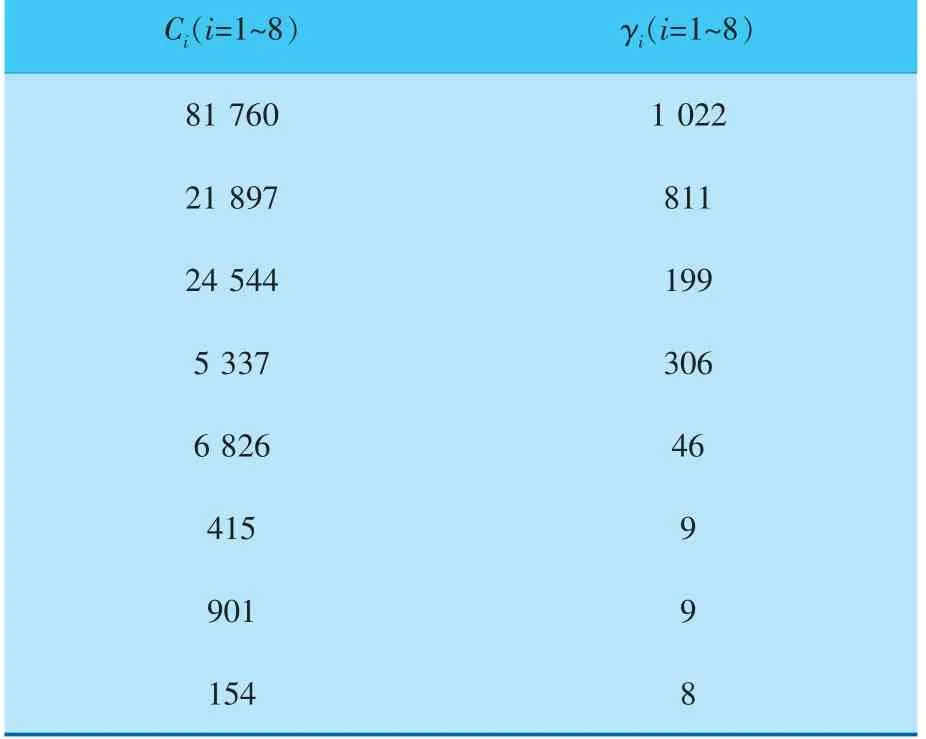
表2 Chaboche模型优化后参数
前4个阶段的各向同性硬化参数优化后数值R1=261、B1=253、R2=261、B2=207、K1=458、R3=38、B3=1.88、R4=-5.2、B4=-0.355、K2=460。
3.2 轮槽材料的平均应力松弛行为模拟
为了验证Chaboche模型描述轮槽材料循环本构关系的精确性, 采用表2中优化后的本构模型参数对轮盘材料的循环滞回环进行了模拟。 图7给出了前10个滞回环的模拟值和试验值的比较。可以看出,采用遗传算法优化Chaboche模型参数能很好地模拟不同应变幅下最初1/4循环和后续滞回环形状(包括峰值/谷值应力的演化趋势和滞回环弹塑性过渡阶段)。
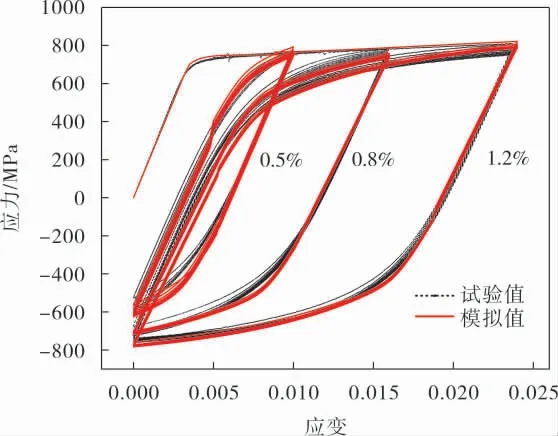
图7 不同应变幅下滞回环模拟值与试验值的比较
为了进一步验证Chaboche模型模拟平均应力松弛行为的精度,采用优化后的本构模型参数计算不同应变幅下的平均应力,并与试验值进行比较,结果如图8所示。 由图8可知:在各种应变幅下,平均应力均发生了明显的松弛,应变幅越大,初始平均应力越小,而松弛速率越大。 从图8中还可以得出: 采用优化参数的Chaboche模型总体能够准确预测较宽应变幅范围(0.4%~1.0%)的轮槽材料平均应力松弛行为。
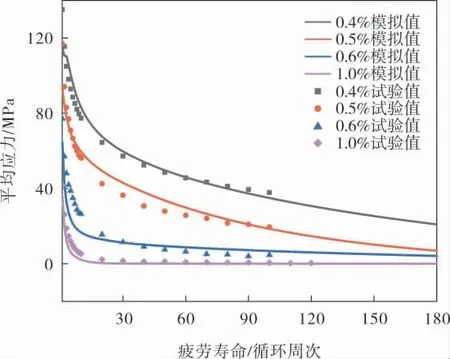
图8 不同应变幅下平均应力松弛模拟值与试验值的比较
3.3 轮槽构件疲劳寿命预测
表3给出了基于8级背应力Chaboche模型的轮槽构件疲劳寿命模拟值、 试验值及其相对误差。图9是疲劳寿命预测值与试验值的比较。
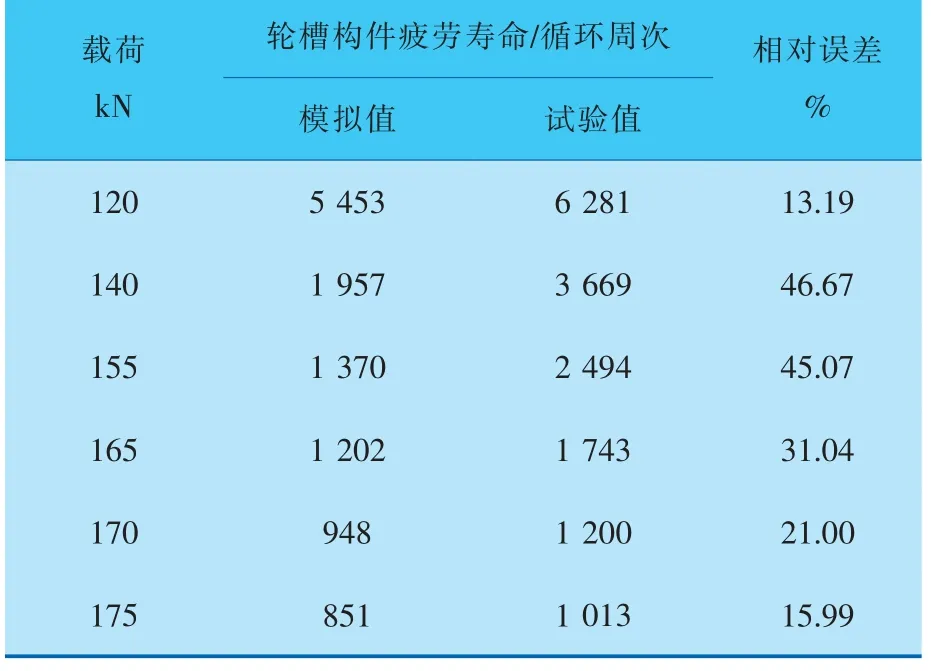
表3 轮槽构件疲劳寿命模拟值与试验值
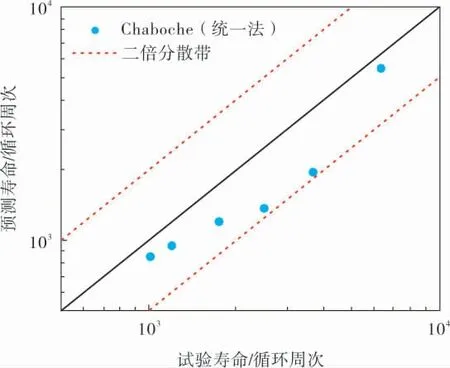
图9 轮槽构件疲劳寿命预测值与试验值的比较
从图9可以看出, 基于8级背应力Chaboche模型的转子轮盘疲劳寿命预测方法总体能够获得与试验寿命较为一致的结果,在本文研究的载荷条件下, 预测寿命与试验寿命在二倍分散带之内。
4 结论
4.1 基于局部应变法, 采用遗传算法优化Chaboche模型参数, 建立起一种预测转子轮盘疲劳寿命的新方法。
4.2 采用参数优化的Chaboche模型模拟了某型轮盘材料在多种应变幅下的滞回环形状和平均应力松弛行为,通过与试验值相比较证明了两者一致性较好。
4.3 采用笔者建立的转子轮盘疲劳寿命预测方法对某型轮槽构件开展了疲劳裂纹萌生寿命预测。 通过与试验结果的比较可知,两者误差在二倍分散带之内。
