基础不均匀沉降对球罐支柱影响的试验研究
2022-05-25吴泽民周国强
吴泽民 周国强 戴 光
(东北石油大学机械科学与工程学院)
建造在沿海回填土地基的大型钢制球罐在运行一段时间后会出现不同程度的基础沉降现象,导致球罐发生倾斜,支柱产生沉降差,使各支柱受力不均匀并产生附加内应力,这成为引起球罐结构损伤的重要原因之一,特别是存储石化原料的大型球罐,一旦发生事故将造成灾难性的后果[1,2]。
近年来,越来越多的学者开始关注基础沉降给球罐带来的安全问题。 Gao H L等通过有限元计算,对出现基础不均匀沉降的在役液化石油气球罐进行应力分析和评定,得到基础沉降对球壳和支柱应力分布的影响规律[3]。 黄金国等采用计算分析方法对多台发生整体倾斜的球罐进行支柱和拉杆应力校核,对不同类型球罐的最大倾斜度给出不同的结论[4]。 周蓓蓓等采用数值模拟方法对球罐4种基础不均匀沉降形式进行有限元计算与分析,得到沉降后球罐支柱反力不均匀度和支柱垂直压缩应力的变化规律[5]。 Ramaneyulu K等对球形储罐在内压、地震载荷和风载荷组合工况下进行了有限元分析并对其可靠性进行评价[6]。高红利等通过计算分析,探讨了球罐基础沉降差对支柱稳定性的影响,并提出增强球罐支柱稳定性的有效措施[7]。 李志海等对发生基础不均匀沉降的在役LPG球罐建立弹塑性模型, 分析支柱应力在材料非线性下的变化,对球罐的安全性进行评定,为球罐基础不均匀沉降的安全评估提供了技术指导[8]。
目前,对于大型球罐基础不均匀沉降的研究多以计算分析和数值模拟为主,但缺少必要的试验研究进行验证。 在此,笔者通过1.5 m3钢制球罐模型在基础不均匀沉降作用下的试验研究,探讨基础整体倾斜、局部地基沉降情况下对球罐支柱应力分布产生的影响及其规律,以期为实际工程提供安全的分析方法和一定的借鉴依据。
1 试验
1.1 试验设计
试验模型的原型为2 500 m3丙烷球罐, 设计压力为1.8 MPa,由均匀分布的10根支柱以赤道正切式结构支撑,球壳与支柱连接处采用U形托板。综合考虑试验场地、 试验精度及加载工况等因素,试验模型的材料与原型保持一致,确定几何相似比CL=Lm∶Lp=1∶12(Lm、Lp分别表示球罐模型尺寸和球罐实际尺寸), 按相似比计算得到模型主部件参数见表1。

表1 球罐试验模型主部件参数规格
基础不均匀沉降试验分为基础整体倾斜和局部沉降两个部分,为保证试验过程中对倾斜角度和沉降位移量的精确控制,设计采用液压伺服系统加载。 球罐模型的基础部分由6个液压油缸控制, 其中1号油缸与模型基础整体相连,2~6号油缸与球罐模型的5根支柱相连。 通过控制1号油缸的顶升,可实现对基础整体倾斜的控制,如图1所示;控制2~6号油缸的升降,可实现球罐模型5根支柱的局部沉降控制,如图2所示。

图1 基础整体倾斜试验示意图

图2 局部沉降试验示意图
1.2 试验准备
试验采用BE120-5AA型应变片, 电阻值为120.0 Ω±0.1 Ω, 灵敏度系数为2.14%±1.00%,选用工作片补偿法 (即沿支柱轴向粘贴一枚应变片,横向垂直粘贴另一枚应变片)进行测量。 应变片粘贴在支柱U形托板下方100 mm处,测点布置在支柱外侧, 用BDI无线动态电阻应变仪采集应变数据。基础倾角测量选用Jewell 700系列高精度倾角传感器,量程±10°,分辨力0.2″,布置在球罐模型基础底部以测量模型基础倾斜角度。
1.3 试验方案
为研究球罐在不同沉降形式下支柱的受力性能,基于GB 12337—2014《钢制球形储罐》[9]中的基础沉降测试步骤, 每种试验方式分为4种工况进行。
1.3.1 整体倾斜试验
基础倾斜试验加载时,球罐基础沿箭头方向(图3)倾斜,各支柱标号顺序如图3所示。 倾斜角度选取0、2、4、6、8°,每种角度停歇1 min,记录各工况(表2)下支柱的应变值。

图3 球罐支柱标号顺序示意图

表2 基础整体倾斜试验工况
1.3.2 局部沉降试验
GB 12337—2014规定相邻支柱基础沉降差值不大于2.0 mm。局部沉降试验加载时,选取1#支柱施加沉降位移,每级位移增量为0.5 mm(即0.0、0.5、1.0、1.5、2.0 mm),加载停歇1 min,记录1#支柱沉降量和2#~10#支柱的应变值。 试验工况见表3。

表3 1#支柱沉降试验工况
1.4 计算依据
根据广义胡克定律,支柱在弹性变形范围内时主应力与应变之间的关系式为:

式中 E——支柱材料的弹性模量;
σx、σy——x、y方向的主应力;
εx、εy——应变片在x、y方向的测量应变值;
μ——支柱材料的泊松比。
根据试验记录的应变数据,按上述公式即可计算得到每个测点的主应力。
2 试验结果与分析
2.1 整体倾斜试验
2.1.1 倾斜角度对支柱应力的影响
4种工况下球罐模型支柱的测点应力-倾斜角度曲线如图4所示。
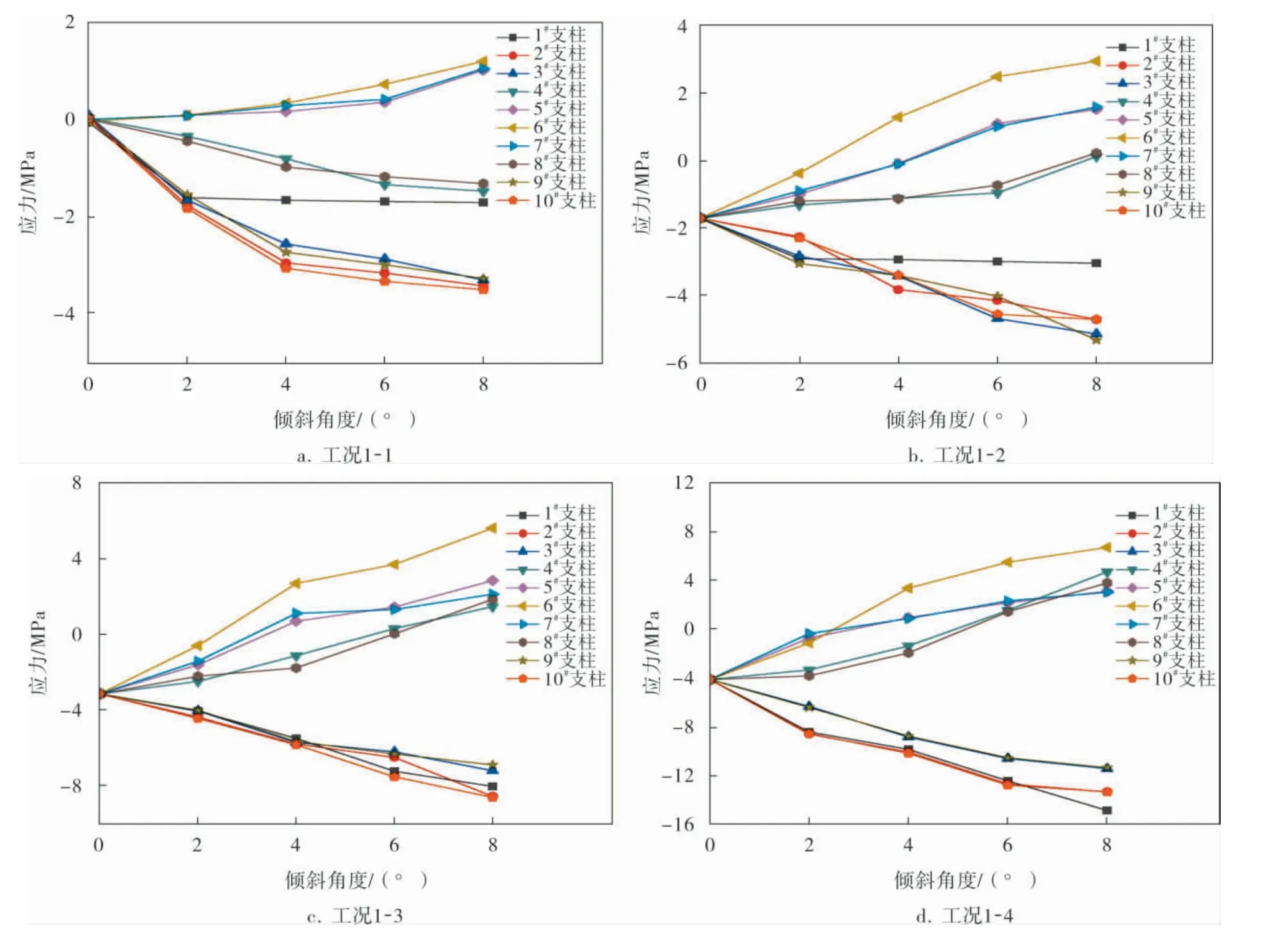
图4 4种工况下球罐模型支柱的测点应力-倾斜角度曲线
由图4a可看出, 随着基础倾斜角度的增大,1#~4#支柱、8#~10#支柱的轴向压应力逐渐增加,5#~7#支柱测点受轴向拉应力且随着倾斜角度的增大而增加。 这是由于基础倾斜后球罐整体重心偏移,导致1#~4#支柱、8#~10#支柱承载更多的球罐质量,而5#~7#支柱受弯矩的影响,在支柱外侧产生轴向拉应力。
由图4b~d可看出,随着基础倾斜角度的增大,1#~3#、9#、10#支柱的轴向压应力不断增加,4#~8#支柱的轴向压应力逐渐减小, 当基础倾斜4°时,5#~7#支柱的轴向压应力开始转变为轴向拉应力, 当基础倾斜8°时,4#~8#支柱全部受轴向拉应力, 其中6#支柱的轴向应力差值最大。 由此可知,当基础倾斜角度较大(一般不小于2°)时,球罐和液体介质的重力作用于基础低处的支柱上, 而基础高处的支柱由于产生附加弯矩, 支柱受到压应力逐渐较小并且随着倾斜角度的增大逐渐转变为轴向拉应力。
2.1.2 充液高度对基础倾斜后支柱应力的影响
当基础整体倾斜时,球罐模型支柱的测点应力-充液高度曲线如图5所示。
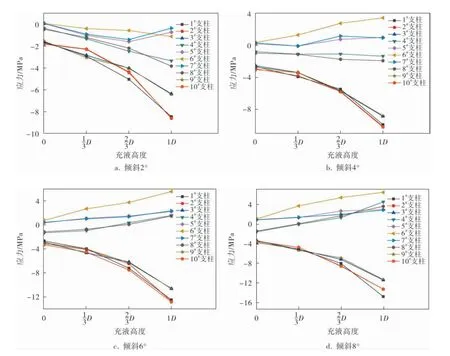
图5 球罐模型支柱的测点应力-充液高度曲线
由图5a可看出,当基础倾斜角度为2°时,随着球罐模型充液高度的增加,球罐各支柱轴向压应力增大, 在液位高度为D、1D时,1#、2#、10#支柱测点应力幅值突然变大,其他支柱轴向压应力增幅较小且比较平缓, 在液位高度为1D时,5#、7#支柱轴向压应力有减小的趋势。
由图5b可看出,当基础倾斜角度为4°时,随着球罐模型充液高度的增加,1#~3#、9#、10#支柱轴向压应力逐渐增大,4#、8#支柱轴向应力变化较小,5#~7#支柱受轴向拉应力并逐渐增大。
由图5c、d可看出,当基础倾斜角度为6、8°时,随着充液高度的变化,球罐各支柱轴向应力变化规律基本一致,即基础低处的支柱(1#~3#、9#、10#)轴向压应力增大,在充液高度为1D时应力幅值变大,基础高处的支柱(4#~8#)受轴向拉应力逐渐增大,其中6#支柱轴向拉应力增幅最大。
2.2 局部沉降试验
2.2.1 沉降量对支柱应力的影响
在局部沉降试验中, 选择1#支柱施加沉降位移, 故试验测点为2#~10#支柱,4种工况下球罐支柱测点应力-沉降量曲线如图6所示。 由图6可看出,4种工况下2#~10#支柱测点应力变化规律基本相同,各支柱测点应力值变化不大。当1#支柱发生沉降时, 随着沉降量的增加,2#、3#、9#、10#支柱轴向压应力突然增大, 且呈线性关系。 其中,与1#支柱相邻的2#、10#支柱轴向压应力幅值较大,3#、9#支柱轴向压应力幅值较小,4#~8#支柱轴向应力变化较小。 由此可知,单支柱沉降时,对与之相邻的4根支柱的影响较大,且随着距离沉降支柱的变远影响程度逐渐变小。

图6 4种工况下球罐支柱测点应力-沉降量曲线
2.2.2 充液高度对局部沉降后支柱应力的影响
1#支柱沉降量为0.5 mm时球罐支柱测点应力-充液高度曲线如图7所示。 由图7可知,1#支柱发生沉降时,随着球罐充液高度的增加,2#~10#支柱的轴向压应力逐渐增大,这是因为支柱在液体重力作用下产生了压缩和弯曲,液位越高,重力载荷越大,支柱轴向应力越大。
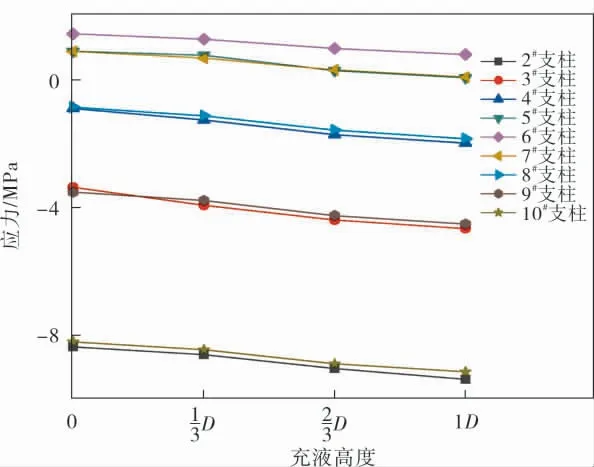
图7 沉降量为0.5 mm时球罐支柱测点应力-充液高度曲线
3 基础不均匀沉降下球罐有限元应力分析
利用ABAQUS有限元软件, 按试验模型参数建立三维有限元模型如图8所示。 球壳和支柱采用实体单元C3D8R(八节点线性六面体单元),拉杆采用桁架单元T3D2(两节点线性杆单元),考虑到球壳与支柱连接处的结构和受力比较复杂,对上支柱的网格进行加密,球壳本身在试验过程中受力较均匀,进行粗略的网格划分。 选取工况1-4时基础整体倾斜4°的试验条件和工况2-4时1#支柱沉降量2.0 mm的试验条件施加相应的载荷和边界约束,采用线性静力分析方法得到两种工况下球罐支柱的应力分布如图9、10所示。

图8 球罐模型及网格划分

图9 工况1-4应力分布云图

图10 工况2-4应力分布云图
将有限元计算结果与试验测试结果进行比较(表4、5)。

表4 工况1-4有限元计算结果与试验测试结果对比

表5 工况2-4有限元计算结果与试验测试结果对比
由表4、5可知, 有限元计算结果与试验测试结果较接近,误差均在±10.0%以内。 因此,试验模型和试验过程可基本真实、全面地反映球罐在基础倾斜和局部沉降两种情况下支柱的受力情况。
考虑到球罐最危险的工况是液压试验,基于上述有限元模型,液压试验压力为:

式中 p——设计压力,MPa;
pT——液压试验压力,MPa。
分别计算球罐基础整体倾斜8°时液压工况和局部沉降2.0 mm时液压工况下的球罐支柱极限应力,结果见表6。 由表6可知,液压工况下,基础整体倾斜对各支柱的最大应力产生不同影响,处于基础低处的支柱最大应力有所增加,基础高处的支柱最大应力变化幅值很小,各支柱最大应力在许用应力范围内,球罐处于稳定状态。 局部沉降2.0 mm时, 与1#支柱相邻的两个支柱的最大应力突变很大, 最大应力超过材料的屈服强度,极有可能发生局部屈服,造成球罐结构损伤,其余支柱随着与1#支柱距离的变远而迅速恢复到正常应力范围内。 可见,当发生局部沉降时,相邻两个支柱应作为重点检测部位。

表6 不同液压工况下球罐支柱的最大应力
4 结论
4.1 综合考虑试验场地、试验条件等因素,确定试验模型几何相似比为1∶12, 建立球罐基础不均匀沉降试验台,设计基础整体倾斜和局部支柱沉降两种试验方案,通过计算发现,试验测试结果与有限元计算结果基本一致,说明该试验模型和试验过程可有效反映球罐在基础整体倾斜和局部沉降两种情况下支柱的受力情况。
4.2 球罐基础整体倾斜试验结果表明,球罐各支柱随着倾斜角度的增大, 球罐重心发生偏移,导致各支柱沿倾斜方向的弯矩增大。 处于基础低处支柱的轴向压应力不断增加,基础高处支柱的轴向压应力逐渐减小,在倾斜角度为4°时,转为轴向拉应力,其中基础最高处支柱的轴向应力差值最大。 基础整体倾斜时,随着液位高度的增加,球罐整体质量变大,产生的附加弯矩变大。
4.3 球罐局部支柱沉降试验结果表明,支柱附加应力的幅值随距离沉降支柱的远近而变化,与沉降支柱相邻的支柱上产生的附加应力最大,且与沉降差增大呈线性递增关系;距离沉降支柱较远的支柱受到影响逐渐减小。 局部支柱沉降时,随着液位高度的增加,球罐整体质量变大,各支柱轴向压应力增大。
4.4 基于ABAQUS有限元软件对球罐模型进行液压试验工况分析,结果表明基础整体倾斜8°时,球罐各个支柱最大应力值均在许用应力范围之内,球罐模型处于稳定状态;局部支柱沉降2.0 mm时,与之相邻的两个支柱的最大应力超过支柱材料的屈服强度,支柱极有可能发生局部屈服,球罐处于不安全状态。
