基于Workbench的多级轮盘组件优化设计

邵 帅，郭秩维，储建恒

（中国航发沈阳发动机研究所，沈阳110015）

0 引言

轮盘作为航空发动机的重要关键件，其结构强度关系着发动机甚至飞机的安全性。随着现代航空发动机对性能要求的不断提高，轮盘结构向着质量轻、工作温度和工作转速高的方向发展，对轮盘结构强度设计人员提出更高的要求。

工程上，设计人员在进行轮盘设计的过程中多采用CAD（Computer Aided Design）技术进行建模，由强度专业人员利用CAE（Computer Aided Engineering）技术进行该结构的强度分析，根据分析结果向结构设计人员提出相应的改进建议后，再由结构设计人员进行结构改进，同时还伴随着气动、空气系统、热分析等多个专业的配合与迭代。设计1个轮盘通常要进行多轮次迭代，需要多个专业的设计人员投入大量的时间和精力，一直以来是制约航空发动机研制周期的因素之一。

随着近年来仿真技术的不断提高，基于参数化建模的结构优化设计技术成为现代发动机设计的重要手段[1-5]。采用结构优化设计技术有效提高发动机零部件的设计效率和设计质量，能够缩短航空发动机的研制周期。采用MDO（Multidisciplinary Design Optimization）多学科优化设计技术[6-7]进行复杂零部件结构设计的工程适用性较强，能够考虑发动机实际工作环境下的多物理场耦合的结构优化。

本文通过UG进行参数化建模[8-10]，基于Work-bench与集成的优化软件optiSLang建立热与结构耦合的多物理场优化平台，根据工程实际对多级轮盘进行减质优化设计。

1 轮盘参数化建模技术

在优化前需要对轮盘进行参数化建模，通过改变模型中的参数值就能建立和分析新的结构模型，通过不断迭代求出最佳解。

轮盘具有结构复杂和级数多的特点，在进行方案阶段的结构设计时，静强度评估多采用轮盘子午面的2维模型进行分析，即便如此，单级2维轮盘模型的尺寸参数多达几十个（如图1所示），而整个转子的尺寸参数多达几百个。

图1 单级轮盘参数化

设计变量太多不易获得最优解，因迭代次数较多，为提高优化效率，在结构优化前必须结合工程实际提取对轮盘承载能力和体积影响较大的结构参数。

本文采用成熟的UG软件进行轮盘的参数化建模，并结合工程实际提取轮盘主要设计参数，利用UG的草图约束命令和尺寸约束将其他尺寸参数进行合理约束，以实现轮盘尺寸优化过程中的迭代，单级轮盘主要尺寸参数如图2所示。其他各级轮盘的参数化建模方法与此相同，通过在同一个UG模型中建立多个草图的方法建立包括各级轮盘、封严环等零件的多级轮盘组件。

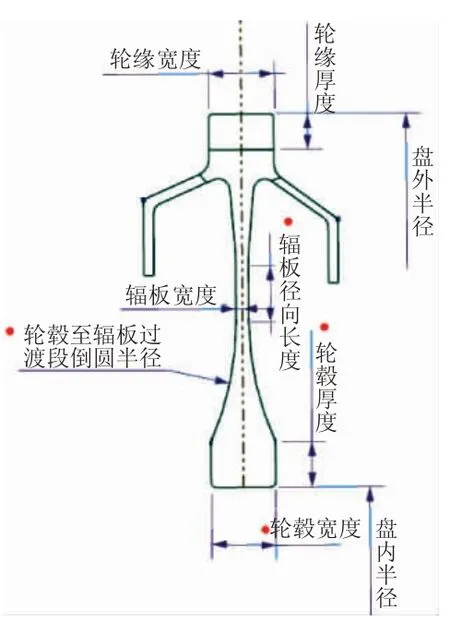
图2 单级轮盘主要尺寸参数

2 轮盘优化策略

2.1 优化设计流程

通过UG进行参数化建模，采用商用有限元软件Workbench进行CAE仿真，利用集成的optiSLang软件进行优化，建立了多物理场、多级轮盘优化设计平台，将轮盘结构优化设计与仿真流程紧密结合，在优化设计的迭代过程中实现各物理场数据的自动传输。轮盘优化过程如图3所示。

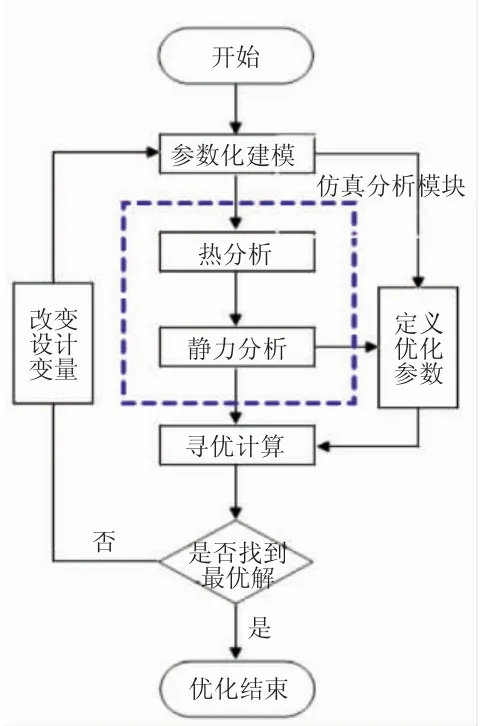
图3 轮盘优化设计过程

在进行多级轮盘组件优化设计时，Workbench调用UG参数化模型，自动在组件连接部位定义接触边界条件，根据实际情况将各级轮盘与封严环等对应的螺栓连接部位定义为绑定约束，对组件进行网格划分，从而进行组件的仿真分析。通过建立多级轮盘组件优化设计模型，在进行热分析、静力分析时可以考虑各零组件之间的相互影响，使模型边界条件更为准确，从而一次性获得准确的优化结果。

仿真分析模块包括热分析和静力分析2部分，首先通过导入的外部温度数据作为输入的载荷进行组件的热分析，再将热分析的计算结果作为温度载荷施加到静强度分析模型的各节点上，模拟轮盘实际工作状态下的热固耦合问题。

OptiSLang提供了多种优化算法，包括梯度算法、自然启发算法及响应面算法，本文采用响应面算法。在进行寻优计算时，首先利用敏感性分析模块基于有限次数的CAE求解建立高质量的响应面，即MOP（最优预测元模型）。该方法通过对多种回归算法进行对比，能够确定拟合精度最佳的回归模型（MOP最优预测元模型），并给出可靠的MOP预测质量评价指标（COP）。在敏感性分析模块中定义设计变量、约束条件以及优化目标建立MOP，再利用MOP替代求解器进行后续的寻优计算。

本文以第2级低压涡轮盘为例给出详细的优化设计参数及优化结果。

轮盘优化数学模型为[11-12]

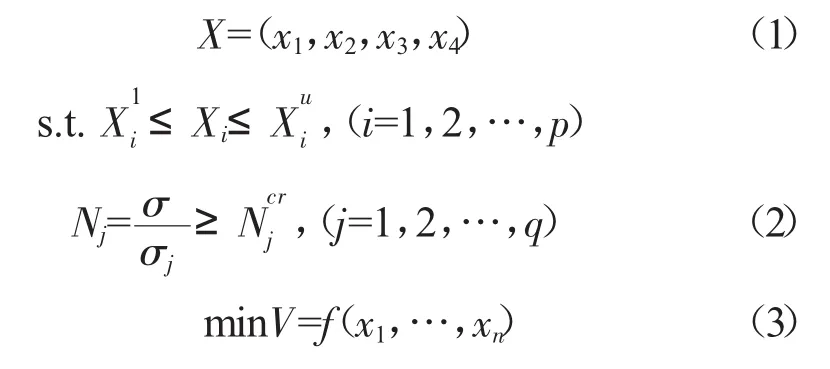
2.2 设计变量

在实际工程设计中[13-16]，轮盘优化还需要考虑以下几方面的问题。

（1）轮盘连接部位尺寸。

盘榫连接部位：通常若叶片结构已确定，盘缘宽度、轮缘凸块高度、盘缘高度3个参数不作为优化变量。

鼓筒连接部位：轮盘鼓筒与封严环和其他级轮盘相连接，该部位尺寸不作为优化变量。

（2）受空间限制的尺寸。

考虑到盘心下方空间限制，减质优化时盘心高度保持不变。

（3）振动问题。

若轮盘过薄，可能存在振动问题，因此辐板宽度保持合理尺寸，不作为优化变量。

综上所述，确定轮盘减质优化的设计变量，并确定设计变量的约束区间，见表1。

表1 轮盘优化设计变量

2.3 约束条件

轮盘减质优化是在轮盘强度和刚度满足要求的基础上获得质量（体积）最低的寻优计算，轮盘强度和刚度主要体现在各项应力指标和盘缘最大径向变形满足设计要求，见表2。

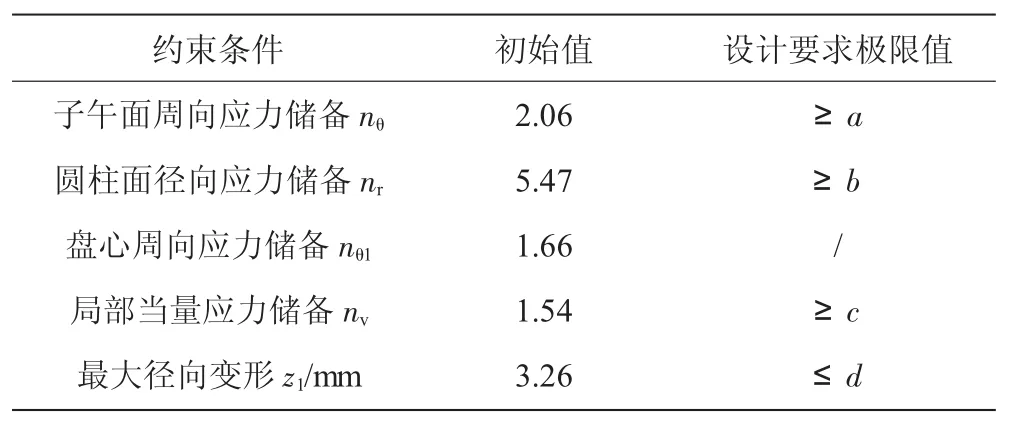
表2 轮盘优化约束条件

2.4 优化目标

在寻优计算时需指定目标函数，轮盘的减质优化设计设置优化目标为质量（体积）最小。

3 结果分析

基于搭建的多物理场轮盘优化平台，对典型的4级低压涡轮盘进行优化设计。低压涡轮盘工作时除离心载荷外还承受较大的热负荷，盘缘到盘心的温度梯度使轮盘沿径向产生较大的热应力，在进行强度分析时必须考虑热应力的影响。优化平台中的热分析模块就能完成结构迭代过程中温度场的计算，考虑热应力的影响，进而完成轮盘组件的热固耦合分析。

轮盘材料选为高温合金GH4169，分析时考虑了温度对材料性能的影响。采用PLANE183单元建立有限元模型，定义轮盘槽底以下部位为周期对称单元，定义槽底以上的轮缘凸块部位为具有一定厚度的平面应力单元进行弹性应力分析，考虑温度场对材料力学性能的影响。按照第2章定义设计变量、约束条件和目标函数进行各级轮盘优化，给出的第2级低压涡轮盘各参数初始值及优化结果见表3。

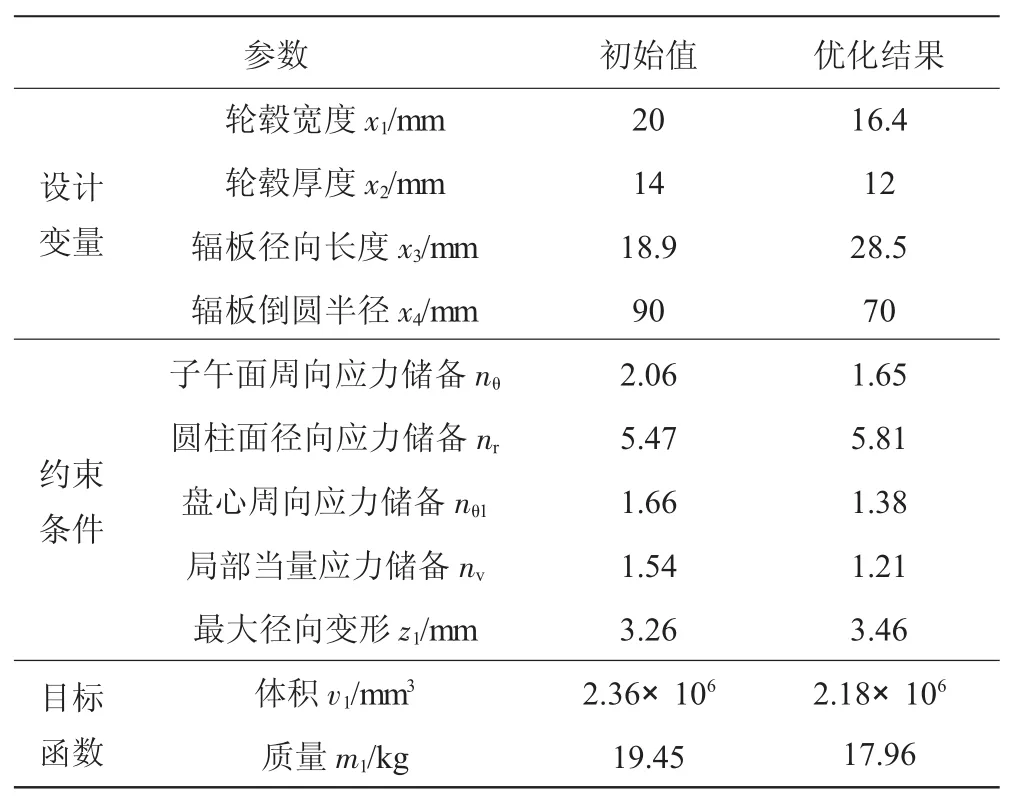
表3 优化结果

轮盘优化前、后结构对比如图4所示。减质优化后该级轮盘轮毂宽度和轮毂厚度降低，辐板倒圆半径降低，优化后该级轮盘质量共减轻1.49 kg。轮盘减质优化后周向应力和径向应力分布如图5所示。

从表2中可见，轮盘圆柱面径向应力储备较高，但为了保证轮盘具有足够的抗振能力，未对轮盘辐板宽度进行减质优化，轮盘周向应力是主要限制条件。低压涡轮转子第1～4级轮盘优化前各级轮盘子午面周向应力储备系数对比如图6所示，优化后各级轮盘子午面周向应力储备系数对比如图7所示。从图中可见，优化前第2级轮盘应力储备偏高，整个涡轮转子各级轮盘的应力储备系数分布非常不均衡，而优化后各级轮盘子午面周向应力储备基本一致，提高了材料的利用率。整个低压涡轮第1～4级轮盘质量共减轻4.45kg。

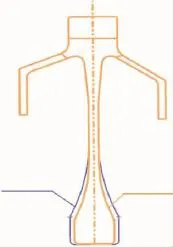
图4 优化前、后轮盘结构对比

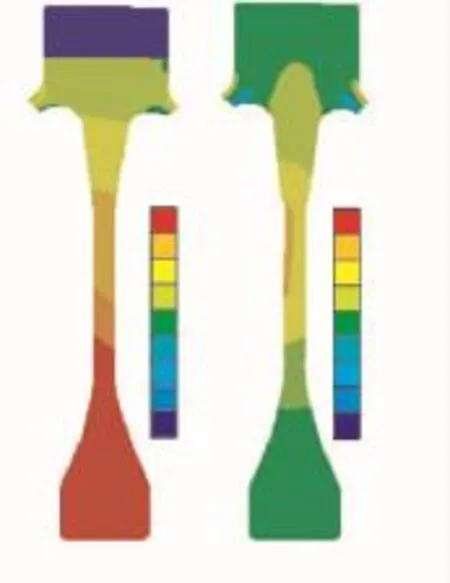
图5 优化后的轮盘结构应力分布

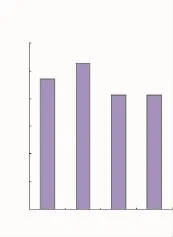
图6 优化前各级轮盘的应力储备

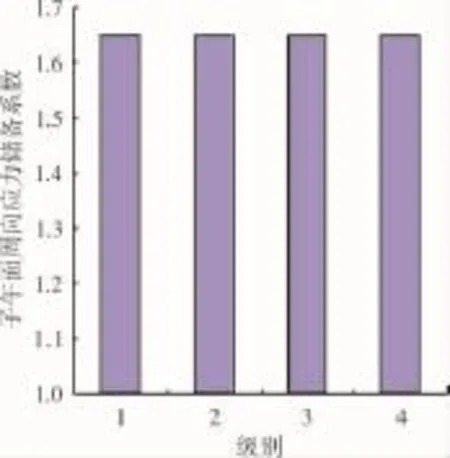
图7 优化后各级轮盘的应力储备

4 结论

针对工程上轮盘组件优化设计的需求，建立热与结构耦合的多物理场优化平台，对多级低压涡轮盘进行优化设计。优化后各级轮盘应力及变形满足设计要求，子午面应力储备分布均匀，提高了材料的利用率，整个低压涡轮第1～4级轮盘质量共减轻4.45 kg，达到了预期目标。本优化设计平台为基于轮盘子午面的2维优化平台，可用于轮盘方案阶段的设计工作，为建立更为详细的轮盘3维优化平台奠定基础。

[1]李伦未，陆山.基于ANSYS的多辐板风扇盘结构优化设计技术[J].航空动力学报，2011，26（10）：2245-2250.LI Lunwei，LU Shan.Structure optimum design techniques for multi-web fan disk based on ANSYS[J].Journal of Aerospace Power，2011，26（10）：2245-2250.（in Chinese）

[2]黄致建，郝艳华，郑光华.多级组合盘的整体结构最优化设计[J].航空动力学报，1994，9（3）：245-248.HUANG Zhijian，HAO Yanhua，ZHENG Guanghua.Optimization design of whole construction of multistage disk[J].Journal of Aerospace Power，1994，9（3）：245-248.（in Chinese）

[3]陆山，鲁冯杰.基于ANSYS的整体叶盘结构优化设计[J].航空动力学报，2012，27（6）：1218-1224.LU Shan，LU Fengjie.Structure optimization design for blisk based on ANSYS[J].Journal of Aerospace Power，2012，27（6）：1218-1224.（in Chinese）

[4]章胜，赵明，陆山，等.基于等强度理论的轮盘优化设计方法研究[J].机械科学与技术，2013，32（9）：1322-1326.ZHANG Sheng，ZHAO Ming，LU Shan，et al.Research on an optimal method of disk based on the equivalent strength theory[J].Mechanical Science and Technology for Aerospace Engineering，2013，32（9）：1322-1326.（in Chinese）

[5]Rao A R ，Scanlan J P，Keane A J.Apply multi-objective cost and weight optimization to the initial design of turbine disks[J].Journal of Mechanical Design，2007,129（12）：1303-1310.

[6]李薇，汤禹成，周雄辉.燃气轮机转子轮盘优化设计平台的开发[J].燃气轮机技术，2013，26（1）：27-32.LI Wei，TANG Yucheng，ZHOU Xionghui.Development and application of automatic optimization design platform for gas turbine rotor disk[J].Gas Turbine Technology，2013，26（1）：27-32.（in Chinese）

[7]张乘齐，何爱杰，张卫红，等.基于BOSS平台的热-力耦合场涡轮盘优化设计[J].燃气涡轮试验与研究，2008，21（2）：53-56.ZHANG Chengqi，HE Aijie，ZHANG Weihong，et al.Optimization of turbine disc in heat and strength coupling condition on BOSS platform[J].Gas Turbine Experiment and Research，2008，21 （2）：53-56.（in Chinese）

[8]SONG W B，Andy J K，Rees J.Local shape optimisation of turbine disc firtrees using nurbs[R].AIAA-2002-5486.

[9]Deb K，Pratap A，Agarwal S，et al.A fast and elitist multi-objective genetic Algorithm：NSGA-II[J].IEEETrans.on Evolutionary Computation，2002，6（2）：182-197.

[10]Gutzwiller D P，Turner M G.Rapid low fid elity turbomachinery disk optimization [J].Advances in Engineering Software，2010，41（5）：779-791.

[11]陆山，赵磊.双辐板涡轮盘/榫结构优化设计方法[J].航空动力学报，2014，29（4）：875-880.LU Shan，ZHAO Lei.Structural optimization design method of twin-web turbine disk with tenon[J].Journal of Aerospace Power，2014，29（4）：875-880.（in Chinese）

[12]申秀丽，张野，龙丹，等.涡轮榫接结构多层次设计优化方法[J].航空动力学报，2015，30（12）：2825-2832.SHEN Xiuli，ZHANG Ye，LONG Dan，et al.Multilevel design and optimization of turbine joint structure[J].Journal of Aerospace Power，2015，30（12）：2825-2832.（in Chinese）

[13]Alderson R G，Tani M A，Hill R J.A three-dimensional approach to the optimization of a gas turbine disc and blade attachment[R].AIAA-75-1312.

[14]Mattingly J D，Heiser W H，Pratt D T.Aircraft engine design（2nd edition）[M].Washington：AIAA Education Series，2002：1-719.

[15]Cairo R R，Sargent K A.Twin web disk：a step beyond convention[J].Transaction of the ASME，2002，124：298-302.

[16]陈智，白广忱.涡轮盘结构可靠性与稳健性综合优化设计[J].航空发动机，2012，38（1）：9-12.Chen Zhi，Bai Guangchen.Optimal design of reliability and robustness for turbine disk[J].Aeroengine，2012，38（1）：9-12.（in Chinese）