学生的辨析式说题促发深度学习

福建省厦门市集美区后溪中心小学 林秋缎

在平时的教学中笔者发现随着年龄的增长，学生参与课堂发言的热度持续下降，每节课举手发言的都是“固定的嘉宾”，大部分孩子变成了“观众”。通过多渠道的调查发现这些“观众们”做到变式题就会逊色于积极发言的“嘉宾们”，而且一旦你问他们解题思路或者请说明理由，他们就会“哑口无言”，因而笔者开始了辨析式说题的探究，既然课堂上不敢说那就先从课后开始尝试，给这些“观众们”创设一个辨析式说题的舞台，让他们“敢说”“会说”“想说”。在小学数学课堂教学或课后学习中，辨析说题都是很重要的一种学习方式。所谓理不辩不明，当学生在学习过程中遇到迷惑不解或者含糊不清的知识点时，通过深入辨析说题，可以帮助学生更加深刻的掌握和理解所学知识，从而促发学生们的深度学习。黎加厚教授的理论里提到：深度学习是在理解学习的基础上，学习者能够批判性地学习新的思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的学习情境中，做出决策和解决问题的学习。而辨析式说题就是深度学习的表现形式之一。

通过查阅资料结合农村小学生说题活动的理论基础，并在实际教学时学生说题实践中不断改进，笔者构建了小学数学学生说题活动的一般流程。按照下面的说题流程图来组织学生说题。让学生有依可循。

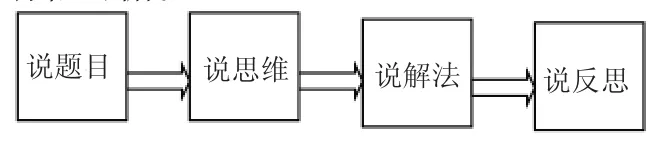
学生说题活动一般步骤

一、典型错例中说题

教师从典型错例中让学生辨析说题入手，这样不仅能知道学生的思维已经“到哪里了”，还可以确定学生“能到哪里”，教师据此才能准确把握学生的困难点，并鼓励学生迎难而上。

例如：一辆小轿车行驶了24千米耗费了2.5升汽油，平均每行驶1千米耗费多少升油?1升汽油可以行驶多少千米?这种题型大部分孩子能答对，但是其中的道理对于学困生而言往往无法厘清，究竟是用路程除以耗油量求平均数，还是用耗油量除以路程求平均数。笔者之前教学中只是鼓励学生比较问题中耗油量和路程的先后位置，再做了一些根据平均数问题找关系式的习题，自认为这样学生的解题思路就能逐渐清晰明白。但是等到这一题的出现，笔者就知道了其实这些原来似乎懂了的学生没有真正的理解耗油量和路程的关系。

根据图象回答问题。

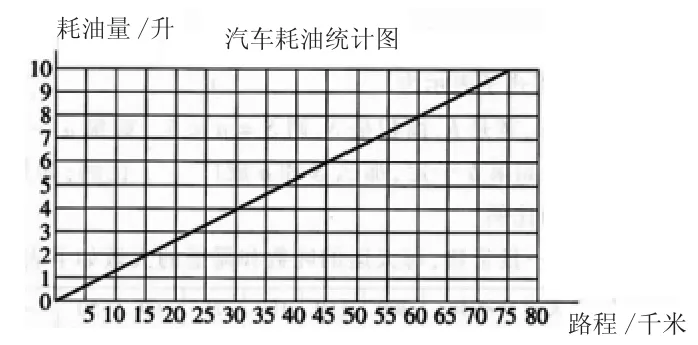
问题：这辆小轿车行驶的路程和耗油量成什么关系？为什么？笔者统计了自己任教的学生的答题情况：全班47人，此题就15人能正确规范的作答。43人知道汽车行驶的路程和耗油量成正比例关系，但是28人错在关系式写错了。此题应该是耗油量随着汽车行驶的路程变化而变化，关系式应该是耗油量÷行驶的路程=平均行驶1千米的耗油量（一定），可学生错写为行驶的路程÷耗油量=平均行驶1千米的耗油量（一定）。正是这题的出现让笔者深受打击，也明白了要让学生从本质上理解就要辨析式说题。

以下是学生的辨析式说题第一说题目：问题是这辆小轿车行驶的路程和耗油量成什么关系？我们从图像能很清楚地看出这是一条从（0，0）出发的无限延伸的射线，从而知道，这两种量成正比例关系。第二说思维：但是此题要联系实际辨析到是耗油量随着汽车行驶的路程变化而变化，因而是耗油量÷行驶的路程，但比值又表示什么量，大部分农村孩子的书面表达很不完善，但是有些学生却懂得从本质意义解释从图中能发现行驶2升汽油走了15千米，那2÷15表示把2升平均分成15份，一份就是平均行驶1千米的耗油量（一定），就能顺利的写出。第三说解法：因为耗油量÷行驶的路程=平均行驶1千米的耗油量（一定），所以这辆小轿车行驶的路程和耗油量成比例关系。当学生能具体用数据说明这个意义就意味着真正的明白了。第四是说反思，当学生说完第三步骤时，教师追问道：“那行驶的路程÷耗油量的比值表示的意义是什么呢？”学生此时有了刚才的说题经验就能很快明白是平均1升汽油能行驶多少千米。再从中让学生反思错解，从而培养学生批判性思维。

课堂上当学生犯错时教师不要慌，要善于营造宽松的气氛，让课堂成为学生尝试解决和辨析错误的主战场，这样学生也能勇敢地跨出第一步——“敢说”，此时辨析式说题也可以引导学生不断纠正错误，促发深度学习。

二、变式对比中说题

变式对比说题就是一题多变，通过实践发现这是提高学生能力的有效策略，这种策略是建立在数学思维灵活多变的基础上，而不是通过反复操练达到的思维的灵活多变，正是学生学习能力和解决问题能力，或者辨析式说题的需要。这种在变式对比中说题的学习深入到内涵与本质上，即本质的解释和数学思想的感悟。

每到六年级总复习总有一类选择题经常出现在练习里，笔者就有意的把它们整合在一起让学生运用辨析式说题的形式，让学生在变式对比中掌握本质，完成深度学习。在复习时采用一题多变、一题多练的策略，学生就不会再出现这类错误。

这4题的选项都是：（ ）

A.第一根长 B.第二根长

C.一样长 D.无法确定

每次遇到这类问题学生的错误率就很高，笔者把这3题归整到一起，让学生用辨析式说题一一分析。学生第一说题目：读完3题后圈画重点后发现题目里的异同点，这四题共同点是和米，不同点是彩带的长度，关键是分清两个分数的差别。第二说思维：第一根用去了它的，用去的是彩带长度的，是一个分率，用彩带的长度乘，第二根用去了米，是一个具体的数量用彩带的长度减。学生的说题中能明确地说清这一点就能以不变应万变了。第三说解法：第一题选D，因为彩带的长度未知，会出现第一根长、第二根长或一样长的结果，所以选D，第二题选B，因为第一根剩2-2×=（米），第二根剩2-=1（米），第三题选A，第一次是用全长×，第二根是剩下的长度×，此题单位“1”。第四说反思：此题关键是分清两个分数的差别：第一个是一个分率，第二个是米，是一个具体的数量。

在学完百分数后笔者就有意把①商店同时售出两双皮鞋，每双成本价都是200元，其中一双赚25%，另一双亏了25%，同时售出两双鞋，是盈利了还是亏损了？②商店同时售出两套童装，售价都是120元，一套是盈利25%，另一套亏本25%，这家童装店卖出的这两套童装总体盈利了还是亏损了？说说理由？

从学生的说题中发现，读完题目学生能一眼发现两题的第一条数学信息有区别，第一题是已知成本价，第二题是已知售价；在说思维环节中要理解盈利25%和亏损25%都是和原价比，那这两题就能转化成“求比一个数多（或少）的百分之几是多少？”以及“已知比一个数多（或少）的百分之几是多少求这个数”的数学模型，接着说解法，学生能清楚知道第一题要用乘法解决分别算出售价，而第二小题要用除法算出成本价在进行比较。最后说反思就是沟通两题的联系和检验了。

以上是关于“数与代数”模块的变式说题，那么在“图形与几何”领域呢？当然也可以采用变式说题。比如，在教学小学数学五年级《三角形的面积》时，可以让学生这样说题：

一个平行四边形的面积是16平方厘米，与它等底等高的三角形的面积是（）平方厘米。（学生很快就求出来是8平方厘米。）

变式题1：一个平行四边形的面积是16平方厘米，从这个平行四边形中剪出一个最大的三角形，这个三角形的面积是（ ）平方厘米。

（请学生边画边说他是怎么剪的，有多少种剪法？）

变式题2：剪完后，剩下部分的面积是（ ）平方厘米。

通过这样层层递进的3道练习，变中有不变，提高学生思维的灵活性和广阔性。对待当前国家推行的“双减”政策，减量不减质，课上选准例题，课后采用一题多变，让学生变式说题，并引导学生在说题中总结解题特征、解题方法，以不变应万变。这样不但能够帮助学生巩固有关的基本概念，掌握各种题型的解题方法和技巧，而且帮助学生学会把平时所学的知识归纳整理，学会同中求异、异中求同。有助于培养学生抽象概括能力，完成由例及类的学习，大大简化了学习环节，真正实现减负提质。

三、问题驱使中说题

小学生的辨析、辩论能力还处在初步发展阶段，特别是农村的孩子，这方面的能力尤其薄弱，教师只有从学生学情和年龄特征出发，在教学新知的教学中，教师有意识地培养学生的辨析能力，准确的把握教学中的辨析点，抓住教学中辨析价值的问题，通过对这些问题的辨析，达到厘清概念，在新知学习中辨析说题是内在思维活动，在问题的驱使下让学生辨析说题。

以“圆锥的体积变化”为例，在学习完“圆锥的体积”之后，笔者设计了以下几个问题让学生从辨析说题过程中提升圆锥体积问题的解决能力。让不同层次的学生根据自己的能力选择说题，教学环节：

问1：通过昨天的学习我们学习了圆锥的体积推导，那要使三角形旋转成圆锥，必须是什么三角形？以哪条边为轴旋转？

生：只能是直角三角形，以一条直角边为轴，另一条直角边为底面半径。有两种情况，如图：

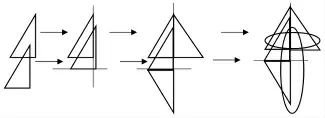
问2：以哪条边为轴，圆锥的体积更大，为什么？

生：通过圆柱体积的学习，我们知道在侧面积相同的情况下，圆柱的底面半径越长，圆柱的体积就越大，从而我们可以得出，在同样是这张三角形的纸张里，底面半径越大的情况下，圆锥的体积就会越大。

问3：如果这个直角三角形的一条直角边为4厘米，一条直角边为3厘米，那这两个立体图形的体积是多少呢？

小结：以较长的直角边为半径得到的圆锥体积更大。

问4：如果是以斜边为轴旋转，会形成什么图形呢？

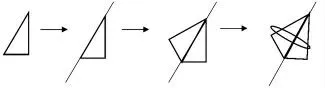
生：那就形成了两个底面一样的圆锥的组合图形。（学生边画图边解说。）

问5：这个直角三角形的一条直角边为4，一条直角边为3，斜边为5，你能求出它的体积吗？

生1：要通过三角形的面积求出斜边对应的高也就是圆锥的底面半径，再设上面圆锥的高为h厘米，而下面那个圆锥的高是（5-h）厘米。最后利用圆锥的体积公式求取。

生2：这个组合图形中的两个圆锥的底面积是一样的，也可以把两个圆锥的体积转化成一个高是5厘米，底面半径是2.4厘米的圆锥的体积。

问6：从上图的结果，你觉得它相当于一个怎样的圆锥？

小结：它相当于上下两个圆锥等底面，两部分的高可以融合的圆锥。

其实以斜边为轴的立体图形的体积计算，难度较大，但是通过6个问题细化了难度，给学生提供了思路，有利于培养学生的数学思维还能培养学生用草图去分析的应用和能力。郭华教授指出深度学习是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与体验，成功获得发展的有意义的学习过程。在问题驱使中说题深在过程和方法中，即知识的过程方法和学习的过程方法。

语言是思维的外壳，学生在辨析式说题的过程中，语言与思维的交替和融合促进了二者的协调发展。让学生辨析式说题既能说出对问题的理解、教材知识，又能说出心中的困惑、答题的思维过程，其他学生在聆听他们分析的过程中，更容易吸取他们的观点，并内化为自身的解题能力。