基于卡方距离度量学习的面部表情识别算法

秦 毅，赵二刚

(1.重庆电子工程职业学院 人工智能与大数据学院，重庆 401331； 2.南开大学 电子信息与光学工程学院，天津 300071)

0 引 言

面部表情识别(facial expression recognition，FER)作为一个活跃的多学科研究领域，在转录视频、电影或广告推荐、远程医疗中的疼痛检测等领域具有广泛的应用潜力[1,2]。

根据从图像中提取面部表情特征的不同，可以将现有的FER方法分为基于几何特征[3]和外观特征的方法[4]两类方法。文献[5]提出一种基于外观特征进行面部识别的方法，该方法采用Viola-Jones框架提取面部表情感兴趣区域的局部二值模式图像，利用卷积神经网络识别结果。文献[6]提出了一种基于几何特征的面部识别方法，该方法利用面部特征点来确定面部特征间的相对距离，以便捕获不同表情下的面部肌肉运动形态，然后使用面部特征点间的相对距离来训练网络，提高分类模型的辨别能力。文献[7]提出了一种新的特征提取技术，该技术使用压缩感测技术将提取的特征变换为高斯空间，在降低特征向量维数的同时，将特征向量与分量支持向量机的径向基函数核匹配，从而可以对任何向量进行分类。文献[8]提出了一种利用局部人脸区域识别面部表情的方法，该方法对每个局部区域采用类成对的中级描述符来提取中级特征和Adaboost特征选择用以选择更多的判别特征，在野外面部表情识别中提高了准确率。文献[9]提出了一种基于孤岛损失来增强深度学习特征判别力的方法，该方法采用减少类内变化，同时扩大类间差异的方式提高野外面部表情识别的准确率。

野外面部表情图像识别具有各种挑战，如自发情绪和光照变化等，使得大多数FER方法不能有效识别。此外，在不受控制的条件下的面部表情识别也是一个尚未解决的问题。针对上述问题，提出了一种基于局部卡方距离的KNN算法，用于人脸的表情识别。首先定义了计算卡方距离的新公式；其次，在优化算法中引入了Dropout技术用于解决过拟合现象；最后，使用KNN算法进行表情识别。此外，所提出的损失函数使用了卡方距离，从而进一步改善所提方法的识别准确率。

1 K最近邻算法

K最近邻(k-nearest neighbor，KNN)算法是近年来新兴的分类方法之一，它在训练大数据集的同时，具有资源利用有限的优点。KNN是一种无监督学习分类算法，也是应用最广泛的非参数模式分类方法之一，它降低了对概率密度复杂性的关注。KNN算法通过在K个最近的邻居样本标签来对目标样本进行分类。KNN算法在分类问题和回归问题中具有广泛的应用空间。

在KNN算法中，影响结果的主要是K值和距离，因此使用KNN算法解决分类或回归问题时，需要重点关注K值的优化和合适的距离度量方法。若K取值太小时，样本的分类结果取决于最近的样本类别，容易受到噪声点的影响；若K取值太小时，样本的分类结果容易受到不平衡数据集的影响，导致分类模糊。因此，在使用过程中，选择K值从1开始逐步增大，使用交叉验证来评估不同K值下的分类情况，选择最优K值。

距离度量则是衡量样本之间的距离，当两个样本之间的距离越小，说明两者的相似度越大，同属一类别的概率也就越大。常用的距离的度量方法有欧几里得距离和马哈拉诺比斯距离。欧氏距离是指空间中两点之间的绝对距离，定义为

(1)

式中：xi和xj为样本点。欧氏距离在多数情况下只能对低维空间中超球状分布的数据有效，容易受到数据集中噪声的干扰。

马氏距离表示数据的协方差距离，该度量是计算样本属性标准化之后的距离，其定义为

(2)

式中：S表示样本xi和xj的协方差。马氏距离对数据集中呈超椭球型分布的数据有效。

下面给出KNN算法的计算步骤：

(1)初始化K值；

(2)计算目标数据与带标签数据之间的距离；

(3)按照距离远近进行升序排序；

(4)选取与当前目标数据最近的K个点；

(5)选择K个点出现最多的类别进行新样本分类。

2 基于卡方距离度量的面部表情识别

在过去的十年中，人们对度量学习进行了许多研究。度量学习的目标是利用训练集的信息改进数据比较度量。现有的方法大多集中在马氏距离度量学习上。然而，在人脸表情识别中广泛使用的特征往往是基于直方图的图像纹理描述，而马氏距离无法准确描述该空间中数据之间的关系。卡方距离是直方图数据比较中最著名的方法。因此，本文提出了一种基于卡方距离KNN的表情识别方法，其算法流程如图1所示。

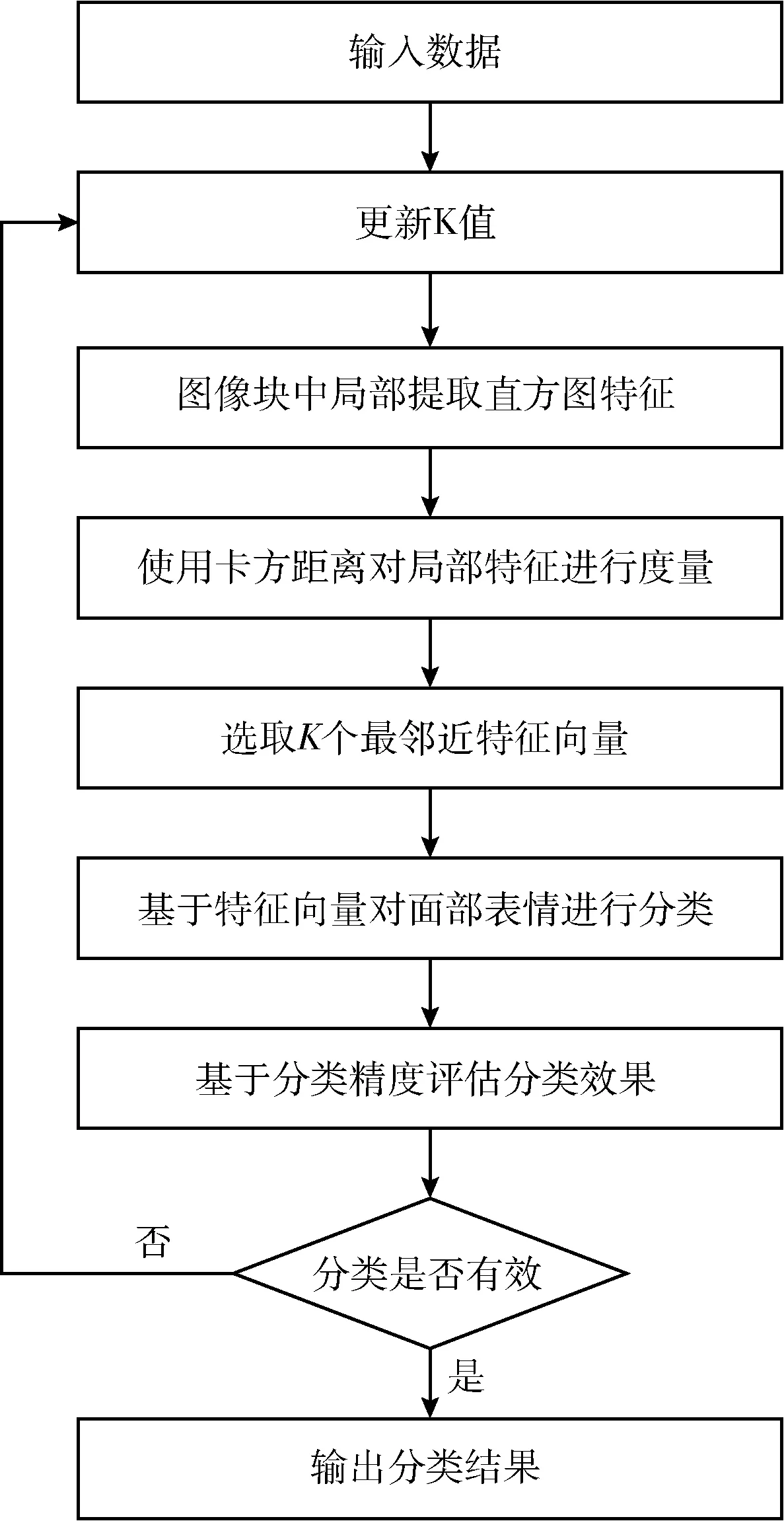
图1 所提方法的流程

2.1 基于卡方距离度量的KNN

距离度量学习(distance metric learning，DML)也称为相似度学习，其目的是为了衡量样本之间的相近程度，DML通过特征变换得到特征子空间，然后使用度量学习，让类似的目标距离更近，不同的目标距离更远。DML经常应用于大量的机器学习方法中，如K近邻、支持向量机、径向基函数网络等分类方法以及K-means聚类方法。

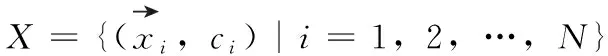
(3)

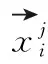
(4)

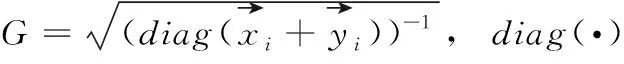
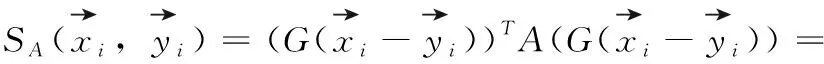
(5)

(6)

基于卡方距离度量的损失函数为

(7)

2.2 基于随机梯度下降卡方距离度量

基于卡方度量的KNN分类时需要对训练数据中获取每个训练数据的K近邻先验知识，然后根据损失函数对训练误差进行最小化处理，求解映射矩阵L。由于基于卡方距离度量的损失函数在L矩阵的元素中是非凸的，因此，使用诸如梯度下降之类的方法来最小化成本函数时，需要对矩阵L的初始值进行优化，而且存在陷入局部最小值的问题。本文通过半正定规划(semi-definite programming，SDP)克服陷入局部最小值的问题。SDP作为线性规划的一种扩展，通过约束矩阵的半正定性实现求解优化问题，常用于实际问题的凸优化求解，SDP可描述为

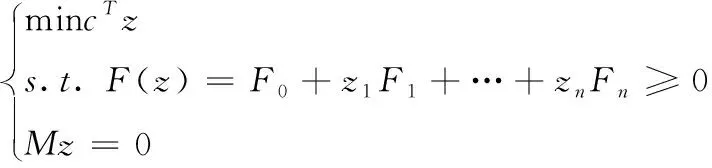
(8)

其中，F0,F1,…,Fn表示对称矩阵(k阶)。

在SDP中，通过结合矩阵的半正定约束来完成优化。基于卡方距离度量的优化问题可以表示为

(9)

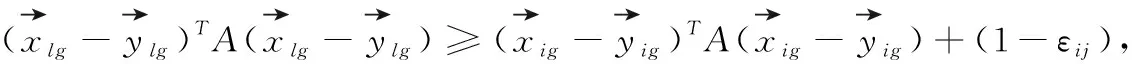
(10)

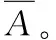
Frobenius范数是度量学习中流行的正则化算子，用于避免过度拟合训练数据。Frobenius规范的度量学习问题的标准形式定义为

(11)

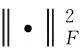
(12)

在Dropout技术中，如果p(φij=0)=α，则有

(13)

由于Frobenius范数只能简单地以相同的方式约束学习矩阵的所有元素，无法对学习矩阵的对角元素做特殊处理。且在学习矩阵中，对角元素描述了每个特征的重要性，其余元素描述了特征的相互作用，因此对角元素相对于其它元素更重要。本文提出了一种针对学习矩阵的对角线和非对角线元素Dropout正则化方法。

假定Φ为随机矩阵，其对角元素和非对角元素分布服从 [0,0.5] 和 [0,1] 之间的均匀分布， [0,0.5] 上的累积分布函数可以表示为

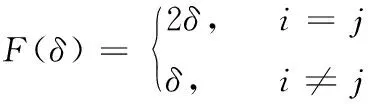
(14)

基于矩阵Φ，Dropout方法在0≤δ≤0.5的概率定义为

p(φij=0)=p(Φij≤δ)=F(δ)

(15)

因此

(16)

根据式(11)优化问题可以修改为

(17)

从上式可以看出，利用Frobenius范数和L1范数对矩阵A进行了正则化。因此，矩阵A的对角元素在Frobenius范数和L1范数正则化器中都有贡献，其余元素仅在Frobenius范数中有所贡献。

2.3 基于局部的卡方度量表情识别方法

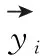
(18)

根据特征向量的维数，学习矩阵A是D×D方阵，包含U×U个图像块。为了在每个图像块中执行单独学习，可以在矩阵A的相应块上采用求解距离度量问题的dropout正则化方法。对于第U个图像块，对应矩阵A的第U个对角块。其特征是为每个图像块训练数据

(19)

因此，输入数据的维数减少到k，每个块的学习矩阵是k×k。 局部度量学习如算法1所示。

算法1：局部度量学习用于人脸表情识别

(1)输入： 训练数据Y， 步长γ；

(2)迭代A0←0，A0∈RD×D(包含U×U个子块)和T；

(4) 当前子区域特征：Yu；

(5) 使用dropout正则化的度量学习在Yu上训练Au；

(6) ∏psd(At)；

(7) endfor

(8) 返回A

在所有局部矩阵学习后，两个人脸图像的特征距离可以利用式(20)计算

(20)

由于矩阵A的非对角块为零，因此，式(20)可重写为仅为非零块计算的距离之和

(21)

如果正确地学习对角线块，那么将最小化来自类似类的两个图像块与块之间的特征距离；而对于来自不同类的图像，将最大化这些特征距离。由于图像的块与块的特征距离在数学上是正的且彼此独立，因此这些值的总和对于来自同一类的数据是最小的，来自不同类的数据是最大的。

本文提出的基于局部卡方距离的KNN表情识别方法体现了特征量之间的相对关系，对每个特征量赋予相同的权重，但是不同特征对分类的贡献并不同，在局部卡方度量的表情识别方法上，引入特征权重系数，对不同的特征赋予不同的权重。

针对局部卡方距离识别方法中错误样本数量为n， 之后去除第p,p=1,2,…m个特征量，使用局部卡方度量的KNN方法对测试样本进行识别，得到错误样本数量为np。 计算vp=np/n， 该值越大说明分类误差越大，反映了第p个特征量对分类的贡献就越大,反之亦然。则第p个特征权重系数可定义为

(22)

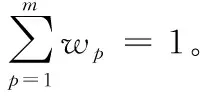
3 实验结果与分析

为了验证所提算法的有效性，采用FER研究领域公开可用的受控环境下和非受控环境下的数据集进行面部表情识别的各种实验，用于评估所提出的度量学习算法中卡方距离、特征提取补丁大小、局部学习和正则化器的贡献度，并且将获得的结果与现有方法进行比较。所有实验均在配置为CPU Intel Core i7-4700MQ @2.4 GHz，RAM 8 GB，Windows10环境下的机器中执行。

3.1 数据集

本文选取扩展Cohn-Kanade(CK+)数据集、野外的静态面部表情(SFEW)数据集和大型的面部表情数据库RAF-DB这3个数据集用于测试。下面给出几个数据集的详细信息。

CK+数据集是在实验室控制条件下获得的图像，这个数据集由来自123个受试者的593个图像序列组成，其中327个序列具有包含6个基本情感和蔑视的面部表情标签。在发布的数据集中，使用活动外观模型定位了68个面部界标点。每个图像序列从中性面开始到其表达标签的峰值。在本文中，选择327个标记序列的最终峰帧用于评估所提出的算法。

SFEW 2.0为在野外(非控制)场景下获得的自然表情的图像，由一组光照、头部姿势等存在巨大变化的静态图像组成。该数据集分为训练、验证和测试3个图像子集，图像数量分别为958、436和372，其中，培训和验证集的标签可供研究人员公开使用。在本文针对SFEW数据集的所有实验中，训练和验证集分别用于训练和测试阶段。

RAF-DB数据集包含了从互联网上下载的29 672张不受控制的面部图像，共有315个学习注释器对该数据集中的每个图像进行了大约40次标记。除了基本情绪外，该数据集还包含11种复合情绪，因此，这是尝试提供在不受控制的条件下具有复合情绪的大规模面部表情识别数据库。在数据集中的每个图像旁边还发布了面部边界框，5个手动注释的面部界标点，37个自动界标点。在训练集和测试集中，包括6种基本情绪和中性情绪等7类情绪，分别有12 271幅和3068幅。本文利用RAF-DB在一个大规模人脸表情识别数据集上对该算法的可扩展性进行了评估。

3.2 对比研究

通过进行各种实验来评估所选择的距离，特征提取补丁大小，局部学习和正则化器在所提出的度量学习算法中的效果。首先在基于不同直方图特征的人脸表情识别算法中，将运用卡方距离、马哈拉诺比距离以及KNN和SVM分类器的识别结果进行了比较。其次，将不同的补丁大小用于特征提取，以探索此参数对所提出算法的影响。然后，将所提出的局部度量学习与全局度量学习的结果进行对比。最后，执行所提出的度量学习采用不同正则化器的测试。

3.2.1 度量距离对比

为了验证卡方度量距离的优越性，对现有3类直方图特征LBP-LPQ[10]、HWP[11]和CA-LBFL[12]应用不同的度量距离，并对测试结果进行对比。提取特征的分类方法有4种：基于欧式距离的KNN分类、基于一对一的RBF核的SVM分类、基于马哈拉诺比距离的KNN分类和基于提出的卡方距离度量学习的KNN分类。在这些实验中，对于KNN分类器，K设置为7。评价方法采用独立的10倍交叉验证各种分类方法。在验证方案中，图像随机分成10组，图像数量大致相等。其中一组作为实验组，其余9组作为训练组。此过程重复10次，以使每个组都会充当测试集。

图2和图3为不同数据集上的识别率实验结果，从图中可以看出，本文提出的基于卡方距离识别人脸表情的算法比其它方式更优，对这些特征描述符进行度量学习时更有效。

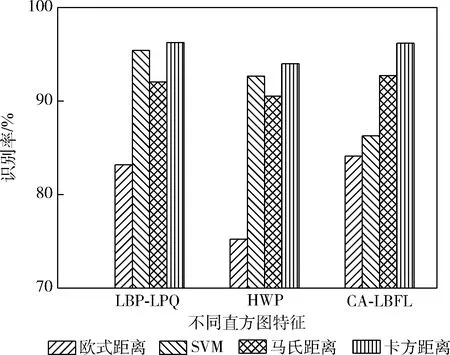
图2 不同度量距离在CK+数据集的识别率

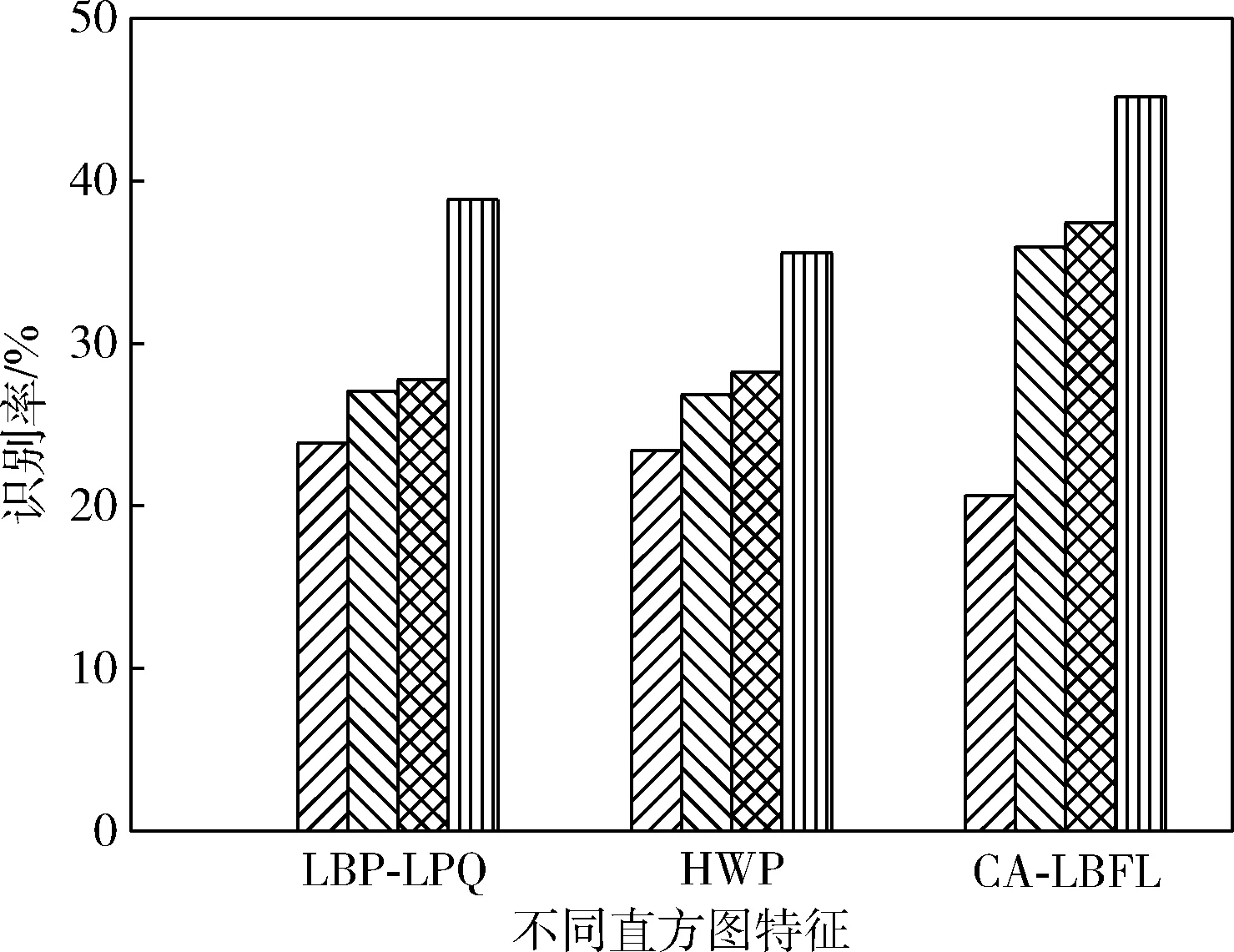
图3 不同度量距离在SFEW数据集的识别率

3.2.2 补丁大小的影响

为了评估算法1在所提算法中的贡献度，使用尺寸为2×2～8×8等不同大小的补丁进行实验。对于每个分区，首先从图像块中局部提取直方图特征；其次，将提取的局部特征串接成最终的特征向量；然后，使用算法1学习所提出的度量；最后，利用基于卡平方度量的KNN分类器进行分类。在特征提取方面，采用了LBP-LPQ、HWP和CA-LBFL等多种方法。该实验过程在CK+和SFEW数据集上执行。对于CK+数据集，使用独立的10倍交叉验证方案，而SFEW数据集则将训练集和验证集分别用作训练集和测试集。图4和图5给出了实验结果。

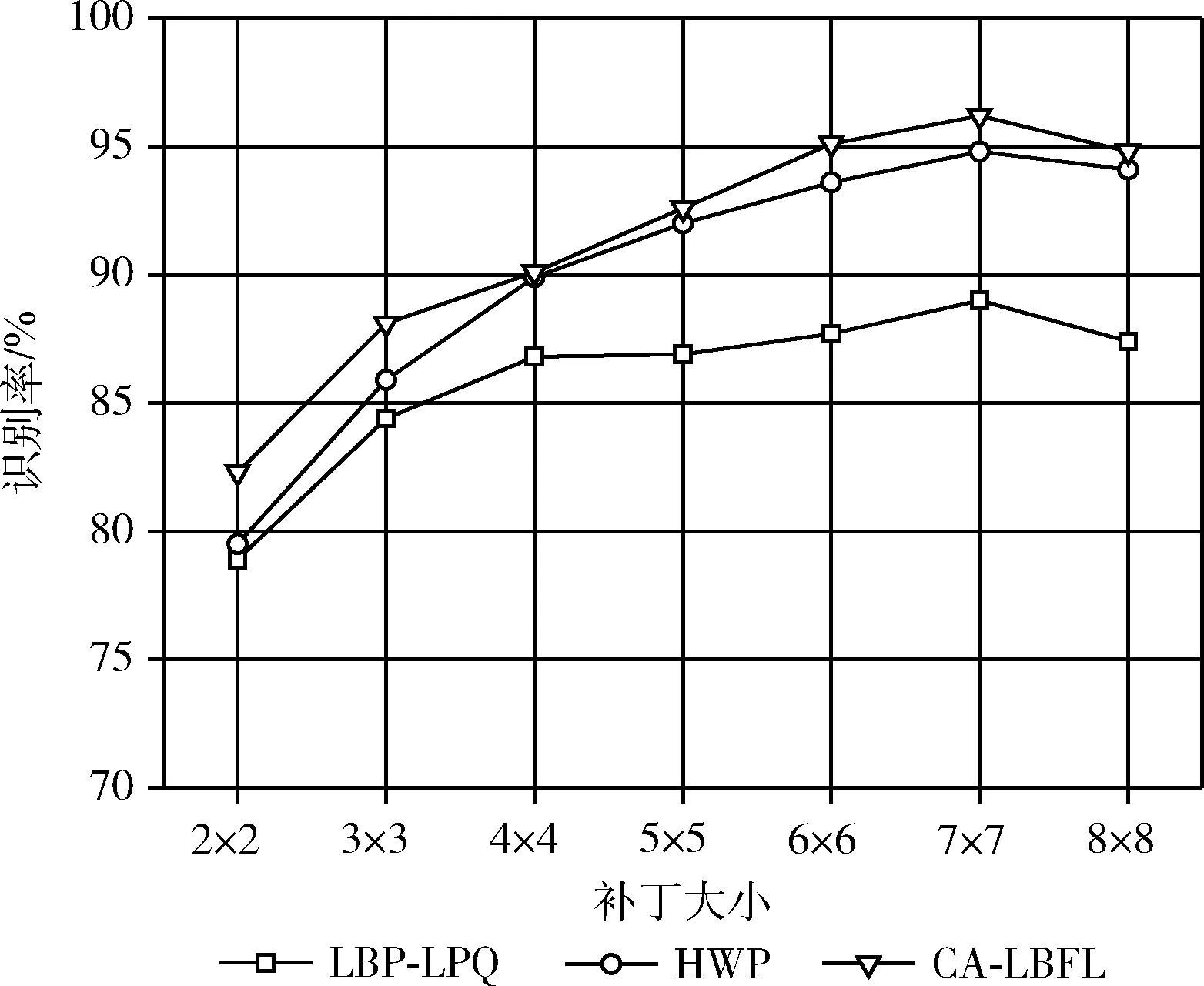
图4 CK+数据集中使用不同补丁时的识别率

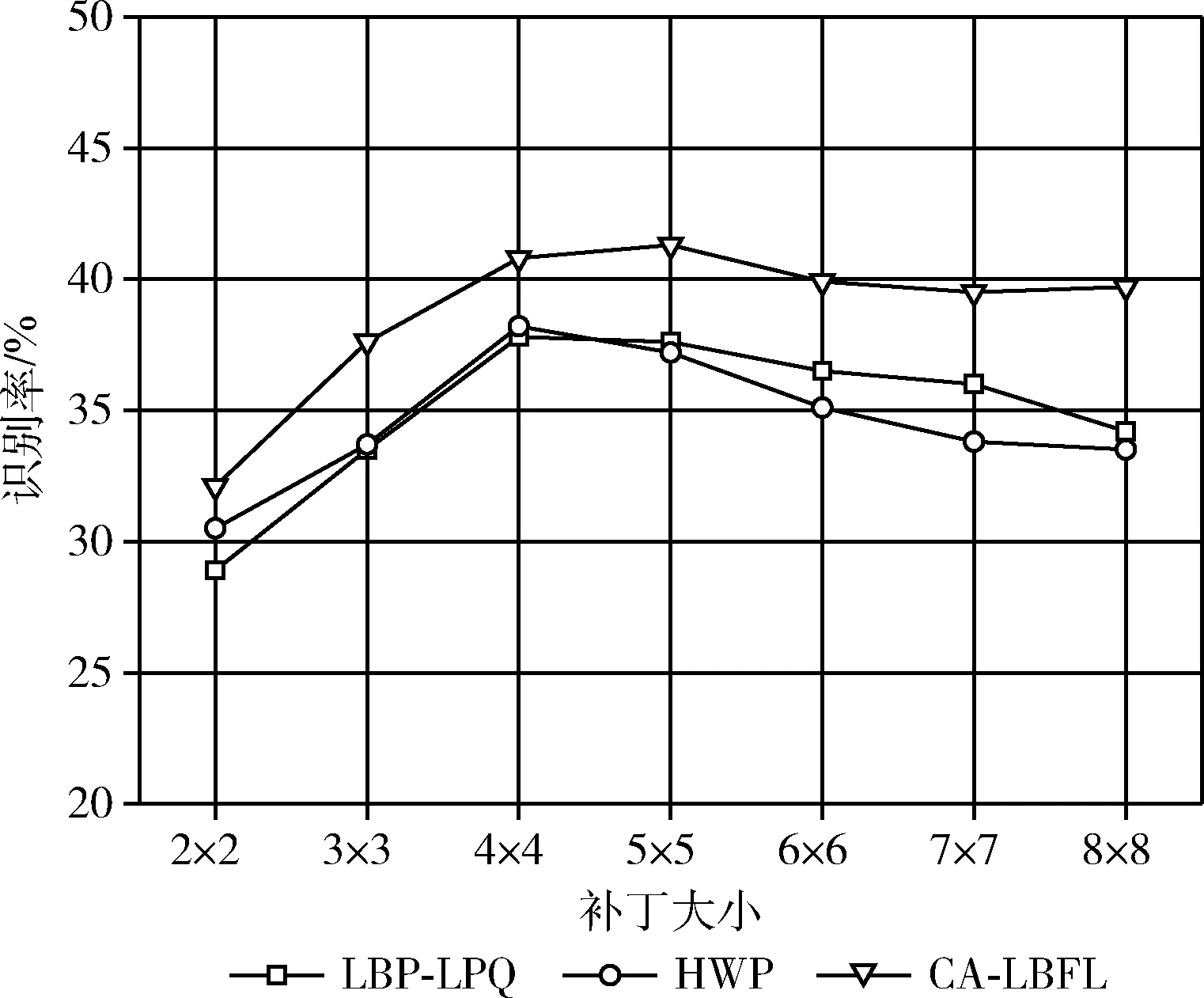
图5 SFEW数据集中使用不同补丁时的识别率

从图4中可以看出，CK+数据集的总体准确性随补丁数量的增加而近似增加。这可能是由于在最终特征向量中，尺寸很小的补丁无法正确地表示面部图像的足够信息，而当补丁数量增加时，特征向量包含更多的局部信息。因此，当补丁尺寸提高到6×6时，识别率最高。同理，从图5中看到，SFEW数据集的识别率随着增大到4×4获得最高。但是，当补丁的尺寸继续增加时识别率呈现降低的趋势。这可能是由于数据集中较大的头部姿势引起的。大头姿势时，小补丁的效率会大大降低。因此，数据集上的识别率会随着补丁数量的增加而降低。为了在计算成本和准确性之间进行权衡取舍，对于CK+和SFEW数据集，本文之后的实验分别选择了6×6和4×4的补丁尺寸进行测试。

3.2.3 局部与全局学习对比

为了探索基于卡方距离度量的局部学习在面部表情识别中的效率，进行全局和局部学习。在全局学习中，将提取的特征进行整体学习。在局部学习中，分别对每个图像块执行学习过程，最后进行权重调整。表1中显示了使用基于不同特征的两种方法的识别率。从该表中可以看出，应用于不同提取方法的局部度量学习在CK+、SFEW数据集上的测试结果明显优于全局度量学习。

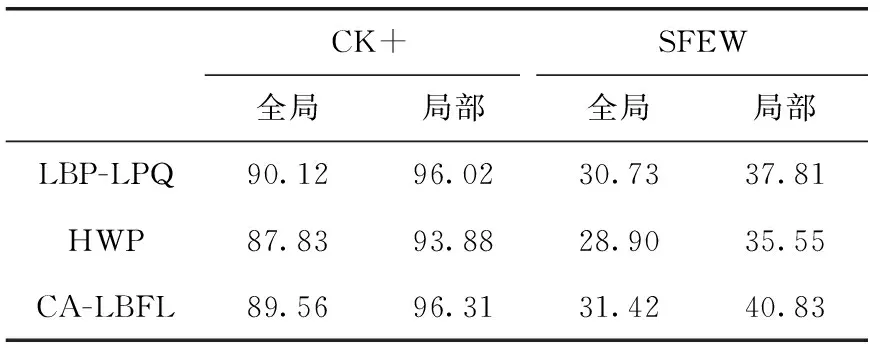
表1 全局和局部度量学习的测试结果

3.2.4 正则化器对比

为了避免过度拟合训练数据，本文提出了基于Dropout的正则化器，下面需要评估该技术的效率。为此，在所提出的面部表情识别的局部度量学习方法中定义并使用3种变体：没有正则化器、Frobenius Dropout正则化、结构化Dropout正则化。采用SFEW数据集对这3类不同正则化进行测试，测试结果如图6所示。

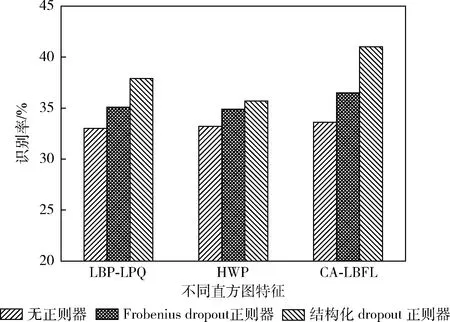
图6 不同正则化器在SFEW数据集的测试结果

从图6中可以看出，相对于不使用Dropout技术的情况，采用Frobenius Dropout正则化的识别率提高了约0.5%～3%，结构化Dropout正则化提高了大约3.4%～7.6%。实验结果表明，所提出的正则化增加了度量学习算法对测试数据的通用性。

3.3 实验结果

为了验证提出方法的分类效果，本文采用LBP、LPQ、HOG和POEM这4个直方图特征组合的方式在CK+、SFEW和RAF-DB数据集上进行分类测试，获得的分类混淆矩阵结果见表2、表3、表4。从表中可以看出，对于CK+数据集，提出的方法能够完全识别高兴、惊讶两种表情，在7种表情中厌恶表情的识别率也很高，排名第三；对于SFEW数据集，识别率最高的表情为愤怒，在6种表情中排名第二、三位的表情为惊讶和高兴；对于RAF-DB数据集，识别率最高的表情为惊讶，在7种表情中排名第二、三位的表情为高兴和愤怒。

表2 CK+数据集生成的混淆矩阵

为了验证提出方法的优越性，本文比较了不同的最新的人脸表情识别方法：IL-CNN[9]、IACNN[13]、DLP-CNN[14]和SJMT[15]。表5给出了本文方法与其余方法在CK+、SFEW和RAF-DB数据集的测试对比结果。从表5中可以看出，所提出的算法比其它算法更准确，不同外观特征直方图的组合以及所提出的度量学习方法有效地提高了面部表情识别准确度。

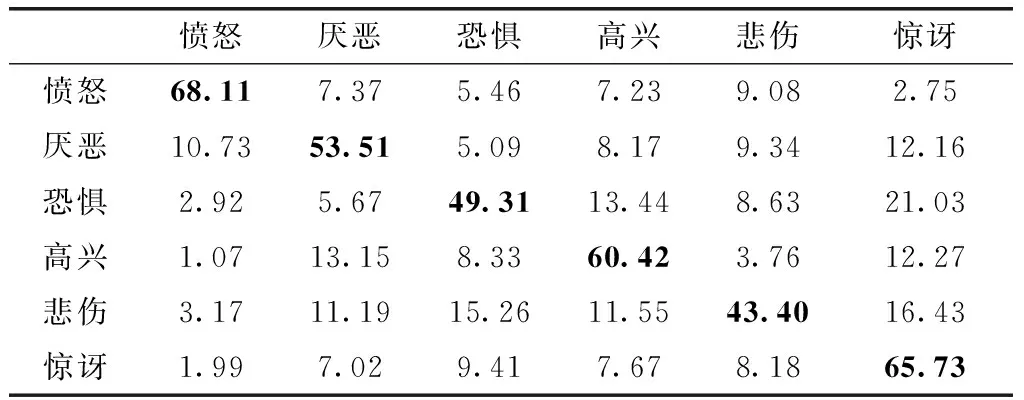
表3 SFEW数据集生成的混淆矩阵

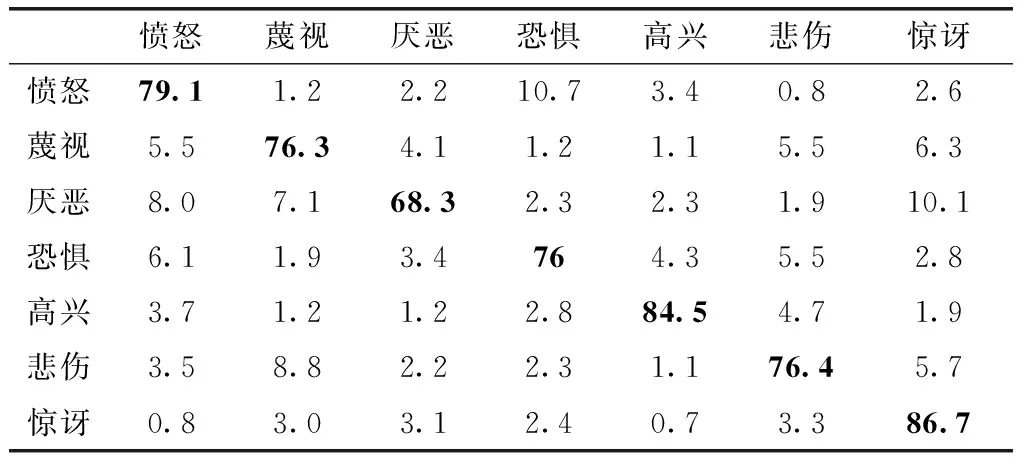
表4 RAF-DB数据集生成的混淆矩阵

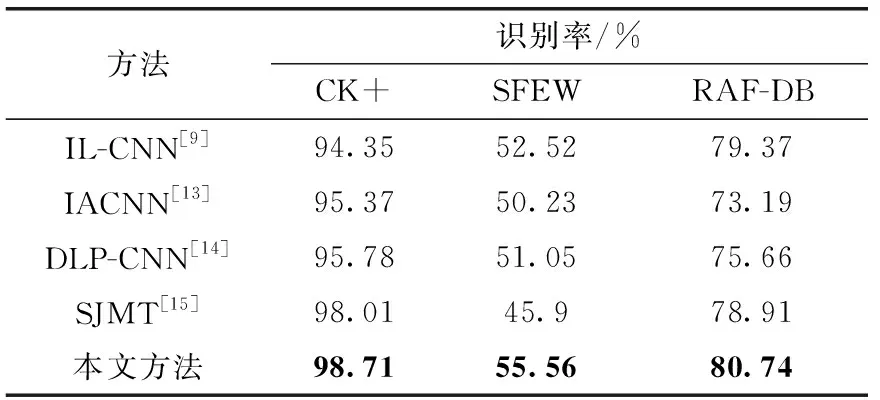
表5 不同人脸表情识别方法的识别率

4 结束语

本文提出了一种基于卡方距离度量学习的面部表情识别算法，用于解决野外复杂环境下面部表情面临的头部姿势变化、光照变化等挑战。提出的方法采用基于卡方距离方法进行KNN分类，利用SDP方法将损失函数修正为凸优化，同时将Dropout技术引入度量学习防止训练数据出现过拟合现象，最后引入权重系数，提高识别准确性。实验结果表明，提出的算法提高了不受控环境下的面部表情识别率。