基于WFKP聚类算法的培养质量评估

张德珍，赵文波，高 鹏

(1.大连海事大学 信息科学技术学院，辽宁 大连 116026； 2.大连大学 经济管理学院，辽宁 大连 116026)

0 引 言

传统的培养质量评估方法如AHP模糊评价法[1]、灰色度评价法[2]，面对海量信息时效率低下、主观性过强，存在着一定的局限性。基于聚类分析与培养质量评估在目的上的一致性，将聚类算法加以改进后应用于培养质量评估，有着较高的实用价值。文献[3]通过引入小生境和禁忌算法思想，提高了算法的抗干扰性和聚类精度；文献[4]使用线性拟合来自动选取初始簇中心，文献[5]融合遗传算法来选取初始簇中心，减少了初始簇中心选取不当对聚类稳定性的影响，但遗传演变中的适应度函数不易设计，算法计算成本高昂；文献[6]使用低密度区域来划分高密度区域，适用于任意簇分布的聚类问题，但对实际应用中高维数据分布不均时聚类辨识能力偏低，准确率不高。以上聚类算法集中于对最佳聚类数目或初始簇中心的改进，只适用于数值属性，无法处理培养质量评估中的分类属性。FKP算法[7]使用海明距离处理分类属性的特征差异，并引入了隶属度的概念使其具备软划分的能力。但针对于培养质量评估，FKP算法未能考虑到样本的总体差异和不同特征的权重差异，直接将其应用于培养质量评估会降低聚类准确性，不能达到最佳聚类效果。

针对上述问题，本文在FKP算法的基础上，提出一种面向混合属性的特征加权WFKP聚类算法。首先提出一种改进的分类属性相异度计算公式，综合考虑簇中所有样本的整体差异，提高对样本相似度的区分能力。然后在K近邻算法[8]和MI(mutual information)的基础上，在聚类中引入样本数值特征和分类特征的权重分析，提高了聚类算法的准确率。最后通过UCI数据集验证算法的有效性，并对某高校的培养质量数据集进行聚类分析，降低培养质量评估的工作量和复杂度，实现评估过程的智能化、规模化和精准化。

1 FKP聚类算法

FKP算法的基本思想是从样本集中随机选取k个样本作为初始簇中心，计算各个样本与初始簇中心的距离，将样本对象划分到距离最近的簇中，然后更新簇中心并不断迭代此过程，最终簇中心的波动范围小于指定的阈值时聚类结束。下面给出FKP聚类算法中的相关定义。

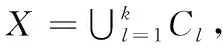
定义1 相异度：相异度表示两个对象差异程度的数值度量，聚类的难点在于准确量化样本xi和xj的相异度。FKP聚类算法中样本xi和xj的相异度定义如下

(1)

式(1)的前半部分采用欧氏距离计算样本的连续属性的相异度，后半部分采用海明距离来表示离散属性的相异度，欧式距离的定义如下

(2)

海明距离的定义如下

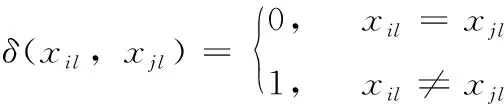
(3)

定义2 隶属度：样本xi属于簇Cj的模糊程度定义为uij。 由于培养质量评估的指标众多，部分指标具有模糊性和不确定性，不能把样本严格地划分到某个簇中，故应引入模糊集理论，考虑量化样本间的模糊关系，从而准确客观地描述样本的分布特征，由Lagrange乘数法计算uij，uij的计算过程如下

(4)

定义3 目标函数：FKP算法的优化目标是簇间样本相似程度最小化，簇内样本相似程度最大化，即最小化所有样本到簇中心的平方误差和SSE(sum of squares due to error)，FKP算法的目标函数E(U,C) 如下

(5)

式中：k为聚类个数，U为n×k的模糊划分矩阵，uij表示第i个样本隶属于簇Cj的模糊程度；ded(xi,cj) 为样本xi与簇中心cj的数值属性的相异度，δ(xi,cj) 为样本xi与簇中心cj分类属性的相异度；模糊因子α控制聚类的模糊程度，比例系数γ调节连续属性和离散属性的权值比例。

目标函数受限于以下约束条件

(6)

2 WFKP聚类算法的设计

针对海明距离忽略样本特征关联而导致的信息缺失问题，本文提出了一种改进的分类属性相异性度量方式，在马氏距离的计算中引入比例系数，改进协方差矩阵估计，降低高维数据集下对样本数据的误分率，用改进的相异度计算方法寻找样本的K个近邻点，用于样本特征的权值分析。

2.1 分类属性相异度改进

马氏距离是基于样本分布信息的一种无量纲距离，考虑到样本的特征关联，克服了海明距离的缺陷。

样本的分布信息由协方差矩阵来刻画，样本xi与簇中心cj的马氏距离定义如下

(7)

其中， ∑是样本分布的协方差矩阵，是一个对称的正定矩阵。协方差矩阵的计算是求解马氏距离的关键，传统的协方差矩阵计算方式如下

(8)

式(8)中用当前聚类下数据的样本分布来作为马氏距离的协方差矩阵，由于聚类前期簇中心位置改变较大，样本分布不稳定，上述计算方法会导致较大的估计误差进而降低算法的稳定性。为此我们增加了聚类中已分类样本和未分类样本的概率统计，引入了比例系数Φ，其定义如下

(9)

γ=1-|Cl|/|Clij|

(10)

式(10)中， |Cl| 是簇Cl中已有样本的个数， |Clij| 是待分类样本xi的第j个属性值在簇Cl中出现的频率。

∑为正定矩阵，根据矩阵理论，对其进行如下分解

(11)

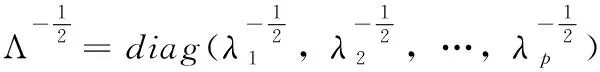
(12)

2.2 数值属性的权值计算

对于数值属性的权值分析，文献[9]采用粒子群的方法先将数值属性离散化，但其离散过程具有较强主观性。文献[10]使用信息论来分析权值，这需要知道数值属性的概率分布，培养质量数值属性相互关联且可能存在冗余，其概率分布不易获得。本文利用改进的相异度寻找簇中心的K近邻样本，在此基础上定义培养质量数据样本的簇内离散度和簇间离散度，来计算数值属性的权值。

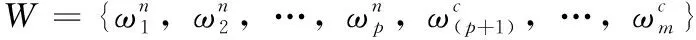
Neark(xi) 是式(12)下得到的距离样本xi最近的第K个样本点，xi的K近邻样本定义如下

(13)

定义4 簇内离散度distinter， 表示簇Ck内的各数据对象的数值属性Aj与此属性的均值μjk的离散程度。从样本集X随机抽取样本xi， 利用式(13)在与xi同类的簇内寻找xi的同类K近邻样本，记为Near_interj,j=1,2,…,k。 样本xi与Near_interj在特征Al上的差异定义为如下

(14)

定义5 簇间离散度distexter， 表示各分组Ck内某连续属性Aj的均值μjk与整个数据对象上此属性的均值μj的离散程度。从样本集X随机抽取样本xi， 利用式(13)在每个与xi不同类的簇内寻找xi的非同类K近邻样本，记为Near_exterj,j=1,2,…,k。 样本xi与Near_exterj在特征Al上的差异定义如下

(15)

其中，C≠class(xi)。 样本集X在特征Al上的权重更新公式如下

(16)

由式(16)可知，数值属性的权值的主要由distinter和distexter的差值决定。distinter越小，distexter越大，样本与Near_interj在该属性上的相似度越高，样本与其Near_exterj在该属性上的相似度越低，该属性对于聚类的区分度越好，其权重也就越大。

2.3 分类属性的权值计算

分类属性的概率分布通过数值统计即可得知，本文采用信息论中的MI来计算分类属性权值。MI用来度量两个随机变量之间的相关性，表示在已知其中某个随机变量的条件下，另一个随机变量不确定性减少的程度。本文应用MI来衡量样本分类属性与聚类结果之间的依赖程度，从而求出样本分类属性对聚类的重要程度。

Dom(Al)={al|al=xil,1≤i≤n,p≤l≤m} 表示样本集X第l个属性的所有值组成的集合， |Dom(Al)| 表示分类属性Al的取值个数。Av=Dom(Al=v) 表示xil=v的样本子集，随机变量R={Ci|i=1,2,…,k} 表示样本的聚类结果，定义p(a),p(r),p(a,r) 分别表示Al和R的边缘概率分布函数以及Al，R的联合概率分布函数，其中

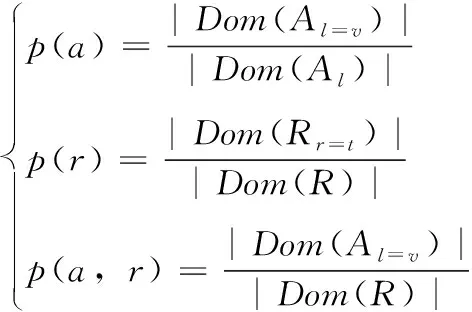
(17)

则分类属性Al与聚类结果R之间的互信息MI定义如下

(18)

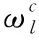
(19)

根据式(12)、式(15)和式(19)，WFKP算法对目标函数进行了相应的修正，修正后的目标函数如下

(20)

2.4 簇中心更新

对式(20)求最小值以获得最优解，需要遍历样本集所有可能的簇划分，理论上属于NP-Hard问题。本文采用贪心策略，通过对簇中心迭代更新寻找其近似最优解，文献[11]证明了经有限次迭代后目标函数可以收敛于局部最优解。本文在对簇中心进行迭代更新时，增加对属性权重的计算，快速筛除冗余属性，有效减少迭代次数，提高聚类效率。对簇中心cj的第l(1≤l≤p) 个数值属性cjl的更新公式如下

(21)

对于簇中心ci的第l(p+1≤l≤m) 个分类属性cil的更新公式如下

(22)

其中，s满足如下定义

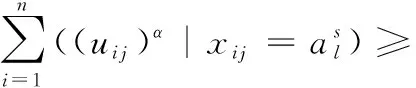
(23)

综上，WFKP聚类算法描述如下。

步骤1 指定聚类类别K[12]，初始化簇中心[13]。

步骤2 初始化迭代次数t=0， 初始化簇中心矩阵C(t)， 初始化目标函数值E(t)=0。

步骤3 利用式(4)计算迭代模糊划分矩阵U(t)。

步骤4 利用式(15)计算数值属性的权值矩阵Wn(t)， 利用式(19)分类属性的权值矩阵Wc(t)。

步骤5 利用式(21)、式(22)更新簇中心。

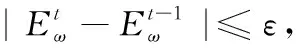
3 实验结果与分析

在UCI数据集和培养质量数据集上验证WFKP算法的有效性和实用性，选取KP算法、FKP算法、IG-F-KP算法、GK-KP作为对比算法。算法使用C#语言实现，运行在Window10操作系统上，实验的硬件配置为：Intel(R) Core(TM) i7-8700K CPU @3.70 GHz，内存为8.0 GB。

3.1 UCI标准数据集验证

本文使用的数据集为Iris Plants(简称Iris)、Credit Approval(简称Credit)、Heart Disease(简称Heart)以及Wisconsin Breast Cancer(简称Breast)，数据集的相关描述见表1。

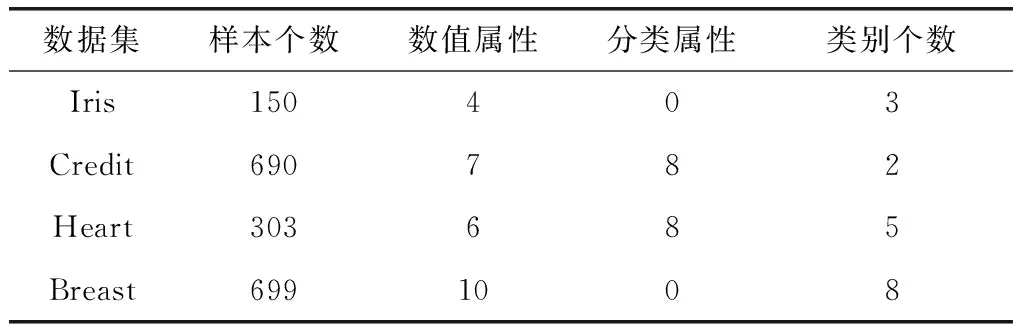
表1 UCI数据集描述

实验采用准确率(Accuracy)来验证WFKP算法的有效性和鲁棒性[14]。假设样本集中样本数为n，Ai表示样本正确分到第i类的样本数，k为聚类数目，则准确率的计算公式如下

(24)

聚类分析中参数的设置至关重要，对UCI数据的验证中，参数k由UCI数据集指定，模糊因子α设置为2[15]，停止阈值设置为0.0001，λ取分类属性与连续属性的比值。不同算法在Credit数据集的准确率如图1所示。

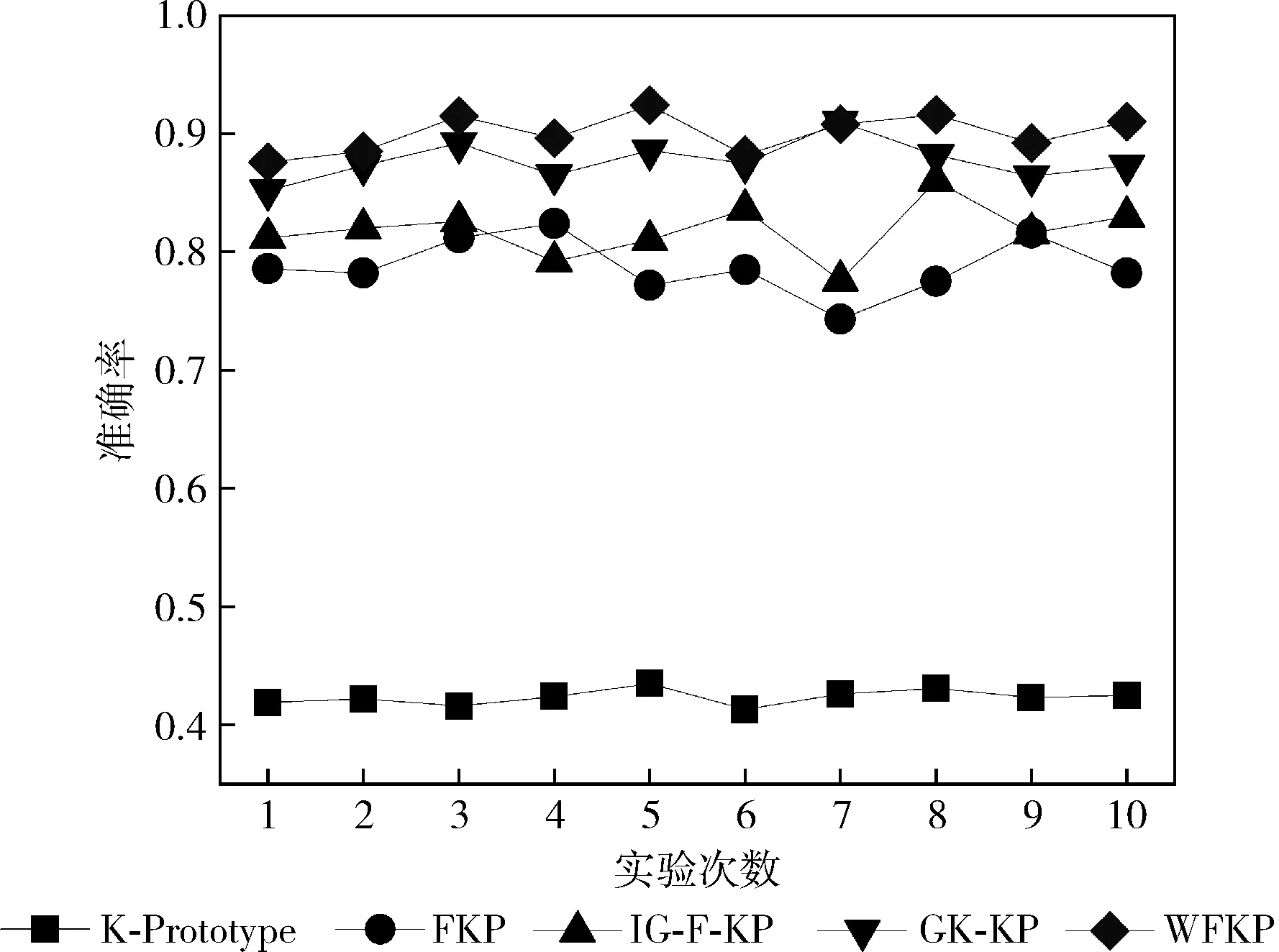
图1 不同算法在Credit数据集的准确率

从图1可以看出，KP算法在Credit数据集上准确率最低，在其基础上改进而来的各种聚类算法准确率得到了显著的提升。其中，WFKP算法在Credit上的准确率明显高于传统的K-Prototype的算法，与其它聚类算法相比准确率也处于较高水平。

不同算法在表1所示数据集上进行对比实验，各算法的平均准确率见表2。

表2 不同算法的平均准确率

从表2可以看出，在相同数据集上，WFKP算法在Iris上的准确率最高，比GK-KP算法平均提升1.4%，比IG-F-KP算法平均提升3.2%；WFKP算法在Heart上的准确率最低，略低于GK-KP算法0.7%，高于IG-F-KP算法0.4%。WFKP算法的在UCI数据集上的整体准确率要高于其它对比算法，验证了算法的有效性。

为了进一步检验WFKP算法在表1所示数据集上的聚类性能，本文结合PCA算法和t-SNE高维数据可视化算法[16]，保留原有数据结构的基础上对表1中的数据集进行降维分析，直观展示聚类效果。WFKP算法的聚类可视化结果如图2～图5所示。

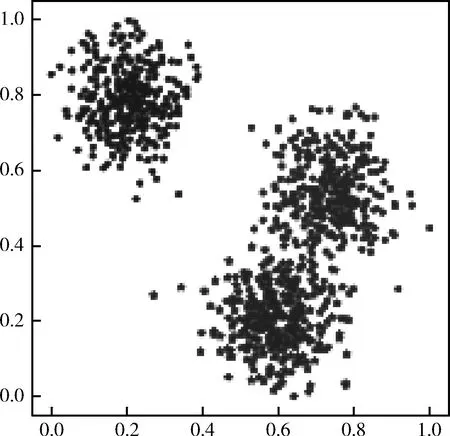
图2 Iris数据集：聚类可视化效果

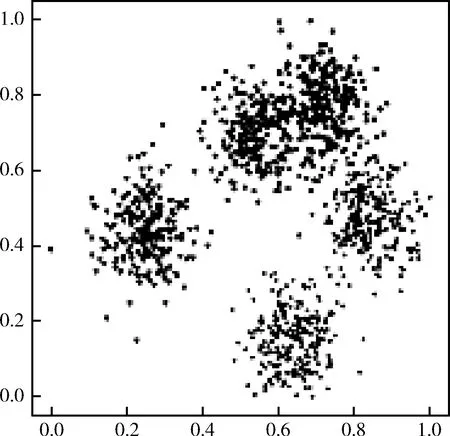
图4 Heart数据集：聚类可视化效果

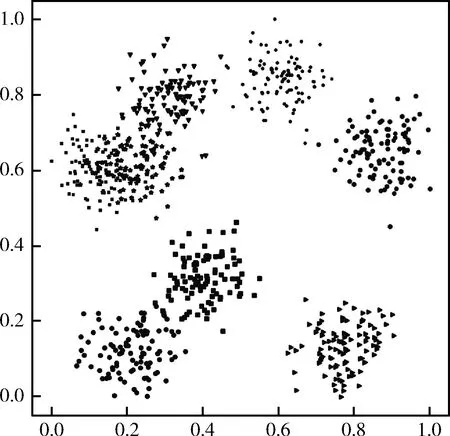
图5 Breast数据集：聚类可视化效果

观察图2～图5可以发现，WFKP聚类算法在4种UCI数据集上均具有良好的可分性。其中，Iris数据集只有4个特征维度的数值属性，其数据集相对简单，数据重叠部分最小，聚类分布效果最为良好。Heart具有7个维度的数值属性和8个维度的分类属性，这基本与研究生培养质量评估数据集的特征维度相符合。WFKP在Heart数据集上的重叠部分多于Iris，聚类效果略差于Iris，但也有较好的聚类可分性，这验证了WFKP聚类算法的有效性和鲁棒性。

3.2 培养质量数据集验证

培养质量评估首先需要确立评估指标体系，评估指标体系是基于培养质量评估的内涵构造的具体的可量化的评价准则。文献[17]结合德尔菲法和层次分析法构建出多角度深层次的培养质量评价指标体系，避免过多的评价特征造成维数灾难。在文献[17]的基础上，结合高校研究生培养的实际需求，构建如表3所示培养质量评估指标体系。

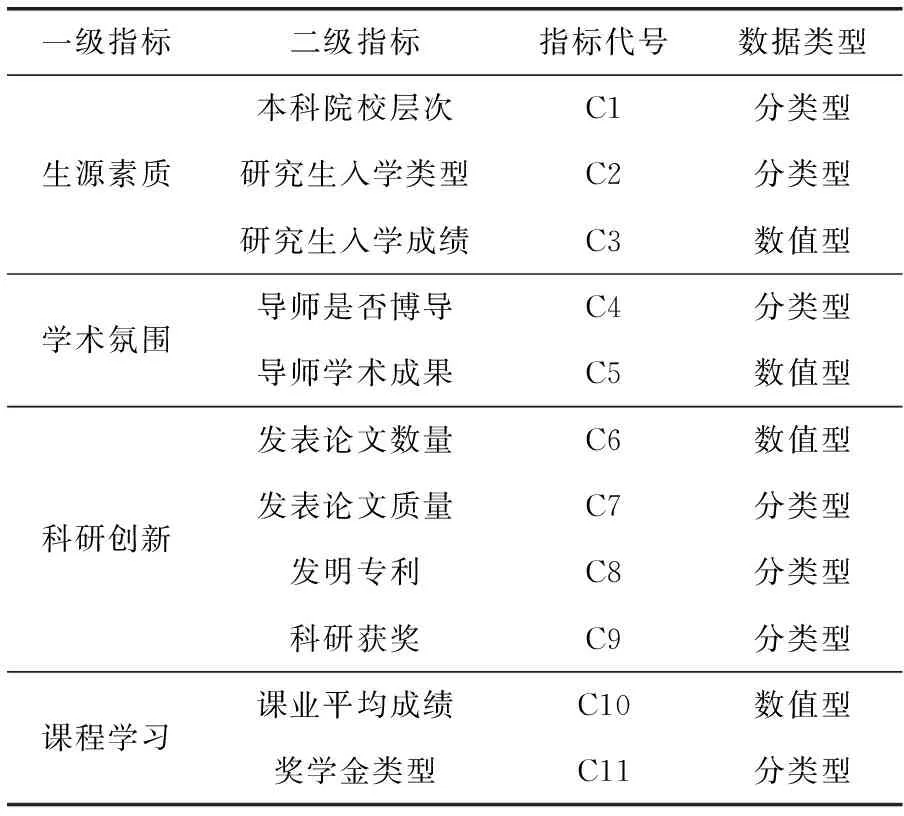
表3 研究生培养质量评估指标体系

参照表3构建的评估指标体系，采集某高校2015级至2018级14 268名研究生培养信息，将其映射为11维的特征向量，获得14 268×11维的培养质量数据集。数据集中的部分样本数据见表4。

由于培养质量数据之间具有量纲差异性，不便于比较，本文采用极差正视化方法将每个样本的数值属性缩放到0～1

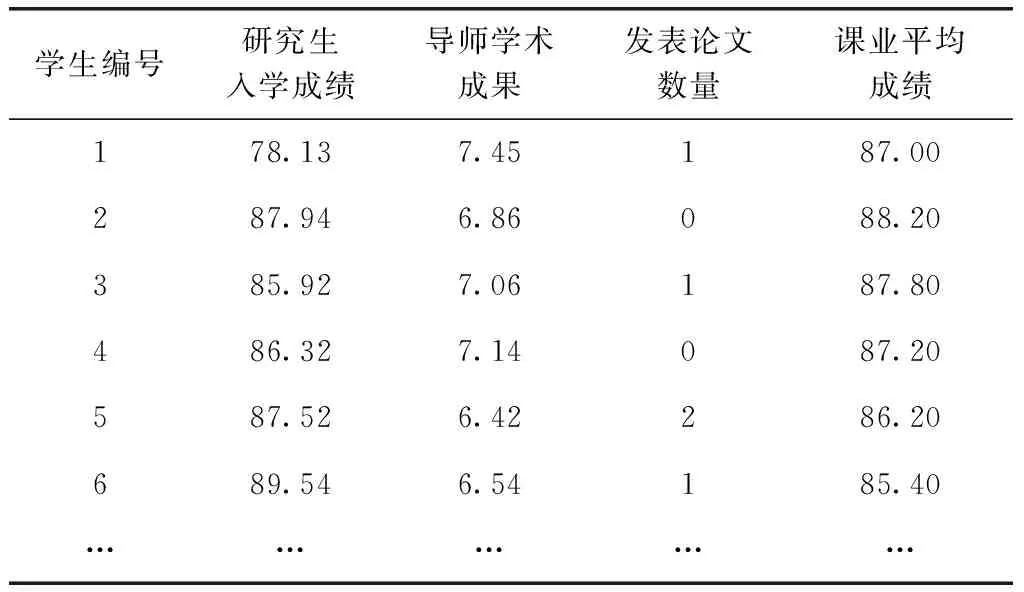
表4 研究生培养质量样本数据(数值属性)

的范围，转化为无量纲数值，便于不同单位或量级的指标进行比较和加权[18]，极差正式化方法如式(25)所示。对培养质量数据数值属性进行极差正视化处理处后的样本数据见表5

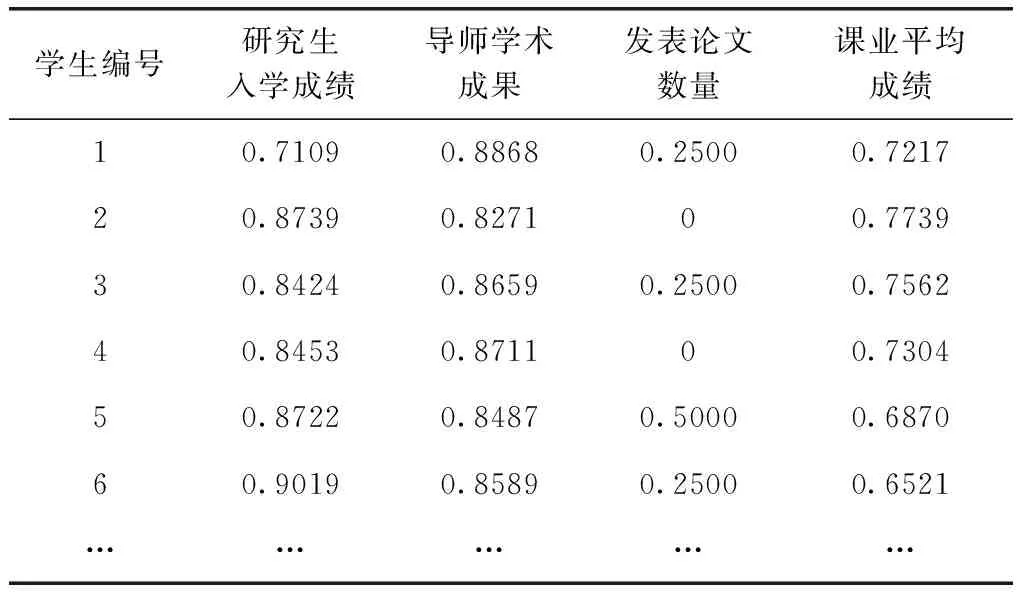
(25)

WFKP是无监督算法，培养质量这种无标签的数据，在没有先验知识的前提下无法直接通过准确率来验证聚类算法的有效性，我们使用轮廓系数SC(silhouette coef-ficient)来验证WFKP在培养质量数据集的聚类性能。

SC的计算公式如下

(26)

式中：ai体现聚类的凝聚度，表示样本i到簇Ci内其它样本的平均距离，bi体现聚类的分离度，表示样本i与簇Cl(l≠i)内样本的平均距离。SC结合了聚类的凝聚度和分离度，区间取值为[-1,1]。SC值越接近于1，表示聚类的凝聚度越大，分离度越小，聚类效果越好。

对培养质量数据进行聚类分析时，参数k设为4，λ的值设置为1.1，模糊因子的取值对培养质量的聚类分析影响较大，设置多组实验对模糊因子不同值进行聚类分析，实验结果见表6。

从表6可以看出，当模糊因子值为1.5时，算法的平均

表6 培养质量聚类评估的轮廓系数

轮廓系数值为0.851，算法在培养质量数据集上达到最佳的聚类效果。

设定模糊因子α的值为1.5，利用WFKP算法对培养质量数据进行聚类分析，当目标函数收敛后，获得研究生培养质量评估要素的权重分析，如图6所示。研究生培养质量的聚类统计结果如图7所示。

图6 培养质量属性权重分析

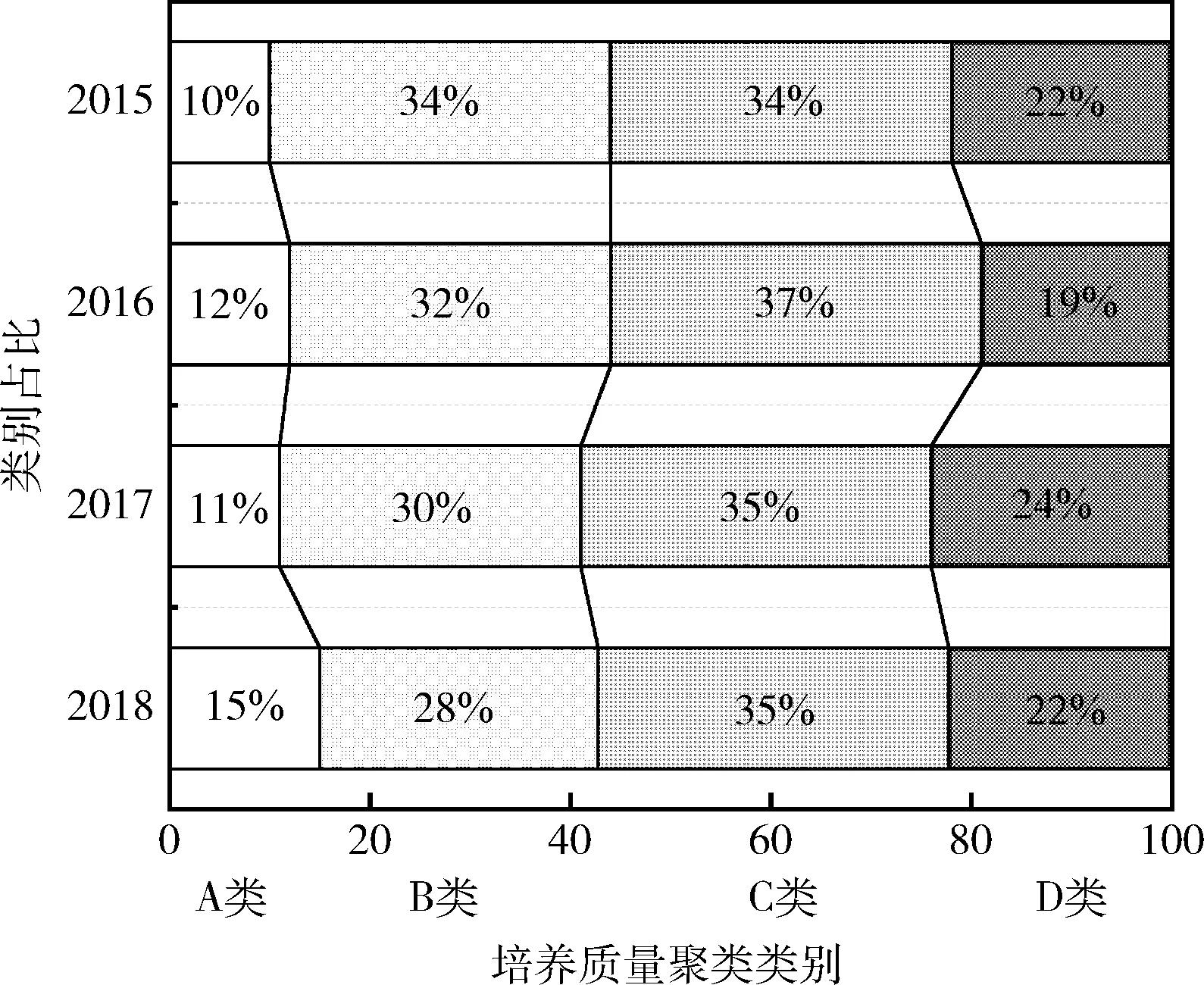
图7 培养质量聚类类别统计

通过对培养质量的权重分析(图6)和WFKP加权聚类的各类别占比统计分析(图7)，得出以下结论。

(1)研究生培养质量评估要素中，权重最高的是导师学术成果和学生论文质量，4年的平均权重值分别是17.4%和13.5%；权重最低的是本科院校层次和研究生入学成绩，权重占比分别是4.3%和2.6%。学术氛围和科研创新的权重逐年上升，生源素质的权重略有下降。导师学术成果的权重由2015级的14.4%上升至2018级的19.1%，学生入学成绩的权重由2015级的2.8%下降至2018级的2.5%。这说明，导师的学术水平和培养过程精细化要求起着至关重要的作用，而本科院校层次和研究生入学类型对培养阶段影响较小，研究生的培养质量重在培养，研究生入学后应在导师的指导下把更多精力投入到学术研究中，提高自身科研能力。

(2)研究生培养质量聚类类别中，平均占比最大的是B类和C类，分别占比31%和35.2%；平均占比最小的是A类和D类，分别占比12%和21.7%，研究生培养质量整体呈现两头小中间大的分布。学校逐年加强导师学术能力的考核和学生科研能力的培养，研究生教育改革取得一定的进步，A类研究生占比由10%上升至15%，B类研究生占比由34%下降到28%。C类和D类研究生占比基本稳定在57%，研究生培养质量还有较大的提升空间。

4 结束语

传统模糊聚类算法未能考虑样本间的总体差异，忽略样本的特征关联和特征权值，降低了算法结果的稳定性和准确性。针对此问题，在马氏距离的协方差矩阵估计中引入比例系数来计算分类属性相异度，利用新的相异度来寻找样本点的K个近邻点，用于计算样本的簇内和簇间相异度分析数值特征的权值，通过计算分类特征和聚类结果之间的互信息分析分类特征的权值。在UCI真实数据集上验证了WFKP算法的有效性和鲁棒性，并将本文算法应用到研究生培养质量评估中。通过对培养质量数据集进行聚类分析，刻画研究生培养质量的分布比例，重点分析不同评估要素对培养质量的影响权值，为高校提升培养质量提供相应的决策支持。