基于时序隐变量模型的因果关系发现算法

曾 艳，郝志峰,2+，蔡瑞初，谢 峰

(1.广东工业大学 计算机学院，广东 广州 510006；2.佛山科学技术学院 数学与大数据学院， 广东 佛山 528000；3.北京大学 数学科学学院，北京 100080)

0 引 言

传统的因果关系发现算法多数专注于探索可观测变量之间的因果关系[1-6]，然而，在现实生活中，事物本质的因果关系并不是位于可观测变量中，而是位于隐变量(latent variables)中，例如焦虑、失望或处理事物的能力等[2,7]。因此，从观察数据中发现隐变量间的因果关系近年来获得了不少研究学者的兴趣[7-9]。

经典的从观测变量中发现隐变量的因果关系算法可以分为两类：基于高斯性和基于非高斯性的算法。基于高斯性的算法[7,10]主要利用了数据结构中的协方差信息，进而确定隐变量之间的马尔科夫等价类结构。基于非高斯的算法[9,11]等使用了数据的非高斯性，解决了该不可唯一识别的问题。这些工作专注于研究静态贝叶斯网络的模型。然而，在实际应用领域中，特别是在经济学中，因果效应往往在动态贝叶斯网络中体现，而不仅仅发生在瞬时的因果关系中。如果此时忽略考虑瞬时效应或者延时效应，那么在因果结构的估计中将会引入额外的错误而导致不合理的解释。现有的基于结构向量自回归模型(structural vector autoregression model，SVAR)[12]的工作考虑了可观测变量的瞬时性和延时性的因果效应，但没有考虑隐变量的情况。

因此，本文首先构建了时序隐变量模型(latent factor models for time-series data，LFTS)，考虑了隐变量之间的瞬时性和延时性的因果效应，提出了基于LFTS模型的因果关系发现算法。该算法采用了三阶段的方式估计模型的网络结构，包括隐变量之间的瞬时因果效应矩阵与延时因果效应矩阵。最后，通过仿真数据实验，表明了算法的有效性。

1 相关工作

1.1 结构向量自回归模型

自回归模型(autoregressive model，AR)[12]是统计上一种处理时间序列数据的方法，被广泛运用在经济学、资讯学、自然现象等领域上。结构向量自回归模型(structural vector autoregression model，SVAR)是AR模型由一个变量到多个变量的扩展，同时它不仅考虑了各个变量之间的延时效应，而且考虑了即时性的结构关系。值得注意的是，传统的AR模型和贝叶斯网络(Bayesian networks，BN)或结构方程模型(structural equation models，SEM)均属于SVAR模型的特殊形式，SVAR模型是AR模型与SEM模型的结合体。SVAR模型旨在学习随机变量之间的延时效应矩阵与瞬时效应矩阵，从而达到预测的目的或者实现因果关系的分析，提高对数据的可解释性。

其数学表示为：假定在一个平稳时间序列上有M个独立的样本，xm,t表示第t个时间序列的第m个数据样本，则其p阶SVAR模型可以如式(1)所示

xm,t=B0xm,t+B1xm,t-1+…+Bpxm,t-p+em,t

(1)

其中，t∈{p,…,T}，m∈{1,…,M}，em,t表示对应的噪声变量且它们之间在不同时间序列和在同一个时间序列上互相独立。Bi,i∈{1,…,p} 表示延时效应矩阵，而B0表示瞬时效应矩阵，它们属于SVAR模型的回归参数。

1.2 隐变量模型

隐变量模型[7]，也称为隐因子模型(latent variable/factor models，LVM/LFM)，是统计学上用以描述可观测变量和不可观测变量(隐变量/隐因子)之间关系的经典模型。该模型被广泛应用于心理学、社会学和教育研究等领域中。隐变量模型通常假设可观测变量由隐因子产生。特别地，当所有变量都是连续的随机变量时，从SEM的角度上看，隐变量模型可以表示为如下的数学表达式

fm=Bfm+em

(2)

xm=Gfm+nm

(3)

其中，fm,xm分别为隐变量向量与可观测变量向量的第m个样本；em,nm分别为fm与xm的噪音变量向量的第m个样本。B是表示连接强度矩阵而G是因子载荷矩阵。B表示隐变量之间的因果结构关系，而G表示可观测变量与隐变量之间的联系。通常地，式(2)被称为该隐变量模型中的结构模型，而式(3)被称为测量模型。

由于隐变量的不可观测性，该模型的估计一直以来被认为是一个难点和挑战。早前的估计工作主要利用了数据的高斯性，然而这类方法会产生许多不可识别的结构模型[7,10]；为了克服不可识别性的问题，近年来，学者们专注于利用数据的非高斯性，实现模型的唯一识别性[8,9]。然而，上述方法主要估计的是静态的隐变量模型，而具有时序信息的动态数据在现实生活中却是常见的。因此，研究时序隐变量模型的因果关系发现算法是必要且重要的。

2 基于时序隐因子模型的因果关系发现算法

本节在相关工作的基础上建立了面向时序数据的隐因子模型，接着提出了基于该模型的因果关系发现算法。

2.1 时序隐变量模型

本文将隐变量模型扩展到时间序列上，提出了时序隐变量模型，简称为LFTS，其数学表达式具体如下

fm,t=B0fm,t+B1fm,t-1+…+Bpfm,t-p+em,t

(4)

xm,t=Gfm,t+nm,t

(5)

其中，fm,t,xm,t表示第t个时间序列隐变量、可观测变量的第m个数据样本，t∈{p,…,T}，m∈{1,…,M}， 自回归阶数为p阶，Bi,i∈{1,…,p} 表示隐变量的延时效应矩阵，而B0表示隐变量之间的瞬时效应矩阵。值得注意的是，在t时刻，隐变量之间的因果关系网络是一个有向无环图，所以在经过一系列的矩阵变换操作之后，瞬时效应矩阵B0可以变换成为一个严格的下三角矩阵。em,t,nm,t分别为隐变量、可观测变量的噪音变量向量在第t个时间序列的第m个样本，G是因子载荷矩阵。类似地，本文称式(4)为LFTS的结构模型，而式(5)为其测量模型。

为了获得模型的识别性[9,13]，假设噪音向量em,t,nm,t在时刻t内或者在时间之间是互相独立的；噪音变量服从非高斯分布；每一个隐变量至少产生两个纯测量变量(纯测量变量指的是只由一个隐变量父亲产生的可观测变量[2])。式(4)可以重写为如下向量自回归模型的形式

(I-B0)fm,t=B1fm,t-1+…+I-Bpfm,t-p+em,t

(6)

fm,t=A1fm,t-1+…+Apfm,t-p+εm,t

(7)

其中

Ai=(I-B0)-1Bi

(8)

εm,t=(I-B0)-1em,t

(9)

I为单位矩阵。由此可知，式(7)是向量自回归模型的简化型。除此之外，由式(9)可得

εm,t=B0εm,t+em,t

(10)

其中

εm,t=fm,t-A1fm,t-1-…-Apfm,t-p

(11)

由式(10)以及本文所做的假设可知，LFTS模型中的隐变量的残差εm,t在本质上服从线性非高斯无环模型(linear non-Gaussian acyclic models，LiNGAM)[14]。而式(5)的测量模型直接是隐因子模型的简化型。

图1提供了本模型的一个例子，即，一个具有3个隐变量、每个隐变量下具有2个纯测量变量、自回归阶数为2的时序隐变量模型。如图1所示，不同的底色显示不同的时间序列，即时间为(t),(t-1) 和 (t-2) 以及p=2。 方形的节点表示隐变量，圆形的节点表示可观测变量。fi或xi表示第i个隐变量或可观测变量。隐变量之间的实线箭头表示瞬时效应矩阵B0， 而虚线箭头表示延时效应矩阵Bi。 隐变量与可观测变量之间的关系使用实线箭头的G表示。由图1可知，以第m个样本为例， (t)时刻下的f1受到 (t-1) 时刻下的f1和f3， 以及(t-2) 时刻下的f1共同影响； (t) 时刻下的f2受到同时刻的f1、 (t-1) 时刻下的f2以及 (t-2) 时刻下的f2共同影响。所以，可以定义问题如下：

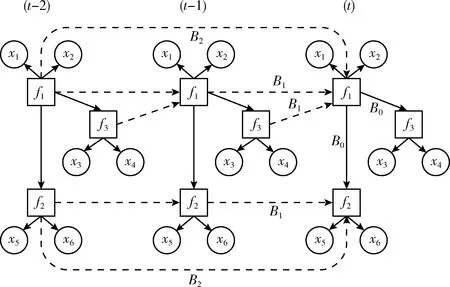
图1 本文时序隐变量模型

2.2 LFTS算法

(12)

式(12)由式(5)推导而成，且在噪声变量足够小时或者测量变量的个数足够多时成立。

由上一小节分析可知，式(4)表示的是结构向量自回归模型，它不仅刻画了隐变量之间的瞬时效应矩阵B0， 而且描述了不同时序下隐变量之间的延时效应矩阵Bi。 式(4)可以转换成式(7)。由式(7)可知，隐变量fm,t可以表示为过去p个时间序列隐变量的线性组合形式和噪声εm,t之和，也就是，在本质上式(7)属于经典的向量自回归模型的简化型，其中矩阵Ai是自回归矩阵，p是隐变量延时的时序个数，即自回归阶数，而噪声εm,t是革新过程。值得注意的是，当瞬时延时矩阵B0为零矩阵时，式(4)的模型则不需要经过变换，其自身已经是一个向量自回归模型。

εm,t=Wem,t

(13)

其中

W=(I-B)-1

(14)

(15)

2.2.4 算法伪代码

根据前文对算法流程的描述，现将LFTS算法的伪代码列出如算法1所示：

算法1：LFTS算法

输入：具有时序信息的数据集X， 自回归阶数p。

(1)归一化处理数据集X；

3 实验结果与分析

为了验证和分析本文提出算法的有效性，本文在模拟数据集上做了验证实验与对比实验。具体来说，本文从两个方面验证算法的有效性：3.1考虑隐变量之间因果延时效应的验证实验，使用热力图描述估计的瞬时效应矩阵B0、 延时效应矩阵Bi， 体现本算法的有效性；3.2不考虑隐变量之间因果延时效应的对比实验，此时，选取经典的LiNGAM[14]与Notears[5]方法作为隐变量之间瞬时因果结构的估计方法，这两类方法没有考虑隐变量之间的因果延时效应。

模拟数据的生成主要通过两个阶段来实现：首先，令自回归系数为1，先随机产生瞬时效应矩阵B0、 延时效应矩阵Bi和隐变量的因果次序(因果关系的强度在[-0.7,-0.2]∪[0.2,0.7]之间取得)。给定样本量，噪声变量em,t的分布为非高斯分布，根据式(4)随机产生LFTS模型中的结构模型的隐变量模拟数据fm,t。 紧接着，假定每个隐变量下具有2个纯的测量变量，随机产生[-0.7,-0.2]∪[0.2,0.7]之间的因子载荷矩阵G， 噪声变量nm,t的分布为高斯分布，再根据式(5)随机产生LFTS模型中的测量模型的可观测变量数据xm,t。

3.1 考虑延时效应的实验分析

本小节主要进行了不同样本量情况下的模拟数据实验：设置隐变量的个数为5，可观测变量个数为10，样本量为100,200,500,1000。由于本算法旨在发现时序隐变量模型的网络因果结构关系及其相应的因果强度，本文将真实的B0,Bi和估计的B0,Bi作为输出结果作对比，即使用热力图描述实验输出的瞬时效应矩阵B0和延时效应矩阵Bi。 图2～图5展示了算法在不同样本量下的真实矩阵B0,Bi与估计矩阵B0,Bi的对比图，其中，图(a)～图(d)分别为真实的B0、 估计的B0、 真实的B1和估计的B1的热力图。当真实的因果效应矩阵图(a)、图(c)与估计的效应矩阵图(b)、图(d)越相似，则实验效果越好。当样本量为100,200和500时，实验设置了不同的随机种子，所以每次实验产生的真实结构都会发生变化。由图2至图4所示，总体来看，算法估计的网络结构图(b)和图(d)的因果强度与真实的因果强度图(a)和图(c)是令人满意的，不管是对于瞬时的隐变量之间的结构B0来说，还是对于延时的不同时序隐变量之间的结构Bi来说。具体地说，当因果网络结构趋于稠密时，如图2～图4中的B1， 算法可能会估计少或多1-2条边，这可能是因为剪枝算法中的剪枝强度过大或过小。在现实生活中，可以根据实际情况或数据的背景知识，选择合适的剪枝算法避免估计出缺失或者多余的因果结构。

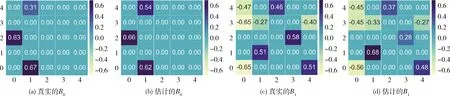
图2 样本量为100的真实矩阵B0,Bi和估计矩阵B0,Bi对比结果

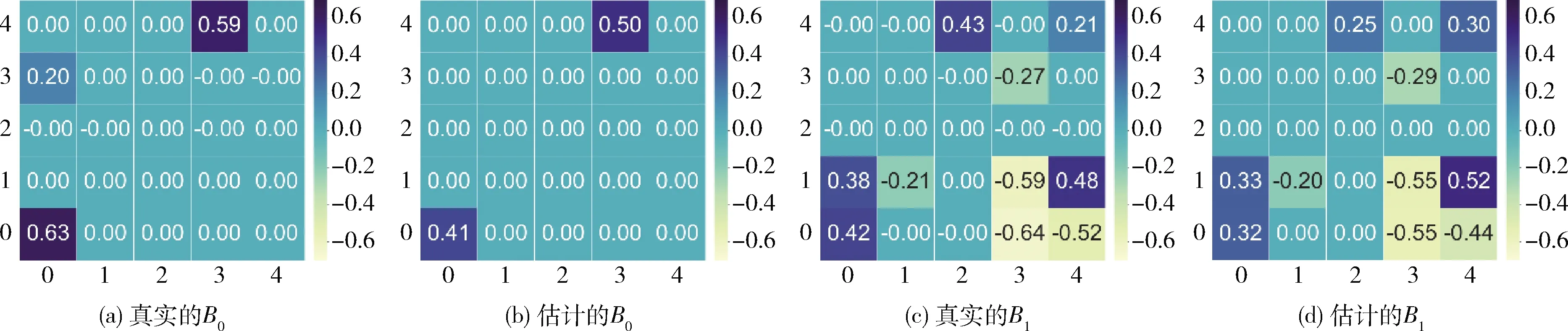
图3 样本量为200的真实矩阵B0,Bi和估计矩阵B0,Bi对比结果

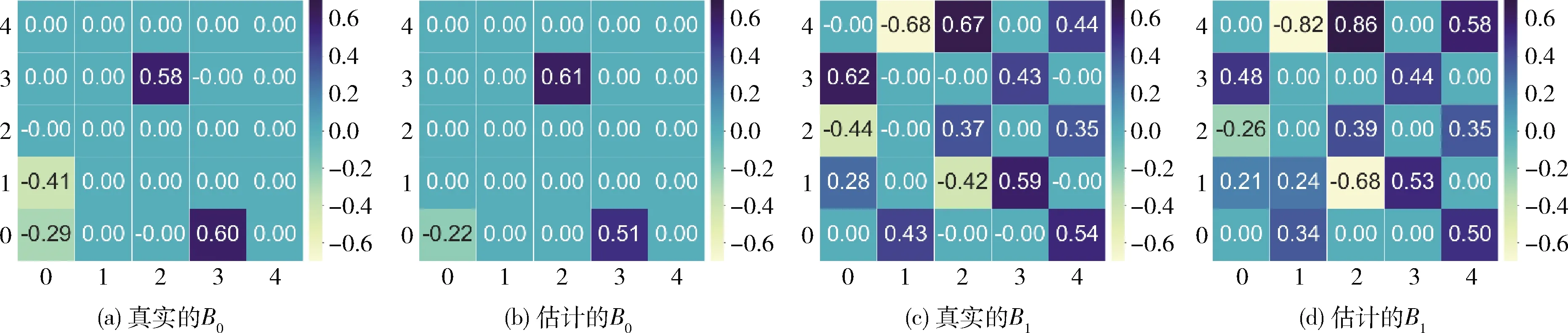
图4 样本量为500的真实矩阵B0,Bi和估计矩阵B0,Bi对比结果

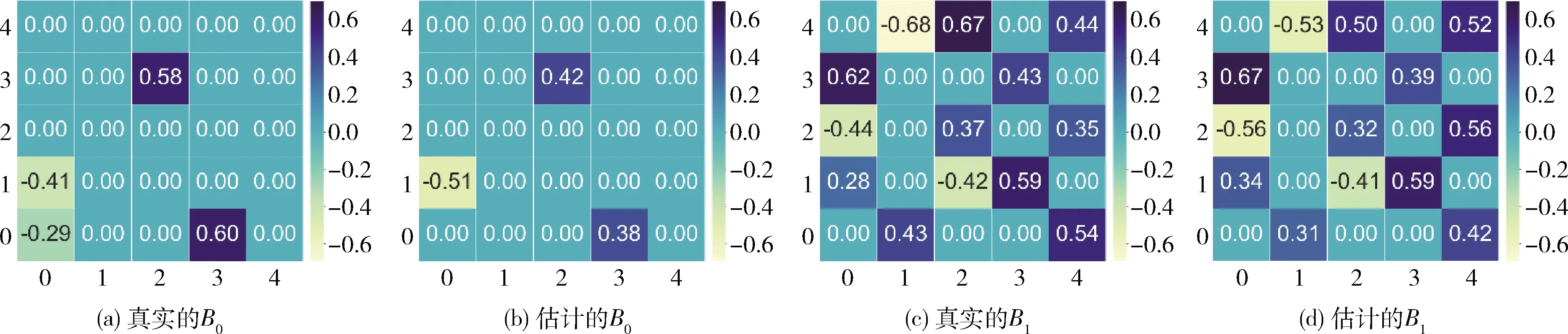
图5 样本量为1000的真实矩阵B0,Bi和估计矩阵B0,Bi对比结果

此外，当样本量为1000时，设置了和样本量为500的实验一样的随机种子，可以发现，当固定随机种子时，随着样本量的增大，实验的效果有一定的提升。特别是对于延时效应矩阵Bi来说，其学习到的因果结构更加准确，且因果强度更贴近于真实值。所以，总体来说，算法在时序隐变量模型的因果关系发现问题上具有较好的实验效果。

3.2 不考虑延时效应的实验分析

为了说明考虑因果延时效应的必要性以及本算法在考虑因果延时效应方面的有效性，本小节选取了经典的LiNGAM[14]与Notears[5]方法作为隐变量之间瞬时因果结构的估计方法，这两类方法均没有考虑隐变量之间的因果延时效应。本文采用召回率(Recalls)、准确率(Precisions)和F1得分(F1)作为因果瞬时效应矩阵的评估指标。F1得分反映了隐变量因果网络结构的总体估计优劣，具体为

(16)

其中，TP表示正确估计的边的个数；FP表示未估计到的边的个数；FN表示错误估计的边的个数。本小节设置了在不同样本量100,200,500,1000下，不同隐变量个数3,4,5,6的实验效果。结果取50次独立随机实验的平均值。结果如图6～图9所示。

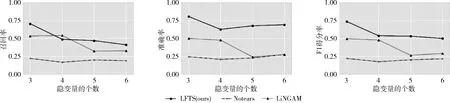
图6 算法在样本量为100时的实验效果

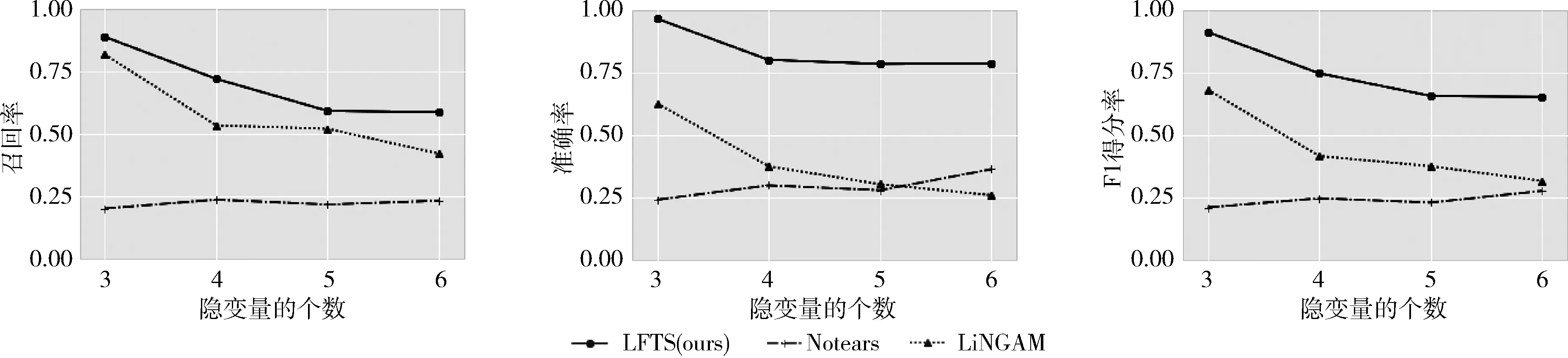
图8 算法在样本量为500时的实验效果

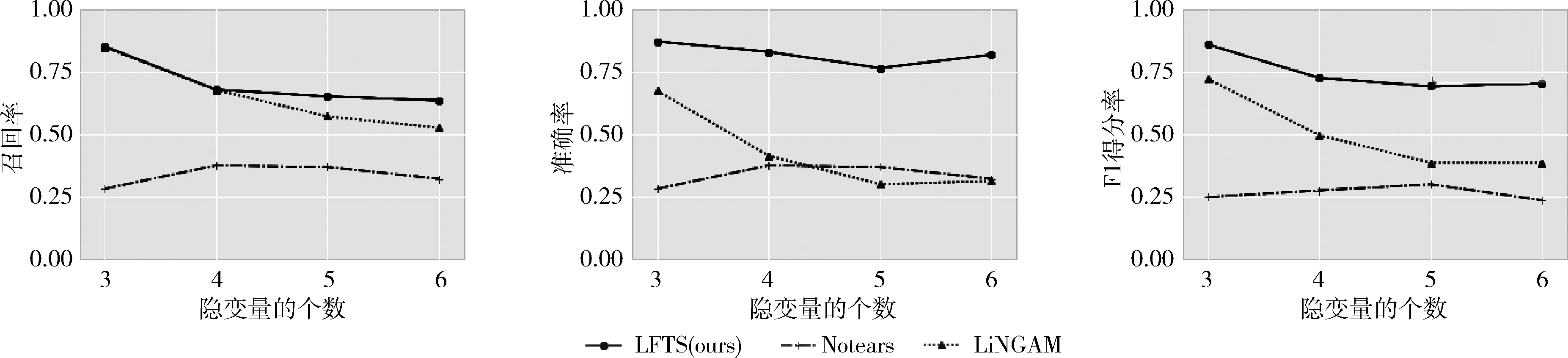
图9 算法在样本量为1000时的实验效果

从图6～图9的结果图分析发现，随着样本量的逐渐增加，所有算法的3个指标都呈现不同程度上升的趋势，且本文提出的LFTS算法均优于其余两个对比算法，说明本算法的有效性。具体地来说，当样本量小于500时，LFTS算法随着样本量的增加而效果提高显著，当样本量为500或1000时，其效果提升的幅度相对稳定，这意味着算法在样本量大于500时对样本量的鲁棒性提高。此外，LFTS算法几乎在每个不同设置下的实验都优于其余算法，充分地说明了考虑延时因果效应的重要性。如果忽略了该效应，那么在估计瞬时因果效应矩阵时，会大大地降低估计的准确性，影响了最终隐变量因果网络结构，包括方向的估计，从而影响了实验数据最终的解释性。

4 结束语

从观测变量中发现隐变量之间因果关系的算法近年来获得越来越多学者的关注。本文在现有隐变量模型的基础上，考虑了隐变量之间的瞬时因果效应与延时因果效应，创建了时序隐变量模型(latent factor models for time-series data，LFTS)，并提出了一种三阶段的因果关系发现算法，估计了LFTS模型的因果网络结构，包括瞬时因果效应矩阵与延时因果效应矩阵。实验结果表明，本文提出的LFTS算法具有较好的学习效果，具有较高的估计瞬时因果效应与延时因果效应的准确率。如何使用统一的框架实现同时估计瞬时因果效应矩阵与延时因果效应矩阵，是下一个阶段的工作重点。