基于函数的数控宏程序编制与应用*

徐晓翔，储晓猛

(江苏大学机电总厂，江苏 镇江 212013)

0 引 言

近年来各种基于CAF/CAM软件的数控编程已经成为潮流，但是手工编程还是基础，各种“疑难杂症”或批量产品的解决往往还要利用手工编程。且手工编程还可以使用变量编程，即宏程序的运用，可将有规律的尺寸或形状用简短的程序段表示出来宏程序可以使用变量，并给变量赋值，变量之间可以运算，程序运行可以跳转(普通程序不能实现此功能)，其具有极好的易读性、易修改性、逻辑严密和通用性强等优点。宏程序短小精悍，机床在执行此类程序时，完全容纳得下任何复杂的宏程序，无需考虑机床与外部电脑的传输速度对于实际加工速度的影响，即使是最廉价的机床数控系统，较执行CAD/CAM软件生成的程序更加快捷，反应更迅速[1-2]。

在数控车床实际生产加工中，经常遇到满足数学中一次函数关系的加工型面例如：锥度、外圆、梯形螺纹等。常规手工编程的方法是根据每种零件的尺寸及结构，编制出相应的程序，如果零件发生变化，只能重新编制。此方法虽能够解决零件的数控加工问题，但存在程序编制重复性的劳动多，工作量大，编程效率低等问题。为了提高编程效率、减少编程工作量，笔者针对外圆锥度零件的加工问题，通过采用宏程序的加工方案，将满足数学中一次函数的加工型面做成通用性的模板，在实际编程中调用该模板修改相对应的变量值即可，既能节省编程时间又能保证程序的准确性。

1 编程思路

从数学知识可知，函数是应变量随着自变量变化而变化的集合。函数的对应法则是应变量与自变量变化按照一定的规律变化，用数学关系表示F(X)=Y,其中()就是对应法则，X是自变量，Y是应变量，Y(应变量)随着X(自变量)变化而变化。

宏程序编程引用了变量，且变量与变量之间可以进行数学、逻辑运算；宏程序编程也可以准确表示一个变量随着另一个变量变化而变化的动态过程，所以宏程序编程本质与函数都是按照一定的规律变化。根据加工零件型面构建数学模型；根据数学模型、建立函数关系是宏程序编程基本步骤[3-4]。

一次函数型面零件，采用宏程序编程步骤：

(1)根据加工零件型面，构建数学模型。

(2)根据数学模型，找出相对应一次函数原型(线性变化规律)。

(3)根据一次函数原型，用代数关系式表示出自变量与应变量之间的关系(某一时刻)。

(4)将自变量与应变量之间的变化规律与加工零件结合起来。

(5)采用宏程序编程定义变量、变量之间进行运算、控制流向语句、逻辑关系……描述出一次函数(数学模型)变化规律。

(6)结合数控机床指令，编制加工零件宏程序代码。

2 实例分析

下面以图1所示零件为例，零件材料为45钢，需要加工其中的锥度部分(其中φ50 mm外圆已经加工)。

2.1 加工思路分析

从图1可知满足数学中一次函数关系式Y=KX+B(K≠0)线性关系表示式，建立数学模型如图2所示。采用宏程序编程时，优先考虑一次函数特性来进行分析，编程思路是根据零件轮廓的线性方程，计算出直径和长度的关系。具体过程如下：

(1)根据锥度轮廓的线性方程，由X(X作为自变量)计算对应的Z(Z作为应变量)或由Z(Z作为自变量)计算对应X(X作为应变量)，并计算下一次车削锥度X1、Z1的值。

(2)X轴(径向)快速移动至外圆直径尺寸(X1)，采用 G01方式车削Z轴长度值为Z1的外圆。

(3)上述构成了车削一次锥度粗加工的循环过程，在此基础上设置#100号变量控制加工余量10 mm，采用分层切削的方式，完成一次切削过程后，刀具退刀至切削加工起点，毛坯余量减小2 mm，再次进给2 mm，准备下一次切削，如此循环直到加工余量等于0时，跳出切削循环，至此零件加工完毕。

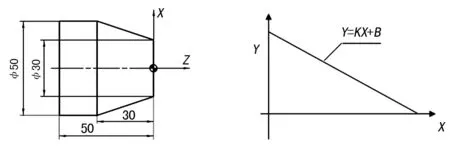
图1 加工零件示意图 图2数学模型示意图

2.2 数控程序编制

编制宏程序考虑其通用性，通常来说一种类型的宏程序对应一种类型的加工型面。当加工型面的一些要素如尺寸、大小、位置等发生改变，只要对相应的参数进行修改既可以满足加工要求。因此设置#101控制X轴尺寸变化、#102控制Z轴变化，通过锥度满足数学一次函数关系式：Y=KX+B(K≠0)，计算出#101(X轴)变化与#102(Z轴)的变化规律#103，加工程序如下：

O0001;(程序号)N1;(粗加工程序N1)T0101;(刀具调用)M03S2500;(机床主轴正转)G0X51Z1;(加工起点位置)M08;(冷却液开)#101=10;(设置#101号变量,控制锥度X轴变化)#102=30;(设置#102号变量,控制锥度Z轴变化)#104=50-30;(设置#104号变量,控制锥度大径与小径的差)#110=0.3;(设置#110号变量,控制精加工余量)#100=30;(设置#100号变量,控制锥度小段直径)#103=#104/[2∗30];(计算#103号变量的值,锥度的斜率)N10#101=#101-1;(#101号变量依次减去1mm)#102=#101/#103;(根据锥度线性方程,由X的值计算Z的值)#105=2∗#101+#100+#110;(计算#105号变量的值,程序中对应X的值)G0X[#105];(X轴移至X[#105])G01Z[0-#102]F0.2;(车削直线,去除毛坯余量)G0U1;(X轴沿正方向进给1mm)Z1;(Z轴移至Z1)IF[#101GT0]GOTO10;(条件判断语句,若#101号变量的值大于0,则跳转到标号为10的程序段处执行,否则执行下一程序段)G0X100;(X轴快速移至X100)Z100;(Z轴快速移至Z100)G28U0W0;(X、Z轴返回参考点)M05;(主轴停止)M09;(关闭切削液)M01;(选择性暂停,可用来中途检测加工尺寸)N2;(精加工程序N2)…(精加工程序省略)M30;(程序结束)

上述程序中，所设置的#101号变量，控制零件形状的X轴变化；#102号变量控制零件形状的Z轴变化。由X值(#101)根据一次函数方程Y=KX+B计算出X对应的Z值(#102)，然后X移动至X#101，Z轴车削外圆(粗加工)。

3 仿真验证

斯沃数控仿真模拟软件具有目前各种主流的数控系统和操作面板，软件具有手动编程和导入程序模拟加工两种模式。通过在PC机上操作该软件，将零件所对应的数控程序输入后，可进行模拟仿真加工，能够直观地看到虚拟加工的刀具路径和加工效果，从而达到验证编程效果的目的[5-6]。该数控仿真模拟软件工作界面如图3所示，将上述零件的宏程序输入至该数控仿真模拟软件，完成对刀等设置后，模拟加工出的零件如图4所示，通过该软件的检测功能，对加工后的零件进行检测，结果显示加工尺寸达到图纸要求，证实编程无误。

图3 斯沃数控车床仿真模拟软件工作界面 图4 仿真模拟加工零件

4 结 论

通过对上述实例中涉及的锥度零件进行分析，抽取出一次线性关系函数模型，分析了数控宏程序与一次函数内部关系，完成数控程序编制和仿真加工，得到了以下几个可以参考和借鉴的数控编程思路及方案。

(1)数学模型与宏程序变成密不可分的数学模型的构建和“程序化”是宏程序编程依据。

(2)数学模型到编制宏程序的基本过程：采用宏程序编程，通常先构建数学模型，根据数学模型找出与之对应的函数关系表达式，根据函数关系表达式找出自变量与应变量之间的变化关系，结合宏程序特定的编程语言，编制出被数控系统所识别的程序代码。

(3)“线性拟合法”是宏程序编程最基本思想，宏程序编程“动”与“静”贯穿整个编程过程，“动中取静”是宏程序的编程基础，学习和掌握宏程序编程的思想和原理，是编程实践的理论前提。