无人机视觉技术在道路裂缝分类中的应用

袁依文，雷 斌

（武汉科技大学机械自动化学院，湖北 武汉 430081）

1 引言

近年来，全国多发道路安全事故，造成了重大的人员伤亡与经济损失。调查结果显示大多数的道路安全事故是由裂缝引起的，裂缝作为道路工程中最严重的病害［1］之一，需有效监测，及时修缮。混凝土道路裂缝分为四类：纵向裂缝，横向裂缝，斜向裂缝和网状裂缝。不同的裂缝类型关系到不同的坏裂发展方向，不同的坏裂发展方向对道路安全造成的影响也是不同的。有效判断类型能预判裂缝坏裂发展走向，就能有针对性地进行道路修缮工作。

目前道路裂缝分类检测主要依靠人工检测或大型的检测车，人工检测劳动强度高且误差率高，大型桥梁检测车成本高。所以这里提出采用四旋翼无人机结合机器视觉技术对道路裂缝进分类检测，采用了支持向量机［2］的学习分类算法，算法关键在于设计合适的裂缝特征。国内外学者对于裂缝特征展开了一些研究工作。文献［3］提出将裂缝分布密度特征作为分类依据，此特征不能很好的将斜向裂缝与网状裂缝进行区分。文献［4-5］提出了通过图像背景连通域数量设置阈值来分类网状裂缝和线性裂缝，后通过比较裂缝在X轴与Y轴投影长度来分类横向裂缝与纵向裂缝，此方法不能分类斜向裂缝，且阈值判别法适应性较差。文献［6］选取裂缝的倾角，长宽比和空洞对裂缝进行分类，此法需确定三个相关的阈值，算法适应性较差。文献［7］提出根据裂缝曲率对裂缝进行分类的方法，此算法需还原裂缝三维图，算法计算量大，不适用快速分类。文献［8］提出将裂缝长度，宽度和角度作为特征对裂缝进行分类，但不能分类网状裂缝。文献［9］提出用裂缝方向角，块度和孔洞等特征进行分类，但不能将斜向裂缝进行分类。

上述采用的特征均能在一定程度上将裂缝进行分类，但因裂缝的复杂多变性，每种方法都不具有普遍适应性。文中提出了裂缝投影的方向性特征，裂缝骨架端点特征N，以及裂缝骨架与横纵网格交点数目比的特征R这三类特征进行裂缝分类，可有效区分这四类裂缝，精度高，速度快，适应性强。并进行了特征的对比实验，通过对裂缝分类正确率的对比分析，裂缝区域面积特征Area不能较好的将裂缝分类。结果表明，提出的这三类特征能达到较好地分类裂缝的目的。

2 无人机视觉检测方案设计

2.1 实验平台

针对于目前道路裂缝分类检测成本高，人工劳动强度大等问题，采用了四旋翼无人机作为分类检测的平台，四旋翼无人机体积小，便捷，且成本低。可通过遥控装置控制其飞行和悬停，飞行范围广且稳定，搭载相关硬件装置可对道路裂缝进行检测。

将摄像头、树莓派等设备装载在四旋翼飞行器上。摄像头接入树莓派，树莓派相当于一台微型计算机，可连接电脑的局域网，通过局域网笔记本电脑上的远程桌面软件可以控制树莓派这台微型计算机，可实时操作这台树莓派微型计算机，在树莓派上编写视频拍摄程序，笔记本电脑上就可实时显示拍摄画面并进行拍摄视频的操作。控制四旋翼无人机飞行，拍摄道路裂缝的视频，传输至电脑进行分类检测。即可通过控制无人机飞行，来实现道路裂缝的分类检测。四旋翼无人机进行裂缝分类的工作状态，如图1所示。

图1 实验平台Fig.1 Experimental Platform

2.2 裂缝分类流程

通过四旋翼飞行器获取裂缝图像或视频，获取图像后对图像进行预处理，并分割裂缝目标区域，进一步提取裂缝骨架，提出了三类裂缝特征组成特征向量，采用了基于支持向量机分类器的学习算法。在机器学习中，支持向量机可以用于分类、回归、异常值或离群点检测。SVM 模型具有较好的学习和泛化能力且理论基础较扎实。起初SVM设计是为了解决二分类问题，对于线性可分的两类数据，支持向量机就是一条直线（对于高维数据点就是一个超平面），两类数据点的分割线有无数条，SVM 的目的就是通过学习找到最完美的这条直线或超平面。如图2 所示，将距离超平面最近的两个不同类别的样本点称为支持向量（support vector），构成两条平行于超平面的长带，二者之间的距离称为margin。学习的目标就是使得margin 最大，如此分类正确的确信度更高。数学上，通过优化目标函数：

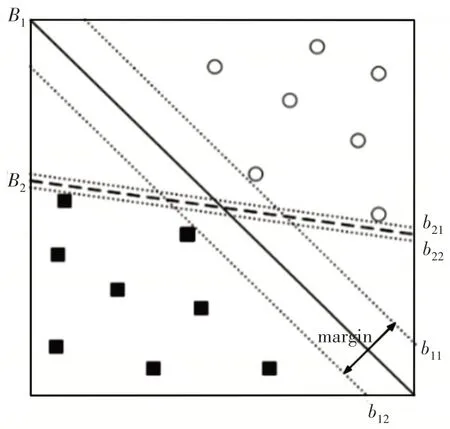
图2 SVM二分类Fig.2 SVM Dichotomy

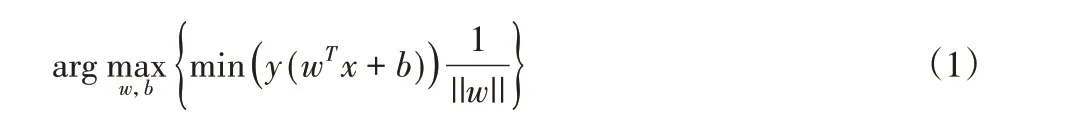
来确定最终的超平面wTx+b=0。其中，

表示样本点x到超平面的最短距离，式中：y—数据点标签，用1或-1表示。

SVM算法最初是为二分类问题设计的，当处理多类问题时，需构造合适的多类分类器，主要是通过组合多个二分类器来实现多分类器的构造，常见的方法由一对多法（One-Versus-Rest）和一对一法（One-Versus-One）。一对多法即是训练时将某个类别的样本归为一类，其他剩余样本归为另一类，这样k各类别样本就构造k个SVM，这种分类方法当训练样本增加时训练速度会急剧减慢；一对一方法是在任意两个样本之间设计一个SVM，因此需要设计k(k-1)/2 个SVM，这种方法针对于样本类别数较少的情况，分类速度快。在这里的实验中，裂缝的样本类别标签为四类，采用了一对一分类的方法训练多个二分类器，然后根据投票规则找到最终的预测分类标签。四类样本的分类决策过程，如图3所示。

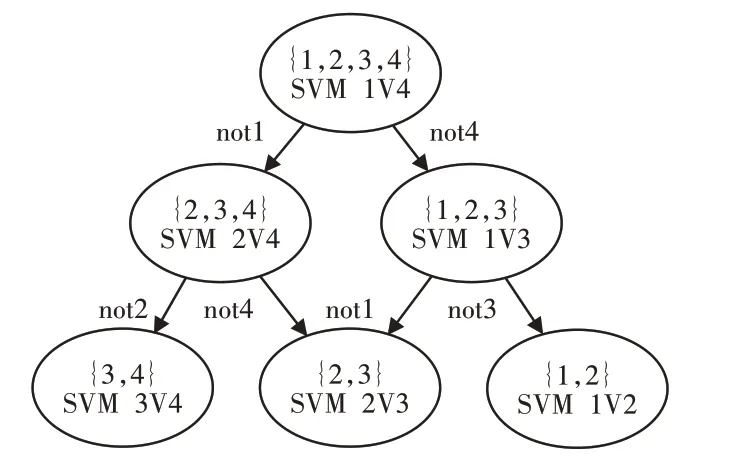
图3 四种样本分类Fig.3 Four Categories of Samples

为充分验证这里提出的三类特征的普遍适应性，采集了同类裂缝的不同形态图像，以纵向裂缝为例，如图4所示。

图4 纵向裂缝数据集Fig.4 longitudinal Crack Data Set

图像训练数据集选取了每类裂缝处于不同光照，拍摄高度与角度的图像，因此图像训练数据集具有一般性和典型性。实验共选取了1200张裂缝图像，这四类裂缝图像各300幅，将1200张裂缝图像分为四组，每组300张图像，其中，每类裂缝图像为75副。实验采用了留一法（记为K-CV）进行交叉验证，将图像样本集分为四组，每次选择其中一组样本作为测试集，剩余三组样本作为训练集，交叉实验共进行了四次，这样会得到四个分类模型，用这四个模型最终的测试集分类正确率的平均数作为分类器的性能指标。这样训练得到的结果相对有说服力，能准确反应裂缝测试集分类的正确率。这种交叉验证的方法也适用于这里样本数较少的情况。无人机视觉技术分类裂缝方法的流程，如图5所示。

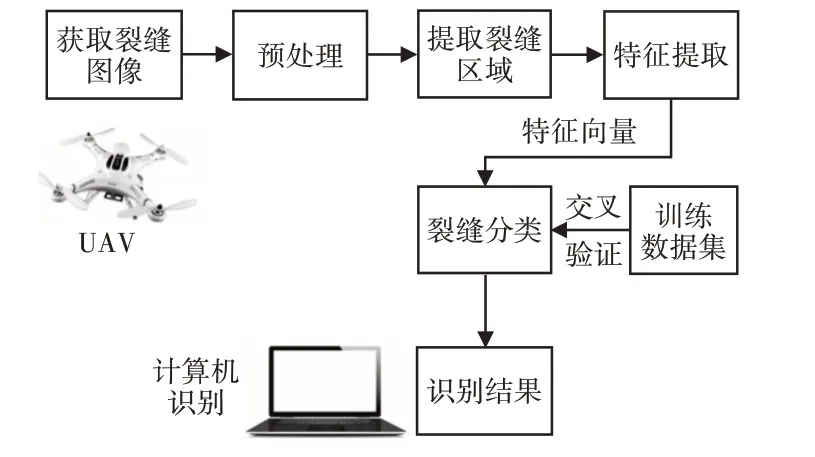
图5 裂缝分类流程图Fig.5 Flow Chart of Crack Classification

3 裂缝特征选取

图像经过预处理和裂缝目标区域分割及提取骨架后，提出了运用以下三类特征：裂缝投影的方向性特征Xd与Yd，裂缝骨架端点特征E，以及裂缝骨架与横纵网格交点数目比的特征R来对裂缝进行分类。

3.1 投影方向性特征

一副大小为M×N的裂缝数字图像，通过图像预处理转化为二值图像时，裂缝区域显示为白色，灰度值为1，非裂缝区域显示为黑色，灰度值为0。

分别统计裂缝区域沿X轴与Y轴方向上的灰度值为1的像素点的累积分布，即像素值f(i，j)=1的累计分布：

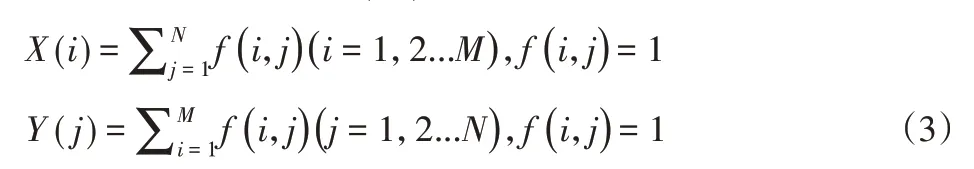
沿X轴方向与Y轴方向上灰度值为1的分布最大差值的计算公式如下：

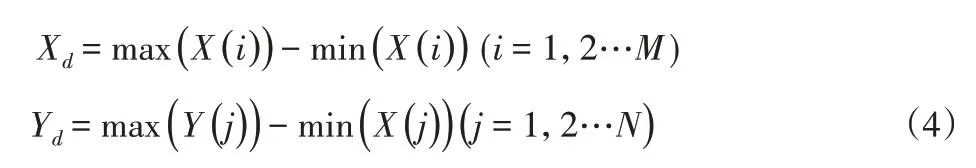
将沿轴向最大灰度分布差值Xd和Yd作为裂缝投影的方向性特征。

分别沿X轴方向与Y轴方向统计灰度值为1的像素点即裂缝区域的分布情况。反映了这四类裂缝的方向性特征，如图6 所示。中从左至右依次为裂缝原图，如图6（a）所示。裂缝的二值图，裂缝在X轴方向上的裂缝灰度分布图，裂缝在Y轴方向上的裂缝灰度分布图，图6（b），图6（c），图6（d）同图6（a）。

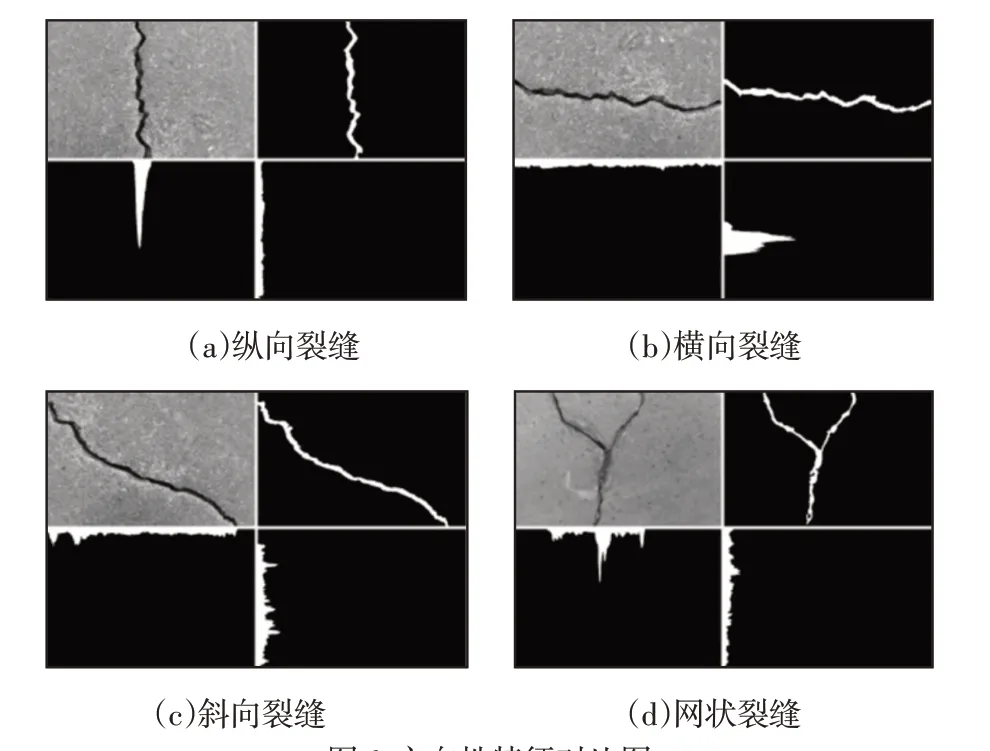
图6 方向性特征对比图Fig.6 Contrast Diagram of Directional Features

从上图6 对裂缝投影的方向性特征对比分析可知，图6（a）的纵向裂缝在X轴方向上灰度分布存在明显突起，而在Y轴方向上灰度分布较为平缓；图6（b）中在X轴方向上灰度分布较为平缓，而在Y轴方向上灰度分布存在明显突起；图6（c）中斜向裂缝和图6（d）中网状裂缝在X轴方向上与Y轴方向上的灰度分布较横向裂缝与纵向裂缝均无明显突起，分布较为平缓。因此选取Xd与Yd作为裂缝投影的方向性特征，它既可以将横向和纵向裂缝同斜向网状裂缝区分开，也可将横向裂缝和纵向裂缝进行区分。

3.2 裂缝骨架化端点数目特征

骨架［13］提取能剔除非裂缝的虚假信息，准确的显示出裂缝的形状特征，且根据形状特征可有效判别裂缝的类别。因此对裂缝图像进行预处理后提取了裂缝骨架。横向裂缝，纵向裂缝，斜向裂缝骨架一般为单一骨架，只有两个端点，而网状裂缝一般有多条骨架，具有明显的分支点，且网状裂缝骨架端点数一般大于两个。因此可根据裂缝骨架端点将网状裂缝同其他三类裂缝进行区分。

由上述理论分析设计裂缝骨架和端点提取算法对四类裂缝进行端点提取，如图7所示，每一类裂缝选取了两张典型的图像进行骨架端点提取的检测。结果显示不同形状的横向裂缝，纵向裂缝，斜向裂缝的端点数均为2，而网状裂缝的端点数至少为3。因此选取裂缝骨架的端点数E作为第二种分类特征，可将网状裂缝同其他三类裂缝进行有效区分。

图7 裂缝骨架的端点Fig.7 The End Point of Crack Skeleton

3.3 裂缝骨架与横纵网格交点数目比特征

由于裂缝的形成特性［10］，裂缝一般为线性的连贯区域，因此可将裂缝图像用16条水平方向直线进行等分，统计裂缝骨架与水平直线的交点数H；用16条竖直方向直线将裂缝图像进行等分，统计裂缝骨架与竖直方向直线的交点数V。将H与V的比值定义为R：

四类裂缝的网格划分提取交点的结果示意图，如图8所示。每一类的裂缝选取两张典型的裂缝图像进行骨架交点的特征分析。

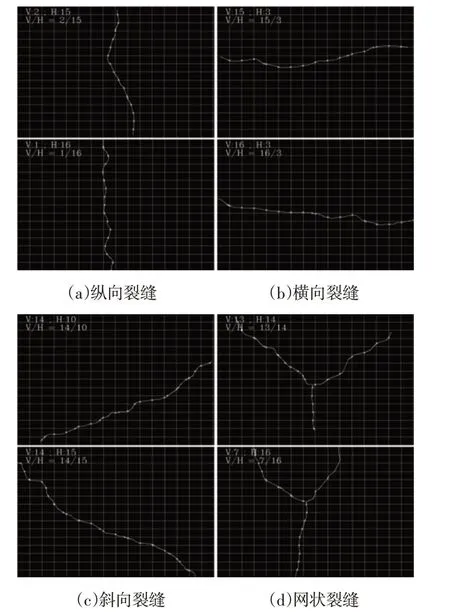
图8 骨架与网格的交点Fig.8 The Intersection of The Skeleton and The Grids

图8数据依次显示了骨架与竖直网格交点数目V，骨架与水平网格交点数目H，以及H与V的比值R。观察纵向裂缝的网格交点特征可知，纵向裂缝的竖直交点数V远小于水平交点数H，且R值远小于1；横向裂缝的竖直网格交点数目V远大于水平网格交点数目H，且R值远大于1；斜向裂缝的竖直网格交点数V与水平网格交点数H接近，且横纵网格交点数目比值R约为1；网状裂缝的竖直网格交点数V与水平网格交点数H接近，比值约为1。

综上分析可知，裂缝骨架与横纵网格交点数目比值R可将横向和纵向裂缝同斜向和网状裂缝进行区分，且R能将横向裂缝与纵向裂缝进行区分，区分度较高。

3.4 裂缝特征分析

将这四类裂缝进行分类的三种特征分析表格参数，如表1所示。

表1 三种特征分析Tab.1 Three Feature Analyses

4 分类效果与对比实验

4.1 裂缝分类识别图

三类特征进行裂缝分类的识别效果图，如图9所示。

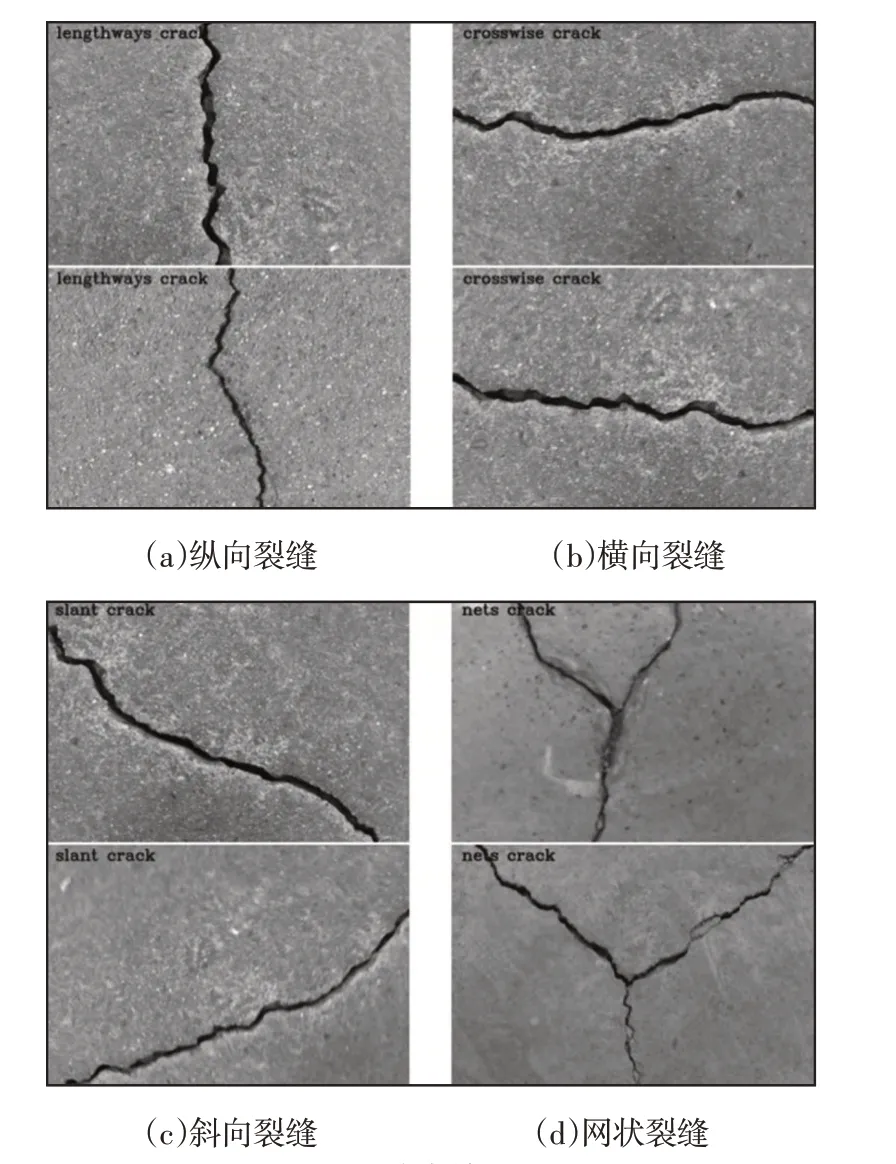
图9 分类效果图Fig.9 Classification of The Rendering

在训练集图像数据进行学习之后，对测试集图像进行分类测试，分类正确率结果，如表2所示。结合图9分类识别图分析可知，选取的裂缝投影方向性特征Xd与Yd，裂缝骨架端点特征E，及裂缝骨架与横纵网格交点数目比特征R能较好的将这四类裂缝进行分类，且具有较高的正确率。

表2 裂缝分类正确率Tab.2 Correct Rate of Crack Classification

4.2 特征对比试验及分析

为验证文中提出特征的优越性，进行了特征对比试验。对比实验选取了裂缝常见的分布区域面积特征［11］Area：

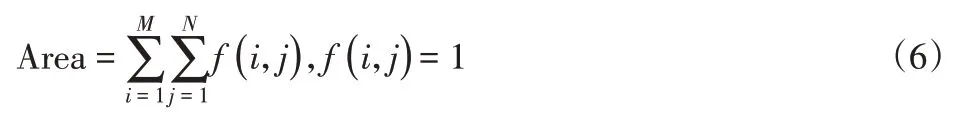
面积特征Area表示裂缝分布的区域面积。它一般用来将网状裂缝同其他三类裂缝进行区分。保持裂缝的方向性特征Xd和Yd，裂缝骨架与横纵网格交点数目比R特征不变，将这三类特征对相同的图像数据集进行实验测试，如表3所示。

表3 对比试验的结果Tab.3 Classification Results ofComparative Experiments

结合表2与表3的实验正确率数据对比分析可知，裂缝区域面积特征Area对于将斜向裂缝与网状裂缝的分类正确率较低，只有65.33%，66.67%的正确率。分析可知斜向裂缝与网状裂缝的裂缝面积无较大的区分性，斜向裂缝与网状裂缝的面积较为接近，易造成混淆，所以裂缝区域面积特征Area对于网状裂缝与斜向裂缝的分类正确率偏低。

对比表2 与表3 的横向裂缝与纵向裂缝分类正确率可知，分析表2 与表3 中的横向裂缝与纵向裂缝分类正确率，正确率均较高说明裂缝投影的方向性特征Xd与Yd及裂缝骨架与横纵网格交点数目比特征R可较好的将这横向裂缝和纵向裂缝进行分类，对比表2 与表3 中的斜向裂缝与网状裂缝分类正确率可知，裂缝骨架端点特征E可较好的将斜向裂缝和网状裂缝进行区分，进一步说明了这里提出的这三类特征进行裂缝分类的优越性。

5 结论

搭建了相应的实验平台，运用四旋翼无人机视觉检测技术进行裂缝分类的检测实验，检测了提出此法的可行性。这里采用了支持向量机分类器的方法对裂缝进行分类，提出了裂缝投影的方向性特征Xd与Yd，裂缝骨架端点数目特征E，及裂缝骨架与横纵网格交点数目比特征R作为裂缝分类的特征依据。实验结果表明提出的这三类特征能将四类裂缝进行有效区分，分类识别正确率高。并进行了特征选取的对比实验，进一步说明文章提出的三类分类特征的优越性。