基于多尺度卷积神经网络的滚动轴承智能诊断算法
2022-05-19古天龙孙镇海1宾辰忠
古天龙,孙镇海1,,宾辰忠,常 亮
(1.桂林电子科技大学,广西 桂林 541004;2.广西可信软件重点实验室,广西 桂林 541004)
1 引言
现代工业中,机械装置故障诊断是安全生产必不可少的环节。滚动轴承是旋转机械装置中最为常用的部件,一旦轴承发生故障可能导致严重事故甚至造成巨大经济损失和人员伤亡。现主流方法是在轴承振动加速度时序信号进行分析与监测[1]。深度学习模型借助多层非线性映射能力更好的逼近复杂函数,往往比传统方法有着更好的诊断精度。以往的研究表明,诊断精度在很大程度上取决于提取特征过程。因此,特征的抽取是故障诊断领域中一个重要研究方向[2]。
2 相关工作
机器学习技术早已应用于轴承故障诊断中。如文献[3]提出了基于LMD 和SVDD 的滚动轴承健康状态评估算法。而卷积神经网络(CNN)一直是深度学习领域炙手可热的算法之一。许多学者提出优秀的卷积神经网络经典结构,但是由于CNN与一维振动信号不兼容,导致这些模型并不能直接运用到故障诊断领域。文献[4]提出以振动信号小波时频图作为二维卷积神经网络模型输入。文献[5]开发了一种信号到图像的转换方法,使用2DCNN取得优异的诊断精度。上述算法通过一些方法将一维数据转换为二维数据,振动信号作为一维时序信号转换为二维数据保证不了转换后数据关联性是否遭遇破坏。因此,使用原始一维信号直接作为输入数据是更为合理的诊断方案。
迄今为止,一维CNN 对时序信号处理已有了阶段性成果。文献[6]提出了一维多渠道CNN模型,应用于时序性序列的处理,但是多元的时序信号意味着多种传感器。文献[7]中,作者提出了WDCNN 模型,利用深度卷积网络诊断方法;紧接着文献[8]在WDCNN基础上引入Drop-out卷积核方法,使模型泛化能力更上一层楼。而文献[9]中,作者提出了一个自适应故障诊断算法,使用双层卷积网络,更为侧重算法的鲁棒性。
综上,现阶段一维CNN 诊断领域通常存在如下几处存在不足:
(1)需要大量数据支持,未考虑极端环境的存在;(2)忽略振动信号固有特征,仅当作普通时序性信号处理。因此,这里更为关注使用小数据集获得更好效果,同时还兼顾模型的适应能力。这里的主要创新点如下:①利用多尺度卷积层作为特征提取的方法;②考虑轴承振动信号的固有特征,利用轴承转速,故障尺寸等参数确定模型参数,结合实际情况解决实际问题;③将BN网络引入多尺度卷积神经网络智能诊断算法中;④引用“数据增强”概念,大幅扩充样本数量。
3 方法介绍
3.1 一维卷积神经网络
卷积神经网络(CNN)由卷积层,池化层与分类层组成。本质上CNN是通过一系列方法将庞大的数据量不断减少并保留数据主要特征。核心功能介绍如下:(1)局部感受野:采用CNN时,每个神经元只感受局部信息,最后将所有感受野得到不同振动信号的局部神经元进行筛选整合以获得整体特征信息,这样不仅减少的计算量也增加了神经网络的可靠性;(2)权值共享:对一维振动信号使用多种滤波器进行卷积获取多种特征向量,这时候每一个局部感受野参数共享,不仅可以进一步减少计算量,还能够学习到更多样的信号特征。
3.2 批归一化
批归一化(Batch Normalization)[10]是由Google公司提出应用于神经网络训练.目的在于减少训练方差的偏移,代替一些正则化处理方法甚至比它们更为有效。通常在卷积层之后或在激活单元之前添加。
增加模型的泛化能力,也就是保证训练集与测试集数据的分布情况相似。BN算法在卷积层之后对激活函数进行归一化,减小数据偏移误差。在文献[11]中也验证了该方法能够使数据混杂地更为均衡,减小了数据集之间的差异性。
4 MSCNN智能诊断算法
模型包括三部分:数据处理层、特征提取层和诊断分级层。具体细节将在下面展开。
4.1 数据处理层
数据处理层的目的是对原始振动信号数量上的扩充。在诊断过程中,通常采集到的振动信号是属于长时间序列。它的建模和挖掘特征在数据量上很难满足机器学习任务对数据量的要求。因此模型引入“数据增强”概念:将时间序列分割成若干个较短的时间序列,对训练样本进行重叠切片。“数据增强”示意图,如图1所示。步长为每一个样本相隔的距离。

图1 “数据增强”示意图Fig.1 Diagram of the Data Augmentation
4.2 特征提取层
特征提取层利用深层多尺度卷积实现振动数据的特征信抽取。在第一层卷积阶段,如图2所示。模型以经数据处理层后的样本数据作为输入,再利用尺寸相异的4种不同卷积核并行提取不同跨度的时序信号分别对振动信号进行卷积操作。为了保证模型获取最全面的特征信息,最大的卷积核长度设为轴承一整圈检测点数,确保每一次卷积覆盖了轴承一整圈振动信号,获取振动信号全局特征,减少特征的缺失;然后结合长度大于故障区域采集点的卷积核获取局部特征,确保故障区域异常数据在训练过程中得到较大的权重;最后选择2种在长短卷积核尺寸之间的卷积核,增加模型的宽度,使模型提取到的特征更为细腻,补充特征中振动信号前后纽带关系。不同卷积核得到不同的轴承特征向量,一定程度摆脱了对数据量的依赖。定义模型输入数据为S=(x1,x2,x3,…)卷积公式可描述为:

图2 MSCNN框架图Fig.2 Structure of the Proposed MSCNN Model
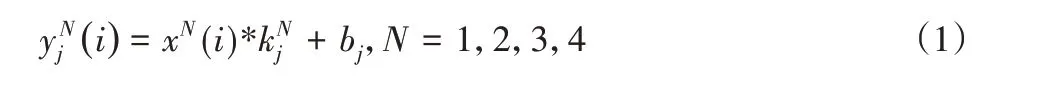
式中:Sj—输入的振动特征向量;
N—不同尺度空间;
bj—第j个卷积核的权重与偏置;
xN(i)—第N维度空间内第i个局部区域。
模型在卷积层数据激活之前这里引入BN算法,减小数据偏差,增强模型泛化能力。
这里使用线性整流函数ReLU(Rectified Linear Unit)作为激活函数,池化方式为Max-Pooling。
其数学公式描述如下:

由于模型采用多次卷积的方法并使用数据加强技术,因此模型在卷积过程中误差主要来源于卷积层参数误差造成估计均值发生变化,而这种情况下,Max-Pooling 层对输入特征执行局部Max 操作,以减少参数,获得位置不变的特征更适合面对。因此池化方法选择Max-Pooling。最终得到4 种不同维度空间特征向量。
最大池转换描述如下:

W—池化宽度;
获取到不同的特征向量后,可以选择对不同特征向量进行深度提取,也可以选择继续利用尺寸相异卷积核对它们分别进行特征提取,这里选择后者。对各个空间特征向量处理方法与上述处理原始信号方法相同最后输出多个特征向量。
4.3 诊断分级层
诊断分级层的作用在于整合所有特征向量,并利用分类函数进行健康状态分级。这里使用首尾相连的方法实现对特征提取层得到的零散特征向量拼接操作,得到一维特征向量。
分类步骤由两个全连接层完成,输入层为拼接整合后的一维向量,中间层为过渡层,目的为了减少全连接的训练参数,输出层神经元个数为故障等级数目,最后利用Softmax分类函数实现的诊断分级,函数公式如下:

4.4 模型训练方法
这里使用softmax输出概率分布与目标分别之间的交叉熵,考虑到这里模型使用数据加强,BN算法可代替正则项,因此这里loss函数中并没有正则项。设为p(x)目标分布,q(x)为预估分布,loss函数公式如下:
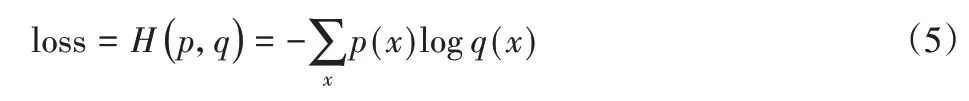
随机梯度下降法(SGD)尽管近些年逐渐被Adam优化算法取代但仍不失为机器学习领域中是最为经典的优化算法之一。该方法通过在小批量数据上计算损失函数的梯度而迭代地更新权重与偏置项。
SGD公式如下:

式中:wk—第k次更新迭代;
λk-1—学习率;
f—损失函数。
在文献[12]指出Adam虽然在训练初期优于SGD,但在收敛后性能,泛化能力,稳定程度却都不如SGD优秀。
5 实验
凯斯西储大学(Case Western Reserve University)实验室提供了正常和故障滚珠轴承的加速度振动信号数据。该数据集含有单点驱动端和风扇端故障轴承在0hp,1hp,2hp,3hp不同马力下的加速度数据。对于故障轴承,使用电火花加工技术对轴承外圈、内圈、滚动体制造直径为7、14、21mils的单点缺陷。这里选择验证MSCNN算法时使用在3个缺陷部位的3种缺陷轴承加上正常轴承共十种类型轴承数据。
5.1 参数实验
从轴承数据集描述中得到数据采集的频率和转速,推断出轴承每圈采集的数据数量约为400;由单点缺陷尺寸与轴承外圈直径得知最少需要4个测试点位覆盖整个缺陷点。这里选择每个样本2000个数据点,保证每个样本都覆盖轴承一整圈测试数据且具备多样性;第一层卷积层中,全局特征卷积核尺寸为400,局部特征卷积核为20。由于这里卷积核较宽,若在此基础上使用深度卷积网络则模型参数数量倍增而导致训练效果不佳。因此这里将采取双层卷积层模型。
为了验证不同配置感受野神经元对实验影响,在本小节实验中每种故障情况选择500个训练样本,每组实验20次,迭代次数20,学习率为0.001,drop-out概率为0.3,batch大小为10(下文实验中未明确说明的实验参数与本次实验相同)。评价标准为20组实验平均测试集准确率。不同参数的实验结果,如表1所示。

表1 不同参数的实验结果Tab.1 Experimental Results of Different Parameters
结合上表数据,在这几组实验中已经充分证明利用振动信号固有特征进行模型参数的选择是切实可行的方法。这里选择第一层卷积层卷积核尺寸分别为400,200,100,50;第二层卷积层卷积核尺寸分别为32,16,8,4参数方案。
5.2 小样本实验
这里模型致力于摆脱轴承健康诊断对大量数据的依赖性。为了验证效果是否符合预期,在本小节实验里这里将与WDCNN等经典模型进行对比实验研究。所有训练的数据集,实验参数等都是相同的,综上测试集正确率依然不失为最佳评估标准。实验结果,如表2所示。

表2 不同数量的实验数据的实验结果Tab.2 Experimental Results Using Different Amount of Experimental Data
表2中可以清晰看出,在模型的精度方面,三种模型随着训练样本的增加,准确率上升。在500个样本数量时MSCNN准确度基本达到100%,远远比其他模型精度要高。虽然在样本逐渐增多的情况下WDCNN算法诊断精度不断地提升,但是在数据量依赖程度来说,MSCNN算法模型是更加可靠地。
这里为了进一步证明在小样本数据中MSCNN是否有着绝对的优势,这里上述方法在样本数据为500 时的训练过程罗列出来,如图3所示。测试集准确率略高于训练集,表明实验效果未发生过拟合现象。可以清晰的看出,MSCNN在不管是准确率上,还是收敛速度上MSCNN 都有着不错的性能。样本数据量为500,在机器学习领域不可谓大数据集。由此可见这里方案在减少诊断算法数据依赖的研究方面是确实可行。
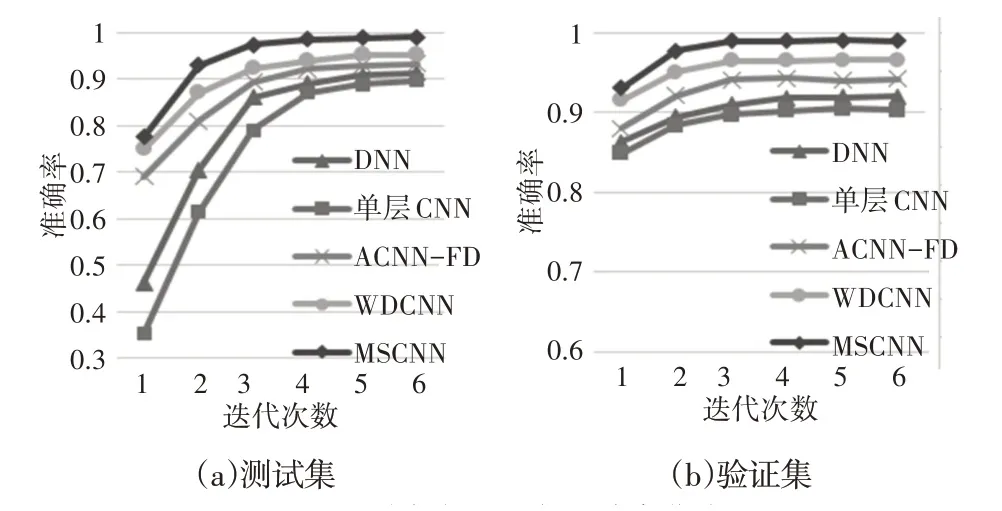
图3 训练集与测试集准确率曲线Fig.3 Curves of Accuracy of Training and Testing Datasets
5.3 泛化能力实验
在实际工作中,机械系统的工作环境十分复杂,干扰因子数不胜数。在本小节中,这里通过不同的负载数据交叉实验验证MSCNN模型泛化能力。实验过程中依然采用0马力数据作为训练集进行模型训练,但是测试集使用换为1hp,2hp,3hp数据。测试集数据采用与训练集相同的10种分类故障等级。依旧以测试集准确度为评估标准,实验结果,如图4所示。
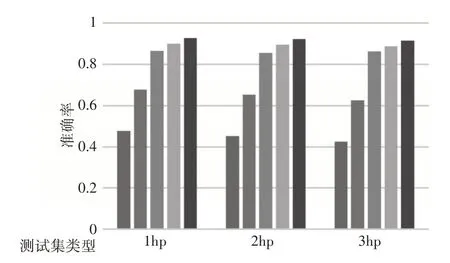
图4 不同数据集性能实验Fig.4 Performance Experiments on Different Data Sets
根据上图可以看出交叉实验中,在此3种实验条件下,诊断精度在90%以上仅有MSCNN。说明在交叉实验中,一般机器学习模型是无法适应数据集的变化。总的来说,本实验证明了MSCNN能够清晰的辨别的故障特征。
6 总结
针对现有的诊断方法缺失对小ss样本数据的处理能力,这里提出了一种一维多维度空间卷积神经网络故障智能诊断模型MSCNN,保证诊断精度的同时也具备一定的泛化能力。
实验证明MSCNN在各种工作条件下都能获取精确的诊断结果,特别在小样本数据情况下,MSCNN有着超群地精度。
该方法优点总结如下:
(1)可以直接作用于原始信号,有一定地实时监控能力;
(2)多维度空间卷积层拓宽与深化了神经网络,能够更好地学习振动信号特征,减少了对数据地依赖并增加了模型地泛化能力;
(3)结合振动信号固有特征确定模型参数,提高模型针对特定问题的诊断精度;
