旋转冲击载荷下组合密封的敏感参数研究*

李渭亮 李林涛 程飞龙 石昌帅

(1.中国石化西北油田分公司石油工程技术研究院 新疆乌鲁木齐 830011；2.中国石化缝洞型油藏提高采收率重点实验室 新疆乌鲁木齐 830011;3.西南石油大学机电工程学院 四川成都 610500)

随着石油钻井深度不断增加，受深部高研磨性地层、高硬度地层、高温高转速等因素的影响，常规螺杆钻具面临损坏严重、破岩效率低及钻速慢等问题，已经不能满足现场钻井提速需要，从而提出了可提高机械钻速的冲击螺杆钻具[1]。冲击螺杆钻具在传递扭矩的同时，可以产生高频低幅轴向冲击，能够有效提高机械钻速，如图1所示[2]。然而，随着钻探深度的增加，井底温度不断升高，在高温、往复运动耦合作用下冲击螺杆钻具传动轴总成密封极易失效，限制了冲击螺杆钻具的推广应用[3]。因此研究高温、高转速和往复运动耦合作用下传动轴总成密封特性及参数敏感性具有重要工程价值。

BOWER[4]用实验分析了外部载荷作用O形密封圈压缩量的影响规律,得到压缩量加大载荷速度变小。RODRIGUEZ和MARKOVITCH[5]分析各种影响参数对泄漏的影响规律。KIM[6]通过数值仿真方法分析了O形密封圈在V形槽中静密封性能，得到其应变、应力情况。CUI等[7]通过Abaqus研究了二维轴对称模型Y形密封圈静密封，得到Mises应力、应变和接触应力规律，得出预压缩状态最大应力位于上唇和下唇交界处，压力增大，应力增大，最大接触压力集中于Y形密封圈与往复杆和密封槽底部接触区域。GU等[8]通过有限元方法研究了气动灭火炮密封弹壳橡胶密封圈表面仿生凹坑静密封性能，得到压缩量2.5 mm时，橡胶密封圈的最大接触压力集中于密封圈两侧，仿生凹坑中间位置接触压力较小，密封边缘等效应力较大。BHAUMIK等[9]通过有限元方法研究U形密封圈静密封性能，分析了速度和压力对其密封性能的影响。NIKAS[10]使用数值仿真方法分析了二维轴对称模型往复运动密封圈润滑和泄漏情况。MAZZA和BELFORTE[11]分析了二维轴对称模型往复运动密封圈摩擦力情况。AZZI等[12]分析了速度对往复运动X形密封圈摩擦特性的影响。YOKOYAMA等[13]通过数值仿真方法研究了二维轴对称模型O形密封圈静密封特性。然而国内外主要集中于普通螺杆钻具研究，对冲击螺杆及其密封研究较少。

本文作者对冲击螺杆钻具选择不同的密封圈，基于主密封面接触压力，对影响组合圈密封特性的相关参数进行数值仿真模拟，研究了摩擦因数、O形圈直径、碳纤维含量和往复速度等参数对组合圈密封性能的影响规律。由于密封圈的系统参数、结构尺寸参数和材料参数等数值较小，但与工具密封压力的比值较大，因此称为敏感性参数，通过该类参数的研究为冲击螺杆钻具密封圈的选型及使用提供指导和参考。

1 热老化密封圈的本构模型研究

为了获得近似氢化丁腈密封圈在井下工作状态的力学性能，并建立可靠的有限元模型，需要建立老化后的氢化丁腈试样的本构模型。根据ASTM标准和工作环境，设置25 ℃(室温)、70 ℃、130 ℃3组老化温度，对哑铃状的氢化丁腈橡胶试样进行老化处理。将老化后的试片以0.01 mm/s加载速度进行单轴拉伸试验，获得橡胶试样应力-应变数据，试验设备如图2所示。

文中以氢化丁腈橡胶O形密封圈为研究对象,不考虑橡胶材料蠕变、应力松弛，橡胶材料看作是一种各向同性、不可压缩的超弹性材料[14]。

研究表明，Yeoh本构模型能准确描述氢化丁腈橡胶的力学行为，其公式如式(1)所示。

(1)

式中：λ为应变(单位为1)；σ为应力，MPa；C10、C20和C30为Yeoh模型的参数，MPa。

将不同温度橡胶拉伸试验得到的应力-应变结果处理为Yeoh本构模型，各参数如表1所示。

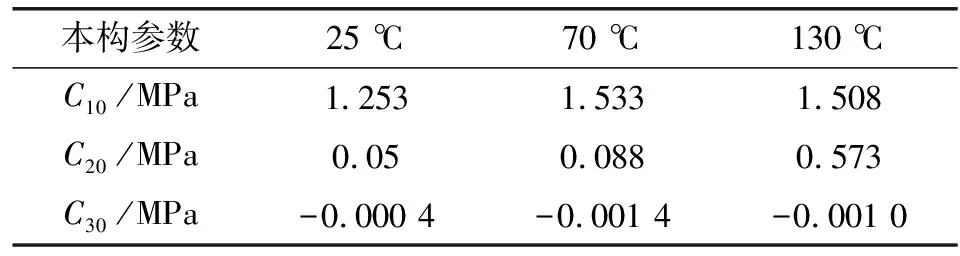
表1 不同温度下Yeoh本构模型的参数

2 有限元模型

组合圈仿真模型由槽、轴、滑环和O形圈组成，O形圈截面尺寸5.7 mm，摩擦因数0.04，滑环及槽尺寸参考车氏密封TB4-IB120X5.7，轴与滑环作用形成的接触面为主密封面，定义为CS1；O形密封圈与槽底面形成的接触面为次密封面，定义为CS2，除橡胶以外参数见表2。

表2 密封结构使用材料及力学参数

对有限元模型进行网格划分，轴、槽弹性模量高于O形圈，对网格划分要求不高，因此只研究O形圈的网格无关性，其有限元网格如图3所示。

为分析网格尺寸大小对有限元模拟运算结果的影响，对O形圈划分网格尺寸分别为0.35、0.45、0.55、0.65、0.75进行仿真计算。网格尺寸越小，网格数越多，计算时间越长。图4(a)所示为不同网格无关性验证曲线，可以看出网格尺寸为0.35和0.45，即网格数量为41 360和37 600时Mises差值较小。文中选择网格尺寸为0.45进行后续计算，不仅加快了仿真效率，而且计算结果比较准确。

根据KIM等[15-16]研究了O形密封圈的实验结果，建立与其相同尺寸、压缩率和边界条件的三维有限元模型，并仿真计算得到不同压力下的接触压力变化规律，如图4所示。仿真结果与实验结果变化规律基本上相同，误差小于8%，证明了文中所运用的三维有限元模型仿真方法比较可靠。

3 静密封和动密封特性研究

3.1 静密封特性研究

静态密封是动态密封的前提，静态重点分析密封圈预压缩和受流体压力时的密封特性，而密封圈在使用过程会发生失效和泄漏，因此要分析影响密封性能的接触压力和失效的Mises应力情况[17]。

组合圈预压缩Mises应力分布如图5(a)所示，其O形圈高应力位于中上部，呈左右对称，而滑环高应力位于中部和左、右下角，左下角略大于右下角是由于右侧面槽挡住使右侧滑环变形小于左侧。组合圈预压缩接触压力分布如图5(b)所示，组合圈高接触压力区集中于滑环外圆面和内圆左右下角。

组合圈静密封Mises应力分布如图5(c)所示，高应力位于滑环中部和右侧面，高应力区域容易发生失效。静密封接触压力如图5(d)所示，高接触压力集中于滑环内圆中部。

3.2 动密封特性研究

动态密封仿真研究分左行程和右行程分析，左行程、右行程以往复速度为0.3 m/s和转速150 r/min进行仿真计算。

图6(a)和(b)所示分别为组合圈左行程与右行程Mises应力分布，可见其高应力集中于滑环中部和右侧面。图6(c)和(d)所示分别为组合圈左行程与右行程接触压力分布，可见左行程和右行程O形圈存在3处高接触压力区，高接触压力区位于密封圈外圆面、内圆面及右侧面，右行程接触压力高于左行程可能是由于流体压力方向与运动方向相同；组合圈左行程和右行程接触压力分布相同，其高接触压力区位于滑环内圆中部。

4 密封敏感参数研究

为了研究密封圈的系统参数、结构尺寸参数和材料参数中与密封压力比值较大的敏感参数对组合圈密封特性的影响，通过有限元方法模拟研究摩擦因数、O形圈直径、碳纤维含量和往复速度等对Mises应力、接触压力的分布和大小影响情况[18-19]。

4.1 摩擦因数的影响

摩擦因数是影响密封圈密封特性的主要参数，在有限元模拟中摩擦因数取值分别为0.01、0.02、0.03、0.04，其余参数为往复速度0.3 m/s、转速150 r/min、压缩量0.45 mm、滑环厚度0.5 mm、流体压力10 MPa。

图7所示为不同摩擦因数下CS1密封面接触压力模拟计算结果。由图7(a)可知，左、右行程摩擦因数为0.01、0.02、0.03时，接触压力变化规律相近，摩擦因数为0.04时接触压力波动幅度较大；接触压力波动幅度基本随着摩擦因数的增大而增大。由图7(b)可得，左、右行程接触压力平均值随着摩擦因数的增大而减小，说明摩擦因数增大密封性能减弱，但仍然大于流体压力；接触压力与摩擦因数呈非线性关系变化。

图8所示为不同摩擦因数下滑环Mises应力模拟计算结果。由图8(a)可知，左、右行程摩擦因数小于等于0.03时Mises应力规律一致且波动程度较小，摩擦因数为0.04时Mises应力呈现出大幅度波动；左行程应力随摩擦因数的增加而增大，右行程应力随摩擦因数的增加而减小。由图8(b)可知，左行程应力平均值大于右行程，左行程应力和摩擦因数呈正比例线性关系，右行程随摩擦因数增大应力线性减小。

图9所示为不同摩擦因数下O形圈Mises应力模拟计算结果。由图9(a)可知，左、右行程在摩擦因数为0.01～0.03时的应力变化规律基本相同，且基本保持稳定；摩擦因数为0.04时应力变化规律出现较大波动。由图9(b)可知，左、右行程Mises应力平均值随摩擦因数的增大而增大，基本呈线性增长，在0.01～0.04摩擦因数范围内右行程应力增长率较快，相同摩擦因数下右行程应力高于左行程。

4.2 O形圈直径的影响

O形圈在加工中可能出现直径偏差，这也会对密封圈密封特性造成影响。在有限元模拟中O形圈直径分别取5.5、5.6、5.7 mm，流体压力取5 MPa，压缩量取0.55 mm，其余参数与上节相同。

图10所示是不同O形圈直径下CS1密封面接触压力模拟计算结果。由图10(a)可知，接触压力随O形圈直径增大而增大，不同O形圈直径下接触压力变化规律基本相同，左行程接触压力平均值低于其右行程，总体动密封有效。由图10(b)可知，接触压力平均值随O形圈直径变化规律均呈二次线性关系，而且密封圈直径越大，接触压力变化率越大，整体上左行程接触压力低于右行程。

图11所示为不同O形圈直径下滑环Mises应力模拟计算结果。由图11(a)可知，左、右行程滑环应力值随O形圈直径的增加而增大，Mises应力几乎无波动；左、右行程Mises应力差值基本相等，左行程应力略高于右行程。由图11(b)可知，左、右行程Mises应力平均值随O形圈直径增大而呈非线性增大，而应力均值差值不随密封圈直径变化而变化；直径为5.5～5.6 mm时应力增长速度小于直径为5.6～5.7 mm时，右行程应力低于左行程。

图12所示是不同O形圈直径O形圈Mises应力模拟计算结果。由图12(a)可知，左、右行程O形圈直径增大，O形圈应力及应力差值逐步增大，应力几乎无波动，左、右行程应力差值基本相等，左行程应力稍低于右行程。由图12(b)可知，左、右行程Mises应力平均值随着密封圈直径的增加而增大，呈现非线性增长，直径为5.5～5.6 mm时应力增长率小于直径为5.6～5.7 mm时，右行程应力略高于左行程。

4.3 PTFE中碳纤维含量的影响

基于王哲[20]的结论，向纯聚四氟乙烯材料中添加不同含量碳纤维，得到其力学特性参数见表3。

将表3中参数导入有限元模型，取流体压力为5 MPa，其余参数与上节相同，进行有限元模拟分析。

表3 不同碳纤维质量分数下聚四氟乙烯力学特性参数

图13所示是不同碳纤维质量分数下CS1密封面接触压力模拟计算结果。由图13(a)可知，右行程接触压力呈大幅度波动变化，不同碳纤维质量分数下接触压力变化规律相同；碳纤维含量增加接触压力及接触压力差值增大，最大接触压力大于流体压力5 MPa，动密封有效。由图13(b)可知，左、右行程接触压力平均值及差值随着碳纤维质量分数的升高而增大，左行程接触压力一直大于右行程，同时右行程接触压力均高于流体压力5 MPa，能实现密封。

图14所示为不同碳纤维质量分数下滑环Mises应力模拟计算结果。由图14(a)可知，左、右行程应力呈波动变化，右行程波动幅度大于左行程；左、右行应力变化规律并不一样，但不同碳纤维质量分数下应力变化规律一样，且随碳纤维质量分数增加应力值逐渐增加；不同碳纤维质量分数下左行程应力比右行程高。由图14(b)可知，碳纤维质量分数升高，左、右行程Mises应力平均值增大，然而应力差值基本不随碳纤维质量分数改变而变化，左、右行程应力基本呈线性变化，左行程应力大于右行程。

图15所示为不同碳纤维质量分数下O形圈Mises应力模拟计算结果。由图15(a)可知，左、右行程应力呈波动规律变化，波动幅度不大；不同碳纤维质量分数下应力变化规律基本相同。由图15(b)可知，随碳纤维质量分数增加，左、右行程Mises应力平均值增大，而应力差值随碳纤维质量分数增加而减小，右行程应力高于左行程。

4.4 往复速度的影响

在有限元模拟中往复速度分别为0.1、0.2、0.3、0.4 m/s，其余参数和上一节相同。

图16所示是不同往复速度下CS1密封面接触压力模拟计算结果。由图16(a)可知，左、右行程接触压力呈波动状态，不同往复速度下接触压力变化规律相同，最大接触压力均高于流体压力8 MPa，动密封可靠。由图16(b)可知，左行程接触压力平均值随往复速度的增大基本呈现逐渐变小趋势，而右行程接触压力则变大；右行程接触压力呈线性变化，左、右行程接触压力差值逐渐增大，右行程接触压力均高于左行程。

图17所示为不同往复速度下滑环Mises应力模拟计算结果。由图17(a)可知，左、右行程应力呈波动变化，不同往复速度下应力变化规律基本相同。由图17(b)可知，随着往复速度增大，左、右行程Mises应力平均值变化规律相反，左行程增大而右行程减小；左、右行程应力基本呈线性变化，应力差值逐渐增大，左行程应力高于右行程。

图18所示为不同往复速度下O形圈Mises应力模拟计算结果。由图18(a)可知，左、右行程应力是呈现波动变化，往复速度增大应力基本呈增大趋势。由图18(b)可知，左、右行程Mises应力平均值及差值随着往复速度增加基本逐渐增大，呈非线性变化；左行程在0.2～0.3 m/s之间变化率最小，在0.3～0.4 m/s之间变化率最大，而右行程在0.2～0.3 m/s之间变化率最大，右行程应力高于左行程。

5 结论

为了延长冲击螺杆钻具的使用寿命，研究高温、高转速和往复运动耦合作用下传动轴总成密封特性及参数敏感性，探讨摩擦因数、O形圈直径、碳纤维含量和往复速度等参数对组合圈密封性能的影响规律。得到结论如下：

(1)预压缩状态下，摩擦因数增大，CS1、CS2密封面接触压力及O形圈、滑环von Mises应力增大；静密封状态下，摩擦因数增大，CS1及CS2接触压力减小，滑环von Mises应力增大，对O形圈应力影响较小；动密封状态，左、右行程摩擦因数为0.01、0.02、0.03时，接触压力呈现相似的变化规律，波动幅度较小，摩擦因数为0.04时呈现异常变化规律且波动幅度较大，左、右行程接触压力均值随着摩擦因数的增大而减小，说明密封性能减弱，摩擦因数增大左行程滑环von Mises应力增大而右行程应力减小，但左、右行程O形圈应力都增大，因此综上可得推荐摩擦因数小于0.04较为合理。

(2)预压缩状态，O形圈直径增大CS1、CS2密封面接触压力及O形圈、滑环von Mises应力增大；静、动密封状态CS1、CS2密封面接触压力及O形圈、滑环von Mises应力随O形圈直径、弹性模量及碳纤维含量增大而增大。

(3)右行程CS1、CS2密封面接触压力平均值比左行程大，左行程接触压力均值随往复速度的增大基本呈减小趋势，而右行程则相反，左、右行程接触压力均值及应力均值差值随往复速度的增大而增大。