基于回归分析模型的乙醇偶合制备C4烯烃工艺研究

康佳 吴海燕 袁亚硕

摘要：C4烯烃广泛应用于化工产品及医药的生产，乙醇是生产制备C4烯烃的原料。本文首先探究每种催化剂组合下乙醇转化率、C4烯烃的选择性与温度的关系，进一步运用线性/非线性回归的知识，建立回归模型来拟合其之间的关系，分析350℃时某一催化剂条件下不同时间中的测试结果。然后，探究不同催化剂组合以及温度对于乙醇转化率和C4烯烃选择性大小的影响，对四个变量之间的关系进行分析。最后建立多重对应分析模型，将四种数据能够从视觉上直接展示出来。

关键词：多重对应分析模型;SPSS;回归分析

1 引言

C4烯烃广泛应用于化工产品及医药的生产，乙醇是生产制备C4烯烃的原料。在制备的过程中，催化剂的组合（即：Co负载量、Co/Sio2和HAP装料比、乙醇浓度的组合）与温度对C4烯烃的选择性和C4烯烃收率将产生影响。因此通过对催化剂组合设计，探索乙醇催化偶合制备C4烯烃的工艺条件具有非常重要的意义和价值。

本文主要通过采用SPSS软件对乙醇转化率、催化剂、温度等数据进行相关分析，通过SPSS中的曲线估计功能找出拟合度最高的曲线，从而得出温度与乙醇转化率，以及温度与C4烯烃选择性之间的关系。然后将催化剂三种成分拆分开，即探究三种成分和温度与乙醇转化率、选择性大小的关系，四个自变量，两个因变量，又因为成分一又分为浓度和含量两个指标，因此继续拆分，转化为五个自变量，两个因变量。进而使用多重对应分析功能，分析并解决问题。

2 数据预处理

通过spss软件对现有的附件数据进行预处理，导出该数据对应的散点图，进而确定是否成线性对应关系。分析出每个变量之间对应的关系，基本确定温度与乙醇转化率、以及温度与C4烯烃选择性之间的关系，从而根据基本確定的关系设计出基础分析模型。

通过散点图可知：两者线性关系并不明显，但能明显看出随着温度的增大，乙醇转化率相应增大，进而使用SPSS软件的曲线估计功能得出较为准确的函数关系。由图2可知，其中A1，，A2，B7催化剂组合呈明显的非线性关系，在不考虑实验误差的前提下，联系化学知识可初步判断为催化剂组合对 C4烯烃选择性存在一个最适区间，当超过这一区间时，会导致选择性下降，这一发现，对于设置合适的温度来获得尽可能多的C4烯烃具有重大的意义。

3 模型建立与求解

3.1 回归模型之探究温度的影响

在每种催化剂组合下分别以乙醇转化率、C4烯烃选择性为因变量，温度为自变量，运用SPSS做出散点图（如图一），可得出变量之间的非线性关系。

建立非线性回归模型：

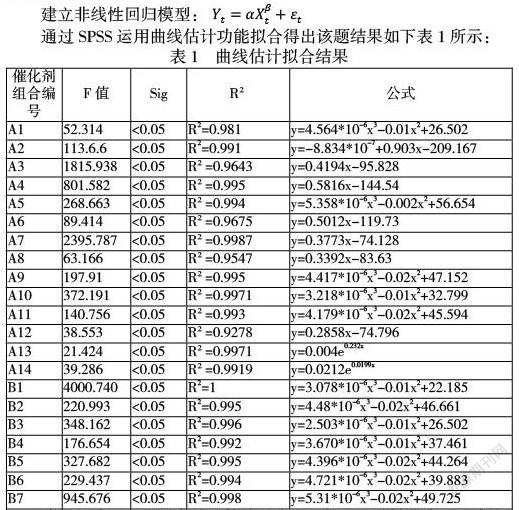
通过SPSS运用曲线估计功能拟合得出该题结果如下表1所示：

分析解读：由上图中的函数关系式即可得出乙醇转化率、C4烯烃的选择性与温度的关系，且R2均大于0.9，拟合度较高，创建的函数模型能够较好的反映乙醇转化率、C4烯烃的选择性与温度的关系。

3.2 回归模型之探究时间的影响

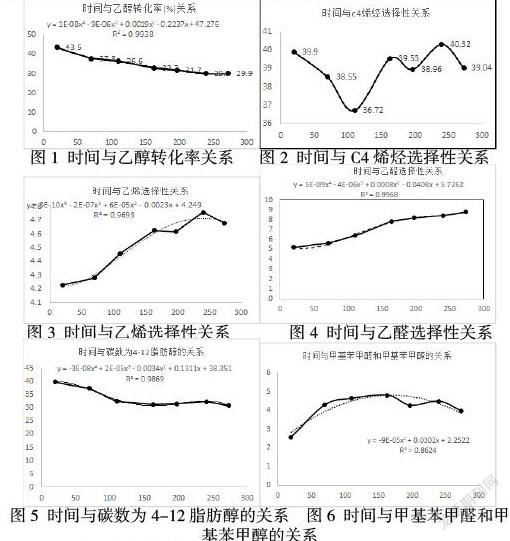
通过Excel软件制作时间与六种产物之间的关系，分别以时间为横坐标，六种产物为纵坐标，作出相应的散点图，添加趋势线拟合自变量与因变量之间的函数关系。 结果如下所示：

3.3 多重对应分析模型的建立与求解

将催化剂拆分为Co/Sio2的含量以及浓度、HAP、乙醇三部分，在工具栏中选择降维的最优标度接着在新的对话框中将“七个变量“选入分析变量的方框中，将所有变量进行联合类别图分析，得出类别点的联合图以及区分测量成分正态化图表，通过解读结果视图分析问题。视图如下：

解读方式：

1.在类别点的联合图中拟建立以（0，0）为原点的坐标轴。根据对应分析的原理，同一个变量的不同类型，如果代表它们的点散落在原点的相似方位且互相之间的距离较近，可以说明这些类别的性质相近。不同变量的不同类别，如果代表它们的散点散落在原点的相似方位且距离较近，可以说明这些类别之间具有相关关系。

2.对于区分测量图，以原点（0，0）出发的几条直线，两条线之间为锐角则具有相关关系，且距离最近的两个类别之间相关关系较大。

解读结果：

由上图可知，温度对于C4烯烃的选择性以及乙醇转化率的影响最大，催化剂对于二者的影响不及温度。此外，成分1.1——Co/SiO2的含量对于乙醇转化率以及C4烯烃的选择性影响相对于其他成分的影响较大。

4 模型评价与推广

本文采用SPSS软件对相关数据进行相关分析，建立相应的回归模型。因相应的温度与乙醇转化率、以及温度与C4烯烃选择性之间的关系未知，利用曲线估算功能找出拟合度最高的曲线，从而得出温度与乙醇转化率，以及温度与C4烯烃选择性之间的关系。该模型与回归模型结合能具有很好的解释性，并且可以通过散点图进行基础数据的分析，在模型成立的情况下对自变量和因变量进行分析，使用多重比较分析，以及相应的数据处理，进而可以迅速的得出实验的分析结果。运用降维的思想来简化列联表的结构，可以更加简单直观地呈现数据。然而该模型所呈现的多为图形，需要仔细分析，不加注意可能得到与正确结果相差甚远的结论。且难以很好地表达高度复杂的数据。

该模型能够高效、准确的对现有数据进行分析，在未来可以推广到化学实验研究的实验分析中，可以更加快捷的分析出实验中的最优解。

参考文献

[1] 勾建伟，钱耀飞，汪泽晴.分位数回归模型在高维金融数据分析中的方法和应用[J]. 知识经济，2019（5）：39-41. DOI：10.3969/j.issn.1007-3825.2019.05.024.

[2]吕绍沛. 乙醇偶合制备丁醇及C_4烯烃[D].大连理工大学，2018.

[3] Vasile Hulea.Toward Platform Chemicals from Bio-Based Ethylene： Heterogeneous Catalysts and Processes[J].ACS catalysis，2018，8（4）.3263～3279.doi：10.1021/acscatal.7b04294.

[4] 朱永杰.基于广义线性模型的混合属性数据聚类方法[J]. 科学技术与工程，2021，21（4）：1448-1453. DOI：10.3969/j.issn.1671-1815.2021.04.029.

作者简介：康佳 2000年11月 女 汉族 河南安阳 本科 学生 动物科学专业（大数据方向）