小学整数简便算法之我见

童代刚

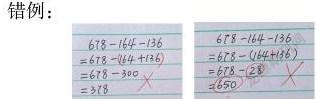
简便计算在日常生活中的应用极为广泛，在教材中也占有它独有的一席之地，在考试中它的占比约是总分的10%。其重要性不言而喻。西师版教材四年级数学上册第二单元涉及简便计算的内容，通过教学、作业和检测，我发现并总结了孩子们在简便计算方面容易出现的错误类型。现简单总结于后，希望能抛砖引玉，让大家在简便计算教学方面，能找到更适合自己教学的方式和方法。

一、与减法的性质相关的简算。

学生在运用减法的性质进行简算时，容易出现错误。正向运用“a-b-c = a-（b+c）”时，出现错误要少一些，主要错误有2个：1.忘记加小括号;2.小括号里面仍然是减号。

错例：

这种情况，说明孩子对减法的性质还没有真正弄清楚。

而逆向运用减法的性质“a-（b+c）= a-b-c”进行简算时，错误率就更高了。主要错误有2个：1.直接去掉小括号;2.忘记去小括号，直接把里面的加号改成减号。究其错误的原因，主要还是对减法的性质理解不够透彻，记得不够清楚。

错例：234-（134+87）234-（134+87）

=234-134+87=234-（134-87）

=100+87=234-47

=187=187

还有，如果出现234-（134-87）和234+（262-134）这样的和减法的性质有些相似的题目时，孩子们更是昏了头，不知道该如何做了。

为了很好的解决这类问题，我把以上含有括号的情况归结为“同级添减括号的法则”：前面是减号，添减括号要变号;前面是加号，添减括号不变号。

正解：234-（134+87）234-（134-87）

=234-134-87=234-134+87

=100-87=100+87

=13=187

234+（262-134）234-136-64

=234+262-134=234-（136+64）

=234-134+262=234-200

=362=34

234+369-269234+369+31

=234+（369-269）=234+（369+31）

=234+100=234+400

=334=634

只要是同级运算，需要去掉小括号或者需要加上小括号，都适用这个添减括号的法则。如果第一步是减法，也就是前面是减号，不管后面是添上括号还是去掉括号，后面第二步的运算符号都要改变，加就变减，减就变加。如果第一步是加法，也就是前面是加号，不管后面是添上括号还是去掉括号，后面第二步的运算符号都不变，加就加，减就减。

二、接近于整百数的简算。

接近于整百数的简便计算有四种情况：a+b（b比整百数少几），a-b（b比整百数少几），a+b（b比整百数多几），a-b（b比整百数多几）。教材上是这样说的，多加了几就减几，多减了几就加几;少加了几再加几，少减了几再减几。可是还是有不少学生把几种情况弄混淆了，分不清到底该加还是减。为了把问题简单化，我把此类问题归结为“符号法则”：比整百数少几，符号相反;比整百数多几，符号相同。

正解：345+98345-98

=345+100-2=345-100+2

=445-2=245+2

=443=247

345+102345-102

=345+100+2=345-100-2

=445+2=245-2

=447=243

前面两道题，98是接近整百数的数，它比整百数少几，那么第一步和第二步的符号相反，前面是加，后面则减;前面是减，后面则加。后面两道题，102是接近整百数的数，它比整百数多几，那么第一步和第二步的符号相同，前面是加，后面也是加;前面是减，后面也是减。这样的话，就把四种情况变成了两种情况，方便又好记，孩子们就更容易分得清楚，不易出现错误了。

三、关于同级交换的简算。

教材上没有同级交换这样的例题，也没有明确的说这类题目如何做，但是习题上有这样的题目出现，而且学生还很容易出現错误。

错例：456-87+144456-87+144

=456-144+87=456-（87+144）

=312+87=456-231

=399=225

第一种解法是只交换了数字，没有把符号也一起交换，是错误的做法。第二种做法是把它当成减法的性质来做了，关键是人家根本不是连减，怎么能减去后面两个数的和呢？

再如错例：456+188-156

=456+156-188

=612-188

=424

此题也和第一道题一样，只交换了数字，没有交换符号。这种情况，是同级运算，但是第一步和第二步的符号不同，可以交换后面两个数的位置，但是一定要记得把符号也一起交换。即同级交换法则：数字和符号一起交换。

正解：456-87+144456+188-156

=456+144-87=456-156+188

=600-87=300+188

=513=388

四、关于加法结合律的简算。

加法结合律往往同加法交换律同时使用，而且多个数相加的时候，也可以使用加法结合律。结合的原则就是凑整，能凑整的，我们就把它们结合在一起。方法是先观察几个加数的个位，个位上若能凑成整十的两个数，才有可能凑成整百。有时候是前两个数能凑整，有时候是后两个数能凑整，还有的时候是第一个数和第三个数能凑整。如果是很多个数相加，有可能能结合成多对凑整的数。

如：123+77+256287+149+151

=（123+77）+256=287+（149+151）

=200+256=287+300

=456=587

134+224+266128+145+255+72

=（134+266）+224=（128+72）+（145+255）

=400+224=200+400

=624=600

高斯巧算实际上也是运用加法结合律进行简算，他巧妙地采用首尾结合的方式，得到（1+100）+（2+99）+（3+98）+……（48+53）+（49+52）+（50+51），一共有50个101，所以1+2+3+……+98+99+100=101×50=5050。当然，按照这个思路，我们也可以用加法结合律凑整来简算：（1+99）+（2+98）+（3+97）+……（47+53）+（48+52）+（49+51）+100+50，一共有50个100和1个50，所以1+2+3+……+98+99+100=100×50+50=5050。

所以，简便计算的关键是要巧妙地用好运算律、性质和法则，通过改变运算顺序、添减括号等方式凑整，使计算变得简单。用好了简便计算，省时又省事，何乐而不为？