均匀分布Logistic 混沌序列的RRT＊路径规划算法研究

马小陆，袁书生，王兵，吴紫恒

（1.安徽工业大学 电气与信息工程学院，安徽马鞍山 243032；2.特种重载机器人安徽省重点实验室，安徽马鞍山 243032）

RRT*算法是在快速扩展随机树（Rapidlyexploring random tree,RRT）算法[1]上衍生出来的算法。RRT 算法从根节点出发，通过在规划路径的空间随机采样获取新节点并进行判断，若新节点可用，则将随机树扩展到该点，随机树通过这个方式进行扩展，最终得到一条规划的路径。但因RRT 算法使用随机方法获取新节点，树的扩展方向具有随机性，因此规划出的路径不是最优路径。针对RRT 算法的缺点，Karamen 与Frazzoli 提出了RRT*算法[2]，RRT*算法对新加入随机树的节点进行了最优路径的判断，依据判断结果确定是否对随机树重新布线，进而得到一条较优路径。由于RRT*中的概率采样算法成熟且无需对环境进行建模，因此该方法被广泛地应用在机器人的路径规划中，文献[3-4]将RRT*算法和运动学、动力学条件约束进行结合，提高了路径规划的速度和质量，并将其应用在了机器人多自由度机械臂的路径规划中；文献[5-6]对基于RRT*算法的路径规划进行了平滑处理，并将其应用在无人机的立体空间飞行轨迹规划中；文献[7]利用RRT*算法不用对空间环境建模的特点，规划出了一条粗糙的路径，再通过Dijkstra 算法对其进行了优化，并应用在无人汽车泊车场景中；文献[8]通过人工势场法优化了RRT*算法的采样过程，减少了计算量，加速了RRT*算法的收敛速度。

RRT*算法是一个渐进最优算法，若想获得较优路径，则需增加采样点，采样点的增加会使RRT*算法计算量增加，因此规划路径的时间会变长[9]。如何提高RRT*算法的收敛速度，成为RRT*算法的研究热点。Jordan 和Perez 借鉴RRT-Connect 算法双向扩展的特性，在2013 年提出了 B-RRT*算法[10]，即双向扩展RRT*；潘思宇等通过引入启发式样本代价函数，在2017 年提出了RRT*算法的改进算法[11]，提高了路径规划的速度和质量；Qureshi 等提出IBRRT*算法[12]，该算法通过加入智能采样函数加快了B-RRT*算法的收敛速度。

针对RRT*算法收敛速度慢的问题，本文提出了一种均匀Logistic 混沌序列采样的RRT*路径规划算法。该方法使用了均匀分布Logistic 混沌序列采样方法，增加了采样点的遍历性，提高了通过障碍物区域的概率，加速了随机树重布线的效率，减少了路径规划时间。

1 均匀分布Logistic 混沌序列

混沌是非线性动力学中一种特有的运动形式，混沌具有规律性、遍历性和随机性的特点。产生混沌变量的Logistic 混沌模型映射公式为：

式中：i为迭代时间步，i=0,1,···,n；xi是混沌变量，取值(0,1)；μ是混沌系统的李雅普诺夫(Lyapunov)指数，即控制参数，取值(0,4]；Logistic 映射分叉图如图1 所示。

图1 Logistic 映射分叉图

由图1 可以看出，随着控制参数μ的增加，混沌变量xi的取值从确定值增加到两倍、四倍周期分叉，最后进入到混沌状态。

文献[13]对基本Logistic 混沌序列的随机性进行了研究，当μ取(3.99,4]时，随机性较好，将μ值设定为4，x0初值设定为0.630 时，迭代40 000 次，由公式（1）得到的Logistic 混沌序列统计直方图如图2 所示。

图2 非均匀分布的Logistic 混沌序列统计直方图

由图2 可见，产生的混沌序列在（0,1）区间分布不均匀。依据文献[14]将式（1）得到的序列经式（2）处理后得到Logistic 混沌序列的统计直方图如图3 所示。

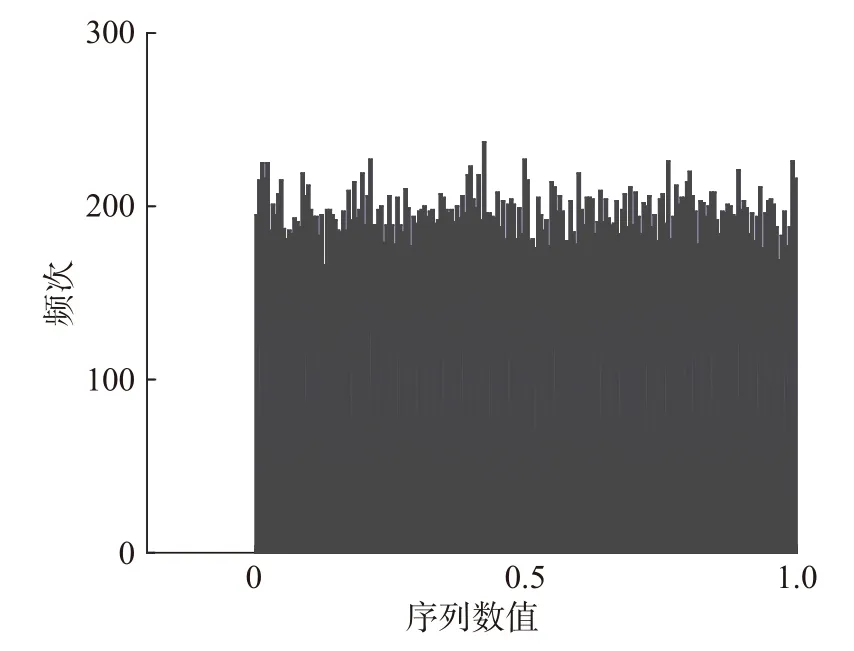
图3 均匀分布的Logistic 混沌序列统计直方图

由图3 可以看出，该序列的取值在(0,1)区间内分布均匀，此时，混沌序列的每个序列值出现的概率基本相同。

因此，本文的算法中使用式（1）和式（2）生成均匀分布Logistic 混沌序列，同时为了保证生成混沌序列的混沌性和均匀性，将生成的序列前面一些数值舍去。

2 RRT＊算法

RRT 通过状态空间的随机采样点，在空白区域内继续搜索，最终规划出到一条从起始点到目标点的路径。RRT 算法的随机树扩展模型如图4 所示。

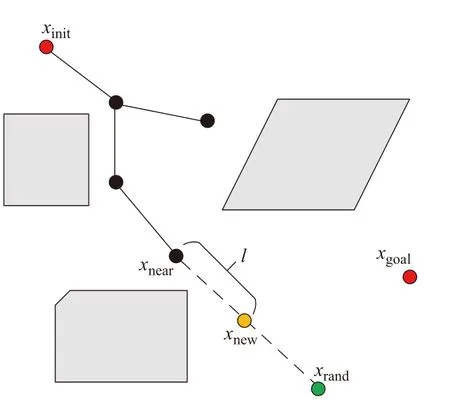
图4 RRT 算法扩展模型

图4 中，RRT 算法在规划空间里随机采样一个点xrand，然后在随机树中寻找与点xrand距离最近的点xnear，并和该点进行连线，在这条线的方向上寻找步长为l的点xnew，若点xnew可取（即不在障碍物内）且连接可行，则连接点xnew，并将其加入到随机树中。通过这样扩展的方式，能够获得一条从起点到终点的规划路径。

RRT*算法在树的扩展方式上和RRT 一样，不同之处是RRT*对xnew父节点的选取增加了重写操作，然后又对随机树进行了重新布线操作。图5 为RRT*算法父节点重写的过程。

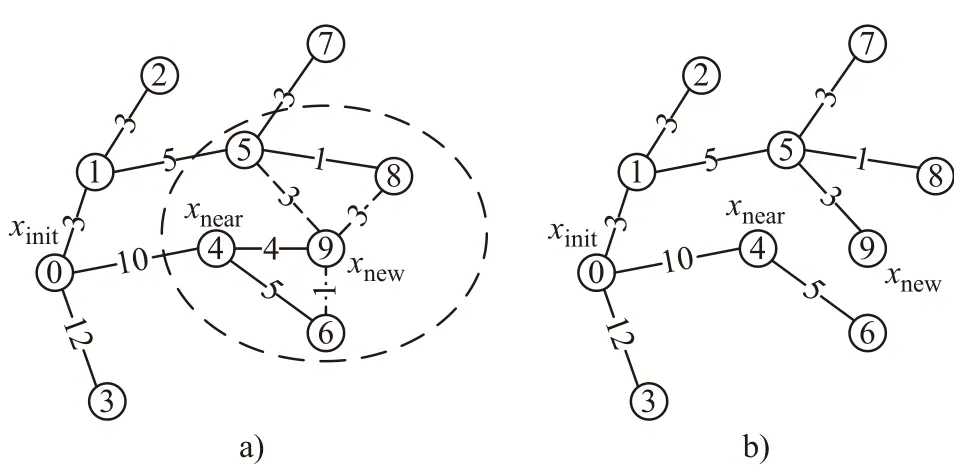
图5 RRT*算法的父节点重写

图5a）为随机树扩展过程中的某一时刻，图5a）中节点的序号大小表示节点产生的先后顺序，初始节点为0 号节点，产生的最新节点为9 号节点（xnew），与xnew节点相连接的4 号节点是xnew节点的父节点，节点和节点间连线上数字代表欧式距离即路径代价。以9 号节点为圆心，以事先规定好的半径，将xnew节点附近圈起来，图5a）中5 号、6 号和8 号节点为9 号节点的备选父节点。分别计算从起始节点经过这3 个备选父节点再到xnew节点路径的代价，并和经过原来父节点的路径代价进行比较，得到一条代价最小的路径，即将该路径的备选父节点作为xnew的父节点，再将原本的父节点断开，即可得到了图5b）所示的随机树。

重写xnew的父节点之后，再通过重新布线随机树进一步减小xnew附近的节点到起始点的代价。重新布线的操作过程如图6 所示。

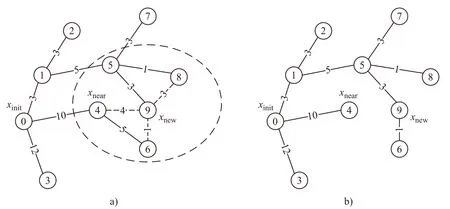
图6 RRT*算法的随机树重新布线

图6a）中9 号节点（xnew）为最新生成的节点，4 号、6 号和8 号节点为其邻近的节点，它们父节点分别为节点0、4 和5。路径分别为0→4、0→4→6、0→1→5→8，路径代价分别为10、15 和9。若将9 号节点设置为4 号节点的父节点，则路径变为0→1→5→9→4，路径代价为15，比原来的路径代价10 大，因此不对节点4 进行改写父节点操作。同理若将节点9 号节点设置为8 号节点的父节点，路径代价为14；若节点9 号节点设置为6 号节点的父节点，路径代价为12。因而对节点6 进行改写父节点操作，其随机树如图6b）所示。

可见，重新布线会让某些节点到起点间的代价变小，因此得到的路径更短。虽然最终生成的从起点到终点的路径不会包含每一个重新布线的节点，但每一次的重新布线会优化路径规划。

综上，在RRT*算法中，重选父节点会在随机树上选择一条从起始节点到最新节点间的最小代价路径，并将最新节点插入到随机树中；重布线会对随机树进行重新布局进而减少了随机树中节点到起点的冗余通路，优化重新布线路径。RRT*算法通过这两个操作来减小路径代价，但RRT*算法仍是一种渐进最优的方法，若想得到较优路径，需要增加采样点，但每增加一个采样点，需要对多个点进行父节点重写和重布线，因此，随着采样点的增加，计算量会成倍的增加，因此RRT*算法的存在收敛时间过长的问题。

3 均匀Logistic 混沌序列采样的RRT＊算法

RRT*算法在规划的空间中获取新节点方法是随机采样方法，得到的新节点具有随机性，但不能保证规划空间中样点的遍历性，特别在规划的空间中样点少的情况下更加的明显。为了解决此问题，本文提出一种基于均匀分布Logistic 混沌序列采样的RRT*算法，使得获取新节点时不仅具有随机性，还具有遍历性，该方法能提高RRT*算法的收敛速度，具体分析如下。

3.1 障碍物区域算法稳定

使用RRT*算法在进行全局路径规划时，路径在延伸扩展过程中，经常会出现路径被障碍物圈住的情况，如图7 所示。

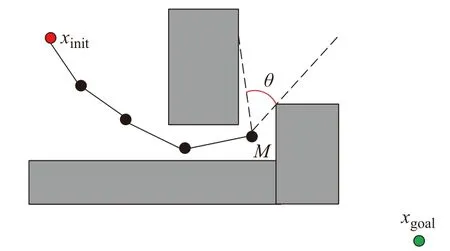
图7 RRT*算法路径扩展陷入障碍物模型

图7 中xinit为起点，xgoal为目标点，周围深色矩形表示障碍物，随机树在从起点向终点扩展的过程中，会出现如图7 所示的被障碍物围住的情况。在这种情况下，采样点只有落在图7 虚线所围成的角度范围内，才能保证随机树跳出周围障碍物并继续向后扩展。

若只考虑在角度上的采样，将图7 中M点周围以固定的角度划分为m个扇形区域，划分的模型可以简化为图8 所示。

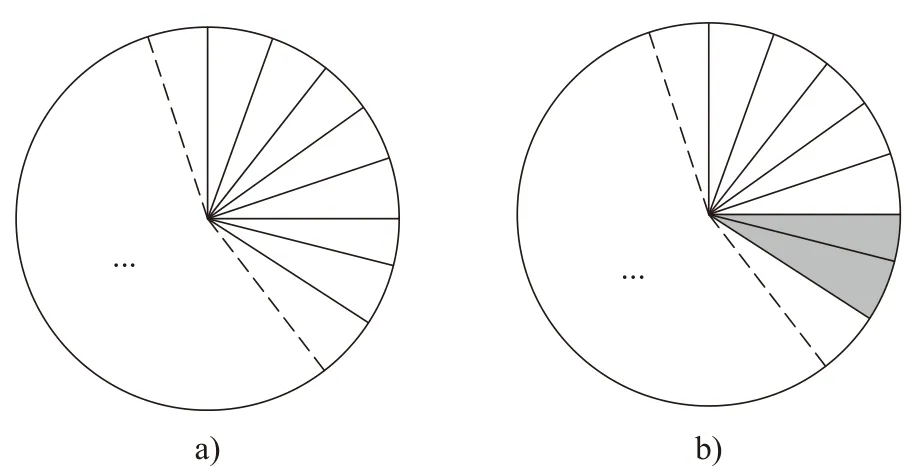
图8 两种方法角度上采样简化模型

图8a)和8b)分别表示随机数采样和均匀分布Logistic 混沌序列采样在角度上采样的简化模型，假设采样点落在每个角度范围内是等可能的，那么在第一次采样时，基于随机数采样和基于均匀分布Logistic 混沌序列采样落在图7 中θ角(即跳出被围困区域)的概率为Pθ1和此时即

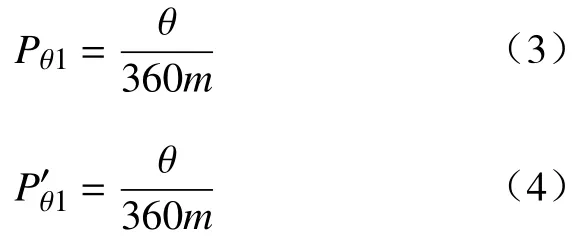
若第1 次采样时，两种方法都没有让路径扩展跳出围困区域，因基于均匀分布Logistic 混沌序列的采样的遍历会表现在角度上，若图8b)中的阴影区域表示已落在该区域的采样点，那么该区域不再考虑。因此第2 次采样时，两者的概率分别为：

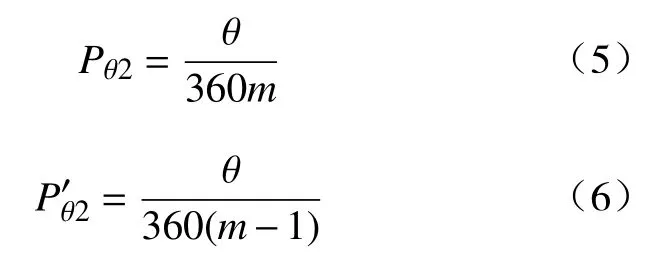
可见，Pθ2的数值依然不变，而则会变大。假设在前i-1 次的采样中，均没有跳出被围困区域，那么第i(i≤m)次采样时，基于随机数的采样概率依然不变，而基于均匀分布Logistic 混沌序列的概率为

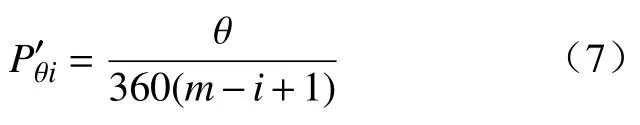
此时跳出被围困区域的概率会随着采样次数i的增加而变大。

综上可见，基于随机数采样在跳出障碍物围困区域完全基于随机性；而基于均匀分布Logistic 混沌序列采样在随机性的情况下，其遍历性会让随机的概率变大，在被障碍物围困的情况下，增加了其跳出的被围困区域的概率，加速了随机树的扩展，从而提高了算法的收敛速度。

3.2 随机树重新布线高效

图9 所示为RRT*算法规划出一条从xinit到xgoal的一条路径，图9 中各个节点虚线为重布线时考虑的半径范围，图9 中原始路径为xinit→A→B；但在采样过程中经过C点时路径的距离更短，随机树重写成xinit→C→B。对于一条除首尾节点外有n个节点的随机树，则存在n个可能重写随机树的区域。

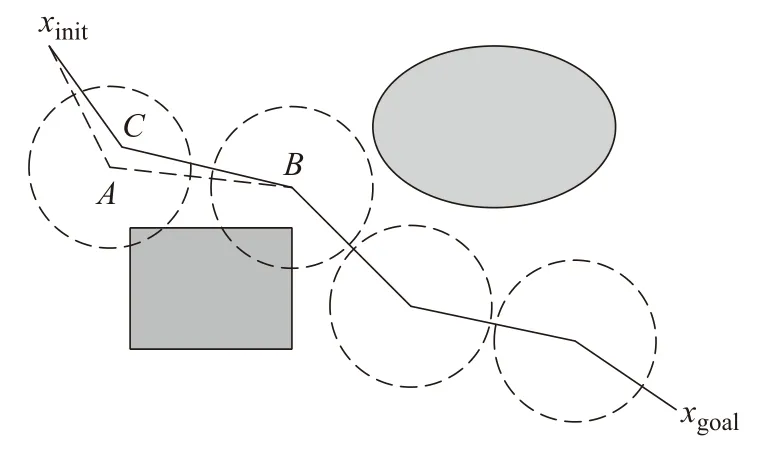
图9 随机树重新布线概率模型

图9 中，假设从左至右有4 个节点，出现可能改写区域的面积分别为S1、S2、S3、S4，整个区域内的面积为S，假设采样点占据空间大小为Ssample。则在第1 次采样的时候出现对随机树的改写的概率P1为

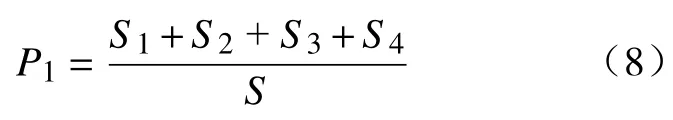
假设第1 次未对随机树进行重新布线，而在第2 次采样的时候RRT*算法对随机树的重新布线概率P2为

由式（8）和式（9）可见，随机树的重新布线概率相同。

而基于均匀分布Logistic 混沌序列采样因为除了具备随机性外还具备遍历性，在第1 次采样的时候出现对随机树的改写的概率P1同样如式（8）所示，但第2 次采样时重写随机树的概率P2会变为

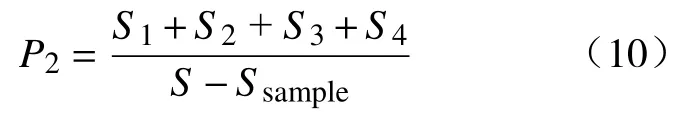
若一直都是未重新采样，则重写概率会越来越大。可见，基于均匀分布Logistic 混沌序列采样的RRT*算法对随机树的重新布线的概率除第1 次相等外，其余都比基本RRT*算法的概率要高，且这个概率随着采样次数的增加在不断增大，因此其更加合理高效，提高了路径规划的质量，从而提高了算法的收敛速度。

4 算法仿真

4.1 仿真平台

为了验证基于均匀分布Logistic 混沌序列采样的可行性，本文使用仿真对其进行验证，仿真试验地图如图10 所示。

图10 仿真试验用地图

图10 为500×500 像素的地图，图中黑色区域代表障碍物，路径规划的起点为(10,10)，终点的位置为(490,490)，在仿真试验地图上分别使用RRT*算法和基于均匀分布Logistic 混沌序列采样的RRT*算法规划路径。

4.2 仿真过程和结果分析

为方便描述，将基于均匀分布Logistic混沌序列采样的RRT*算法简称为改进的RRT*算法，分别对RRT*算法和改进的RRT*算法设置相同的采用次数，试验30 次，分别对试验规划成功的次数、路径长度及规划时间进行记录，试验采样从1 500 次开始，每次增加100 次一直到2 000 次，重复试验。通过对获取的试验数据进行统计得到的数据分别如表1～ 表5 所示。

表1 成功规划路径的平均长度 m

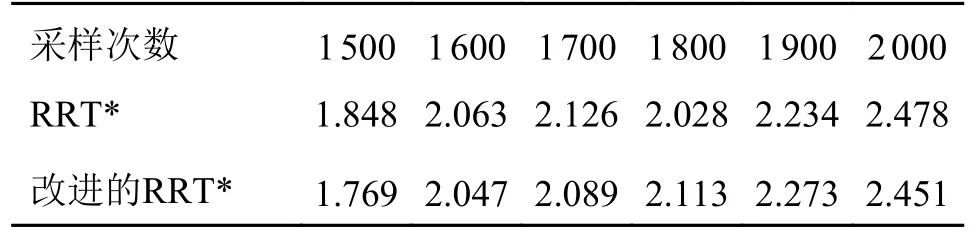
表2 成功规划路径的平均时间 s

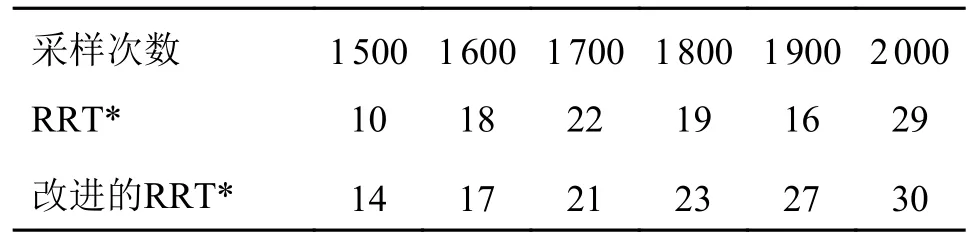
表3 成功规划路径次数

表4 成功规划路径最短路径长度 m

表5 成功规划路径最大路径长度 m

由表1 数据绘制出的成功规划路径的平均长度随采样数变化的折线图，如图11 所示。

图11 成功规划路径的平均长度变化折线图

由图11 可以看出，在采样次数相同的情况下，改进的RRT*算法规划出的平均路径长度要比基本RRT*算法规划出的路径要短。仿真结果说明了在获取相同长度的路径的情况下，改进的RRT*算法的采样次数更少，且更加稳定，因此改进的RRT*能够提前收敛。

由表2 数据绘制出的成功规划路径的平均时间随采样数变化的折线图，如图12 所示。

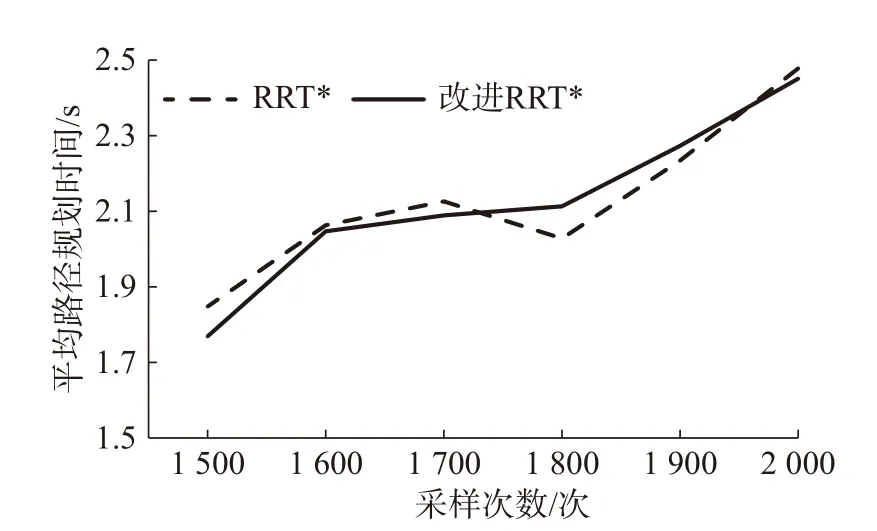
图12 成功规划路径的平均时间变化折线图

由图12 可以看出，随着采样次数的增加，两种算法消耗的时间都在增加，改进的RRT*算法和RRT*算法规划路径的时间相差不大，因而改进的RRT*算法并不会增加时间的消耗。

由表3 数据绘制出的30 次规划路径成功率的变化折线图，如图13 所示。

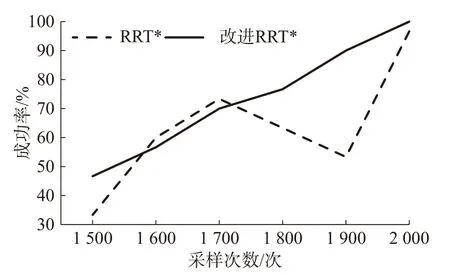
图13 规划路径成功率变化折线图

由图13 可以看出，随着采样次数的增加，改进的RRT*算法规划路径的成功率也在稳定地增加；而RRT*算法的成功率波动较大，算法不稳定。

由表4 数据绘制出的30 次规划路径成功出的最短路径长度变化折线图，如图14 所示。

图14 成功规划路径最短路径长度变化曲线图

由图14 可以看出，随着采样次数的增加，两种算法规划出的最短路径长度都在减小，但相对于RRT*来说，改进RRT*算法的最短路径稳定性更好，路径更短。

由表5 数据绘制出的30 次规划路径成功出的最长路径长度变化折线图，如图15 所示。

图15 成功规划路径最长路径长度变化曲线图

由图15 可以看出，RRT*算法规划出的最大路径长度波动较大，而改进RRT*的规划出的最大路径长度随着采样次数的增加趋于收敛，算法较为稳定。

在仿真试验中，分别对RRT*算法和改进RRT*算法分别进行一次15 万次采样的试验，耗费时间约为35 分钟，两次规划的路径长度分别为952.709 m和951.987 m，两种算法规划出的总路径长度相差不大，由于采样的次数已达到十万级别，可以将生成的路径近似当作理想的最优路径。规划出的路径基本沿着障碍物边缘，如图16 所示。

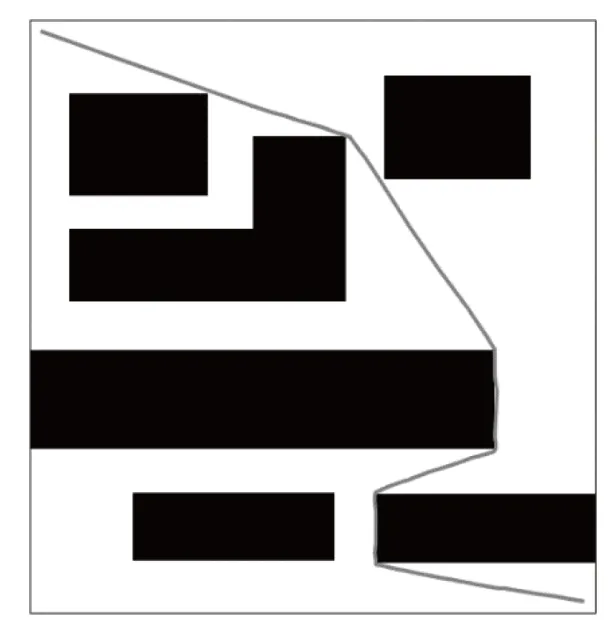
图16 理想状态的路径

图17 为多次RRT*算法规划出最长路径时的路径分布，对比图16 可以看到路径并没有从最后一个窄道通过，且在实验中发现规划出较长路径基本都存在这种情况，而改进的RRT*算法不存在这种情况。可见，基于均匀分布Logistic 混沌序列采样的RRT*算法由于采样点的合理性使得路径通过窄道的稳定性更高。

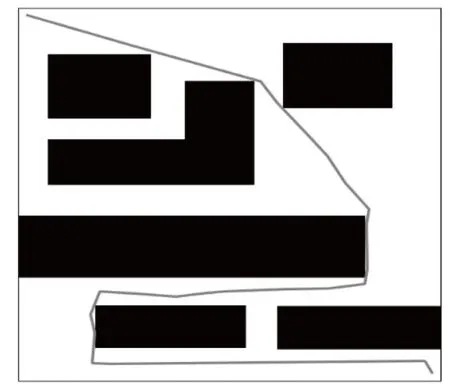
图17 RRT*算法规划出的最长路径

综上可见，基于均匀分布Logistic 混沌序列采样的RRT*算法比RRT*算法需要更少的采样点且算法稳定。

5 试验验证

5.1 试验平台

试验平台为实际应用的移动机器人底盘，其系统架构如图18 所示。

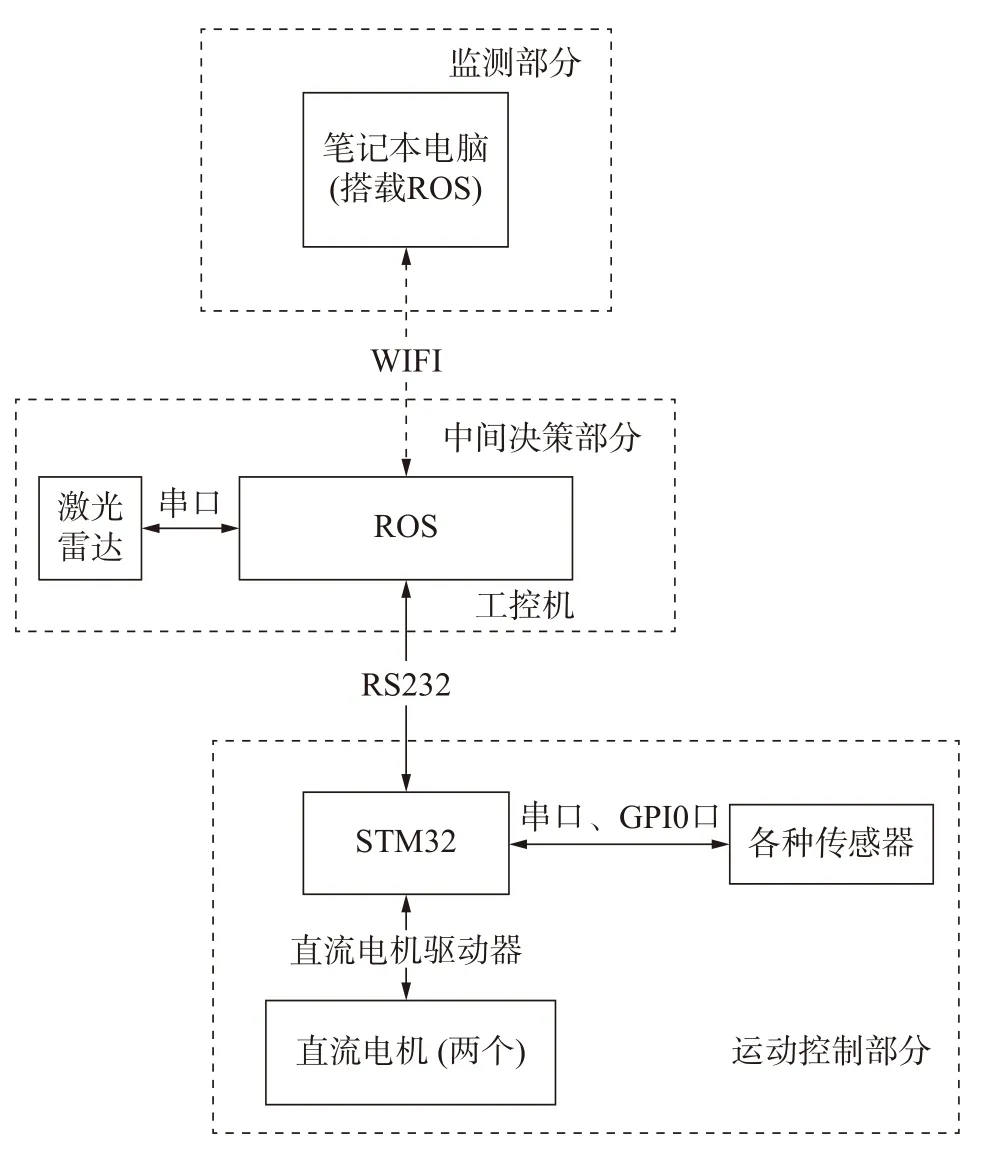
图18 移动机器人底盘系统架构图

由图18 可以看出，系统主要分为3 个部分：底盘运动控制部分、中间决策部分、监测部分(上层命令下发等)。底盘运动控制部分，主要采用STM32单片机来处理来自决策部分的控制命令，主要有机器人速度的控制，编码器、IMU 等各种传感器数据的采集以及上传，底盘运动控制部分和中间层通过RS232 来进行数据的交换。中间决策部分是一块搭载了Ubuntu16.04 的x86 工控机。在该系统上已搭建好ROS 环境，主要负责机器人的实时定位、路径规划等运算量比较大的部分。上层监测部分使用的是一台已经搭建好ROS 环境的笔记本电脑，该电脑通过无线网络接入系统，这样可通过远程的方式对决策部分下发命令，同时可以实时监控导航的效果。移动机器人的底盘的外部和内部实物图分别如图19 和图20 所示。

图19 机器人底盘实物外部

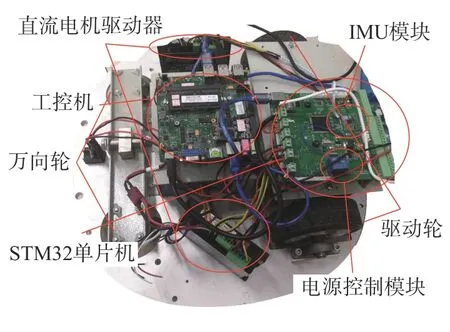
图20 底盘实物图内部

5.2 试验方法和试验结果

试验的场地为所在的实验室，其扫描出的地图如图21 所示。

图21 试验用地图

不像A*算法那一类的最优算法，能够找到一条最优路径。RRT*算法和改进 RRT*都是于基于概率采样得到的路径，属于渐进最优的算法，尽管随着采样次数的不断增多能够无限趋近于最优路径，但是获得的路径与所付出的计算资源完全不成正比。因而在使用这类算法时，只需得到一条相对较优的路径的前提下占用的资源较少即可。

在应用改进RRT*算法和RRT*算法时，规划出来的路径相对其它算法来说随机性较高，无法确保实验的重复性，即无法保证两次规划出的路径重合。并且在试验场景相对简单的情况下，仿真试验中性能对比的结果并不是特别明显。所以在实际的机器人上试验时，使用了大多数路径规划性能比对的方案，即以规划出的路径长度和规划的时间来衡量算法的性能。为了排除采样算法的偶然性，试验方案选取同一个起点和同一终点间进行多次（30 次）的路径规划，对规划出的时间，路径长度以及采样点数量进行了统计，然后取均值进行比较。

图22 所示为试验中选取两点规划出比较好的路径截图，图22a）、图22b）中起点、目标点1 和目标点2 用椭圆标出，从起点到目标点1 和目标点2 之间的线条即为规划出的路径。

图22 路径规划试验结果图

当以目标点1 作为终点时，RRT*算法和改进的RRT*算法路径规划数据（30 次试验的平均数据）如表6 所示。

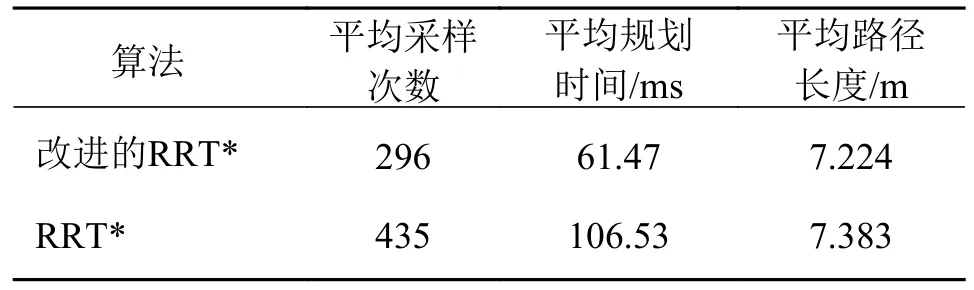
表6 目标点1 下两种算法性能比较

由表6 可以看出，当以目标点1 为终点时，RRT*算法采样点个数为435，而改进RRT*算法采样点个数为296，采样点数减少了31.95%，因采样点数有所减少，路径规划时间减少了42.29%，路径长度减少了2.2%。

当以目标点2 作为终点时，RRT*算法和改进的RRT*算法路径规划数据（30 次试验的平均数据）如表7 所示。

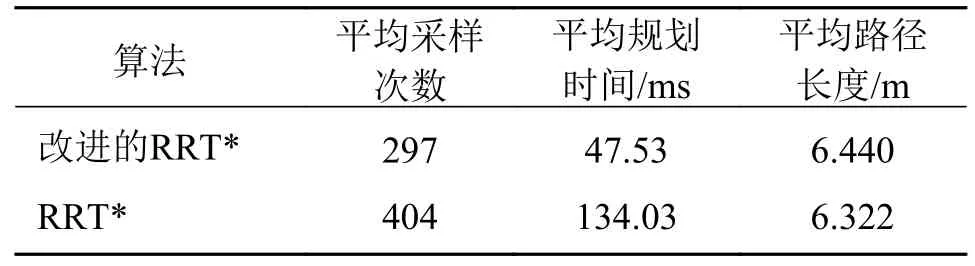
表7 目标点2 下两种算法性能比较

由表7 可以看出，当以目标点2 为终点时，RRT*算法采样点个数为404，而改进RRT*算法采样点个数为297，采样点数减少了26.49%，路径规划时间减少了64.52%，路径长度增加了1.9%。

试验结果表明，改进的RRT*算法能够加快路径向最优路径的收敛速度。在规划出相同长度路径的情况下，改进的RRT*算法所需要的采样点数更少，规划出路径的时间更短。即在采样点相同的情况下，改进的RRT*算法能够获得更短的路径。

6 结论

本文提出了一种基于均匀分布Logistic 混沌序列采样的RRT*路径规划算法，该方法通过采用Logistic混沌方法代替随机数方法生成RRT*算法采样点，不仅保证了采样点的随机性，也增加了采样点遍历性，使得采样点在分布上更具合理性和有效，提高了通过障碍物区域的概率，加速了随机树重布线的效率，加速了RRT*算法的收敛速度。通过仿真和实验验证均表明基于均匀分布Logistic 混沌序列采样的RRT*算法能够提高路径规划的收敛速度。相对传统的RRT*算法，在相同的路径长度，改进的RRT*算法所需要的采样点数更少，规划路径的时间更短，稳定性更高。