偏置式空间RSSR 急回仿生扑翼机构优化设计与分析

张瑞坤，何畏*,，王习术，郑家伟，孙磊

（1.西南石油大学 机电工程学院，成都 610500；；2.清华大学 航天航空学院，北京 100083；3.宝石机械成都装备制造分公司，成都 610052）

近年来，随着空气动力学、仿生学、微机电系统制造等技术的飞速发展，微型飞行器（Micro air vehicle,MAV）进入了人们的视野。根据飞行升力产生方式的不同，微型飞行器分为：旋翼型、固定翼型和扑翼型3 种[1]。其中扑翼飞行器（Flapping-wing MAV）是一种模仿生物飞行机理，利用侧翼上下扑动产生升力和推力来实现飞行的新型飞行器。与旋翼型和固定翼飞行器相比，扑翼飞行器具有飞行灵活、耗能少的特点，因而更受到研究者的青睐，也成为当前研究的热点[2]。

根据扑翼机构不同，目前的研究主要可以分为模仿昆虫的多自由度扑翼机构和模仿鸟类的单自由度扑翼机构[3]。其中多自由度扑翼机构多采用多个驱动机构进行分路驱动或者使用一个复杂的机构同时实现多个运动[4]，机构复杂，不适合应用于微小型扑翼飞行器。目前，研究较多的单自由度扑翼机构大都基于平面连杆机构进行改进设计，常见的单自由度驱动机构有单曲柄双摇杆驱动机构、曲柄滑块驱动机构、双曲柄双摇杆驱动机构、凸轮弹簧驱动机构等[5-7]。而对于空间连杆机构在扑翼飞行器的应用研究较少。另外研究发现鸟类在扑翼飞行时，翅翼上下扑动所占的时间比值也不相同，通常翅翼下扑所占时间约占整个扑动过程的60%～80%[8]，这样有利于增大下扑时产生的升力，减小扑翼上扑时产生的阻力。而目前的单自由度扑动机构大都没有考虑到扑翼运动的急回特性。

因此，本文在对平面曲柄摇杆扑翼机构分析的基础上，结合了空间连杆机构结构紧凑、灵活可靠的特点[9]，设计一种基于偏置式空间RSSR 机构的扑翼机构。通过电机匀速驱动即可实现扑翼急回扑动，通过对其运动学建模及优化设计，设计出简单有效且符合鸟类扑动规律的扑翼机构。

1 扑翼机构分析

单自由度扑翼机构主要是实现扑翼飞行器侧翼的上下扑动，其中最先提出的是如图1 所示的单曲柄双摇杆机构，曲柄OA在电机带动下绕O做圆周运动，通过连杆AB1、AB2带动双摇杆B1O1、B2O2绕O1、O2上下扑动。这样该扑动机构可以将电机的连续转动转化成扑翼的往复上下扑动。但是这种机构在运动时，由于机构非对称性导致左右两侧翼非同步运动，从而导致扑翼飞行器发生栽落[10]。为了提高扑翼飞行器翅翼扑动的对称性人们采用提前分离运动支链的方法得到了如图2a）所示的双曲柄双摇杆机构，同步运动的两个曲柄O1A1、O2A2通过连杆带动左右两个摇杆B1C1、B2C2同步扑动，但是由于引入了齿轮副，传动效率会有所损失[11]；图2b）所示的曲柄滑块机构，滑块B沿着中间滑槽滑动，带动左右两个摇杆同步上下扑动，但由于使用了滑动副，大大降低了机构的传动效率。采用改进机构构形得到如图3 所示的含球副的空间扑翼机构，电机带动两个曲柄同步转动，曲柄通过连杆带动左右两个摇杆绕同步上下扑动[12-13]。

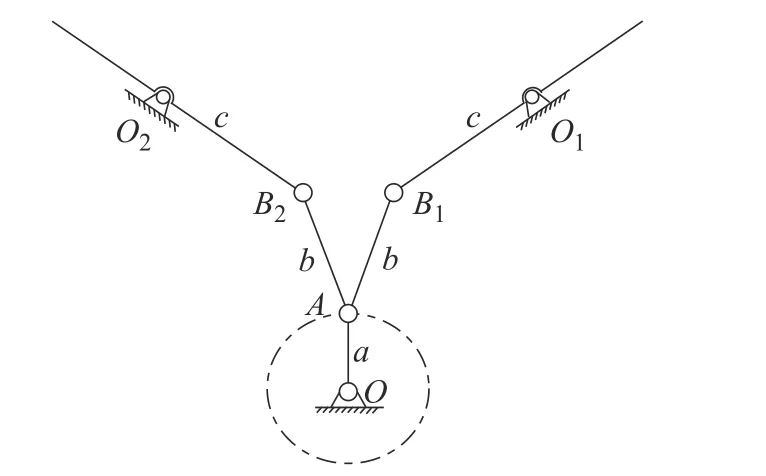
图1 单曲柄双摇杆机构简图

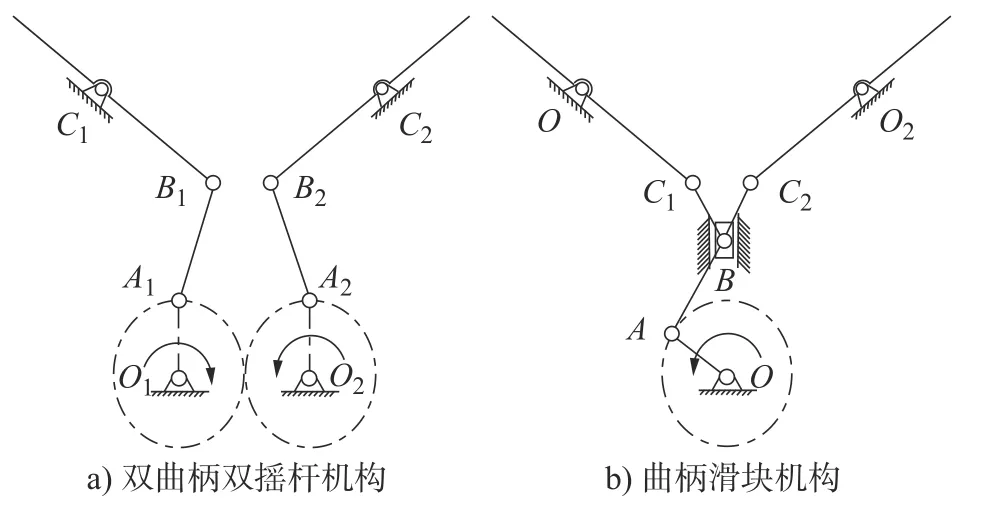
图2 分离运动支链的平面扑翼机构

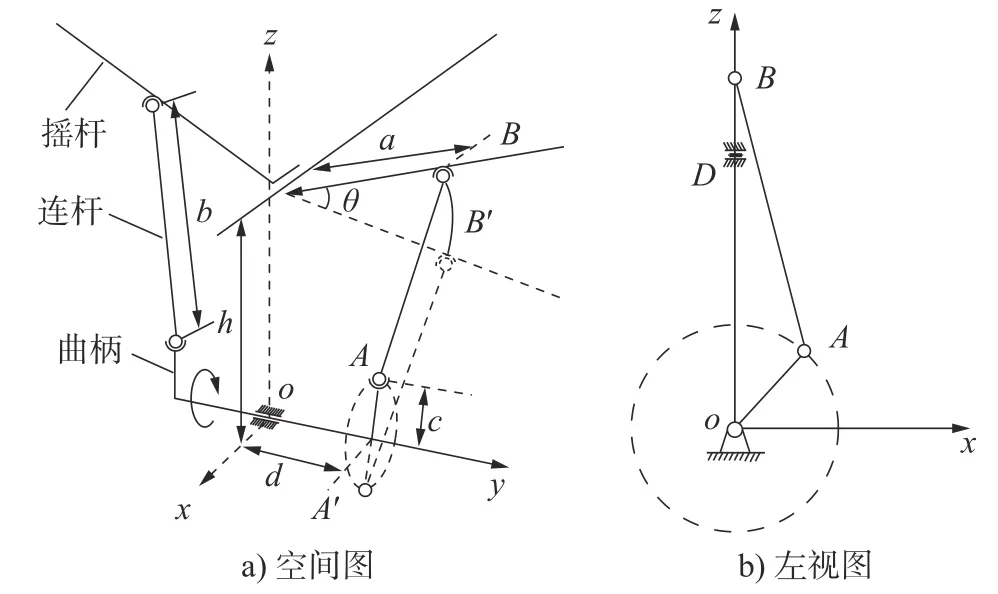
图3 改进机构构型的空间扑翼机构

图3 所示的空间曲柄机构很好解决了两摇杆的运动因存在相位差问题，但是由机构的对称性可以看出左右两个摇杆在扑动过程中扑动角度的上下行程用时一样，即机构属于无急回特性机构，而鸟在飞行过程中。为了保证翅翼扑动时具有良好的气动特性，要求下扑行程占据整个行程的60%左右[8]，即具有急回特性。故本文在图3 基础上对曲柄进行偏置处理，提出如图4 所示的偏置的空间曲柄摇杆机构作为扑翼飞行器的扑动机构。

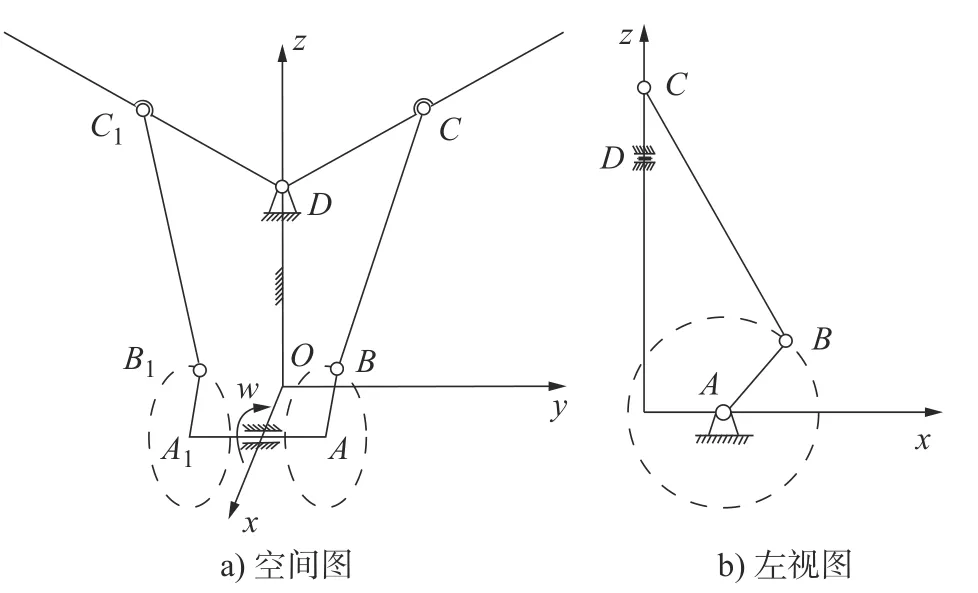
图4 偏置的空间RSSR 曲柄机构

图4 所示偏置式空间RSSR 扑翼机构工作原理为：曲柄AB、A1B1在电机驱动下同步转动，通过连杆BC、B1C1带动CD、C1D两摇杆绕机座D点同步上下扑动。

2 扑动机构运动学分析

两个RSSR 机构关于竖直平面对称，为方便研究，以右扑翼作为研究对象。以曲柄O为坐标原点，飞行器前行方向OE为x轴，机架OD为z轴建立图5 所示的空间直角坐标系。其中曲柄AB长度为l1、连杆BC长度为l2、摇杆CD长度为l3、机架OD长度为l4、曲柄偏置距离OE为e、曲柄水平距离AE为L、曲柄转动角度为θ、摇杆扑动角度为φ。

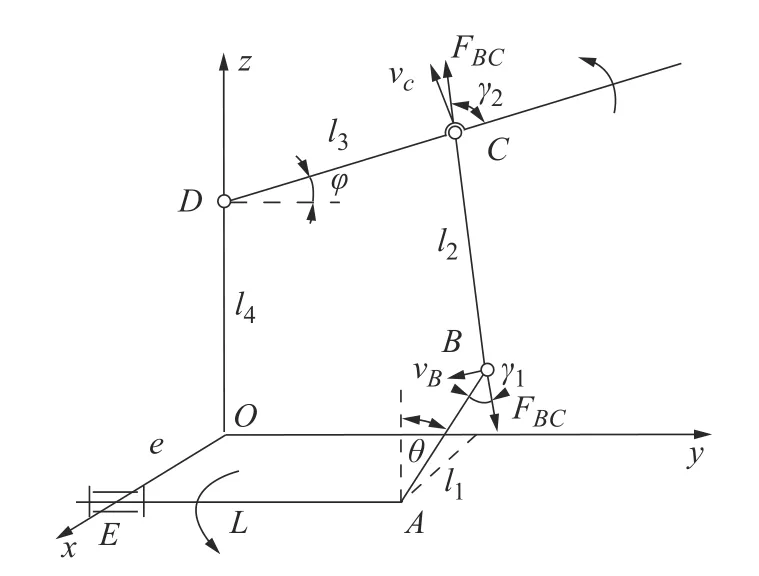
图5 机构坐标系及杆长定义

根据图5 建立的空间直角坐标系可以得到各点坐标分别为：A(e,L,0)，B(e+l1sinθ,L,l1cosθ)，C(0,l3cosφ,l4+l3sinφ)，D(0,0,l4)。

采用拆杆拆副法，建立输入角θ与输出角 φ的关系式，得到连杆l2的约束方程为

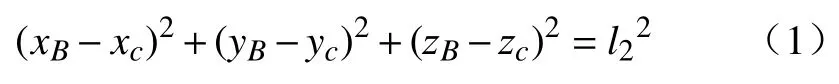
将B、C两点坐标代入连杆l2的约束方程得到空间曲柄摇杆机构的角位移求解方程，即

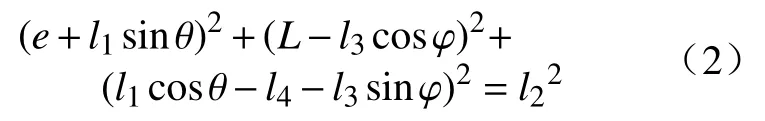
将式（2）展开并整理得到摇杆扑动角度φ 曲柄转动角度θ 的关系为

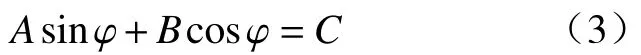
式中：A、B、C分别为：

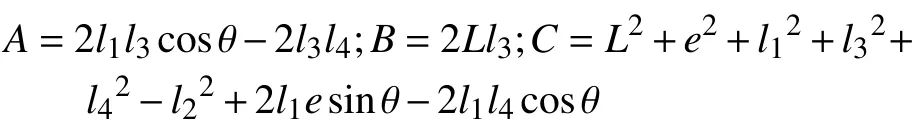
运用三角函数万能公式得到：

把式（4）代入式（3）得到摇杆扑动角度的计算公式为

由式（5）可得，摇杆扑动角度 φ除了与曲柄输入角θ、l1、l2、l3、l4、e、L有关。若直接根据式（5）进行设计，则由于设计的参数较多且未将机构的结构条件、力学性能以及扑翼机构的扑动要求等考虑进去，造成计算过程较为复杂、机构载荷传递效果不好且摇杆扑动达不到扑翼飞行器侧翼扑动要求等问题。故需要对偏置式空间RSSR 机构进行优化设计。

3 扑翼机构的优化设计

3.1 设计参数的选取

单选取空间摇杆机构的3 个杆长l1、l2、l3、机架OD长度为l4、曲柄偏置距离OE为e、曲柄水平距离L作为扑翼飞行器扑动机构的优化综合设计的尺寸参数。因机构整体尺寸的放大或缩小不对扑翼机构摇杆的角运动关系产生影响，故采用无量纲相对杆长对各尺寸参数进行处理。以曲柄长度l1为参考，r1=l1/l1=1，连杆BC杆长r2=l2/l1，摇杆CD杆长r3=l3/l1，机架OD长度r4=l4/l1，偏置距离OE为r5=e/l1，曲柄水平距离AE为r6=L/l1。则优化设计变量X=[x1,x2,x3,x4,x5]=[r2,r3,r4,r5,r6]。

3.2 约束条件

1）为了保证机构具有良好的传力性能，应使最小传动角大于 40°，即最大压力角不能大于50°[14]。

（1）曲柄AB与连杆BC之间最小传动角应大于等于 40°，即

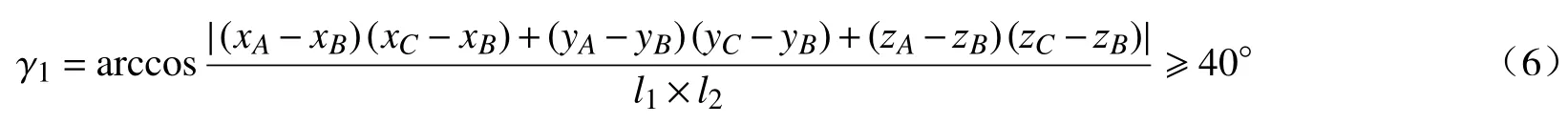
（2）摇杆CD与连杆BC之间最小传动角不小于40°，即

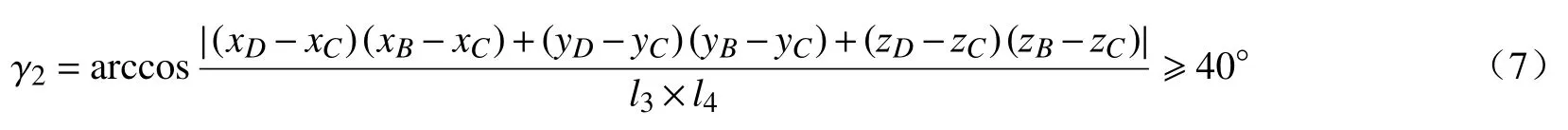
2）由于该机构在B、C两处使用了球面副，在实际生产条件下，一般使用关节轴承。查阅目前大规模生产的关节轴承型号，发现其中的杆端关节轴承的摆角“一般不大于 30°”。因此球面副上的两个构件运动角度范围必须在 60°之内才能满足关节轴承的要求[15]。

（1）曲柄AB与连杆BC夹角 ϕ1的最大值与最小值差小于等于 60°，即

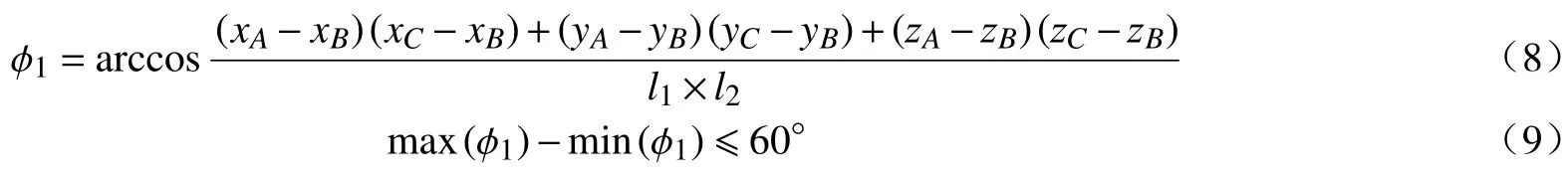
（2）摇杆CD与连杆BC夹角 ϕ1的最大值与最小值差不大于 60°，即

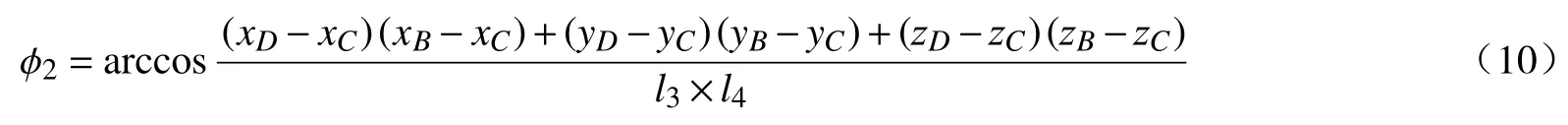
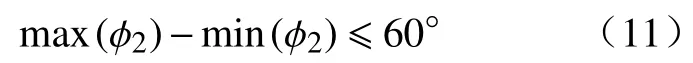
3）摇杆扑动角度φ 计算方程有解，则

3.3 目标函数

为了使扑翼飞行器在扑动飞行时产生足够的升力和推力，根据仿生学原理，扑翼飞行器扑动机构摇杆的运动规律应尽量与鸟类飞行翅翼运动规律相同。根据文献[12]，中型鸟类扑动幅度为 40°，上极限位置为 22°，下极限位置为-18°。故空间曲柄摇杆扑动机构的摇杆扑动角度 φ应尽量与鸟类飞行翅翼扑动角度相同。得到目标函数为：

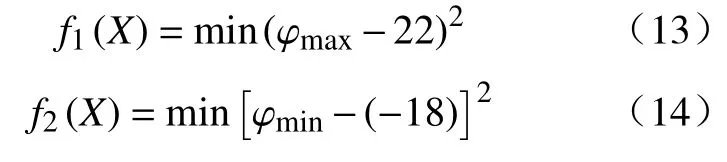
根据文献[8]发现鸟类的扑翼运动中，上下扑动所占的时间比值是不相同，通常向下扑动时间大约占整个扑动过程的60%左右，这样有利于增大下扑时产生的升力，减小向上扑动时产生的阻力。这就要求摇杆在运动过程中具有急回特性。为了表明翅翼上下往复扑动的急回程度，选用行程速比系数K0来衡量，即

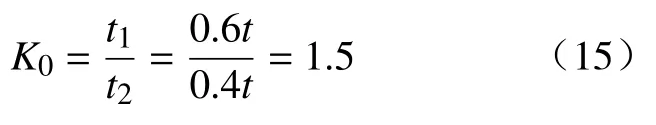
式中：t1为一个周期内下扑时间；t2为一个周期内上扑时间；t为扑动一个周期的时间。

为了使扑翼飞行器能够像鸟类飞行时一样具有良好的气动特性，扑翼飞行器的偏置式空间RSSR扑动机构的行程速比系数尽量接近鸟类的行程速比系数。得到目标函数为

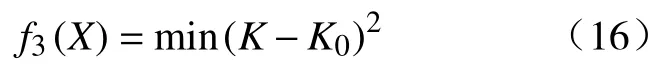
根据目标函数的选取，可知扑翼机构设计属于多目标函数优化问题。为方便求解，给每个子目标函数赋予权重，通过线性加权得到综合评价函数。

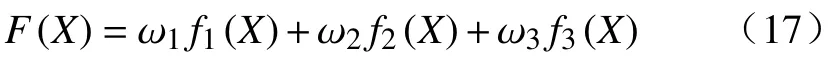
式中：ω1、ω2、ω3分别为各子目标函数的权重，且ω1+ω1+ω3=1，根据各个参数对扑翼飞行器升力、推力的影响程度，选取ω1=0.3，ω2=0.3，ω3=0.4，则该多目标优化问题就转化为单目标优化问题。

3.4 优化求解

根据上文建立的优化模型，利用MATLAB 采取遗传算法和调用非线性规划函数fmincon 对扑翼飞行器的扑动机构的相对尺寸参数进行优化，算法流程图如图6 所示。

图6 非线性规划遗传算法流程图

其中优化参数初值以及其变化范围如表1 所示。

表1 优化参数初值及范围

通过计算，最终得到优化结果为

优化前后两个周期的摇杆输出角度如图7 所示，扑动上极限夹角由20.26°变成22.00°，下极限夹角由-14.13°变成-18.00°，扑动角度达到了理想值。

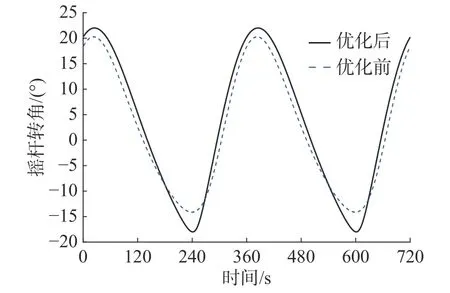
图7 优化前后摇杆输出角对比

4 设计案例分析

4.1 优化设计计算

设计实例依照鸟的飞行姿态进行仿生设计，飞行器机身长度约800 mm，宽度约120 mm，整个翼展为1 m[11]。为保证扑翼飞行器机身宽度设计满足要求，选取曲柄长度为10 mm，根据优化得到相对杆长关系计算得到l1、l2、l3、l4、e、L尺寸如表2 所示。

表2 扑翼机构尺寸参数 mm

将l1、l2、l3、l4、e、L值代入式（5）得到扑翼飞行器两个周期内扑动机构摇杆扑动角度 φ随曲柄驱动角θ 变化曲线如图8 所示。

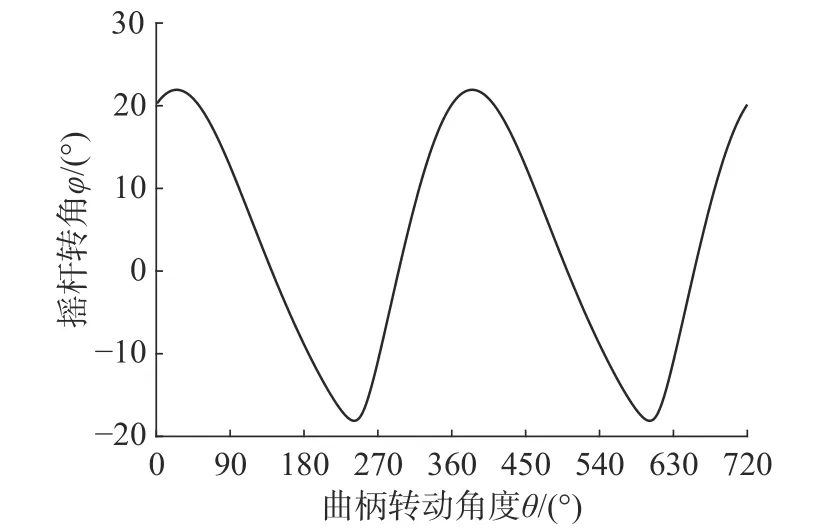
图8 扑翼扑动角度φ随驱动角θ 变化曲线

由图8 可知，曲柄在转动一周内摇杆扑动上极限夹角φmax=21.92°，对应曲柄转角为 25°；下极限夹角φmin=-18.11°，对应曲柄转角为241°；则对应摇杆摆角为

极位夹角为

行程速比系数为

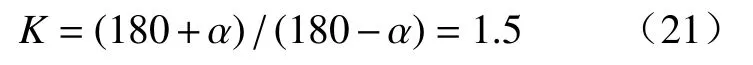
摇杆扑动角度与行程速比系数与目标函数要求相符合，该偏置式空间RSSR 扑翼机构能达当扑翼飞行器扑翼机构设计要求。

将l1、l2、l3、l4、e、L尺寸值代入式（6）、式（7），利用MATLAB 求解并绘制曲柄转动一个周期内曲柄与连杆，连杆与摇杆在球副B，C处的传动角曲线图，如图9 所示。

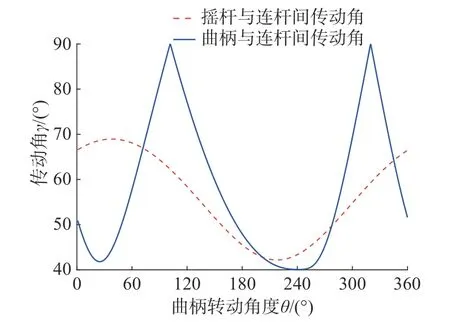
图9 扑翼机构相关杆件传动角变化曲线

由图9 可知，曲柄AB与连杆BC间的最小传动角γ1min=42.18°；摇杆CD与连杆BC间的最小传动角为γ2min=40.01°。故在B、C两处传动角均大于40°，满足机构传力要求。

将l1、l2、l3、l4、e、L值代入式（8）～式（12），利用MATLAB 求解并绘制曲柄转动一个周期内曲柄与连杆在球副B、连杆与摇杆在球副C处相连两构件夹角变化曲线图，如图10 所示。

图10 扑翼机构相关杆件间夹角变化曲线

由图10 可知，在曲柄运动一个周期内，曲柄AB与连杆BC间的最大夹角为117.64°，最小夹角为57.64°，夹角变化为60.00°；摇杆CD与连杆BC间的最大夹角为137.82°最小夹角为111.05°，夹角变化为26.77°。故在B、C两球副处两个构件运动角度变化范围均不大于 60°，满足关节轴承的结构要求。

4.2 驱动机构模型仿真验证

为验证驱动机构理论的合理性，根据扑翼机构的优化结果，建立RSSR 机构的仿真模型，在 ADAMS/View 中输入各点初始坐标。然后进入圆柱体建模连接对应点坐标。建立好模型后需添加适当的运动副。根据 RSSR 机构运动副特点在曲柄与连杆、连杆与摇杆两处建立球副，在曲柄与机架、摇杆与机架连接两处建立转动副。根据参考文献[3]，取扑动频率为5 Hz，在曲柄处添加驱动，给定驱动速度为300 r/min。ADAMS 仿真模型如图11 所示。

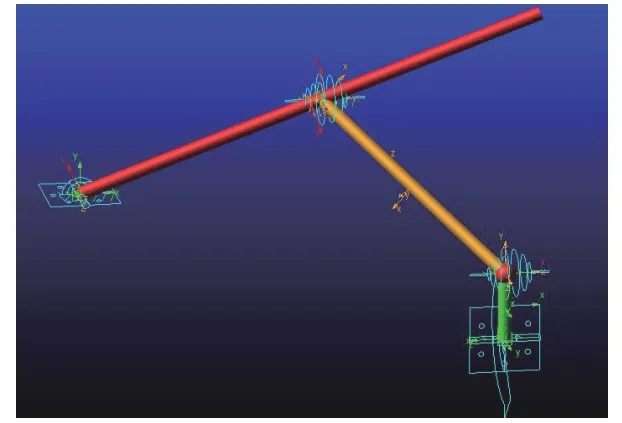
图11 ADAMS 仿真模型

进行运动仿真后，通过建立参考点，测量摇杆输出角度。在 ADAMS-PostPro-cessor 中查看测量曲线，并与理论计算值进行比较，得到两个周期内的扑翼运动曲线如图12 所示。结果显示ADAMS 仿真得到的摇杆输出角度曲线与机构学理论计算与结果一致，证明理论分析的正确性。

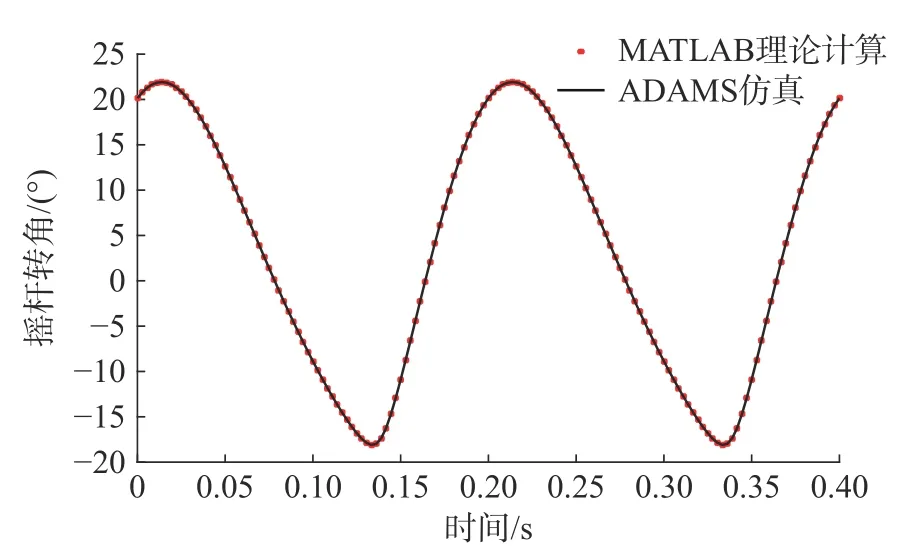
图12 理论计算与ADAMS 仿真输出对比

5 结论

1）扑翼机构在扑动过程中，机构最小传动角γmin=40.01°，两个球副处，相连杆件间夹角最大变化为 60°，具有较好的传力性能。

2）扑翼机构行程速比系数为1.5，极限夹角φmax=21.92°，下极限夹角φmin=-18.11°，与选取鸟类飞行参数一致，具有良好气动性能。

3）利用ADAMS 对优化后的机扑翼机构进行仿真分析，得到摇杆扑动角度ADAMS 仿真分析曲线和MATLAB 理论计算分析曲线一致，验证了理论分析的正确性。