改进型自抗扰解耦的PMSM 调速控制方法研究

付文强，赵东标，张瑶

（南京航空航天大学 机电学院，南京 210016）

永磁同步电机（PMSM）在航空工业领域得到广泛的应用[1-3]。对其采用矢量控制方法进行速度控制时，就必须解决电流环耦合性问题[4]。国内外研究学针对永磁同步电机调速控制提出了很多先进的控制方法，如滑模控制[5]、鲁棒控制[6]、自抗扰控制[7]等。

永磁同步电机是强耦合、非线性系统。为了提高其控制性能，学者提出了前馈解耦控制、内膜控制等[8-9]，但是大部分解耦方法对系统的模型或是系统的参数具有很强的依赖性。

自抗扰控制不依赖于准确的模型，可很好的解决多变量系统的耦合性问题[10-11]。自抗扰控制一般由跟踪微分器、状态误差反馈控制率、扩张状态观测器、扰动补偿构成。跟踪微分器主要是安排过渡过程；扩张状态观测器可以对负载及参数扰动进行观测；状态误差反馈控制率对误差进行调节；最后进行扰动补偿[12]。自抗扰控制器具有较强的适应性和优良的控制性能，为了便于控制，减少被控参数的个数，采用线性函数来取代非线性函数，即线性自抗扰控制器（Linear active disturbance rejection controller,LADRC）[13-14]。

本文考虑电流环参数变化及各种非线性扰动因素，引入“虚拟控制量”设计了一种改进型的线性自抗扰解耦控制器，实现了对电流环的解耦控制。速度环采用线性自抗扰控制器，对负载扰动进行观测和补偿，提高系统的抗扰动能力。仿真试验表明，该控制策略提高了电流环的解耦性能，增强了系统的鲁棒性，系统的调速性能及抗干扰能力有了很大的提升。

1 PMSM 数学模型推导

研究PMSM，通常需要建立以下几个假设：1）忽略铁芯的饱和影响；2）电机中的电流为三相正弦波电流；3）不考虑电机的磁滞和涡流损耗[15-16]。

综合考虑扰动影响，d-q轴系中表贴式PMSM的数学模型如下：

式中：id,iq均为定子绕组在同步旋转坐标系下的电流分量；ud,uq均为定子绕组在同步旋转坐标系下的电压分量；Rs和Lq=Ld=L分别为定子的电阻和电感；ωm为转子的机械角速度；ψr为转子永磁磁链；np为极对数；J和B分别为转动惯量和阻尼系数；TL为负载转矩；fd和fq均为检测误差和采样延时以及参数变化等各种非线性因素带来的扰动。

从式（1）可以看出，PMSM 控制系统存在内部扰动以及外部负载等综合扰动的影响。

2 改进型自抗扰解耦电流环控制

2.1 解耦控制策略设计

由式（1）电流电压方程整理可得：

通过自抗扰控制技术对其进行解耦设计，变量为：

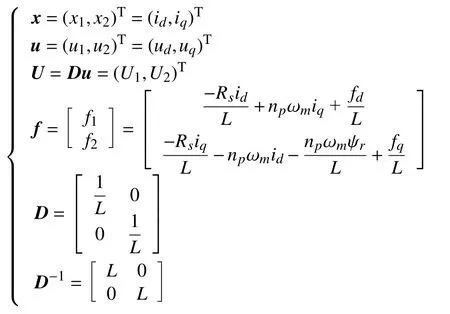
式中：D为可逆矩阵；f可视为系统的“动态耦合”部分；U可视为系统的“静态耦合”部分。根据自抗扰解耦理论，若D为可逆矩阵，则系统可以进行解耦。则式（2）可以简化为：

从式（3）可知，系统的输出y与U构成了单输入单输出的关系，将U称之为“虚拟控制量”。输出的实际电流id,iq分别只与虚拟控制量U1,U2有关，表明系统电流环通过虚拟控制量实现了完全解耦。

将f视为系统的总扰动，根据自抗扰理论，可以在控制器输出Ui和控制器输入xi之间嵌入一个自抗扰控制器，实现对输入的跟踪解耦。整个解耦过程如图1 所示。

图1 自抗扰解耦过程图

根据图1 可知，采用自抗扰解耦技术进行解耦时，不需要考虑“动态耦合”部分。“动态耦合”可以通过观测器进行观测和补偿，不依赖于系统的准确参数。极大的提高了解耦性能和可操作性。

2.2 改进型自抗扰电流环解耦控制器设计

若直接对总扰动f进行观测，由于扰动幅值较大，会使得扰动观测精度受到影响。根据式（2）可知，f可视为由两部分组成，整理可得：

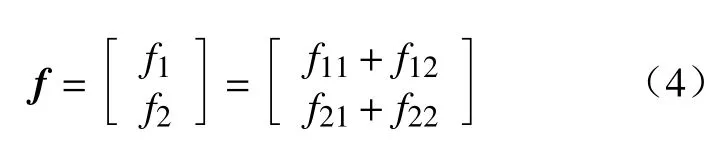
式中：f11和f21视为系统的已知扰动，可以计算得出，f12,f22是各种因素综合的未知扰动，利用观测器进行观测，f12=fd/L，f22=fq/L。若将已知扰动直接嵌入自抗扰控制器中，可以极大的减轻观测器的负担，提高扰动观测精度，进而提高控制器的性能。

以q轴电流环控制器为例进行设计，具体如下：

1）线性跟踪微分器设计。

2）线性扩张状态观测器设计。

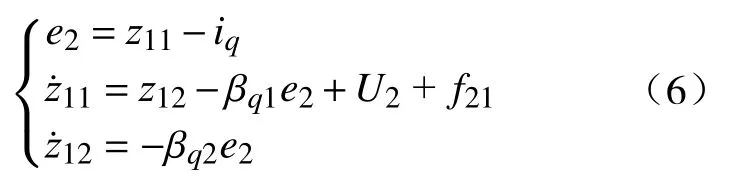
式中：z11为iq的跟踪信号；z12为f22扰动观测值；βq1,βq2为输出误差校正增益。

3）误差反馈控制率设计。

式中：βq3为误差校正增益；u0为输出控制量。

4）扰动补偿。

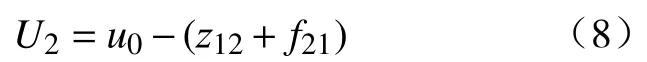
由式（4）～ 式（8）可以设计出改进型q轴电流环线性自抗扰解耦控制框图，d轴电流环的设计也是类似。q轴和d轴的控制框图如图2 所示。

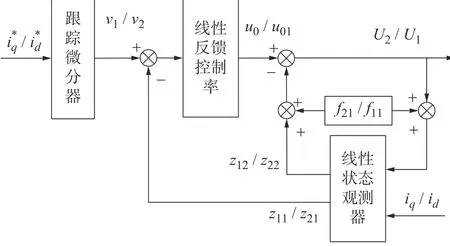
图2 改进型 q/ d 轴电流环线性自抗扰解耦控制框图

3 线性自抗扰控制速度环设计

速度环采用一阶线性自抗扰控制器，提高其抗负载扰动的能力。在d-q轴系下，由式（1）可以得到PMSM运动方程为

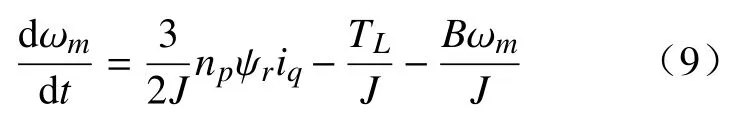
将式（9）中的iq视为控制量u，设综合扰动项为f(t)，令

将式（10）代入式（9），可得

对于综合扰动项f(t)，利用ESO 对其进行观测。设计一阶线型自抗扰速度控制器，具体的设计步骤与电流环类似。可以得到具体的控制律，即：

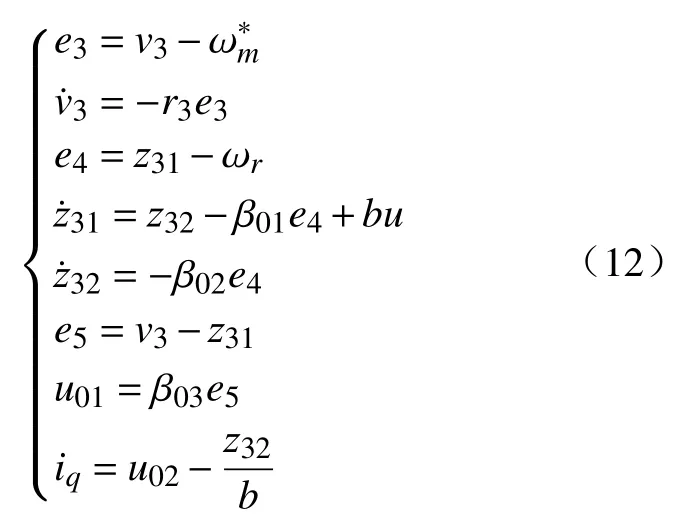
根据以上设计，可以搭建出控制系统结构图如图3 所示。

图3 控制系统结构框图

4 仿真试验与结果分析

为验证本文控制算法的调速性能，在Simulink中搭建采用本文控制器的PMSM 调速系统以及采用传统PI 前馈解耦控制器的PMSM 调速系统，进行仿真对比研究。电机参数如表1 所示。

表1 电机参数

对于传统PI 控制系统，转速环和电流环均采用PI 控制器。速度环的PI 参数为kpv=10，kiv=200；d轴电流PI 控制参数为kpd=0.18，kid=50；q轴电流PI 控制参数为kpq=0.18，kiq=50。

针对本文所提出的控制算法，电流环采用两个一阶线型自抗扰控制器，q轴电流环控制器参数为rq=1 500,βq1=1×104,βq2=1×107，βq3=1 000；d轴参数rd=1 500，βd1=6×103，βd2=4×107,βd3=500。速度环采用一阶线型自抗扰控制器，其控制器参数为r3=1 500,β01=1×104,β02=6×106,β03=20；b由电机参数可以计算，b=4.983 4。

转速跟踪仿真试验：电机空载运行，初始参考转速为3 000 r/min；在0.5 s 时参考转速突变为5 000 r/min；在1 s 时参考转速突变为6 000 r/min；在2 s 时参考转速下降为5 000 r/min；最后在2.5 s 时，参考转速变为0。从图4 可以看出，采用传统PI 控制算法进行速度跟踪时，系统具有较大的超调量；采用本文所提出控制算法，系统不仅响应速度相对较快，而且可以做到无超调跟踪。

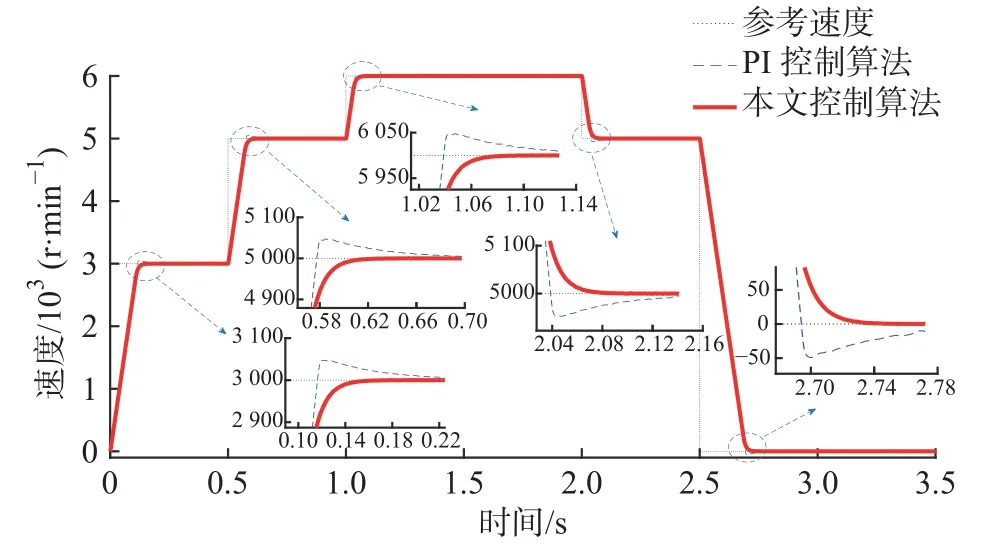
图4 转速跟踪曲线

突加突卸负载仿真试验：电机空载启动，设定转速为6 000 r/min，在1.5 s 时（图5a）中A点），突加160 Nm 的负载，在2.5 s 时（图5a）中B点）将载荷卸去。表2 分别计算了图5a）中加卸载荷时两种控制方法的速度超调量。从图5a）和表2 对比可以看出，在速度上升期间，本文所提出的控制算法能够无超调的跟踪速度指令，同时达到稳态所需时间短。在加卸载荷时，采用本文控制算法，系统具有较小的超调量，能更快的恢复稳定。

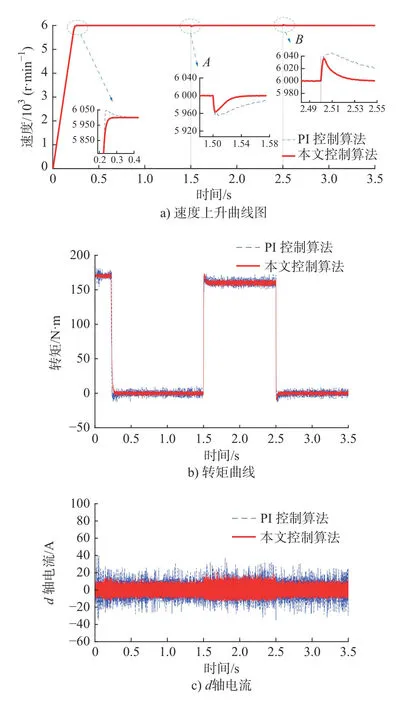
图5 加载和卸载时仿真结果

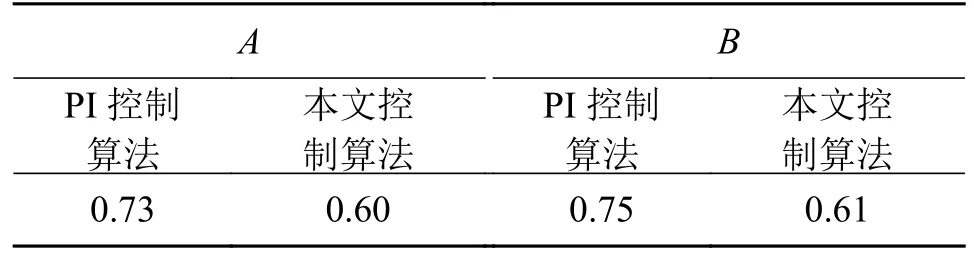
表2 负载变化时速度超调量 %

图5b）和图5c）分别表示的是系统的转矩和d轴电流曲线图。从中可以看出，采用本文控制算法，系统的转矩波动和d轴电流波动相对较小，而且转矩超调减小，说明本文控制算法能够更好的对电流进行解耦控制，改善了系统电流响应性能。

5 结论

1）本文所提出的控制算法能够降低系统的转矩波动和电流波动，改善了电流环的解耦性能；

2）本文所提出的控制算法能够减小系统的速度超调量，加快系统的响应速度。极大的改善了电机的调速性能。