一种考虑拥挤度的布线模型及其算法
2015-12-29陈秀华
陈秀华
(福建船政交通职业学院公共教学部,福建福州 350007)
0 引言
在超大规模集成电路(very large scale integration,VLSI)设计中,布线是在规定的布线区域内实现电路内部各个模块之间的物理连接,它是VLSI物理设计(physical design)中非常关键的步骤之一.当前,超大规模半导体芯片的主流制造技术已经向深亚微米(very-deep-submicron,VDSM)及纳米推进,集成电路设计的集成度和复杂性越来越高,设计规则尺度缩小,使得集成电路中由器件占主导地位变为互连线占主导地位.如果在设计中不能充分考虑布线问题,设计性能就会出现严重偏差,从而反复迭代,使设计的周期变长.
布线问题是NP完全问题,研究者提出许多解决布线问题的算法,这些算法通常分为三类:串行布线、并行布线和多级层次布线.串行布线主要有李氏算法(Lee-algorithm),线探索算法(Line search),基于Steiner树的算法等.李氏算法[1]于1961年由Lee提出,是寻找两点间连接路径的最广泛使用的算法,实际上就是图论上求最短路径的算法.许多人对该算法进行改进以提高其布线效率[2-3],形成一类统称为迷宫算法的布线算法.线探索算法[4]主要思想是用直线代替点进行搜索.基于Steiner树的算法[5-6]目标是构造一棵最小直角Steiner树,用启发算法求得近似最优解.并行布线算法则考虑所有线网布线,通常使用基于网络流和整数规划的算法.文献[7]提出一种用多商品流模型并行布线的算法,文献[8]提出一种0-1整数规划的层次式并行布线算法.而多级层次布线算法同时具有串行和并行布线的特点,把线网分成多级,每一级彼此独立的并行布线,级间串行布线.Cong等[9]提出一种多级布线系统MRS,在此基础上许多研究者又提出改进的多级层次布线算法[10-14].
传统的布线算法分成两步:总体布线和详细布线.总体布线把线网分配给布线区域,为每个线网生成一个布线路径.详细布线根据设计规则确定每个线网实际的通道和过孔[15].在完成所有线网的总体布线后进行详细布线.由于总体布线结果不是详细具体的线网走线,建立的布线资源模型不够精确,使得详细布线往往不能很好地进行.传统的总体布线和详细布线两个步骤不能够处理超大规模芯片上的电路,必须采用分而治之的方法,把整个芯片分成几个部分同时进行布线[16].
本文提出增加总体布线和详细布线间的交互性,使用多种策略来优化布线结果,得到更为准确的布线资源估计,最终减少拥挤度,提高布通率.采用标准的测试例子集对所提出的方法进行测试,以证明该算法的有效性.
1 布线模型
1.1 问题描述
布线过程是对每一条线网进行布线区域的分配.总体布线为每条线网生成一个宽松的解,就是为每条线网分配一些区域,但是不决定实际走线位置[17].详细布线决定每个布线区域中实际走线位置,在总体布线分配的区域中完成布线.
总体布线问题定义为[18]:给定一个网表N={N1,N2,…,Nn},和一个总体布线图G=(V,E),对∀Ni∈N,1≤i≤n,找到一棵斯坦纳树Ti,使得

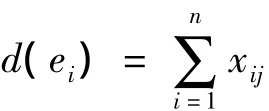
布线算法的目标是在满足各种约束条件下,为每个线网分配合适的通道.算法成功后生成的是连接各线网的子图[19].
输入:1)电路的网表,包括每个线网的源点和漏点;
2)每个器件模块和它的引脚具体位置.
输出:所有线网在版图上的具体走线.
设计目标:
1)最小化总线长和最小化通孔数量;
2)提高布通率、缩短布线时间.
1.2 布线图的数学模型
布线问题是典型的图论问题.每个布线区域所能容下的最大线网数称为布线容量[20],布线容量和布线区域间的关系可以抽象为一张布线图.
本文的布线模型是将整个布线版图抽象为一个逻辑上的布线网格图,整个布线区域被分为h行、w列,得到相应的h×w个布线单元(GRC),每个网格单元组成网格图(grid graph)G,如图1所示.
1)G中的结点集合为V,边的集合为E;
2)每个结点∀v∈V都对应版图中某个布线区域,各线网的引脚都映射到这些结点中;
3)相邻单元对应的结点用边连接起来,每条边e∈E都对应相邻布线区域间的通路,每条边都有一个“布线容量”,用pv表示;每条边的长度和容量都设成相等,网格的大小可以变化,但如果把网格设得太小会增大问题规模[21];
4)每条边e∈E上穿过的线网数量称为已占用容量,用dv表示.
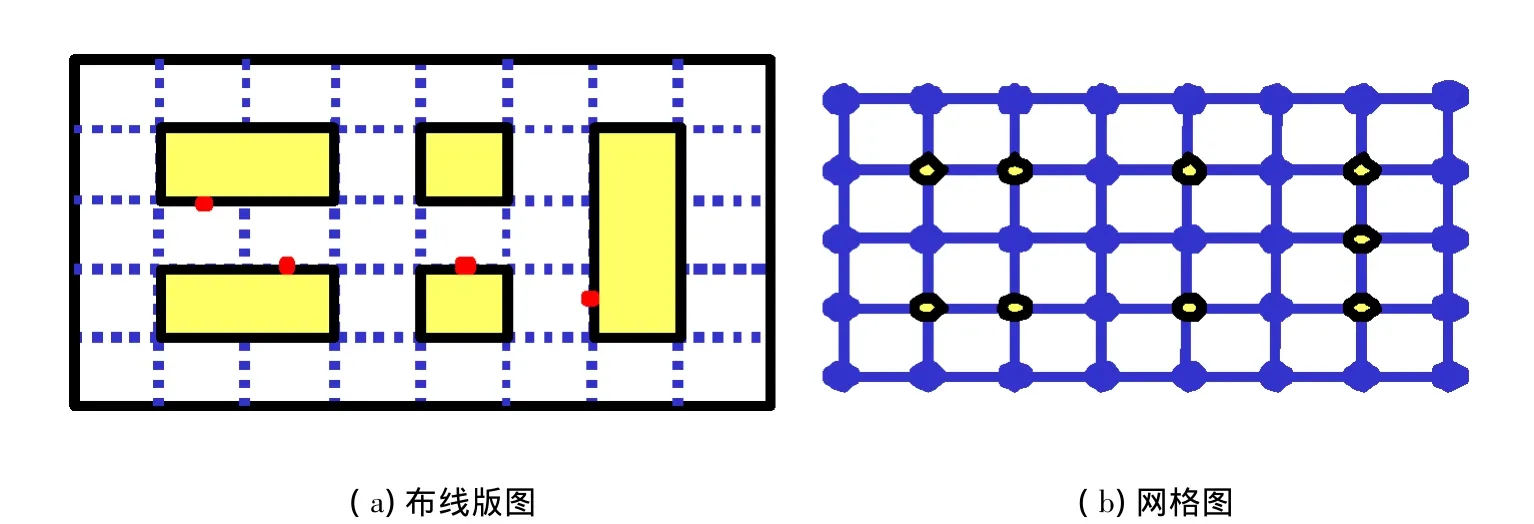
图1 网格图模型Fig.1 The grid graph model
1.3 相关布线模型
总体布线是采用预先设定的模型布线.线网的源点和漏点如果在同一直线上,就用线模型布线;如果失败则改用U模型布线;如果源漏点不在同一直线上,则使用考虑拥挤度的L模型布线(图2(a))和Z模型布线(图2(b)).L模型布线仅搜索两端网络边界框的边,再根据这些边的成本来选择“上L型”或“下L型”,然后进行布线.Z模型布线需要搜索两端边界框的周边及内部边.
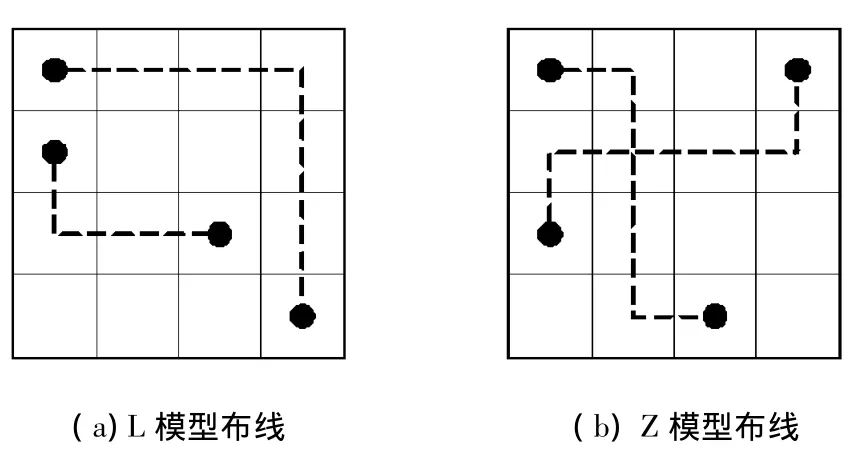
图2 布线模型Fig.2 Routing models
2 算法设计
2.1 算法思想
多级布线算法采用考虑拥挤度的多级布线策略,对每一级里的局部线网交替进行总体和详细布线,增加总体布线和详细布线间的交互性,并且在布线后对资源重新估算,可以得到精确的资源使用结果;同时引入了拥挤度代价函数,将每条备选路径经过的边的布线容量、占用容量和拥挤度等指标通过代价函数,作为选择布线解的依据,选取拥挤度代价最小的路径;最终减少拥挤度,缩短布线时间,提高布通率.
2.2 代价函数
在总体布线阶段应该考虑避免某些布线区域的过度拥塞,引入拥挤度cv:

由于是多级布线,每个布线小区域会有水平拥挤度和垂直拥挤度.在本文中,水平方向布线通道拥挤度即为水平拥挤度,垂直方向布线通道拥挤度为垂直拥挤度.pv,dv分别表示结点v的通道容量和已占用容量.总体布线代价函数为:

用考虑拥挤度cv的代价函数来指导L和Z模型布线,从可行的路径(pv>dv)中选一条代价最小的.而U模型布线,将只考虑线长.在最短线长的情况下考虑拥挤度影响,不增加线长,使接下来的详细布线更容易.如果详细布线成功,dv将被更新,若不成功,则把线网放在最后的重新布线阶段处理.
2.3 算法描述
首先,把输入的多端线网,采用最小生成树法,分成两端线网进行布线.接着,根据线网数量的规模设定布线的级数,把布线区域分成等高宽的布线小区域并确定局部线网,每一级里局部线网间相互独立地进行总体布线和详细布线.对线网采用通孔最小化点到路径的李氏算法进行详细布线,先期得到布线结果,从而降低布线规模,并使用考虑拥挤度的多级布线策略和资源重新估算策略,提高布线资源估计的准确性.
2.3.1 考虑拥挤度的多级布线策略
把布线区域分成等高宽的布线小区域(小方格,tile),如图3中的G0所示.在G0层小区域数量多,问题规模大,难以解决.为了缩小规模,按照“把Gi层4个组成田字形的小区域合并成Gi+1的一个新区域”的策略对小区域进行合并,得到新的G1层;如果G1规模还太大,继续合并,直到满足要求的Gk层.对Gi(0≤n≤k)层中的所有局部线网(源点和漏点都在同一个小区域里)进行总体布线和详细布线,根据式(1)和式(2)用考虑拥挤度cv的代价函数来指导L模型布线(图2(a))和Z模型布线(图2(b)).接着在下一级里,找出那些因为合并而增加的局部线网进行布线.每一级布线针对新增局部线网,都进行总体布线、详细布线和下一级布线资源的估计,直到把整个芯片的布线区域合并成为一个布线区域,最后再把那些布线失败的线网重新进行全局迷宫布线.整个过程如图3所示.
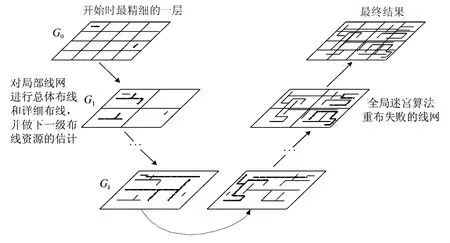
图3 多级布线框架图Fig.3 Multilevel routing framework
2.3.2 资源重新估算策略
多级布线在G0级时计算每个小区域的水平通道容量和垂直通道容量.由于已布线网、通孔和电路模块会占用通道容量,用扫描线法测出已占用容量.接着在总体布线过程中,每完成一条两端线网,就在选择路径上已占用容量加一.但总体布线不是线网的实际走线,并不能精确反映资源使用情况,因此在每级详细布线结束后,需要重新估计资源,再次使用扫描线法重新测量已占用容量,那些在同一水平线或垂直线上的线网只会占用1个单位的通道容量.重新估计资源后,可以相应更新线网的拥挤度.
2.3.3 多级布线算法的伪代码
中南大学在2016级、2017级冶金、工管、能器、机械、临床等非计算机专业约840名学生的“数据库技术与应用”课程进行了连续两年交叉融合的教学模式的实践,课程共48课时,为期12周,获得了比对效果较好的应用数据。
多级布线算法(见表1)的伪代码描述中的步骤5~12完成局部线网布线,步骤9采用拥挤度优化的总体布线方法;步骤12是详细布线,引入了通孔优化策略;步骤13重新估计资源,用于提供步骤9中拥挤度更新所需的数据;步骤14对布线仍然失败的线网进行重新布线.

表1 多级布线算法Tab.1 Multi-level routing algorithm

(续表1)
2.4 复杂度分析
总体布线中把G0级的小区域作为布线基本单元,而详细布线的基本单元是由线宽、线间距和通孔间距等几何设计约束计算得出[22].本文的总体布线采用预先设定好的模型布线,包括:线模型布线、U模型布线、L模型布线和Z模型布线.如果以上方法都失败就用求最短路径的李氏算法布线.李氏算法会搜索很多路径,而这些路径很可能在最后的结果中不会被采用,模型布线只会考虑少数几条路径,时间复杂度会大大减小,比如L模型布线只会考虑两条路径.具体选哪条,会根据代价函数计算得出.
假设:一个两端线网n={(x1,y1),(x2,y2)} ,网格图G=(V,E);
U模型布线时间复杂度根据划定的布线区域不同而不同.
3 实验结果
在主频1.8 GHz,内存2 G的Linux操作系统下用C++实现了该多级布线算法.用文献[9]提供的11个标准电路和设计规则进行测试,表2列出测试电路集的具体信息.对比算法选取经典的MRS算法[9](运行环境与本文算法相同),及其改进算法[11](在SUN Sparc Ultra-60工作站上用C++实现).

表2 测试电路集Tab.2 The benchmark circuit information
表3给出几个布线算法的实验结果,可以看出,本文算法布线结果在布线时间、布通线网数、布通率等方面比MRS布线算法[9]有明显提高.相较于文献[11]的算法,本文算法具有更好的布通线网数和布通率,而在布线时间方面,由于运行环境不同,不具有可比性.
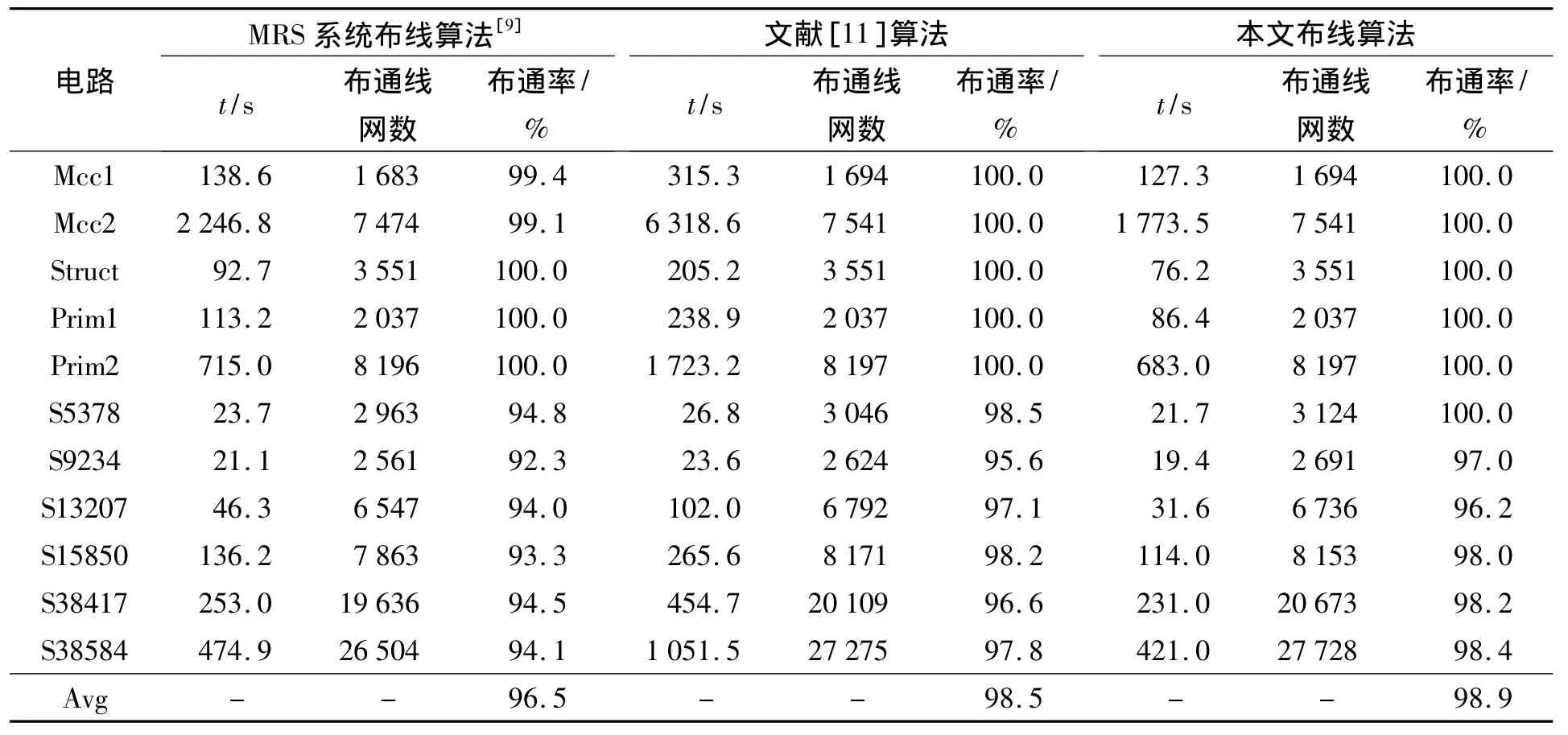
表3 布线结果Tab.3 The routing result
1)在布线时间上,对于表1中的所有实例,本文算法都比MRS算法明显缩短.11个电路布线时间平均缩短14.5%,有6个实例缩短的布线时间超过了10%,在Mcc2、Prim1和S1320711三个电路上的布线时间缩短超过了20%,其中S1320711布线时间缩短了31.7%.
2)在布通线网数上,本文算法在表中所有实例的布通线网数相对于MRS算法都有明显增加,在S5378、S9234和S38417三个电路上布通线网数的增加超过了5%,其中电路S5378增加了5.4%;相较于文献[11]的算法,本文在测试电路中也获得了更好的结果,平均布通线网数更高,在Mcc1、Mcc2、Struct、Prim1、Prim2五个电路上完全布通,在S5378、S9234、S38417、S38584四个电路中都明显增加,布通线网数平均增加了2.4%.
3)在布通率上,本文算法所有测试电路的平均布通率为98.9%,MRS算法的平均布通率为96.5%,文献[11]算法的平均布通率为98.5%.本文算法有6个电路布通率达到了100%,MRS算法只有3个电路布通率达到100%,文献[11]算法只有5个电路布通率达到100%,相对文献[11]算法另外有4个电路布通率明显提高;其中在电路S5378上,本文算法的布通率相对其他两种算法分别提高了5.2%和1.5%.
4 结语
1)在分析传统布线算法的基础上,提出一种总体布线和详细布线交替进行的多级布线算法,在每一级布线中对局部线网进行总体和详细布线,增加总体布线和详细布线间的交互性,利用代价函数,使用多种策略来优化布线结果,得到更为准确的布线资源估计,最终减少拥挤度,提高布通率.
2)采用标准的测试例子集对所提出的方法进行测试,说明了该算法的有效性.但本文的多级算法尚未考虑关键路径的时延约束等方面的优化,将在以后工作中加以研究和改进.
