高压氢氧火箭发动机推力室燃烧稳定性分析

刘 倩，李敬轩，孙纪国，梁炫烨，向小林，潘 亮，郑孟伟

(1.北京航天动力研究所,北京 100076； 2.北京航空航天大学 宇航学院，北京 100191)

0 引言

高压氢氧火箭发动机具有大推力、高比冲等系列优点，是重型火箭芯级动力的重要支撑。大推力高压火箭发动机单台推力为百吨量级，燃烧室尺寸显著增加，燃烧室发生高频燃烧不稳定的倾向大大增加，合理设计喷注器结构对于抑制推力室燃烧不稳定的发生具有重要意义。高频燃烧不稳定依据反馈机理通常分为两类，固有机理燃烧不稳定和喷注耦合燃烧不稳定。在喷注耦合声学振型中，推进剂喷注压力和流量振荡起主要作用。而对于固有机理燃烧不稳定，推进剂喷注后的雾化、蒸发、释热等子过程振荡起主要作用，通常需要采用隔板、声腔等稳定装置加以抑制。

对于氢氧火箭发动机，燃烧室稳定装置可以改进不甚稳定的设计方案的稳定性，但对较稳定的方案的稳定性裕度基本没有改进。美国航天飞机SSME和日本LE-7补燃氢/氧发动机设置隔板和声腔仅为防患于未然和减小风险，实际上对无隔板和声腔发动机做脉冲鉴定，证明发动机是动态稳定的。RD-0120、LE-7A高压补燃氢/氧发动机燃烧室没有加隔板和声腔，试验结果证明燃烧稳定。对于氢氧补燃循环发动机推力室，其喷前温度远远超过不稳定边界温度，一般不会出现燃烧不稳定。

在氢氧高压火箭发动机喷注器设计中，通过优选氧喷嘴的声学频率使其与燃烧室各振型声学错频，可有效避免喷注耦合不稳定的发生。但是，在未加隔板和声腔的现有喷注器结构下是否会发生固有机理燃烧不稳定尚未可知。因此，迫切需要开展氢氧高压火箭发动机喷注器固有机理燃烧稳定性分析。

近年来，由于计算机性能、流体力学和燃烧学的高速发展，学者采用数值模拟开展燃烧稳定性预测，复杂的反应机理和燃烧室结构对热声不稳定的预测成本和工程应用带来极大挑战。Urbano等采用可压缩大涡模拟LES模拟分析了德国宇航中心的缩比BKD氢氧发动机的燃烧不稳定，每计算1 ms时间长度需要1×10核时的CPU时间。尕永婧等针对液氧/煤油火箭发动机燃烧室开展了三维非稳态两相燃烧过程的数值仿真，研究表明雾化角为65°时易于在燃烧室中出现爆炸性的可燃气团并导致剧烈的压力振荡。考虑到数值仿真精度、时间成本和工程研制周期间的最优匹配，具有快速预测燃烧稳定性的数值方法在工程研制中极具应用价值。不稳定预测模型可以研究设计参数对燃烧不稳定性的阻尼和激励作用进而预测发动机的稳定极限。文献[18-19]采用解耦法成功预测了剑桥大学钝体湍流燃烧实验台的极限环振荡燃烧不稳定性、ORACLES长火焰燃烧室的燃烧不稳定性，其均准确预测了燃烧不稳定现象，且频率预测精度偏差均小于2%。该解耦方法能够在保证预测精度的情况下，大大降低计算量。

本文充分借鉴该研究思路，以高压氢氧火箭发动机推力室作为研究对象，针对燃烧室热试验中易出现的一纵一切等声学固有频率，开展非稳态燃烧与声学系统解耦的燃烧稳定性预测仿真研究，采用解耦法研究高频燃烧不稳定激励机理以及发展过程，分析不同喷注器结构参数和工况参数下推力室燃烧稳定性。所做工作将为高压氢氧火箭发动机喷注器设计及燃烧稳定性裕度评估提供参考。

1 预测方法介绍与计算模型

1.1 燃烧稳定性预测方法介绍

不稳定燃烧的反馈回路如图1所示，将非稳态燃烧与声学系统解耦，将声学扰动(表现为速度脉动或当量比脉动)下的燃烧响应(一般为燃烧释热率脉动)表征为火焰传递函数。将得到的火焰传递函数代入声学求解器，预测燃烧不稳定性。燃烧稳定性预测计算主要分为两个部分：①采用非定常雷诺平均NS方程(unsteady Reynolds averaged Navier-Stokes equations，URANS)仿真燃烧过程来计算火焰传递函数；②采用COMSOL来计算燃烧室的声学模态，结合计算出来的分布式火焰传递函数，来预测燃烧不稳定性。

图1 燃烧不稳定反馈回路Fig.1 Combustion instability feedback loop

当燃烧室内的流动速度相对较低时，可近似将燃烧与声学计算解耦，此时对火焰的扰动主要来自上游的流量扰动(或速度扰动)。对于带有短喷管的推力室，由于喷管内流动速度较大，为了满足解耦条件，将喷管从马赫数0.3的位置截断，并将出口设为声学阻抗边界条件，通过Magnus展开法计算得到，喷嘴进口可认为是声学闭口条件。由于喷嘴面积总和/燃烧室横截面积远远小于1，且喷嘴内与燃烧室的温差较大，因此喷嘴上游的声学系统可与燃烧室内的声学系统解耦。本模型的计算主体如图2所示。

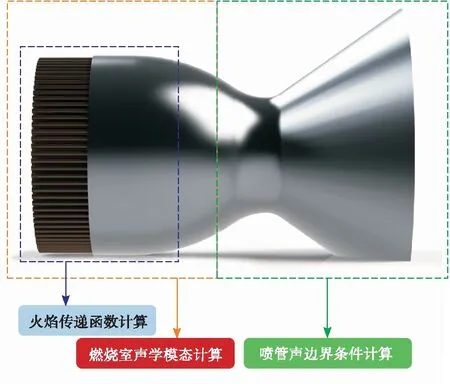
图2 计算组成Fig.2 Computational composition

1.2 喷注单元燃烧过程数值模型

推力室采用液氧/富氢燃气/气氢作为推进剂，采用同轴直流喷注单元同心圆式排列。考虑到计算时间成本，并结合以往计算经验，对单个喷注单元进行URANS数值模拟。下游燃烧计算区域采用圆柱形，径向尺寸采用等效直径法，即其截面积等于所有喷嘴的火焰占据的总横截面积除以喷嘴的数量，求得单个喷注单元燃烧区域的等效直径。考虑到轴向长度对燃烧流场的影响，并综合考虑初步计算得到的火焰长度，燃烧区域长度选取了50倍的氧喷嘴通道直径，见图3。

图3 单喷嘴计算域Fig.3 Single injector computational domain

通过稳态计算获得燃烧室燃烧流场，以此为初始状态，加入质量流量扰动后对喷嘴热释放振荡过程进行瞬态计算。考虑到实际燃烧室的进口和出口声学边界条件非常复杂，压力振荡扰动频率采用最易出现的一纵一切模态预测频率。

采用ICEM划分非结构网格，并进行网格无关性验证，计算了网格数量为1.04×10、2.03×10、4.30×10的3种网格尺度计算，对比燃烧室轴线上的密度分布曲线，其中轴向起始位置为氧喷嘴入口。发现2.03×10、4.30×10的两种网格尺度计算结果接近，故后续选取2.03×10的网格进行计算，见图4。利用商业软件Fluent，采用分离求解器、SIMPLEC算法对压力与速度进行耦合。采用-SST湍流模型、涡耗散模型(eddy-dissipation model，EDM)、化学反应模型。超临界氢、氧以及燃气均按连续相处理，其密度等物性参数采用SRK状态方程，其余物性参数选取NIST的数据进行温度的分段多项式拟合。瞬态仿真时间步长取1×10s，满足Courant-Fredreichs-Lewy(CFL)条件。

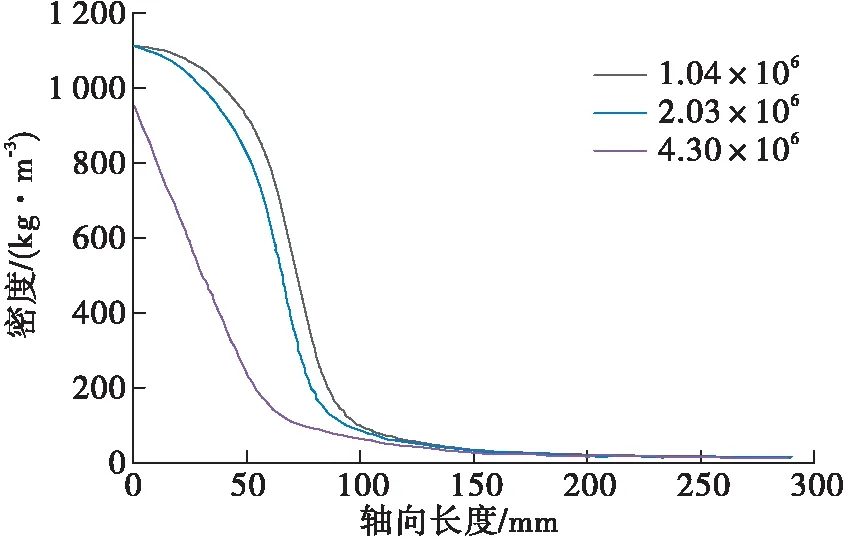
图4 网格无关性验证Fig.4 Grid independence verification

1.3 火焰传递函数计算

由于液氧的密度要远远大于燃气的密度，氧路的阻抗也远远大于燃气路的阻抗，因此在发生不稳定燃烧时，燃料路的流量振荡远远大于氧路的流量振荡，进而引起火焰燃烧释热率发生振荡，与燃烧室声学系统耦合，产生燃烧不稳定性。故在燃气通道施加质量流量扰动，分析下游火焰流场各参数的变化，并计算火焰传递函数，开展燃烧不稳定性预测。

在燃气通道对流量施加正弦扰动，入口扰动形式为

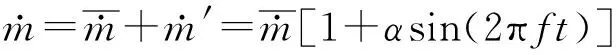
(1)

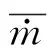
对于液体火箭发动机同轴直流喷嘴，其稳态火焰长度与燃烧室内声波波长处于同一个量级，因此在预测燃烧稳定性时火焰不能被认为是轴向紧凑型的，需要考虑分布式火焰传递函数。通常当分段后火焰长度不大于声波波长的0.1，可认为其远远小于声波波长，符合紧凑火焰假设，可以开展燃烧稳定性预测。

将火焰分段后各段的火焰传递函数定义为

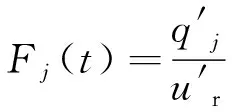
(2)

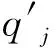
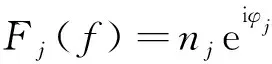
(3)

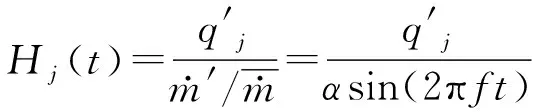
(4)

从进口质量扰动到参考点速度扰动之间的传递函数为

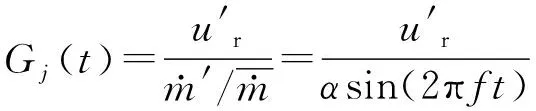
(5)

结合式(4)和式(5)，即可获得火焰传递函数式(2)。

1.4 燃烧室声学模态计算

利用COMSOL软件对整个燃烧室建立Helmholtz方程。通过耦合Helmholtz方程和火焰传递函数，结合进、出口处的声学边界条件，求得整个系统的声学模态，表达式为

(6)

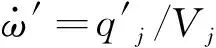
将燃烧室几何体与喷注单元六段式的分布式火焰的几何模型进行装配，求解整个系统的Helmholtz方程，即可预估推力室内各个模态的频率和压力分布。其中，计算区域介质的平均温度、平均密度和平均声速采用URANS仿真得到的结果，比热容比采用REFPROP软件来计算。对几何模型采用非结构化网格进行划分，网格数为1.06×10，如图5所示。

图5 声学模态计算模型及网格划分Fig.5 Acoustic modal calculation model and meshing

燃烧室的固有频率主要取决于燃烧室的结构尺寸及其内部介质的热力学参数，火焰扰动对声学模态频率的影响较小，主要影响声学模态的稳定性。计算声学模态的特征值为复数，实部为模态频率，虚部为增长率。当虚部大于0时，主要物理量如压力脉动幅值逐渐减小，燃烧室在该声学模态上是稳定的；当虚部小于0时，压力脉动幅值逐渐增大，燃烧室在该声学模态上是不稳定的。

2 结果与讨论

2.1 稳态计算结果

通过稳态燃烧计算得到火焰长度约为0.29 m，绝热火焰温度约为3 742 K，见图6。稳态计算流场参数分布曲线见图7，其中轴向长度起始位置为燃烧室喷注面板。平均温度沿轴线逐渐增加，到轴向长度220 mm后温度基本保持不变；平均密度沿轴线先下降后趋于平缓；平均声速呈先减小后增加趋势，主要与组分和温度等相关。初步预测的一纵一切模态的频率为3 767 Hz(见图8)，将该一纵一切模态计算频率作为计算火焰传递函数时入口扰动频率的参考。

图6 喷嘴燃烧温度场分布Fig.6 Temperature distribution of injector combustion

图7 单喷嘴燃烧室稳态燃烧场计算Fig.7 Calculation of steady-state combustion field parameters of single-injector combustor

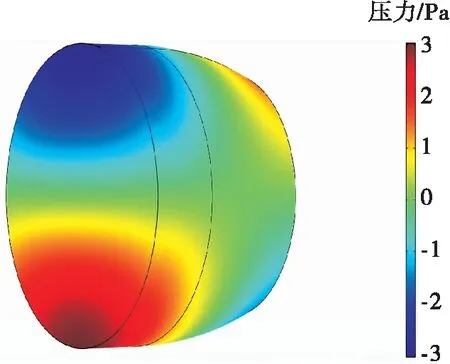
图8 一纵一切模态压力分布Fig.8 First-order longitudinal first-order tangential modal pressure distribution

2.2 非稳态燃烧计算结果

根据燃烧室的平均声速(1 562.1 m/s)和预测的一纵一切声学频率(3 767 Hz)，可得燃烧室声波波长约为0.41 m。结合仿真计算火焰长度0.29 m，将火焰沿着轴向分为6段，利用此6段区域的热释放速率可近似代表燃烧室内所有的热释放速率。

通过开展单喷注单元的非稳态燃烧仿真计算，获得不同参数在一个周期内的分布云图，见图9。燃烧释热率主要分布在喷嘴出口处，成蝌蚪状，并在约220 mm处消失。在一个周期内，“蝌蚪头部”的释热率幅值产生周期性变化，“蝌蚪尾巴”也在不断摆动。

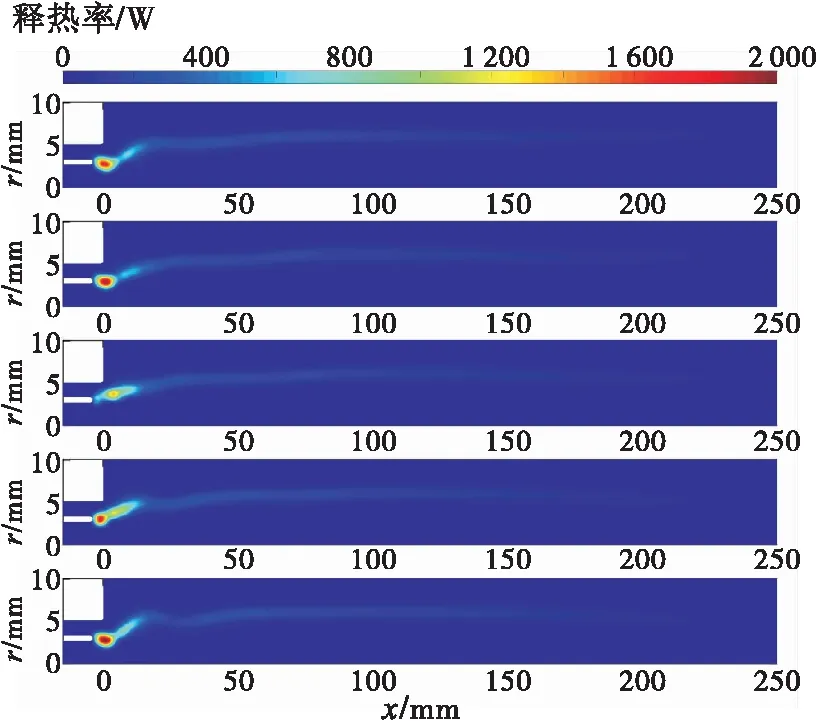
图9 一个周期内x-y平面燃烧释热率的分布云图Fig.9 Distribution cloud map of combustion heat release rate in x-y plane in one cycle

不同轴向位置6个区域的燃烧释热率脉动见图10。释热率振荡曲线接近正弦曲线，但具有不同的振荡幅值和相位，并且第一段的振荡幅度最大，越往后振荡幅度越小。

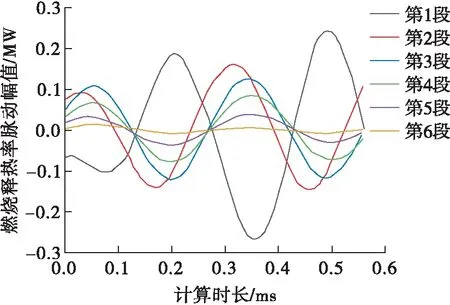
图10 6段燃烧释热率脉动幅值Fig.10 Six-stage combustion heat release rate pulsation

图11为传递函数的幅值和相位，可以看出其幅值在第一段区域最大，然后逐渐降低。

图11 6段质量扰动和释热率之间的传递函数Fig.11 Transfer function from mass perturbation to heat release rate for six regions

图12为不同轴向位置从进口质量扰动到参考点速度扰动之间的传递函数的幅值和相位，其相位的变化较小。其中参考位置选为=-12 mm到=-4 mm的平均值。结合式(2)、式(4)、式(5)，获得分布式火焰传递函数，如图13所示。

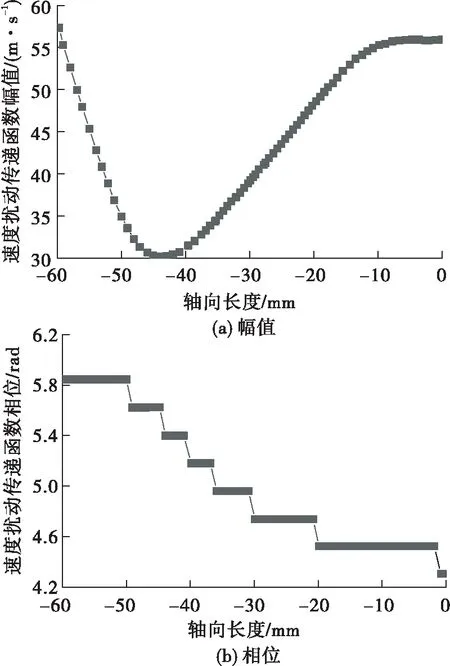
图12 不同轴向位置速度传递函数Fig.12 Velocity transfer functions at different axial position

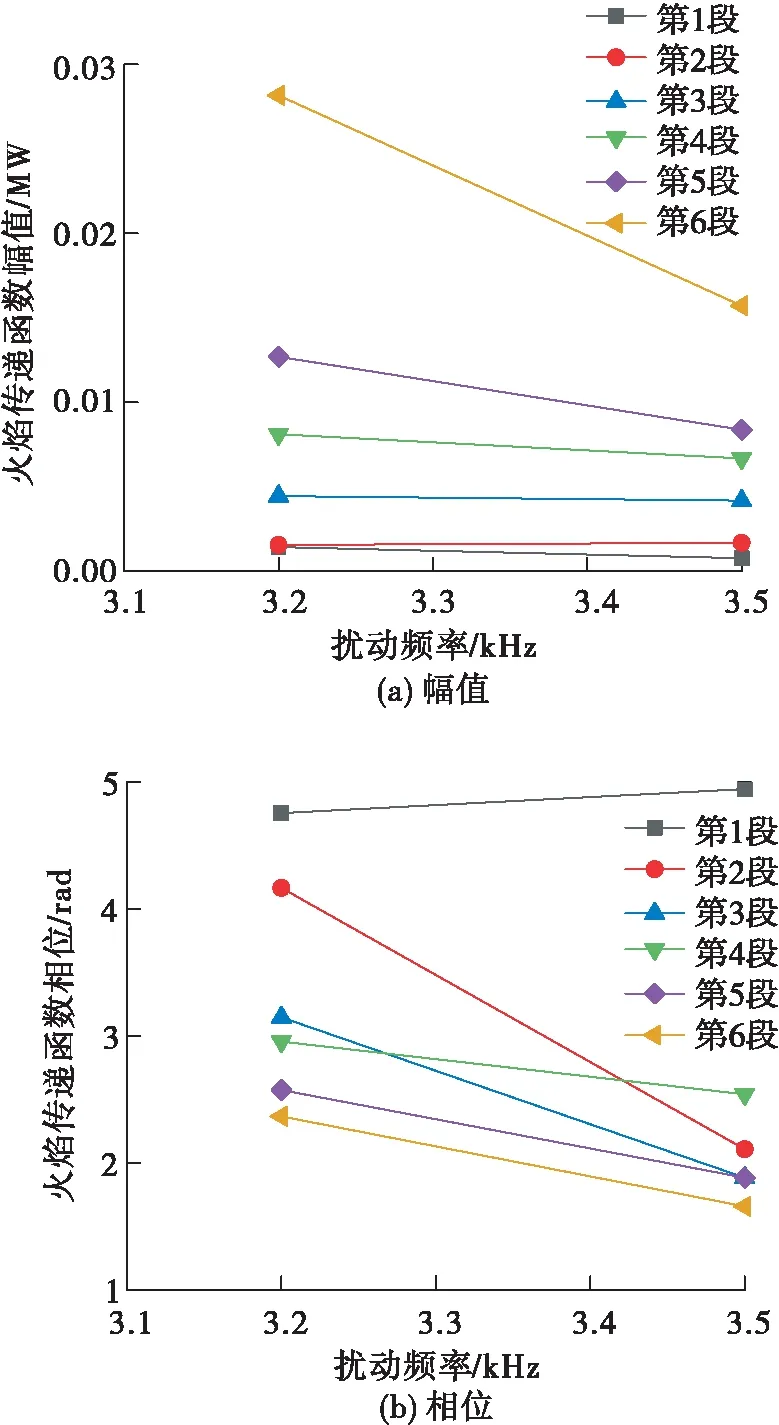
图13 各段火焰传递函数幅值相位图Fig.13 Amplitude phase diagram of flame transfer function of each segment

2.3 燃烧稳定性仿真结果

利用非稳态燃烧与声学系统解耦法计算加载了分布式火焰几何模型，得到一纵一切模态压力分布，如图14所示。

图14 带分布式火焰传递函数的一纵一切模态压力分布Fig.14 First-order longitudinal first-order tangential modal pressure distribution with flame transfer function

随着推力室燃气/氧喷注速度比的增加，燃烧室一纵一切模态频率呈上升趋势，模态增长率也总体呈上升趋势，燃烧过程变得更加稳定，见图15。

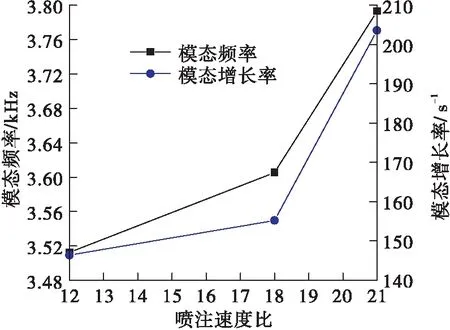
图15 喷注速度比对模态及其增长率的影响Fig.15 Effect of injection velocity ratios on mode and its growth rate

分析原因为随着燃气/氧喷注速度比的增加，燃气的喷注速度增加，喷嘴出口气液相互作用增强，液柱长度减短(见图16)。

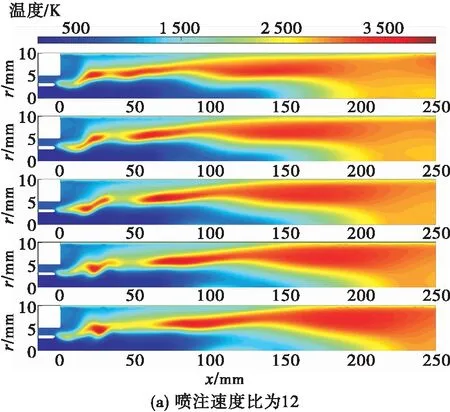
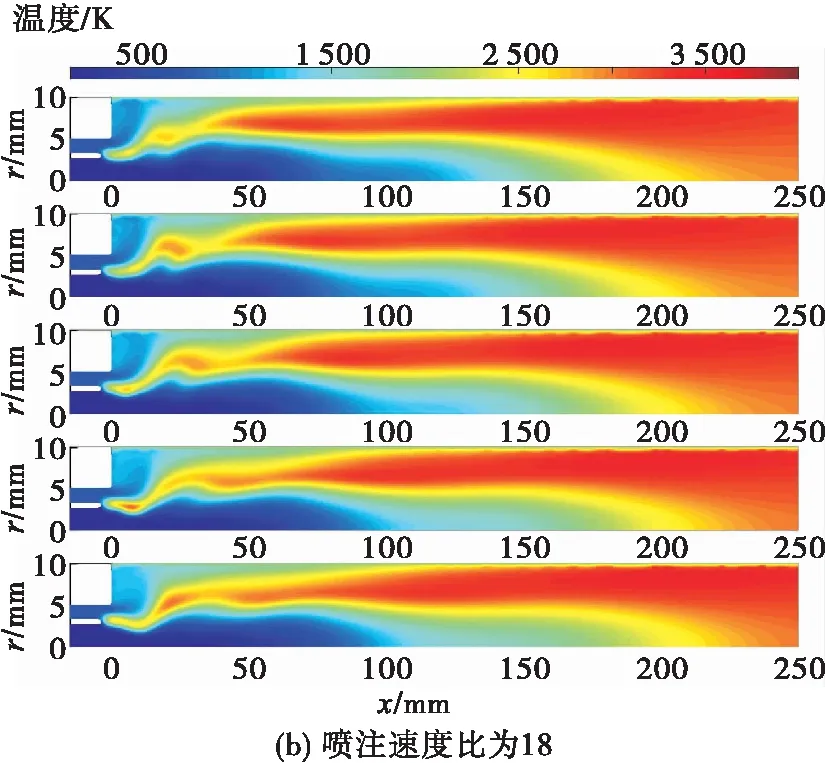
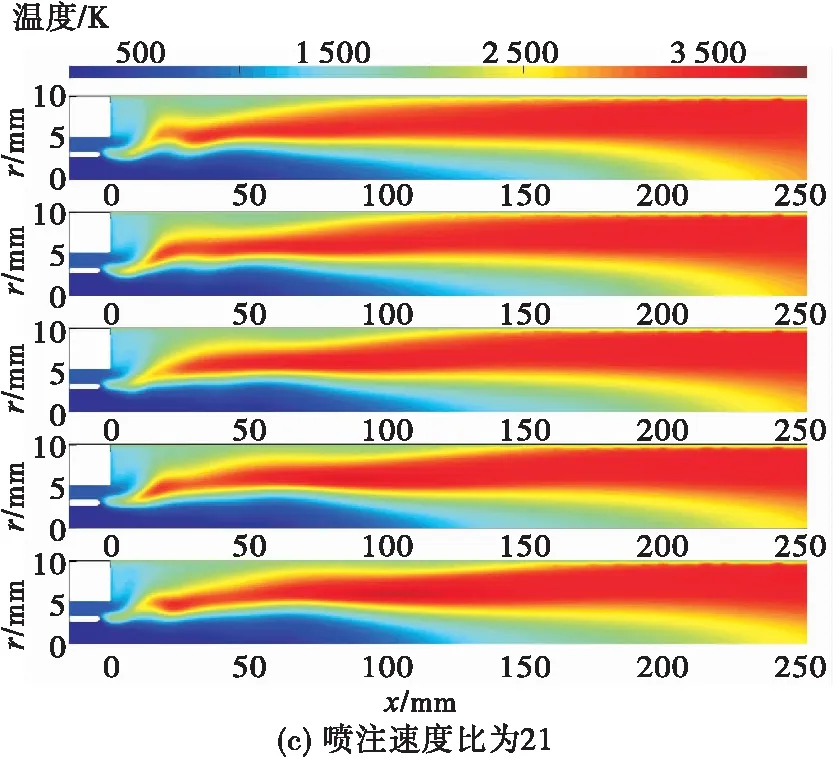
图16 不同喷注速度比下的温度分布云图Fig.16 Temperature distribution under different injection velocity ratios

同时由于燃气的喷注速度增加，燃气在燃烧室中的停留时间减短，燃烧室整体释热区后移，分布式火焰上最大释热率相应减少(见图17)，系统相对而言逐渐变得稳定。

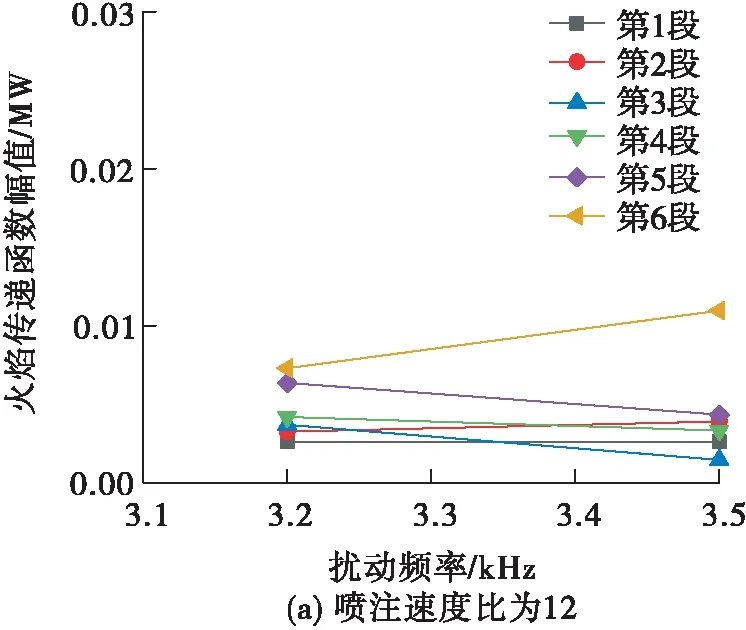
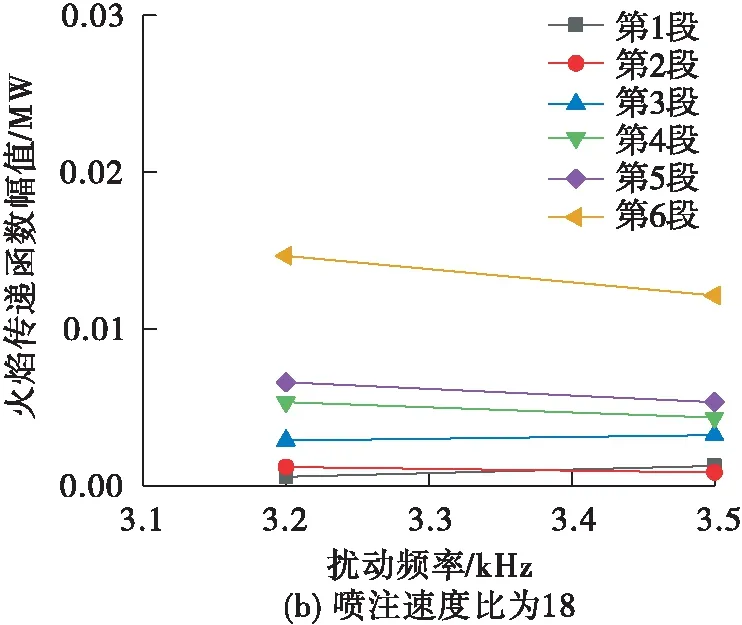
图17 不同喷注速度比下的火焰传递函数Fig.17 Flame transfer function at different injection velocity ratios

随混合比的增大，燃烧室一纵一切模态的频率变化不大，但模态增长率逐渐降低，燃烧室的稳定性变差，见图18。

图18 混合比对模态及其增长率的影响Fig.18 Effect of mixing ratios on mode and its growth rate

分析原因为在不同混合比下燃烧室内的燃烧均为富燃状态，随着混合比的增加，燃烧室中的氧量相对增加，可消耗更多的燃料放热，燃烧室内温度更高，即热释放变得更大，见图19，在液体火箭发动机燃烧室中，由于喷嘴附近为压力波腹，因此此处释热强度增强将使得热声不稳定系统变得更不稳定。

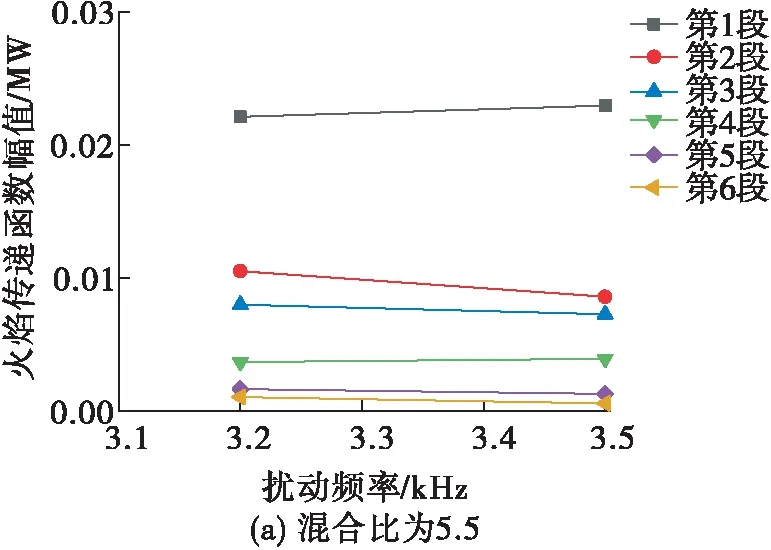
图19 不同混合比下的火焰传递函数Fig.19 Flame transfer function at different mixing ratios

燃烧室相对氧喷嘴压降增大时，推力室一纵一切模态的频率变化不大，增长率略有降低，但影响不大，见图20。这是由于燃烧室火焰较长，为火焰敏感型不稳定，压降的改变主要为边界条件的改变，对燃烧室稳定性影响不大。

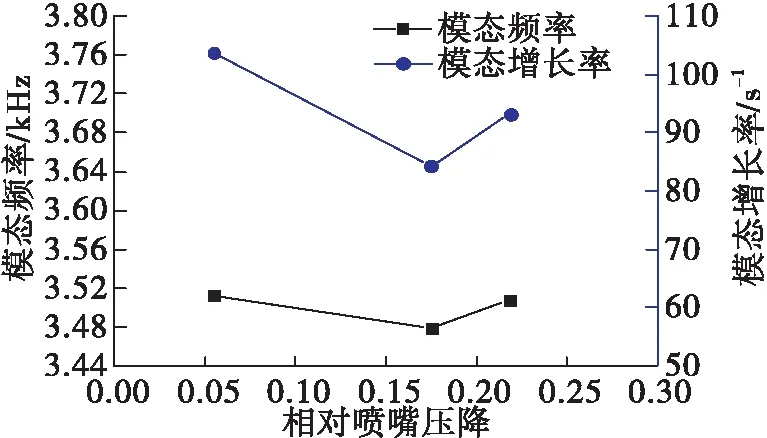
图20 相对喷嘴压降对模态及其增长率的影响Fig.20 Effect of relative nozzle pressure drop onmode and its growth rate

氧喷嘴缩进深度比对推力室一纵一切模态的频率基本无影响。当缩进深度比从0.42增加为0.67时，系统更趋于稳定；但缩进深度比继续增加对稳定性的影响效果相反，即存在一个最优缩进深度比，见图21。

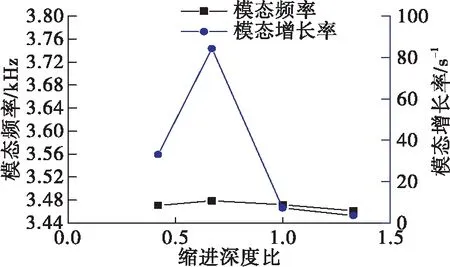
图21 缩进深度比对模态及其增长率的影响Fig.21 Effect of retraction depth ratio on mode and its growth rate

当富氢燃气喷前温度升高时，推力室一纵一切模态的频率变化不大，模态增长率略有降低，但影响不大，见图22。

图22 喷前温度对模态及其增长率的影响Fig.22 Effect of per-injection temperature on mode and its growth rate

3 结论

针对高压氢氧火箭发动机推力室不设置隔板喷嘴和声腔的结构方案，利用火焰传递函数+低阶模型的解耦法，开展燃烧稳定性裕度的仿真预测，针对燃烧室热试验中易出现的一纵一切等声学固有频率，分析了不同喷注参数和结构参数下燃烧室的燃烧稳定性。主要结论如下：

1)在给定工况下预测得到的燃烧室均未出现燃烧不稳定现象；

2)混合比对燃烧室一纵一切模态频率影响较小，但随混合比的增大，模态增长率逐渐降低，燃烧室的稳定性变差；

3)相对氧喷嘴压降对推力室一纵一切模态频率及其模态增长率均影响较小；

4)氧喷嘴缩进深度比对推力室一纵一切模态的频率无影响，但存在一个最优缩进深度比使燃烧稳定性裕度最高；

5)在推力室设计中通过增加燃气/氧喷注速度比或降低燃烧室混合比，有利于提升燃烧稳定性裕度。