超高转速氢涡轮泵柔性转子动特性仿真分析

杜家磊，王怡萱，李 铭，姜绪强，褚宝鑫

(北京航天动力研究所，北京 100076)

0 引言

膨胀循环氢氧发动机具有比冲高、系统相对简单、可靠性高等优点，是运载火箭上面级主动力系统的理想选择。目前，我国成功研制了10 tf级推力的膨胀循环氢氧发动机，保证了探月工程和火星探测等重大工程的顺利实施。随着空间探测和利用规模的扩大，研制用于重型运载火箭的更大推力膨胀循环氢氧发动机势在必行。

氢涡轮泵作为膨胀循环氢氧发动机的核心关键部件，在研制过程中需解决超高转速柔性转子设计的难题。国外具有代表性的先进膨胀循环发动机VINCI和RL60的氢涡轮泵设计转速均高达90 000 r/min，俄罗斯的RD0146发动机氢涡轮泵设计转速更是高达120 000 r/min。超高的转速保证了氢涡轮泵更高的功率密度比，也有助于提高发动机的总效率和推重比；但转子需设计为工作在超临界转速的柔性转子，给临界转速和稳定性控制带来了较大难度。

转子动力学设计中，临界转速的主要影响因素是支承刚度和转子结构，因此，在总体参数限制下的支承刚度和转子结构优化是研究的重点。转子稳定性的影响因素则十分复杂，国内外多型氢氧发动机涡轮泵都曾出现过不同形式的转子稳定性问题。根据相关研究，引起涡轮泵转子失稳的可能因素有：转子零件内摩擦、密封处的流体动压力、轮盘Alford力等。从工程实践来看，任何单一因素都无法完全解释转子实际的失稳现象，这也说明了转子稳定性问题的复杂性。

本文以重型运载火箭25 tf级膨胀循环氢氧发动机(以下简称25 tf发动机)氢涡轮泵的研制为背景，对设计转速80 000 r/min的氢涡轮泵转子的动特性展开仿真分析，建立转子系统有限元计算模型，考虑支承结构参振、密封流体的刚度及阻尼、支承刚度及阻尼随转速变化等因素的影响，计算分析各设计参数对转子临界转速、稳定性的影响，提出改进方向，为转子系统优化和改进设计提供参考。

1 转子总体方案

1.1 转子结构

25 tf发动机氢涡轮泵转子系统设计方案如图1所示，转子由主轴、诱导轮、离心轮、涡轮盘、轴套等零件组成，用滚动轴承支承，并在泵端、涡轮端轴承外设置弹性支承和金属橡胶阻尼器，为转子提供必要的支承刚度和阻尼作用。转子额定转速80 000 r/min，工作在二、三阶临界转速之间。

1-主轴；2-诱导轮；3-离心轮I；4-离心轮II；5-涡轮盘I；6-涡轮盘II；7-滚动轴承；8-弹性支承。图1 氢涡轮泵转子系统Fig.1 Rotor system of the hydrogen turbopump

1.2 计算模型和方法

采用有限元方法对转子系统进行动特性计算，将转子和支承结构划分单元，构建计算模型。对转子部分，根据其结构特点划分为若干个梁单元和圆盘单元，分别建立各梁单元、圆盘单元的运动方程，这里不再赘述；对支承结构部分，将考虑弹性支承的部分结构质量参与振动对转子动特性的影响，如图2所示，把滚动轴承简化为弹簧，弹性支承和金属橡胶阻尼器简化为弹簧和阻尼器，弹性支承参与振动部分则简化为集中质量，建立弹性支承参与振动质量的运动方程，即

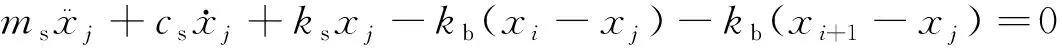
(1)

式中：为参振结构质量，即图2所示虚线框内部分；为轴承刚度；为弹性支承刚度；为阻尼器提供的阻尼；和为节点编号。

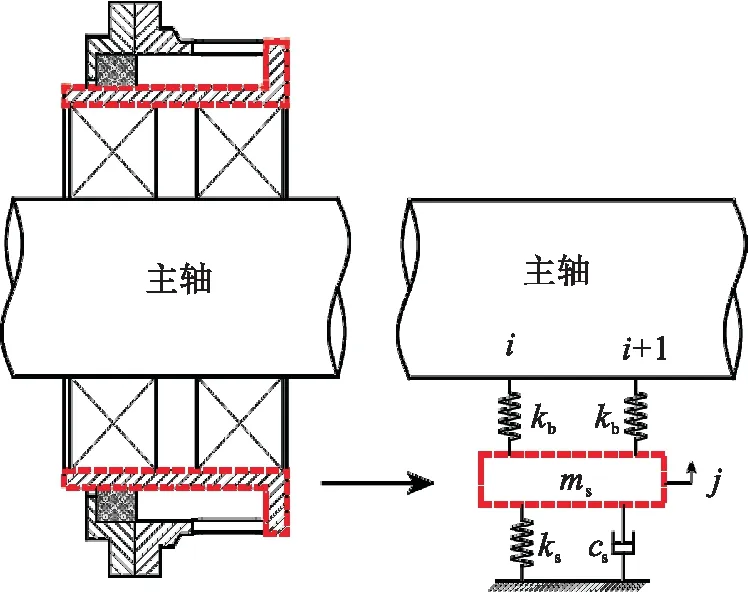
图2 支承结构参振模型示意图Fig.2 Schematic diagram of supporting structure vibration model

考虑支承结构参振的转子系统有限元模型如图3所示。转子上的诱导轮、离心轮、涡轮盘均用圆盘单元表示；主轴的各轴段用梁单元表示，对主轴上有轴套(轮毂)的轴段，则将轴套和相应的主轴轴

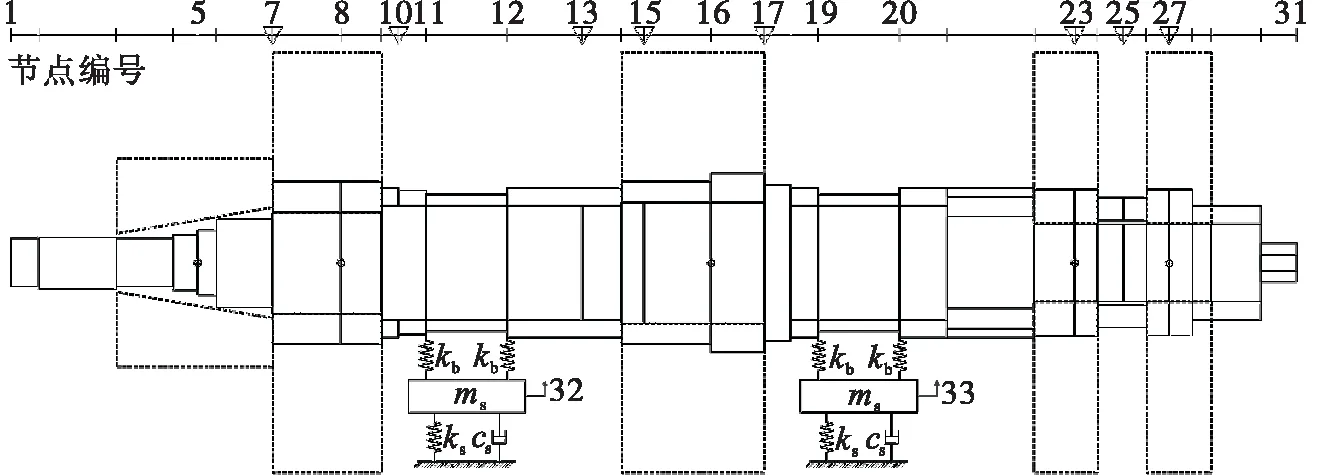
图3 转子系统有限单元模型Fig.3 Finite element model of the rotor system

段等效为具有一定密度和弹性模量的同材质轴段，等效原则是质量和刚度不变；节点处有“▽”的表示该位置有流体密封结构。

将转子各单元和式(1)所示支承结构参与振动的运动方程进行组合得到整个转子系统的运动方程

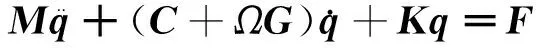
(2)

式中：为系统质量矩阵；为系统陀螺矩阵；为系统阻尼矩阵；为系统刚度矩阵；为转子所受的力向量；为转子转速；为系统广义位移向量。

表达式为

=[1，1，…，(-2)，(-2)，(-1)，，1，
-1，…，(-2)，-(-2)，(-1)，]

(3)

式中：为节点总数；节点1～(-2)为转子上的节点，每个节点有4个自由度；节点(-1)、为支承参振质量节点，每个节点有2个自由度；为位移；为角度。

计算转子无阻尼临界转速和振型时，可将式(2)转子运动方程转化成式(4)所示形式，然后通过一维搜索得到满足式(4)的转速，即为临界转速；之后再计算行列式矩阵在临界转速下的零空间向量，得出转子振型。

det[-(-)+]=0

(4)

对转子进行稳定性分析时，可将式(2)改写成式(5)所示状态方程形式，然后再根据式中的状态矩阵，计算得到转子系统的复频率=+i，并据此分析判断转子的稳定性。

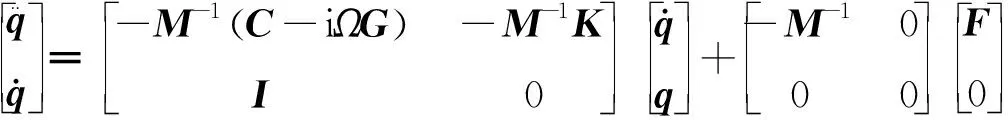
(5)

以图1所示转子系统初步设计方案为基准状态，用图3所示有限元模型，对转子的临界转速和稳定性展开计算分析。基准状态下前述弹性支承刚度为7×10N/m，各处流体密封是齿型结构形式。

2 临界转速计算分析

25 tf发动机氢涡轮泵转子额定转速80 000 r/min，为满足发动机推力调节的需要，工作转速还要在一定范围内可调。转子临界转速的设计目标是保证在整个工作转速区内，转子工作转速与临界转速的间隔裕度不低于20%，同时转子过临界转速时的弯曲应变能比例不高于25%。

计算得到的基准状态下转子前三阶临界转速、弯曲应变能比例如表1所示，相应的转子模态振型如图4所示。

表1 基准状态转子临界转速和弯曲应变能Tab.1 Critical speeds and bend strain energy rates of the reference state rotor

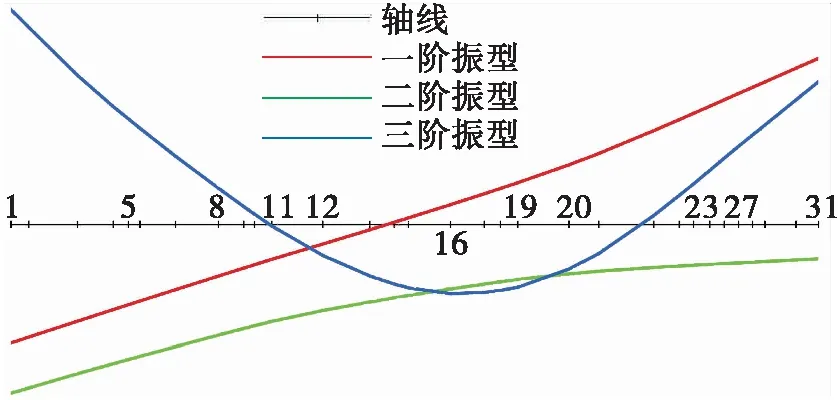
图4 基准状态转子前三阶模态振型Fig.4 First three mode shapes of the reference state rotor

根据表1可知，在基准状态下，额定工况转子工作转速与第三阶临界转速间隔裕度为32%；低工况转子工作转速与第二阶临界转速间隔裕度为30%；工作转速与临界转速的间隔裕度均满足“不低于20%”的要求。为进一步优化转子系统设计，以下进行弹性支承刚度、密封附加刚度、轮盘质量对临界转速的影响分析。

2.1 弹性支承刚度的影响

在转子结构确定的情况下，支承刚度是影响临界转速的主要因素。可通过调整泵端、涡轮端支承刚度来达到临界转速设计目标。以基准状态为参考，计算泵端、涡轮端弹支刚度分别变化时，转子的临界转速变化情况(见图5)。

从图5可以看出：转子的前三阶临界转速均随着支承刚度的增加而增大；比较而言，第二阶临界转速对泵端支承刚度变化更敏感，第一、三阶临界转速则对涡轮端支承刚度变化更敏感；从增强金属橡胶阻尼器作用效果的角度考虑，还可以在基准状态基础上适当降低支承刚度，这样依然能够满足上述临界转速与工作转速的间隔裕度要求。

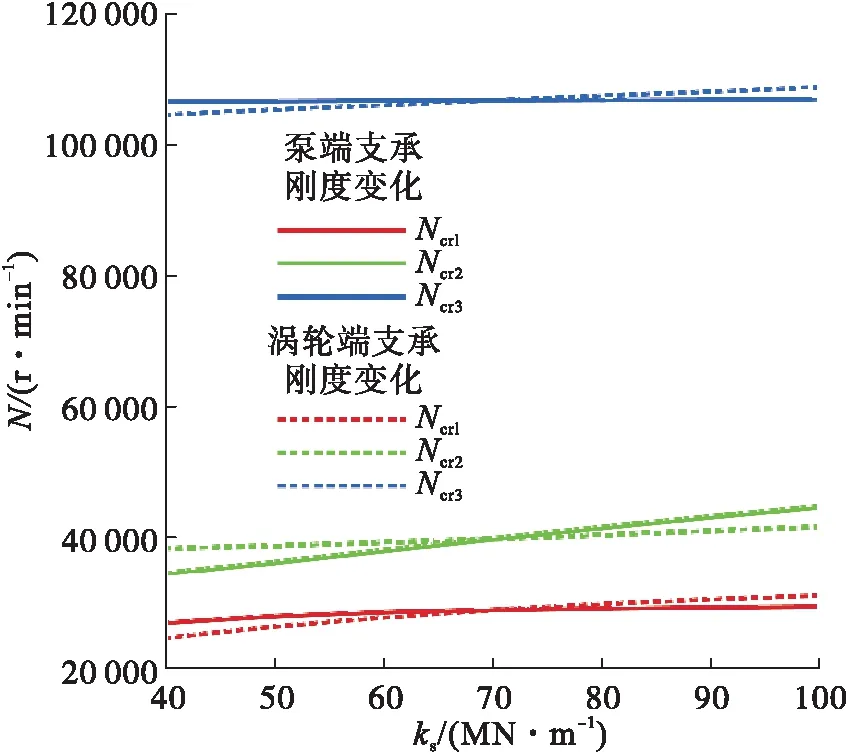
图5 支承刚度对转子临界转速的影响Fig.5 Effect of supporting stiffness on rotor critical speeds

根据图5可知，降低泵端支承刚度可以明显降低二阶临界转速，而三阶临界转速降幅较小，能够满足设计裕度要求，还能扩大二、三阶临界转速间隔，增大转速可调范围；建议适当降低泵端支承刚度。

2.2 密封附加刚度的影响

在25 tf发动机氢涡轮泵的结构设计中，图3所示节点7、10、13、15、17、23、25、27处是转子与壳体间的流体动密封所在位置。涡轮泵工作时，密封处的流体作用力会对转子产生附加支承刚度和阻尼，这对转子的动特性有一定影响。

通过密封流场仿真计算得到的上述密封流体在额定转速80 000 r/min下的附加刚度及阻尼系数如表2所示。

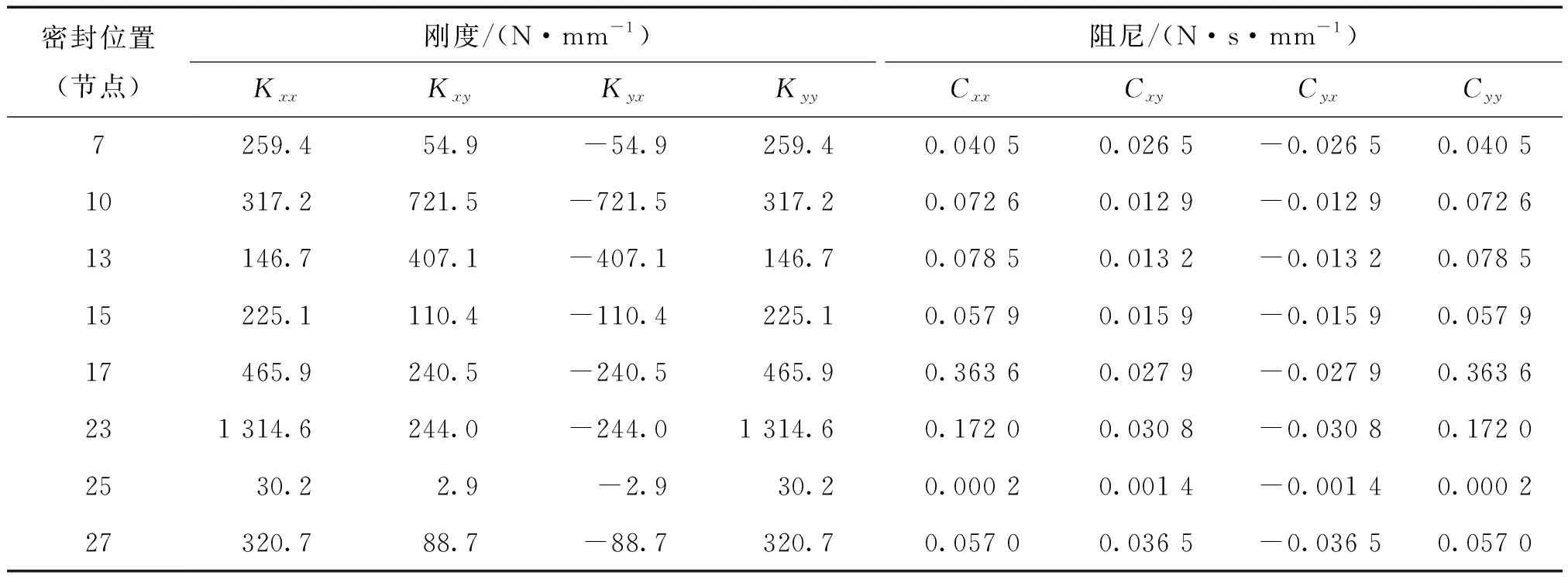
表2 额定转速下密封流体对转子的附加刚度及阻尼Tab.2 Additional stiffness and damping from seal fluid at rated speed

假设转速为0时，密封对转子的附加刚度及阻尼也是0，随着转速的升高，各处密封流体对转子的附加刚度及阻尼均线性增加。考虑密封处流体附加刚度及阻尼作用及其随转速的变化，计算得到的转子临界转速与基准状态不考虑附加刚度及阻尼时的临界转速对比如表3所示。

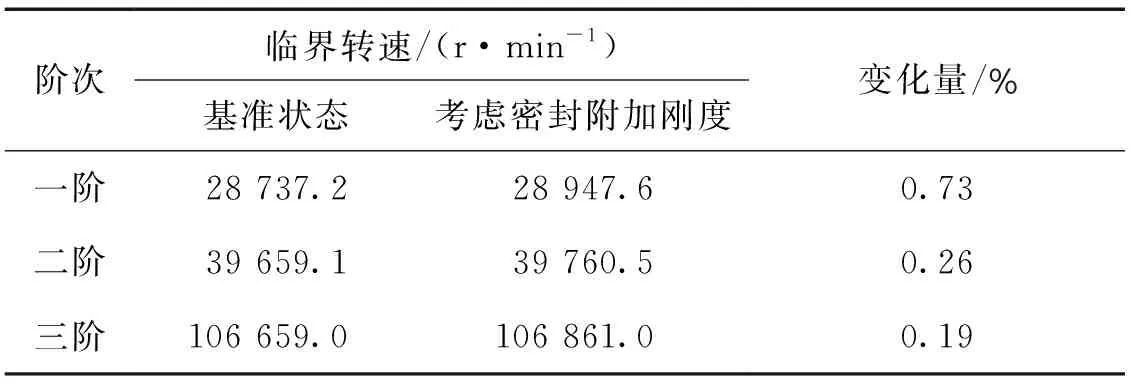
表3 考虑密封流体附加刚度及阻尼的临界转速Tab.3 Critical speeds considering the effect of additional stiffness and damping from seal fluid

从表3可知，考虑密封流体附加刚度作用的情况下，转子前三阶临界转速都略有增大，但增加都不明显，相对增加量都低于1%。主要原因是密封的附加刚度很小，与转子主支承刚度相比要低2个数量级。因此，在临界转速初步设计时可不考虑密封附加刚度的影响。

2.3 轮盘质量变化的影响

诱导轮、离心轮、涡轮盘作为转子上具有较大质量的轮盘类零件，其质量属性是影响转子临界转速的重要因素。以轮盘设计参数为基准，计算了轮盘类零件的质量(包括转动惯量)参数分别在原有基础上变化±10%时，转子前三阶临界转速的变化情况，结果如图6所示。

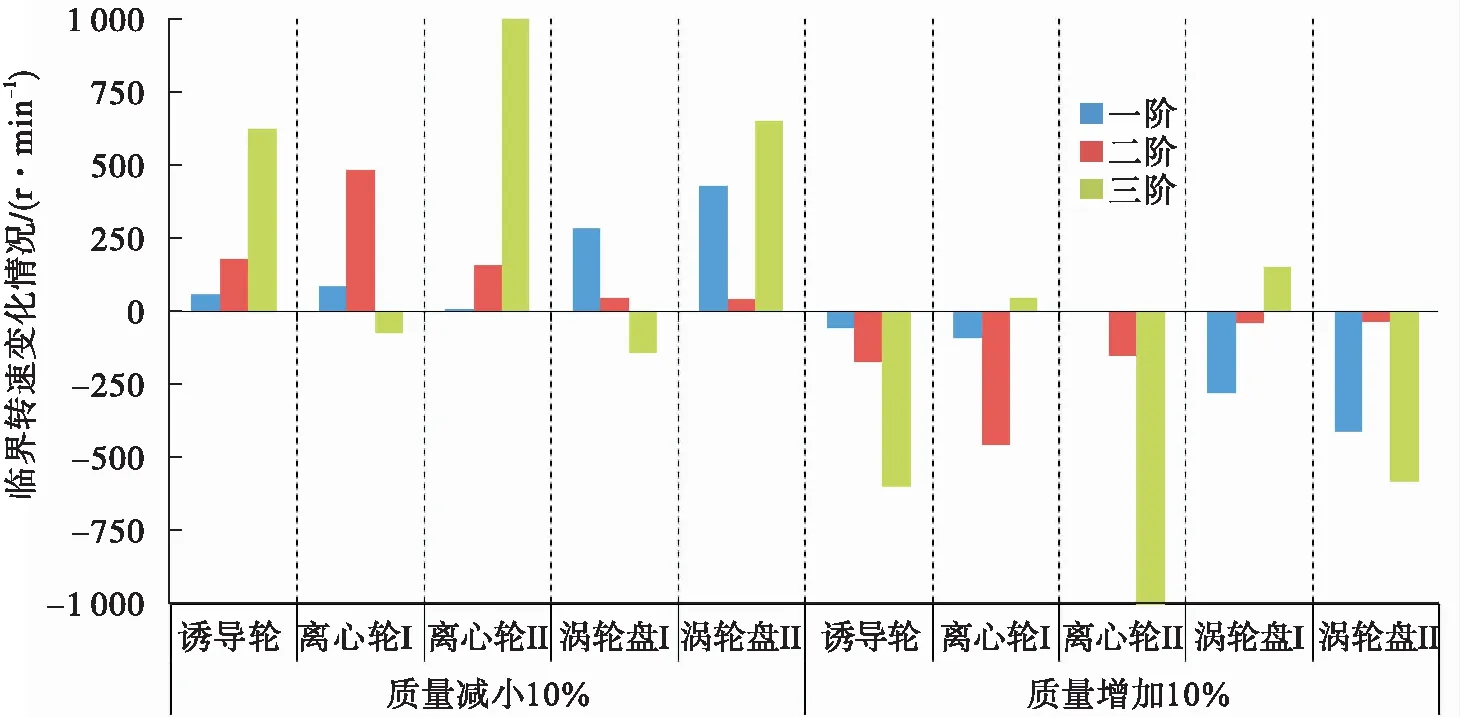
图6 轮盘质量变化对转子临界转速的影响Fig.6 Effect of blade disk mass variation on rotor critical speeds

从图6可以看出：涡轮盘Ⅱ的质量变化对一阶临界转速的影响最大，其质量增加10%，一阶临界转速降低400 r/min左右；离心轮Ⅰ的质量变化对二阶临界转速的影响最大，其质量增加10%，二阶临界转速降低450 r/min左右；离心轮Ⅱ的质量变化对三阶临界转速的影响最大，其质量增加10%，三阶临界转速降低1 000 r/min左右。离心轮Ⅰ、涡轮盘Ⅰ的质量增减对转子三阶临界转速的影响趋势与其他相反，即质量增加转子三阶临界转速反而增大；这可能是由于这两个轮盘都在轴承外侧，且离支承位置较近，高转速下陀螺效应的影响比质量增加的影响更加明显，因此临界转速反而增大。

3 稳定性计算分析

在液体火箭发动机涡轮泵中，最典型的失稳现象是转子出现次同步振动。这种次同步振动失稳在严重时可能导致支承轴承的失效，进而引起其他结构的严重破坏。由于转子的稳定性与转子结构形式、支承结构特性、流体作用力、安装配合工艺等一系列复杂因素有关，而且很多因素对稳定性的作用是非线性的，因此难以从理论上精确预测失稳转速。在实践中通常的做法是采取措施提高转子的稳定性裕度，即增大对数衰减率()

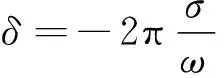
(6)

式中和分别是复频率=+i的实部和虚部。

关于对数衰减率的控制，不同的旋转机械设备研试厂家有不同的标准。根据文献[21]中的统计，其中要求最低的是在工作转速±10%范围内的临界转速对数衰减率都应大于0.1。根据SSME高压氢涡轮泵解决次同步振动的经验：转子的对数衰减率为0.14时，虽然可以使失稳转速增加至50 000 r/min以上，远高于工作转速34 700 r/min，但热试车中仍然有一定概率出现次同步振动问题；将对数衰减率控制在0.22以上才能保障转子的稳定性。

3.1 弹支处外阻尼为零

对25 tf发动机氢涡轮泵转子，考虑流体密封的附加刚度及阻尼作用，假设弹性支承处的外阻尼为0的情况下，计算得到的转子前两阶对数衰减率如图7所示。从图中可以看出，在转速0～100 000 r/min之间，一、二阶对数衰减率随着转速升高而增大，但最大值低于0.04，不满足上述对数衰减率应大于0.1的最低要求。因此，图1所示转子设计方案中，在弹性支承处设置金属橡胶阻尼器以增加转子系统外阻尼是十分必要的。

图7 外阻尼为0时转子对数衰减率随转速的变化Fig.7 Variation of logarithmic decrement with rotational speed when external damping is zero

3.2 金属橡胶阻尼器的作用

图1所示25 tf发动机氢涡轮泵转子支承方案中设置的金属橡胶阻尼器，可以为转子系统提供一定的外阻尼作用，能提高转子稳定性。根据文献[22]的研究，金属橡胶阻尼器的阻尼系数随着激励频率(转速)的升高而逐渐下降。本文以文献[22]的试验测量结果为参考，拟合得到金属橡胶阻尼器的阻尼系数随转速的变化规律，然后将拟合结果耦合到转子动力学计算程序，考虑阻尼系数随转速的变化，计算得到的转子前两阶对数衰减率如图8所示。

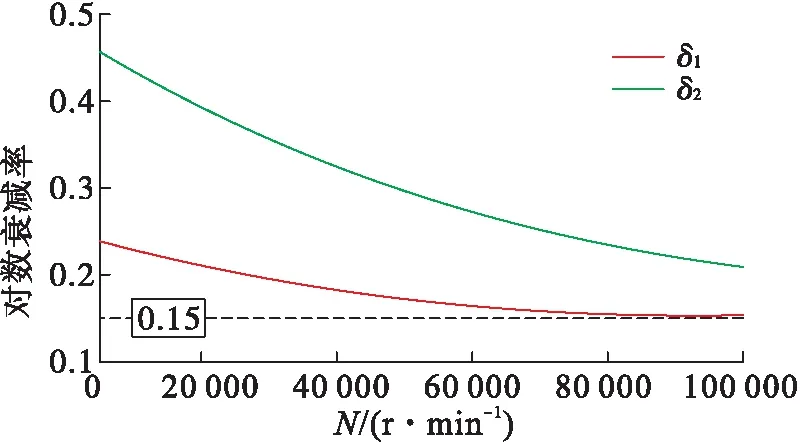
图8 增加金属橡胶阻尼器后转子对数衰减率随转速的变化Fig.8 Variation of logarithmic decrement with rotational speed when damper is added

从图8可以看出：考虑在弹性支承处设置的金属橡胶阻尼器的阻尼作用后，转子的前两阶对数衰减率相比图7无外阻尼时明显增大；由于金属橡胶阻尼器的阻尼系数随着转速升高而逐渐下降，前两阶对数衰减率都逐渐降低；在0～100 000 r/min之间，一阶对数衰减率逐渐降低至最小值0.15左右。

根据以上计算，现有的25 tf氢涡轮泵转子系统设计方案可将对数衰减率控制在0.15以上，满足通常的旋转机械对数衰减率应大于0.1的最低要求。但从上述SSME高压氢涡轮泵的研究和试验经验看，将对数衰减率提高到0.22以上转子的稳定性裕度更充足。

3.3 级间密封改进

表2中节点13对应的是级间密封，相应的附加刚度及阻尼系数是采用齿型密封结构的计算结果。根据相关研究，孔型结构密封可提供的流体阻尼作用要远大于齿型结构密封，因此，研究了级间密封由齿型结构改为孔型结构对转子稳定性的影响。

通过流场仿真计算得到的改进后的孔型级间密封可提供的附加刚度及阻尼与改进前的对比如表4所示。将表4所列的齿型、孔型级间密封的刚度及阻尼系数分别代入转子动力学计算程序，计算得到的级间密封改进前、后转子前两阶对数衰减率如图9所示。

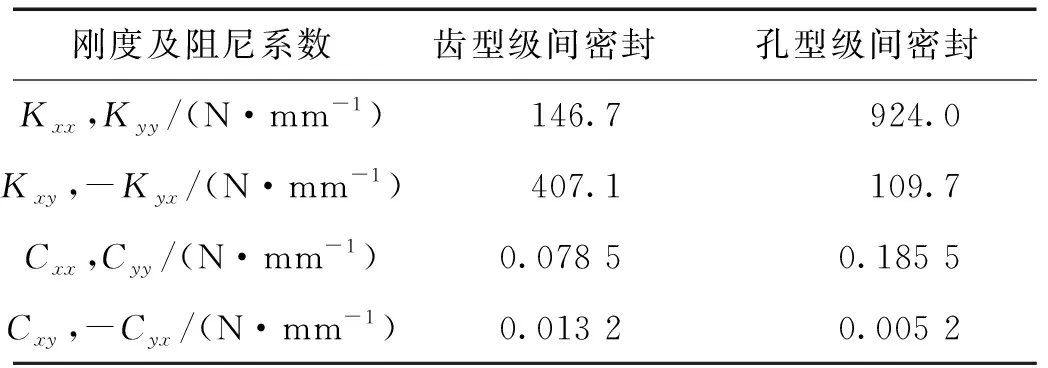
表4 级间密封改进前后刚度及阻尼系数对比Tab.4 Comparison of stiffness and damping between before and after seal improvement

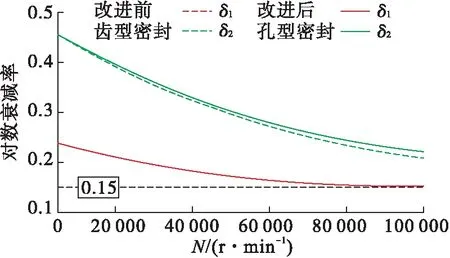
图9 级间密封改进前后转子对数衰减率对比Fig.9 Comparison of rotor logarithmic decrement between before and after seal improvement

从表4可知，将级间密封由齿型结构改为孔型结构后，密封流体对转子的直接刚度(、)和直接阻尼(、)显著增大，交叉刚度(、)则明显减小。这说明级间密封结构改进后，密封间隙内流体的周向流动明显削弱，对提高转子的稳定性有利。

从图9所示改进前、后转子对数衰减率对比来看，改进后的转子二阶对数衰减率相比改进前略有增大，而一阶对数衰减率基本没有变化。这说明级间密封改为孔型结构后，虽然密封流体对转子的阻尼系数显著增大，但对转子稳定性的改善不明显。根据图4所示转子振型分析，主要原因是级间密封位于转子一阶振型的节点(位移零点)附近，转子在此处的振幅很小，接近为0，级间密封的流体阻尼无法有效发挥作用，也就无法显著提高转子稳定性。

根据图4，转子的一阶模态振型是刚体摆动振型。因此，要提高转子的一阶对数衰减率，将位于转子两侧悬臂段的离心轮Ⅰ、涡轮盘Ⅰ和Ⅱ附近的流体密封改为阻尼更大的孔型结构效果最好。

4 结论

本文对25 tf发动机超高转速氢涡轮泵转子的动特性展开研究，采用有限元法建立转子动力学模型，考虑支承结构参振、密封流体的刚度及阻尼、支承刚度及阻尼随转速变化等因素的影响，计算分析了转子的临界转速、稳定性等动态特性，得出以下结论：

1)转子系统设计方案能够满足“临界转速与工作转速间隔裕度大于20%，转子弯曲应变能比例低于25%”的设计准则和目标要求。

2)转子二阶临界转速对泵端支承刚度变化更敏感，一、三阶临界转速对涡轮端刚度变化更敏感，适当降低泵端支承刚度，可以增强金属橡胶阻尼器对转子稳定性的作用效果，还能增大转子二、三阶临界转速间隔，增大转速可调范围。

3)流体密封附加刚度对转子前三阶临界转速的影响小于1%，在转子临界转速优化设计时可不考虑密封附加刚度的影响。

4)现有设计方案下转子一阶对数衰减率最小值约为0.15，满足通常转子稳定性设计准则最低要求，但裕度偏小，可采取措施将对数衰减率提高至0.22以上。

5)级间密封由齿型结构改为孔型结构可以显著增大流体阻尼系数，但对提高转子一阶对数衰减率作用不明显；根据转子振型，将悬臂段的离心轮Ⅰ、涡轮盘Ⅰ和Ⅱ附近的流体密封改为阻尼更大的孔型结构，对提高一阶对数衰减率效果更好。