重型发动机S型波纹管承压与变形补偿结构参数敏感特性

赵 剑，谭永华，陈建华，高玉闪

(1. 西安航天动力研究所，陕西 西安 710100； 2. 航天推进技术研究院，陕西 西安 710100)

0 引言

我国500 tf级重型液氧煤油发动机(简称发动机)将采用“泵后摇摆”的总体布局，即在涡轮出口与推力室入口之间设置柔性摇摆环节，仅摆动推力室控制推力矢量和调节火箭飞行姿态。采用“泵后摇摆”总体布局能有效减轻发动机质量、减小摇摆空间、降低摇摆力矩以及避免质心偏斜等，且发动机更紧凑、火箭构型更优，但是难点在于研制适用于高温、高压、富氧燃气的柔性摇摆组件。

柔性S形波纹管是摇摆组件的核心补偿元件，为多层薄壁柔性金属壳体。工程上对于金属波纹管的应用和研究多见于U形波纹管。作为柔性补偿元件，波纹管的变形补偿能力是重要的性能指标，其中包括轴向变形、弯曲变形以及扭转变形的补偿。对于同等变形补偿要求，采用等厚度的多层波纹管，可以有效降低变形补偿时的应力水平和刚度，因而多层波纹管得到广泛应用和研究。在内压和位移共同作用下，波纹管易发生失稳失效，常见的有柱失稳和面失稳，故应针对使用环境，结合不同波纹管抗失稳性能合理选择波纹管结构。由于S形波纹管结构和加工工艺复杂，受制于应用规模和市场需求，工程上对S形波纹管的应用和研究相对较少。但是S形波纹管具有独特的结构性能，非常契合泵后摆发动机的应用需求。

本文以一种新型S形波纹管为研究对象，提出了一种基于正交试验设计理论和非线性有限元方法的结构参数敏感特性的分析方法。该方法通过参数化的正交仿真试验，基于相关性分析、方差分析和单因子响应分析等方法，获得了不同结构参数对结构特性的影响程度和作用模式，研究结果可供工程应用参考。

1 S形波纹管几何结构

相对于U形和C形波纹管，S形波纹管波形相对复杂，其波形的明确定义较为少见。这里定义S形波形为3段圆弧相切式结构，如图1所示，为波高，为波距，为波谷半径，为波峰半径，为过渡圆弧半径。

图1 三段圆弧波形结构Fig.1 The shape of 3 tangential arcs

图2为S形波纹管结构示意图，其中为波纹管外径，为波纹管内径。

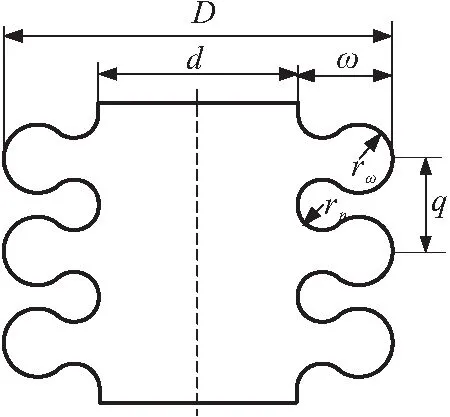
图2 S形波纹管结构示意图Fig.2 Schematic diagram of S-shaped bellows

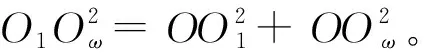
(1)

几何参数、、、、和必须满足两个约束，即数学和物理约束，故其中仅有4个几何参数可独立取值。由于波峰和波谷半径差异较小，且假定和相等，可将S形波形几何参数简化为3个独立影响因子。综合考虑其结构参数，得到6个独立的S形波纹管影响因变量，即、、()、、和。

2 研究思路与方法

给定影响因子的分布范围如表1所示，大量计算检验表明，影响因子在表1范围内的任意组合，都可以形成符合数学和物理要求的S形波纹管结构，表明在表1范围内影响因子相互独立。

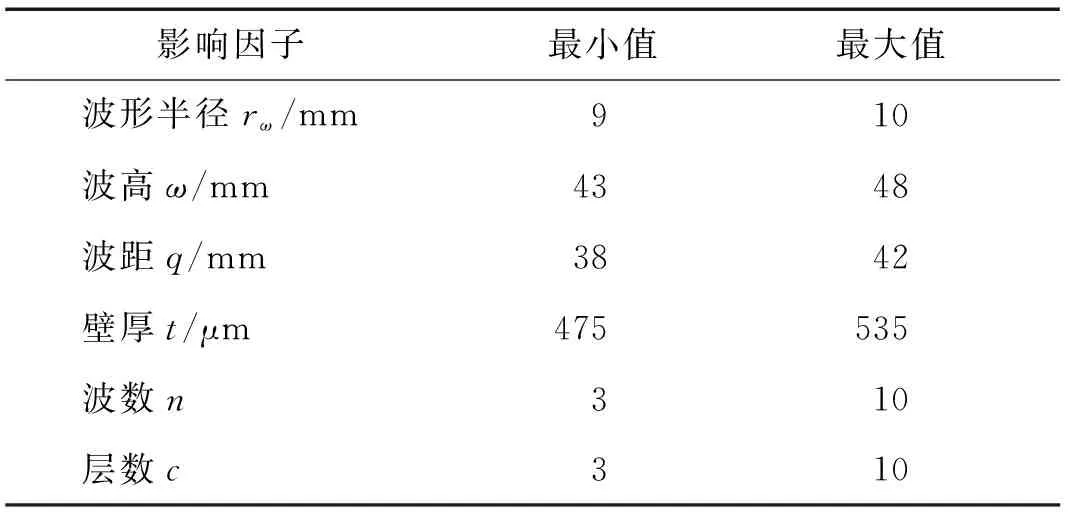
表1 影响因子分布Tab.1 The distribution of structural parameters

S形波纹管结构由以上6类影响因子决定，不同影响因子组合形成的波纹管，其结构特性如刚度、强度以及稳定性等都有差异。为了合理有效地评估各影响因子对波纹管结构特性的影响规律、识别出参数敏感度关系，需要进行大样本计算。假定每个影响因子选择8种水平，则有8=262 144种组合，若全面分析，将耗费大量的计算和存储成本；如果选择任意数量的组合分析，可能得不到准确的结果。因此，引入正交试验设计方法，平衡计算成本与精度，并基于概率统计理论对计算结果进行分析和处理。

参数敏感度分析流程由4个模块组成(见图3)。方案设计模块基于表1中影响因子的均匀分布，设计正交试验方案。仿真组织模块以OPTIMUS为控制平台，通过数据通信读入正交试验方案、调用仿真软件分析以及提取目标响应，使整个分析流程自动化。仿真计算模块基于ANSYS参数化编程语言APDL形成S形波纹管的参数化仿真程序，将建模、网格处理、加载以及求解等步骤参数化处理，极大地节省时间和精力。数据处理模块基于相关性分析、主成分分析及方差分析研究影响因子与响应之间的参数敏感度信息，总结影响规律。

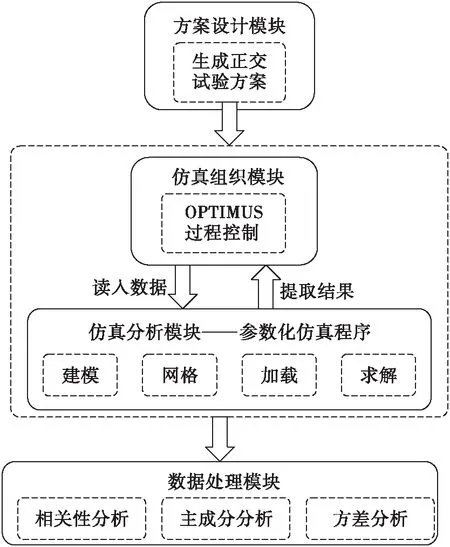
图3 参数敏感度分析流程Fig.3 Flowchart of the sensitivity analysis method

3 非线性有限元分析及验证

3.1 模型轴对称等效

对于承受内压和轴向位移载荷的波纹管，其自身结构、载荷以及变形都呈现轴对称特征，因而可采用二维轴对称模型进行分析。波纹管材料为1Cr18Ni9Ti，弹性模量=2.06×10MPa，泊松比=0.3，屈服强度=205 MPa。

根据材料的性质，采用Mises流动理论描述材料进入塑性阶段的本构关系，在Drucker公设和Ilyushin假设前提下，塑性变形满足正交法则，屈服条件为

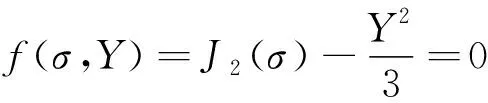
(2)

式中：为应力张量；()是应力张量第二不变量；是强化参数。引入Mises等效应力表征应力状态，即

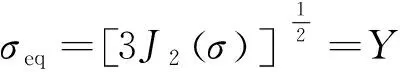
(3)

式中为von Mises等效应力。

3.2 单元与网格收敛性分析

波纹管变形补偿原理与弹簧类似，但对于多层波纹管而言，由于层间接触作用，其应力和刚度响应都呈现非线性，属于非线性有限元分析范畴。有限元模型选用轴对称SHELL209单元，该单元为3节点非线性壳单元，适合线性、大转动和大应变非线性分析。

网格密度对计算结果的影响很大，网格数较少时，可能导致分析结果连续性差，结果失真；网格数目太多，计算成本太高。为此，分析了内压载荷下，网格尺寸在1～3.5 mm之间均匀分布时S形波纹管位移随网格尺寸的变化关系。如图4所示，其中最大应力和变形变化范围小于1%，网格尺寸满足网格收敛性要求。

图4 最大变形随网格尺寸变化Fig.4 Variation of maximum deformations to mesh sizes

3.3 算法验证

为了验证模型轴对称等效、单元以及网格处理的可行性和有效性，参考文献[2-3]中内径为508 mm的多层波纹管轴向刚度试验结果及EJMA标准的计算结果进行验证。验证内容为4层U形波纹管的刚度分析，仿真中需要考虑多层波纹管的材料、几何和接触非线性特征，仿真得到的刚度值为最小二乘拟合结果。

从表2可知，3种方法得到的刚度值较为接近，有限元解与试验值的最大偏差为6.63%，有限元解与EJMA解的最大偏差为2.42%，满足EJMA标准建议的精度要求，证实了模型和分析方法可行。

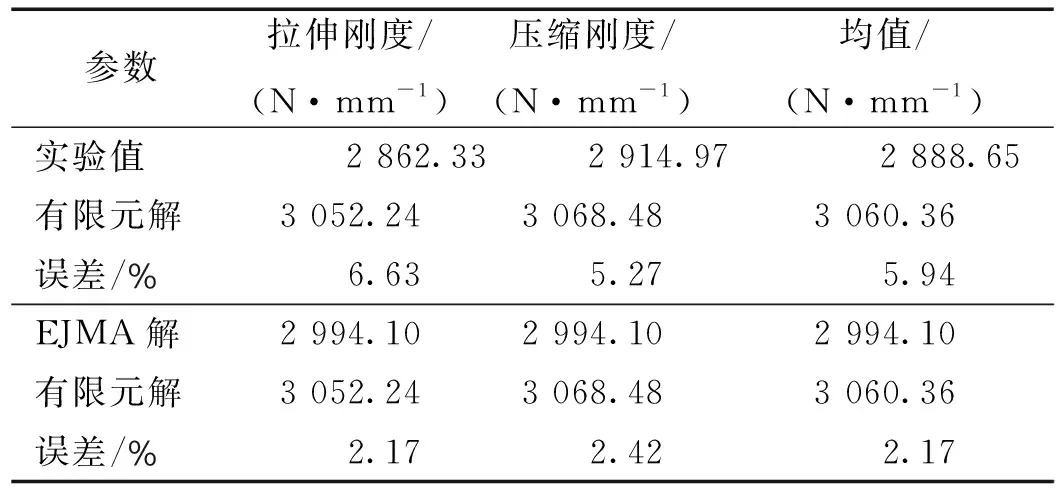
表2 轴向刚度分布Tab.2 The distribution of axial stiffness

4 敏感度分析方法

4.1 相关性分析

相关性是指多变量数据之间存在着某种内在关联，主要有正相关[见图5(a)]和负相关[见图5(b)]两类。

图5 相关性分布示意图Fig.5 Schematic diagrams of correlativity distribution

一般采用积距相关系数来衡量变量之间相关性强度，即

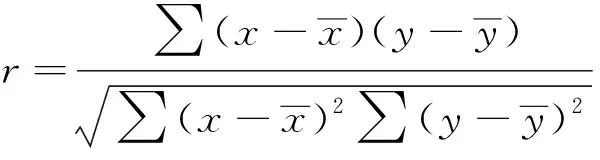
(4)

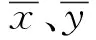
选择表1中影响因子均匀分布的8种水平，形成正交试验方案。表3表明影响因子的互相关系数为0，反映出影响因子之间相互独立。

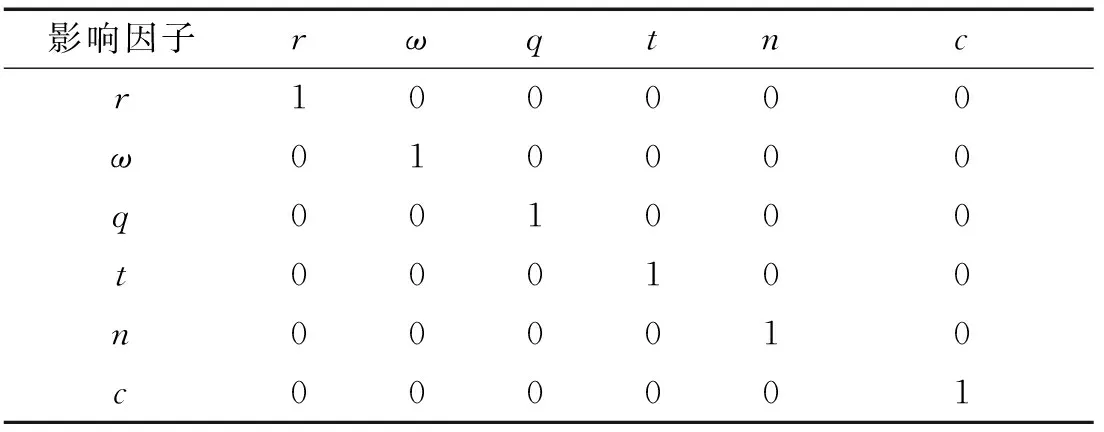
表3 影响因子相关系数Tab.3 The correlation coefficients of factors

4.2 主成分分析

主成分分析是在尽量保留数据信息的原则下，对高维变量空间进行降维处理，即使用指标体系的少数几个线性组合构成综合指标，并尽可能多地保留原指标信息，这些综合指标就称为主成分。

设有个指标=(，，…，)，若用第一主成分来取代原维变量，应该取保留数据信息量最多的一个方向，即方差最大的方向(见图6)。

图6 主成分分布示意图Fig.6 Schematic diagrams of principal component analysis

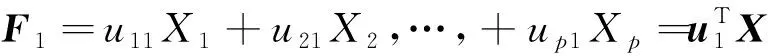
(5)

式中为维正交向量。

若需要考虑第二主成分，即寻找与垂直的方向，依次类推，便可以得到一个维的主超平面，，…，(≤),它是原维空间所有线性变换空间中保留数据信息最大的维子空间，即

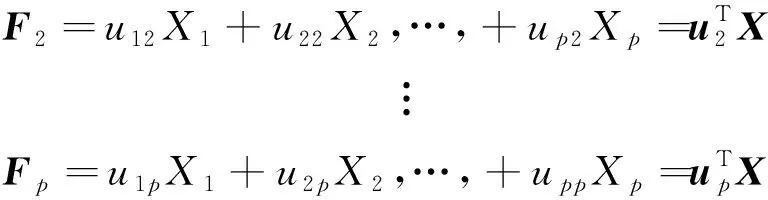
(6)

式中=(，，…， )为正交矩阵。

设的协方差矩阵为，满足

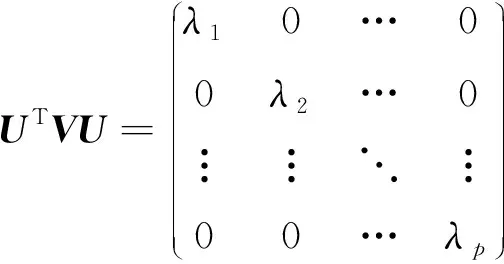
(7)

式中,,…，为的特征根。

在实际应用中，中各个分量的意义不同，量纲也不同，从而影响协方差阵的特征根与特征向量计算，为了消除这种不利影响，通常将变量标准化,即

(8)

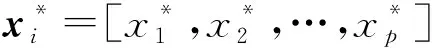
4.3 主成分分析

方差分析可以判断影响因子是否对响应有显著影响，从而得到各影响因子敏感度的量化指标。方差分析中，所关心的试验结果称为指标，对指标产生影响的因素称为因子，因子所处的状态称为水平。

设某个试验指标分别受和两个因子影响，其中因子有个水平，，…，，因子有个水平，，…，，这样共有·个不同水平的组合。引入下列符号

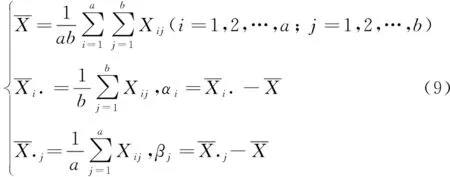
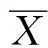
0：==…==0

(10)

同样，分析的不同水平对试验指标是否有显著影响，相当于检验如下假设

0：==…==0

(11)

从而建立方差分析模型

(12)

引入下述各变差平方和

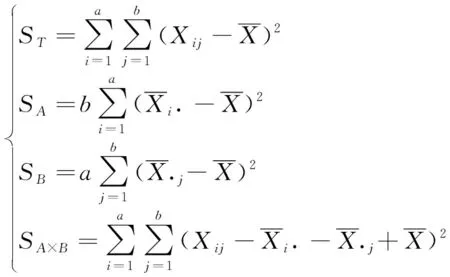
(13)

式中：为变差平方和；和分别反映因子和对试验指标的影响；×主要反映随机误差的波动。通过比较和的大小，得到和的影响程度高低。

5 结果与分析

5.1 内压载荷响应敏感度分析

S形波纹管两端固支，在内壁面均匀施加0.5 MPa内压，考虑von Mises应力极值、周向应力极值、子午向应力极值以及总位移极值共4类响应指标，其中某一种参数组合波形应力云图如图7所示。

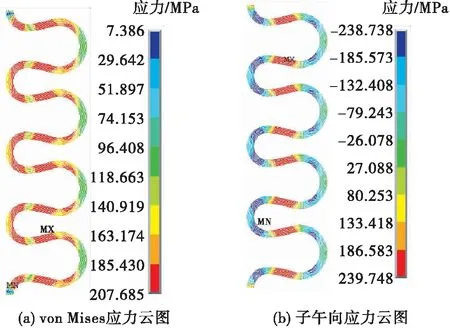
图7 一种参数组合波形应力云图Fig.7 The von Mises stress of one combined bellows

5.1.1 相关性分析

从表4中可以发现，各响应之间的秩相关系数绝对值大于0.94，表明各响应指标之间相关程度很高，可以用少量的响应指标表征所有响应指标的效应。该结论符合有限元计算的基本原理，即应力指标通过变形演化而来，求解得到了位移场，也就知道了应力场。

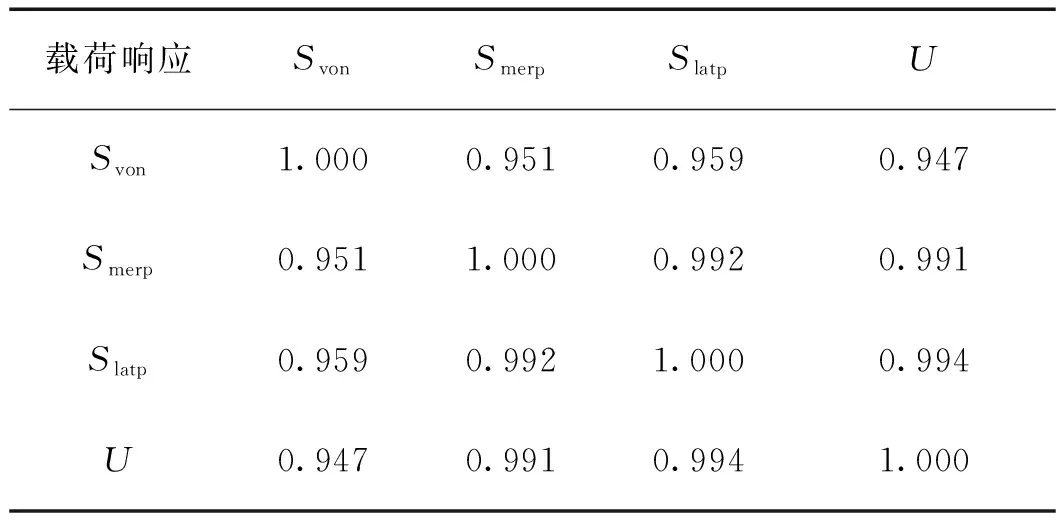
表4 内压载荷响应相关系数Tab.4 The correlation coefficients of pressure responses

5.1.2 主成分分析

将各响应数据标准化，并进行主成分分析，得到各特征值如表5所示。

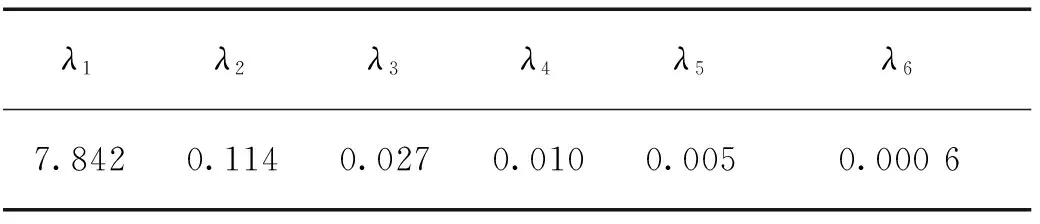
表5 内压响应标准化协方差矩阵特征值Tab.5 The eigenvalues of normalized covariance matrix of pressure responses

从表5可知，特征值的贡献率为98.3%，故可以用第1主成分表征整体响应的综合效应。

5.1.3 方差分析

对于显著水平=0.05，比较表6中列数据与临界值(7，21)=2.49可得：在多层波纹管总厚度一定时，对于内压载荷响应，S形波纹管影响因子的影响程度从高到低为层数>波高>单层厚度>波数>半径>波距，其中，层数影响最显著，半径和波距的影响可以忽略。

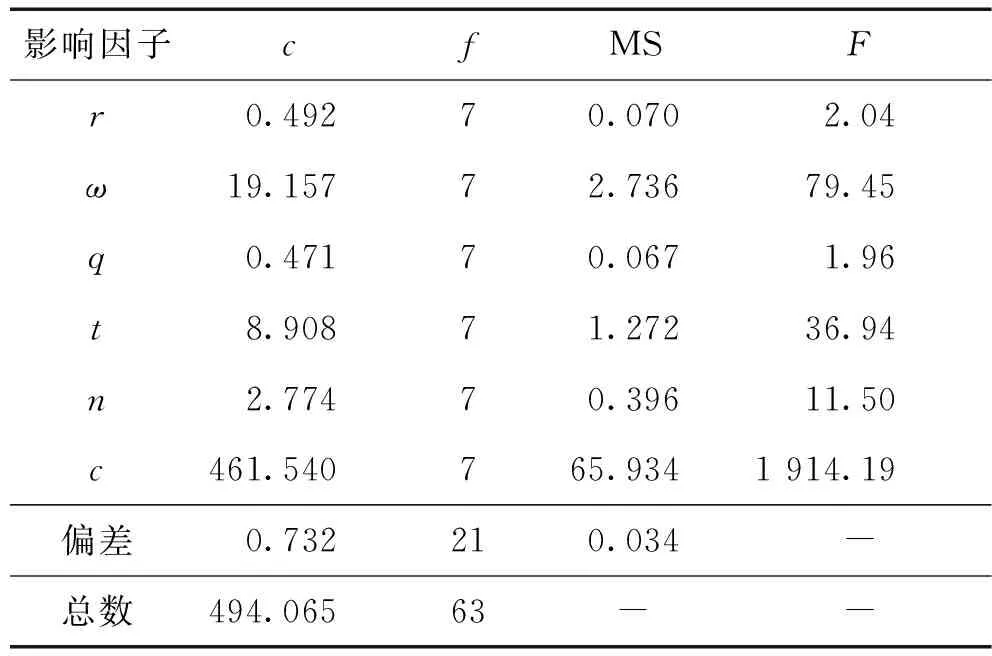
表6 载荷方差分析Tab.6 Load analysis of vaniance

5.1.4 单因子响应分析

选定表1中各影响因子取值范围的中间值作为基准波形，单独研究各影响因子在其取值范围内在内压载荷下von Mises应力极值的影响规律。为了便于比较，将各影响因子和von Mises应力分别无量纲化处理，获得图8所示的单因子影响关系。

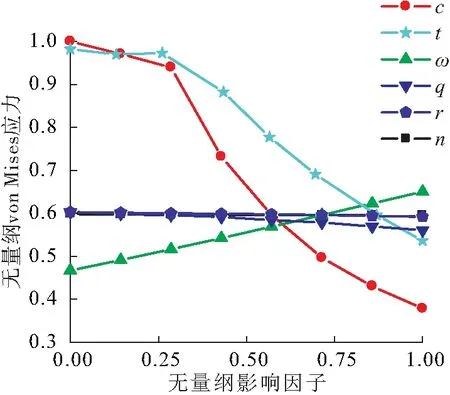
图8 无量纲影响因子对无量纲von Mises应力的影响Fig.8 The distributions of normalized von Mises stress to different normalized parameters

对于内压载荷，管壁厚度是最重要的承压性能指标，故增加层数和单层厚度，能有效增大承压能力，降低应力水平。波高越大，波峰波谷过渡圆弧长度越大，内压沿过渡圆弧长度产生的压力变形和应力就越大。波数、半径以及波距增大，应力略有下降，从图8中可以发现，这三者的影响程度远不如其他参数重要。

5.2 轴向位移响应敏感度分析

S形波纹管一端固支，另一端施加10 mm轴向位移，考虑von Mises应力极值、周向应力极值、子午向应力极值和轴向刚度共4类响应指标，并分别处理应力指标与轴向刚度指标数据，其中某一种参数组合波形von Mises应力云图如图9所示。

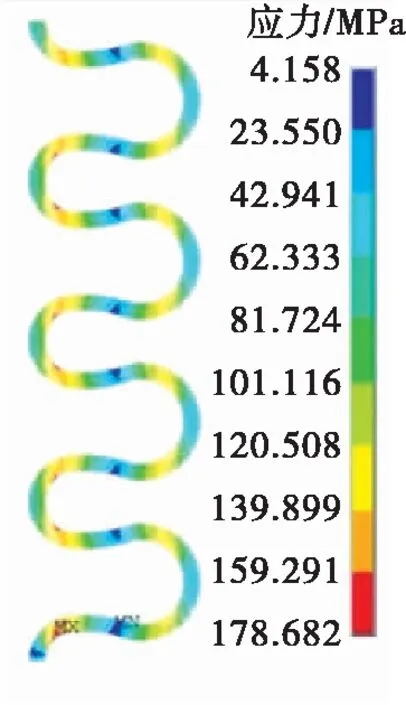
图9 一种组合波形von Mises应力云图Fig.9 The von Mises stress of one combined bellows

5.2.1 相关性分析

表7反映出在轴向位移载荷作用下，各应力响应之间的相关程度大于0.87，因此，可以用较少的响应指标反映所有响应的影响规律。

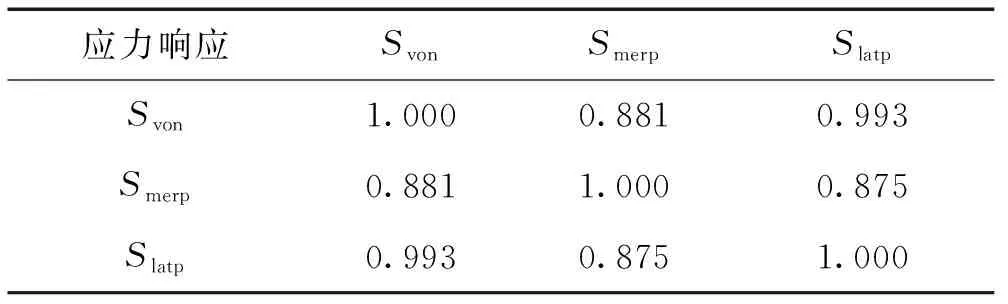
表7 应力响应相关系数Tab.7 The correlation coefficients of stress

5.2.2 主成分分析

将应力响应指标标准化，并进行主成分分析，得到各特征值如表8所示。

表8 应力响应标准化协方差矩阵特征值Tab.8 The eigenvalues of normalized covariance stress

特征值的贡献率为98.03%，故可以用第1主成分表征整体响应的综合效应。

5.2.3 位移应力响应方差分析

对于显著水平=0.05，比较表9中列数据与(7，21)=2.49可得：对于轴向位移应力响应，S形波纹管影响因子的影响程度关系由高到低依次为波数>层数>半径>波高>单层厚度>波距，其中波数和层数影响最大，波距的影响可以忽略。

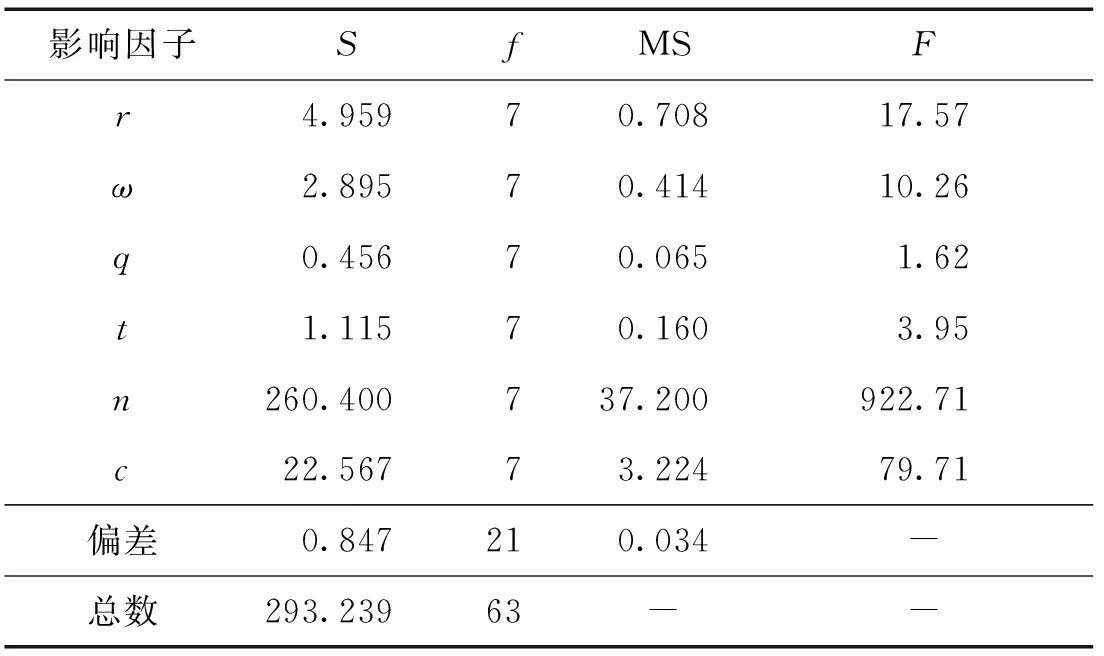
表9 应力方差分析Tab.9 Stress analysis of vaniance

同理，比较表10中列数据与(7，21)=2.49的关系可得：对于轴向位移刚度响应，S形波纹管6个影响因子的影响程度关系从高到低依次为层数>波数>半径>单层厚度>波距>波高，其中波数与层数影响最大，单层厚度、波距和波高的影响可以忽略。

表10 轴向刚度方差分析Tab.10 Axial stiffness analysis of vaniance

5.2.4 单因子响应分析

选定表1中各影响因子取值范围的中间值作为基准波形，单独研究各影响因子在其取值范围内对位移载荷下von Mises应力极值和刚度的影响规律。为了便于比较，将各影响因子和载荷响应分别无量纲化，获得图10和图11所示的单因子影响关系。

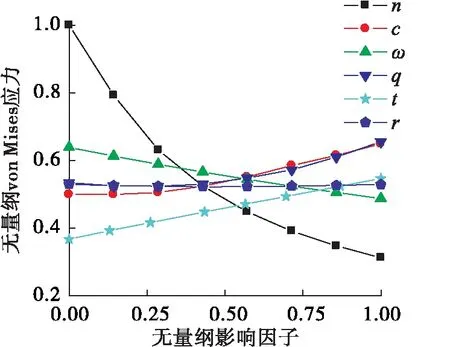
图10 无量纲影响因子对无量纲von Mises应力的影响Fig.10 The distribution of normalized von Mises stress to normalized parameters

图11 无量纲影响因子对无量纲轴向刚度的影响Fig.11 The distribution of normalized axial stiffness to normalized parameters

从图10和图11中可知，波数增加，波纹管长度增大，在同等位移作用下，单个波纹的变形减小，故应力水平和刚度降低，应力极值、刚度与波数呈现双曲函数关系。单层厚度和层数增加使得总壁厚增大，波形最小曲率减小，波纹管轴向截面积增大，应力极值与刚度都增大。波高增加，过渡圆弧长度增大，刚度减小，应力也减小。波距增大时，应力极值先减小后增大，存在应力极小值点，半径对应力极值和刚度的影响最小。

6 结论

为了获得重型发动机泵后摇摆S型波纹管组件的结构敏感特性，为工程设计与应用提供支持,本文针对新型S形金属波纹管，定义了3段圆弧相切的S形波形，将其结构参数简化为6个影响因子，提出了一种基于正交试验设计、非线性有限元方法以及数理统计理论的结构参数敏感特性研究方法，并研究获得了其参数敏感特性，主要结论如下：

1)对于承压特性，在多层波纹管总厚度一定时，波纹管承压能力对影响因子的敏感度关系为：层数>波高>单层厚度>波数>半径>波距，其中单层厚度和层数决定了波纹管的总壁厚，因此影响显著，波距和波高的影响可以忽略。

2) 对于位移补偿特性，影响因子对波纹管轴向位移应力响应敏感度关系为：波数>层数>半径>波高>单层厚度>波距，而影响因子对波纹管轴向刚度的敏感度关系为：层数>波数>半径>单层厚度>波距>波高。波数与层数的影响最为显著，其中波数增加，波纹管长度增大，在同等位移作用下变形减小，刚度与应力极值呈现双曲函数减小；层数增加，刚度显著增大，应力极值增大。波距和波高的影响较小。